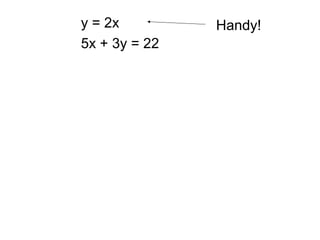Intersection of lines
- 1. Block 1 Intersection of Lines
- 2. What is to be learned? • How to find where straight lines meet (point of intersection)
- 3. 3x + 2y = 17 2x – 5y = 5 3x + 2y = 17 X5→ 15x + 10y = 85 2x – 5y = 5 X2→ 4x – 10y = 10 Add 19x = 95 x = 5 Consider two lines simultaneous equations 15 + 2y = 17 y = 1 POI (5 , 1) (the Elimination Method)
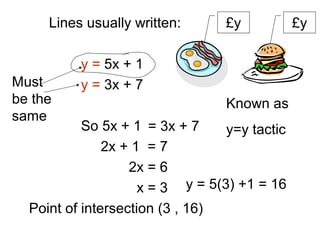
- 4. Lines usually written: y = 5x + 1 y = 3x + 7 Could still use elimination! → y – 5x = 1 → y – 3x = 7
- 5. Lines usually written: y = 5x + 1 y = 3x + 7 So 5x + 1 2x + 1 = 7 2x = 6 x = 3 Point of intersection (3 , 16) Must be the same y = 5(3) +1 = 16 Known as y=y tactic= 3x + 7 £y £y
- 6. Using y = y Find the points of intersection, for these pairs of lines: 1. y = 5x – 3 and y = 2x + 12 2. y = 7x + 8 and y = x +20 3. y = -2x + 8 and y = 2x + 12 4. y = 5x + 3 and y = 24 – 2x (5,22) (2,22) (-1,10) (3,18)
- 7. What is to be learned? • How to find where straight lines meet (point of intersection)
- 8. y = 2x 5x + 3y = 22 Handy!
- 9. y = 2x 5x + 3y = 22 Replace y with 2x 5x + 3 = 22 5x + 6x = 22 11x = 22 x = 2 x = 2 y = 2(2) = 4 Intersection (2 , 4) (2x)y Handy! substitution
- 10. y = 4x + 3 3x + 2y = 17 substitution
- 11. y = 4x + 3 3x + 2y = 17 Replace y with 4x + 3 3x + 2 = 17 3x + 8x + 6 = 17 11x + 6 = 17 11x = 11 x = 1 y = 4 (1) +3 = 7 Intersection (1 , 7) (4x+3)y substitution
- 12. Using Substitution Find intersections of these lines: 1. x = 8 and 2y + 4x = 42 2. y = 8 and 3y = 2x + 4 3. y = 2x and 2y + 3x = 28
- 13. Using Substitution Find intersections of these lines: 1. x = 8 and 2y + 4x = 42 (8 , 5) 2. y = 8 and 3y = 2x + 4 3. y = 2x and 2y + 3x = 28
- 14. Using Substitution Find intersections of these lines: 1. x = 8 and 2y + 4x = 42 (8 , 5) 2. y = 8 and 3y = 2x + 4 (10 , 8) 3. y = 2x and 2y + 3x = 28
- 15. Using Substitution Find intersections of these lines: 1. x = 8 and 2y + 4x = 42 (8 , 5) 2. y = 8 and 3y = 2x + 4 (10 , 8) 3. y = 2x and 2y + 3x = 28 (4 , 8)
- 16. Points of Intersection Can use • Simultaneous Equations • y = y • Substitution Depends on way lines are given
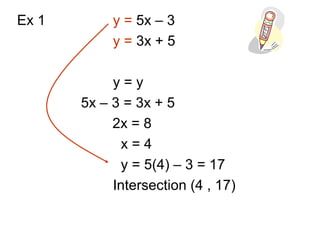
- 17. Ex 1 y = 5x – 3 y = 3x + 5
- 18. Ex 1 y = 5x – 3 y = 3x + 5 y = y 5x – 3 = 3x + 5 2x = 8 x = 4 y = 5(4) – 3 = 17 Intersection (4 , 17)
- 19. Ex 2 3x + 2y = 15 2x + 5y = 21 Simultaneous Equations
- 20. Ex 3 2x + 3y = 13 y = 2x – 1 Substitute y= 2x – 1 into* 2x + 3(2x – 1) = 13 2x + 6x – 3 = 13 8x = 16 x = 2 y = 2 (2) – 1 = 3 (from second equation) Intersection (2 , 3) *
- 21. . You can often rearrange the equations to use your favourite tactic