Ml lesson 4 7
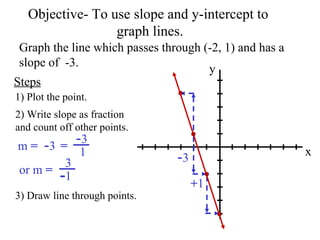
- 1. Objective- To use slope and y-intercept to graph lines. Graph the line which passes through (-2, 1) and has a slope of -3. x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = - 3 = - 3 1 - 3 + 1 or m = 3 - 1 3) Draw line through points.
- 2. Graph the line which passes through (3, 2) and has a slope of . x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = 3 4 + 3 + 4 or m = - 3 - 4 3) Draw line through points. 3 4
- 3. Graph the line which passes through (-5, 4) and has a slope of . x y 1) Plot the point. Steps 2) Write slope as fraction and count off other points. m = - 3 2 - 3 + 2 3) Draw line through points. - 3 2
- 4. Slope-Intercept Form of the Linear Equation Any linear equation which is solved for y is in slope-intercept form. y = mx + b Find the slope and y-intercept of the following linear equations: 1) y = 3x + 4 2) y = - 2x - 1 3) y = 5x 4) y = x - 4 5 8 5) y = x - - 2 9 1 4 6) y = 6 m = 3 b = 4 m = - 2 b = - 1 m = 5 b = 0 m = b = - 4 5 8 m = b = - 2 9 - 1 4 m = 0 b = 6
- 5. Slope-Intercept Form of the Linear Equation Write a linear equation in the form y = mx + b given the following. 1) m = 2, b = -3 2) m = , b = 5 3) m = , y-int. = 2 4) m = 0, b = 6 5) m = , b = 0 6) m = 1, b = y = 2x - 3 y = 6
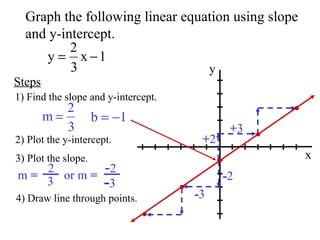
- 6. - 3 Graph the following linear equation using slope and y-intercept. x y 1) Find the slope and y-intercept. Steps 2) Plot the y-intercept. m = 2 3 or m = - 2 4) Draw line through points. 3) Plot the slope. + 2 + 3 - 2 - 3
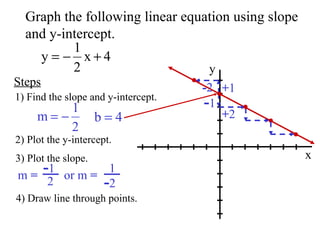
- 7. - 1 - 2 Graph the following linear equation using slope and y-intercept. x y 1) Find the slope and y-intercept. Steps 2) Plot the y-intercept. m = - 1 2 or m = 1 4) Draw line through points. 3) Plot the slope. + 2 + 1 - 2
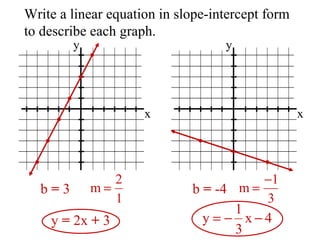
- 8. Write a linear equation in slope-intercept form to describe each graph. x y x y b = 3 y = 2x + 3 b = -4
- 9. Write a linear equation to describe this situation and graph. Kyle has $300 and is saving $25 a week. Let x = # of weeks Let y = savings in dollars y = 25x + 300 change start value y = mx + b Slope Y-intercept Savings Weeks 500 400 300 200 100 0 0 1 2 3 4 5 m = $ 25 / week b = 300
- 10. Pam received $100 and spends $4 each week. 1) Write an equation for the money, y, she has after x weeks. 2) What are the slope and y-intercept? y = 100 - 4x m = - 4 b = 100
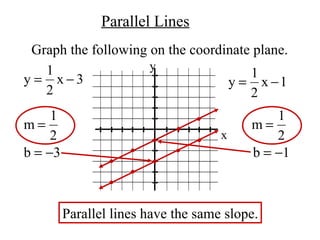
- 11. Parallel Lines Graph the following on the coordinate plane. x y Parallel lines have the same slope.
- 12. Tell whether the lines below are parallel. 1) 3x + y = 7 y = -3x + 1 -3x -3x y = -3x + 7 m = -3 y = mx + b m = -3 Lines are parallel! Same slope!