Lesson 14 centroid of volume
- 1. TOPIC APPLICATIONS CENTROIDS OF SOLIDS OF REVOLUTION
- 2. CENTER OF GRAVITY OF A SOLID OF REVOLUTION The coordinates of the centre of gravity of a solid of revolution are obtained by taking the moment of an elementary disc about the coordinate axis and then summing over all such discs. Each sum is then approximately equal to the moment of the total volume taken as acting at the centre of gravity. Again, as the disc thickness approaches zero the sums become integrals.
- 3. THE MOMENT OF A SOLID of volume V, generated by revolving a plane area about a horizontal or vertical axis, with respect to the plane through the origin and perpendicular to the axis may be found as follows: 1.Sketch the region, showing a representative strip and the approximating rectangle. 2.Form the product of the volume, disc or shell generated by revolving the rectangle about the axis and the distance of the centroid of the rectangle from the plane, and sum for all the rectangles. 3.Assume the number of rectangles to be indefinitely increased and apply the fundamental theorem.
- 4. When the area is revolved about the x-axis, the centroid is on that axis. Which means that, for solids generated by revolving the plane area about an axis, its centroid is on that axis, thus, giving one coordinate. )z,y,x(C If Myz is the moment of the solid to the y-z plane through the origin and perpendicular to the x-axis, then xvMyz ⋅= xzMSimilarly if is the moment of the solid with respect to the x-z plane through the origin, and perpendicular to the y-axis, then is zero, considering that solids generated by revolving a plane area only about a horizontal or vertical axis, where which is the moment about an x-y plane, is always zero. ( ). z xyM 0=xyM yvMxz ⋅=
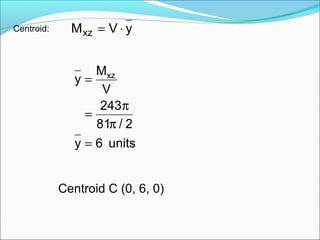
- 5. 1. Determine the centroid of the solid generated by revolving the area bounded by the curve y = x2 , y = 9, and x = 0, about the y-axis. Since the axis of revolution is the y-axis, the centroid of the solid is on that axis, giving . .0=x h= 9-y y = x2 y=y y = 9 ( 3 , 9 ) ( x , y ) ),,( zyxC • )0,6,0(C EXAMPLE ,
- 6. ∫∫ ⋅−⋅⋅π= dx)y(xdv 92 ( )∫ = = −⋅⋅ππ= 3x 0x dxy9x22V 2 xycesin = ( ) ( ) ( ) unitscu. 2 81 03 4 1 3 2 9 2 4 x 2 x 92 dxxx92 xdx)x9(2V 42 3 0 42 3 0 3 3 0 2 π = − −π= −⋅π= −π= −π= ∫ ∫ ydVdMxz ⋅= 2 9 y y + = ( ) ydxyxdMxz ⋅⋅−⋅⋅π= 92 ( )∫∫ ⋅ + ⋅−⋅⋅π= dx y yxdMxz 2 9 92 ( ) ( ) ( ) ( ) ( ) 243 03 6 1 3 2 81 6 x 2 x 81 dxxx81 xdxx81 xdxy81M 62 3 0 62 3 0 5 3 0 4 3 0 2 xz π= − −π= −⋅π= −π= −π= −π= ∫ ∫ ∫ Moment about the x-z plane:
- 8. xy 42 =42 −= xy .4=x 2. Find the coordinates of the centroid of the solid generated by revolving the area within and the line about EXAMPLE )0, 8 5 ,4(Canswer units.cuV 5 216π = π= 27xzM
- 9. EXERCISES: Determine the coordinates of the centroids of the solids generated by revolving: 1. the first quadrant region bounded by the curve y = 4 – x2 about the y –axis. 2. the third quadrant region bounded by the curve y = x3 and y = x about y – 1 = 0. 3. the region bounded by the curve y2 = 4x , the lines x = 0 and y = 4, about x + 1 = 0. 4. the region bounded by the curves y = x2 and y2 = – x about the line y+1 = 0. 5. the region bounded by the curves y = 6x – x2 and y = x2 – 2x about x – 4 = 0.
- 10. EXERCISES: Determine the coordinates of the centroids of the solids generated by revolving: 1. the first quadrant region bounded by the curve y = 4 – x2 about the y –axis. 2. the third quadrant region bounded by the curve y = x3 and y = x about y – 1 = 0. 3. the region bounded by the curve y2 = 4x , the lines x = 0 and y = 4, about x + 1 = 0. 4. the region bounded by the curves y = x2 and y2 = – x about the line y+1 = 0. 5. the region bounded by the curves y = 6x – x2 and y = x2 – 2x about x – 4 = 0.