Acceptance sampling

Introduction
• Quality control is an activity in which measures are taken
to control quality of future output.
• Sampling refers to observation of a population or lot for
the purpose of obtaining some information about it.
• Acceptance sampling is a quality control technique.

Acceptance sampling
• Acceptance sampling is defined as sampling inspection in
which decisions are made to accept or reject products or
services.
• It is a decision making tool by which a conclusion is reached
regarding the acceptability of lot.
• Statistical quality control technique, where a random sample is
taken from a lot, and upon the results of the sample taken the lot
will either be rejected or accepted.

Acceptance sampling
• Accept Lot- Ready for customers
• Reject Lot-Not suitable for customers
• Statistical Process Control(SPC)-Sample and determine if in
acceptable limits

Purpose:
• Determine the quality level of an incoming shipment or, at
the end production.
• Ensure that the quality level is within the level that has been
predetermined.

How is it done?
• BEP = cost of inspection per item / cost of later repair due to a
defective item
• P = estimated proportion of defectives in the lot.
• If P ≈ BEP, use acceptance sampling
• If P > BEP, use 100% inspection
• Problems with 100% inspection
• Very expensive
• When product must be destroyed to test
• Inspection must be very tedious so defective items do not slip
through inspection

When is it done?
• When products in use could be damaged easily
• When using new suppliers
• When new products produced
• When current supplier in question
• Testing whole lot could be harmful

Method:
Take sample
Inspect Sample
Decision
Reject LotAccept lot Sample again
Decision
Return lot to
supplier
100% inspection

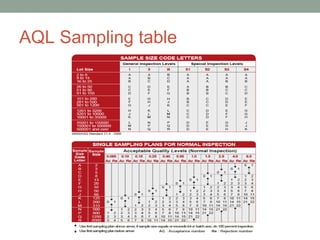
Creation of an acceptance sampling
plan:
Step 1: Determine your AQL
•Define a different AQL level for each defect type (minor, major
& critical).
• Inspect for each defect over the entire sample size and ensure an
acceptable rate for each defect type.
•In general, the following AQL’s are applied to Critical, Major &
Minor Defects:
•Critical – 0.1
•Major – 2.5
•Minor – 4.0

Step 2: Pick Your Risk Factors (α & β)
There are 2 types of risks:
•Consumer risk (β)
•Producer risk (α)
•Consumer Risk is the risk that your sampling plan will lead you
to accept a lot of product that does not actually meet your quality
standards.
•Producers Risk is the risk that a sampling plan may lead to the
rejection of a lot that actually does meet all quality standards.

Step 3: Know your data type
To choose the correct sampling plan, you must understand the
type of data you’re collecting.
Your data will either be Attribute or Variable.
3.1 – Sampling Plan Standard for Attribute Data:
Sampling Plans for attribute data are constructed such that you
will test a sample quantity(n) of product from the overall
population (N) and compare the number of non-conformances
you observe (d) against a predefined acceptance number (a) &
rejection number (r).

3.2 – Sampling Plan Standard for Variable Data:
• Sample sizes for variable data is much smaller than that of
attribute data.
•These Sampling plans assume that the data is distributed
Normally and rely on statistical calculations like the sample
Average, Standard Deviation or Range.

Step 4 – Determine Which Sampling Plan You
Want to Use
•In general, there are 4 different, predefined types of sampling
plans you can utilize.
•Each one will have a different sent of acceptance/rejection rules
and will also require a different number of samples to be tested.
The 4 different types of sampling plans are:
•Single Sampling Plan
•Double Sampling Plan
•Multiple Sampling Plan
•Continuous Sampling Plan

Single sampling plan
• A plan in which inspector is forced to make a decision
concerning acceptability of a lot or batch on the basis of
inspection of units in one sample taken from that lot.
• It can be described in terms of 3 constants.
• N,the lot size
• n,the sample size
• c,the acceptance number.c is the maximum allowable
defects in sample.
• If sample contains c or fewer defectives, lot will be
accepted & if it contains more than c lot will be
rejected.

Double sampling plan:
• These are characterized by two sample size along with two sets
of acceptance rejection numbers.
• The two sample sizes may or may not be equal.
• It can be described in terms of c1,c2,n1,n2

Multiple sampling plan:
• In this 3 or more samples might be taken before a decision is
reached regarding the acceptability of a lot.
• It results in smaller average sample size.

Continuous sampling plan:
• An extreme case of multiple sampling in which sampling might
continues until the lot is exhausted.
• It calls for inspection on an item by item basis.
• Decision is made after each item is inspected concerning
whether lot should be accepted or rejected or sampling
continued.
• Sampling & decision making continues until a clear cut
decision is obtained either to accept or reject.

• Step 5 – Determine the Correct Sampling
Quantity (n).
• Step 6 – Determine Your Accept & Reject
Numbers

Operating characteristic curve
• There is always a risk that your acceptance sampling will result
in an incorrect decision to accept or reject.
• To understand the acceptance probability associated with your
acceptance plan, you can create an OC Curve to plot the
acceptance probability versus the fraction non-conforming.

Operating characteristic curve
The Operating Characteristic Curve is a plot of the probability of accepting a lot
against the a theoretical incoming quality level, p(% nonconforming). The
Probability of Acceptance Pa is plotted on the Y Axis, with the Theoretical
Incoming Lot Defect Rate on the X Axis

Advantages:
 Acceptance sampling eliminates or rectifies poor lots & improve
overall quality of product.
 Reduces inspection costs & risk.
 In inspection of sample greater care will be taken so that results
may be more accurate.
 A rejected lot is frequently a signal to the manufacturer that the
process should be improved.
 It provides a no of alternative plans in which a single sample is
taken, two or indefinite no of samples may be taken from a

Disadvantages:
• Risk included in chance of bad lot “acceptance” and good lot
“rejection”
• Sample taken provides less information than 100% inspection

Acceptance sampling

Recommended

More Related Content

What's hot (20)

Similar to Acceptance sampling (20)

More from SIBENDU SURAJEET JENA (11)

Recently uploaded (20)

Acceptance sampling

Editor's Notes