10_LectureSlides.pptx
- 1. Chapter 10 Lecture Presentation Energy and Work © 2015 Pearson Education, Inc.
- 2. Slide 10-2 Suggested Videos for Chapter 10 • Prelecture Videos • Forms of Energy • Conservation of Energy • Work and Power • Class Videos • The Basic Energy Model • Breaking Boards • Video Tutor Solutions • Energy and Work • Video Tutor Demos • Canned Food Race • Chin Basher? © 2015 Pearson Education, Inc.
- 3. Slide 10-3 Suggested Simulations for Chapter 10 • ActivPhysics • 5.1–5.7 • 6.1, 6.2, 6.5, 6.8, 6.9 • 7.11–7.13 • PhETs • Energy Skate Park • The Ramp © 2015 Pearson Education, Inc.
- 4. Slide 10-4 Chapter 10 Energy and Work Chapter Goal: To introduce the concept of energy and to learn a new problem-solving strategy based on conservation of energy. © 2015 Pearson Education, Inc.
- 5. Slide 10-5 Chapter 10 Preview Looking Ahead: Forms of Energy • This dolphin has lots of kinetic energy as it leaves the water. At its highest point its energy is mostly potential energy. • You’ll learn about several of the most important forms of energy—kinetic, potential, and thermal. © 2015 Pearson Education, Inc.
- 6. Slide 10-6 Chapter 10 Preview Looking Ahead: Work and Energy • As the band is stretched, energy is transferred to it as work. This energy is then transformed into kinetic energy of the rock. • You’ll learn how to calculate the work done by a force, and how this work is related to the change in a system’s energy. © 2015 Pearson Education, Inc.
- 7. Slide 10-7 Chapter 10 Preview Looking Ahead: Conservation of Energy • As they slide, their potential energy decreases and their kinetic energy increases, but their total energy is unchanged: It is conserved. • How fast will they be moving when they reach the bottom? You’ll use a new before-and-after analysis to find out. © 2015 Pearson Education, Inc.
- 8. Slide 10-8 Chapter 10 Preview Looking Ahead © 2015 Pearson Education, Inc. Text: p. 283
- 9. Slide 10-9 Chapter 10 Preview Looking Back: Motion with Constant Acceleration In Chapter 2 you learned how to describe the motion of a particle that has a constant acceleration. In this chapter, you’ll use the constant-acceleration equations to connect work and energy. A particle’s final velocity is related to its initial velocity, its acceleration, and its displacement by © 2015 Pearson Education, Inc. 2 2 f i 2 x x x v v a x
- 10. Section 10.1 The Basic Energy Model © 2015 Pearson Education, Inc.
- 11. Slide 10-11 The Basic Energy Model Every system in nature has a quantity we call its total energy E.
- 12. Slide 10-12 Forms of Energy Some important forms of energy are • Kinetic energy K: energy of motion. • Gravitational potential energy Ug: stored energy associated with an object’s height above the ground. • Elastic or spring potential energy Us: energy stored when a spring or other elastic object is stretched. • Thermal energy Eth: the sum of the kinetic and potential energies of all the molecules in an object. • Chemical energy Echem: energy stored in the bonds between molecules. • Nuclear energy Enuclear: energy stored in the mass of the nucleus of an atom.
- 13. Slide 10-13 Energy Transformations Energy of one kind can be transformed into energy of another kind within a system. © 2015 Pearson Education, Inc.
- 14. Slide 10-14 Energy Transformations The weightlifter converts chemical energy in her body into gravitational potential energy of the barbell. Elastic potential energy of the springboard is converted into kinetic energy. As the diver rises into the air, this kinetic energy is transformed into gravitational potential energy. © 2015 Pearson Education, Inc.
- 15. Slide 10-15 QuickCheck 10.1 A child is on a playground swing, motionless at the highest point of his arc. What energy transformation takes place as he swings back down to the lowest point of his motion? A. K Ug B. Ug K C. Eth K D. Ug Eth E. K Eth
- 16. Slide 10-16 QuickCheck 10.1 A child is on a playground swing, motionless at the highest point of his arc. What energy transformation takes place as he swings back down to the lowest point of his motion? A. K Ug B. Ug K C. Eth K D. Ug Eth E. K Eth © 2015 Pearson Education, Inc.
- 17. Slide 10-17 QuickCheck 10.2 A skier is gliding down a gentle slope at a constant speed. What energy transformation is taking place? A. K Ug B. Ug K C. Eth K D. Ug Eth E. K Eth
- 18. Slide 10-18 QuickCheck 10.2 A skier is gliding down a gentle slope at a constant speed. What energy transformation is taking place? A. K Ug B. Ug K C. Eth K D. Ug Eth E. K Eth © 2015 Pearson Education, Inc.
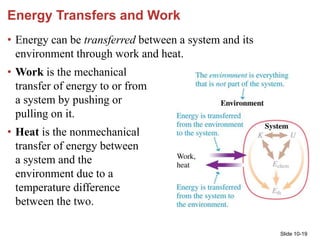
- 19. Slide 10-19 Energy Transfers and Work • Energy can be transferred between a system and its environment through work and heat. • Work is the mechanical transfer of energy to or from a system by pushing or pulling on it. • Heat is the nonmechanical transfer of energy between a system and the environment due to a temperature difference between the two.
- 20. Slide 10-20 Energy Transfers and Work The athlete does work on the shot, giving it kinetic energy, K. © 2015 Pearson Education, Inc. The hand does work on the match, giving it thermal energy, Eth. The boy does work on the slingshot, giving it elastic potential energy, Us.
- 21. Slide 10-21 QuickCheck 10.3 A tow rope pulls a skier up the slope at constant speed. What energy transfer (or transfers) is taking place? A. W Ug B. W K C. W Eth D. Both A and B. E. Both A and C.
- 22. Slide 10-22 QuickCheck 10.3 A tow rope pulls a skier up the slope at constant speed. What energy transfer (or transfers) is taking place? A. W Ug B. W K C. W Eth D. Both A and B. E. Both A and C. © 2015 Pearson Education, Inc.
- 23. Slide 10-23 The Work-Energy Equation • Work represents energy that is transferred into or out of a system. • The total energy of a system changes by the amount of work done on it. • Work can increase or decrease the energy of a system. • If no energy is transferred into or out of a system, that is an isolated system. © 2015 Pearson Education, Inc.
- 24. Slide 10-24 QuickCheck 10.4 A crane lowers a girder into place at constant speed. Consider the work Wg done by gravity and the work WT done by the tension in the cable. Which is true? A. Wg > 0 and WT > 0 B. Wg > 0 and WT < 0 C. Wg < 0 and WT > 0 D. Wg < 0 and WT < 0 E. Wg = 0 and WT = 0
- 25. Slide 10-25 QuickCheck 10.4 A crane lowers a girder into place at constant speed. Consider the work Wg done by gravity and the work WT done by the tension in the cable. Which is true? A. Wg > 0 and WT > 0 B. Wg > 0 and WT < 0 C. Wg < 0 and WT > 0 D. Wg < 0 and WT < 0 E. Wg = 0 and WT = 0 The downward force of gravity is in the direction of motion positive work. The upward tension is in the direction opposite the motion negative work. © 2015 Pearson Education, Inc.
- 26. Slide 10-26 QuickCheck 10.5 Robert pushes the box to the left at constant speed. In doing so, Robert does ______ work on the box. A. positive B. negative C. zero
- 27. Slide 10-27 QuickCheck 10.5 Robert pushes the box to the left at constant speed. In doing so, Robert does ______ work on the box. A. positive B. negative C. zero Force is in the direction of displacement positive work © 2015 Pearson Education, Inc.
- 28. Slide 10-28 The Law of Conservation of Energy The total energy of an isolated system remains constant.
- 29. Section 10.2 Work © 2015 Pearson Education, Inc.
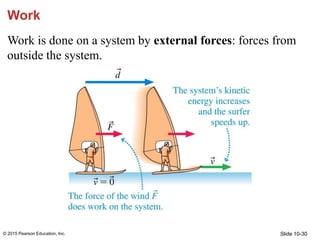
- 30. Slide 10-30 Work Work is done on a system by external forces: forces from outside the system. © 2015 Pearson Education, Inc.
- 31. Slide 10-31 Calculating Work • Although both the force and the displacement are vectors, work is a scalar. • The unit of work (and energy) is: © 2015 Pearson Education, Inc. 1 joule 1 J 1 N m
- 32. Slide 10-32 Example 10.1 Work done in pushing a crate Sarah pushes a heavy crate 3.0 m along the floor at a constant speed. She pushes with a constant horizontal force of magnitude 70 N. How much work does Sarah do on the crate?
- 33. Slide 10-33 Example 10.1 Work done in pushing a crate (cont.) PREPARE We begin with the before-and-after visual overview in FIGURE 10.6. Sarah pushes with a constant force in the direction of the crate’s motion, so we can use Equation 10.5 to find the work done. SOLVE The work done by Sarah is W = Fd = (70 N)(3.0 m) = 210 J By pushing on the crate Sarah increases its kinetic energy, so it makes sense that the work done is positive. © 2015 Pearson Education, Inc.
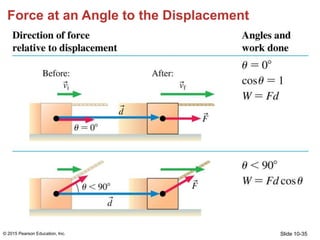
- 34. Slide 10-34 Force at an Angle to the Displacement • Only the component of a force in the direction of displacement does work. • If the force is at an angle θ to the displacement, the component of the force, F, that does work is Fcosθ. © 2015 Pearson Education, Inc.
- 35. Slide 10-35 Force at an Angle to the Displacement © 2015 Pearson Education, Inc.
- 36. Slide 10-36 Force at an Angle to the Displacement © 2015 Pearson Education, Inc.
- 37. Slide 10-37 Force at an Angle to the Displacement The sign of W is determined by the angle θ between the force and the displacement. © 2015 Pearson Education, Inc.
- 38. Slide 10-38 A constant force pushes a particle through a displacement . In which of these three cases does the force do negative work? D. Both A and B. E. Both A and C. QuickCheck 10.6
- 39. Slide 10-39 QuickCheck 10.6 A constant force pushes a particle through a displacement . In which of these three cases does the force do negative work? D. Both A and B. E. Both A and C. © 2015 Pearson Education, Inc.
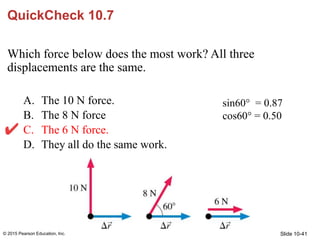
- 40. Slide 10-40 sin60 = 0.87 cos60 = 0.50 QuickCheck 10.7 Which force below does the most work? All three displacements are the same. A. The 10 N force. B. The 8 N force C. The 6 N force. D. They all do the same work.
- 41. Slide 10-41 sin60 = 0.87 cos60 = 0.50 QuickCheck 10.7 Which force below does the most work? All three displacements are the same. A. The 10 N force. B. The 8 N force C. The 6 N force. D. They all do the same work. © 2015 Pearson Education, Inc.
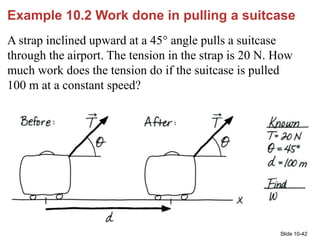
- 42. Slide 10-42 Example 10.2 Work done in pulling a suitcase A strap inclined upward at a 45° angle pulls a suitcase through the airport. The tension in the strap is 20 N. How much work does the tension do if the suitcase is pulled 100 m at a constant speed?
- 43. Slide 10-43 Example 10.2 Work done in pulling a suitcase (cont.) PREPARE FIGURE 10.8 shows a visual overview. Since the suitcase moves at a constant speed, there must be a rolling friction force (not shown) acting to the left. SOLVE We can use Equation 10.6 , with force F T, to find that the tension does work: W = Td cos = (20 N)(100 m)cos 45° = 1400 J The tension is needed to do work on the suitcase even though the suitcase is traveling at a constant speed to overcome friction. So it makes sense that the work is positive. The work done goes entirely into increasing the thermal energy of the suitcase and the floor. © 2015 Pearson Education, Inc.
- 44. Slide 10-44 Forces That Do No Work A force does no work on an object if • The object undergoes no displacement. • The force is perpendicular to the displacement. • The part of the object on which the force acts undergoes no displacement (even if other parts of the object do move). Text: p. 291
- 45. Section 10.3 Kinetic Energy © 2015 Pearson Education, Inc.
- 46. Slide 10-46 Kinetic Energy • Kinetic energy is energy of motion. • Kinetic energy can be in two forms: translational, for motion of an object along a path; and rotational, for the motion of an object around an axis. © 2015 Pearson Education, Inc.
- 47. Slide 10-47 Rotational Kinetic Energy • Rotational kinetic energy is a way of expressing the sum of the kinetic energy of all the parts of a rotating object. • In rotational kinetic energy, the moment of inertia takes the place of mass and the angular velocity takes the place of linear velocity. © 2015 Pearson Education, Inc.
- 48. Slide 10-48 Example 10.5 Speed of a bobsled after pushing A two-man bobsled has a mass of 390 kg. Starting from rest, the two racers push the sled for the first 50 m with a net force of 270 N. Neglecting friction, what is the sled’s speed at the end of the 50 m?
- 49. Slide 10-49 Example 10.5 Speed of a bobsled after pushing (cont.) PREPARE Because friction is negligible, there is no change in the sled’s thermal energy. And, because the sled’s height is constant, its gravitational potential energy is unchanged as well. Thus the work-energy equation is simply ΔK = W. We can therefore find the sled’s final kinetic energy, and hence its speed, by finding the work done by the racers as they push on the sled. The figure lists the known quantities and the quantity vf that we want to find. The work done by the pushers increases the sled’s kinetic energy. © 2015 Pearson Education, Inc.
- 50. Slide 10-50 Example 10.5 Speed of a bobsled after pushing (cont.) SOLVE From the work-energy equation, Equation 10.3, the change in the sled’s kinetic energy is ΔK = Kf Ki = W. The sled’s final kinetic energy is thus Kf = Ki + W Using our expressions for kinetic energy and work, we get Because vi = 0, the work-energy equation reduces to . We can solve for the final speed to get © 2015 Pearson Education, Inc.
- 51. Slide 10-51 QuickCheck 10.10 A light plastic cart and a heavy steel cart are both pushed with the same force for a distance of 1.0 m, starting from rest. After the force is removed, the kinetic energy of the light plastic cart is ________ that of the heavy steel cart. A. greater than B. equal to C. less than D. Can’t say. It depends on how big the force is.
- 52. Slide 10-52 QuickCheck 10.10 A light plastic cart and a heavy steel cart are both pushed with the same force for a distance of 1.0 m, starting from rest. After the force is removed, the kinetic energy of the light plastic cart is ________ that of the heavy steel cart. A. greater than B. equal to C. less than D. Can’t say. It depends on how big the force is. © 2015 Pearson Education, Inc. Same force, same distance same work done Same work change of kinetic energy
- 53. Slide 10-53 QuickCheck 10.11 Each of the boxes shown is pulled for 10 m across a level, frictionless floor by the force given. Which box experiences the greatest change in its kinetic energy?
- 54. Slide 10-54 D QuickCheck 10.11 Each of the boxes shown is pulled for 10 m across a level, frictionless floor by the force given. Which box experiences the greatest change in its kinetic energy? © 2015 Pearson Education, Inc. Work-energy equation: ∆K = W = Fd. All have same d, so largest work (and hence largest ∆K) corresponds to largest force.
- 55. Slide 10-55 QuickCheck 10.12 Each of the 1.0 kg boxes starts at rest and is then is pulled for 2.0 m across a level, frictionless floor by a rope with the noted force at the noted angle. Which box has the highest final speed?
- 56. Slide 10-56 QuickCheck 10.12 Each of the 1.0 kg boxes starts at rest and is then is pulled for 2.0 m across a level, frictionless floor by a rope with the noted force at the noted angle. Which box has the highest final speed? © 2015 Pearson Education, Inc. B
- 57. Section 10.4 Potential Energy © 2015 Pearson Education, Inc.
- 58. Slide 10-58 Potential Energy • Potential energy is stored energy that can be readily converted to other forms of energy, such as kinetic or thermal energy. • Forces that can store useful energy are conservative forces: • Gravity • Elastic forces • Forces such as friction that cannot store useful energy are nonconservative forces. © 2015 Pearson Education, Inc.
- 59. Slide 10-59 Gravitational Potential Energy The change in gravitational potential energy is proportional to the change in its height. © 2015 Pearson Education, Inc.
- 60. Slide 10-60 Gravitational Potential Energy • We can choose the reference level where gravitational potential energy Ug = 0 since only changes in Ug matter. • Because gravity is a conservative force, gravitational potential energy depends only on the height of an object and not on the path the object took to get to that height. © 2015 Pearson Education, Inc.
- 61. Slide 10-61 QuickCheck 10.13 Rank in order, from largest to smallest, the gravitational potential energies of the balls. A. 1 > 2 = 4 > 3 B. 1 > 2 > 3 > 4 C. 3 > 2 > 4 > 1 D. 3 > 2 = 4 > 1
- 62. Slide 10-62 QuickCheck 10.13 Rank in order, from largest to smallest, the gravitational potential energies of the balls. A. 1 > 2 = 4 > 3 B. 1 > 2 > 3 > 4 C. 3 > 2 > 4 > 1 D. 3 > 2 = 4 > 1 © 2015 Pearson Education, Inc.
- 63. Slide 10-63 QuickCheck 10.14 Starting from rest, a marble first rolls down a steeper hill, then down a less steep hill of the same height. For which is it going faster at the bottom? A. Faster at the bottom of the steeper hill. B. Faster at the bottom of the less steep hill. C. Same speed at the bottom of both hills. D. Can’t say without knowing the mass of the marble.
- 64. Slide 10-64 QuickCheck 10.14 Starting from rest, a marble first rolls down a steeper hill, then down a less steep hill of the same height. For which is it going faster at the bottom? A. Faster at the bottom of the steeper hill. B. Faster at the bottom of the less steep hill. C. Same speed at the bottom of both hills. D. Can’t say without knowing the mass of the marble. © 2015 Pearson Education, Inc.
- 65. Slide 10-65 QuickCheck 10.15 A small child slides down the four frictionless slides A–D. Rank in order, from largest to smallest, her speeds at the bottom. A. vD > vA > vB > vC B. vD > vA = vB > vC C. vC > vA > vB > vD D. vA = vB = vC = vD
- 66. Slide 10-66 QuickCheck 10.15 A small child slides down the four frictionless slides A–D. Rank in order, from largest to smallest, her speeds at the bottom. A. vD > vA > vB > vC B. vD > vA = vB > vC C. vC > vA > vB > vD D. vA = vB = vC = vD © 2015 Pearson Education, Inc.
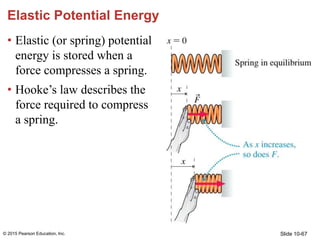
- 67. Slide 10-67 Elastic Potential Energy • Elastic (or spring) potential energy is stored when a force compresses a spring. • Hooke’s law describes the force required to compress a spring. © 2015 Pearson Education, Inc.
- 68. Slide 10-68 Elastic Potential Energy The elastic potential energy stored in a spring is determined by the average force required to compress the spring from its equilibrium length. © 2015 Pearson Education, Inc.
- 69. Slide 10-69 QuickCheck 10.16 Three balls are thrown from a cliff with the same speed but at different angles. Which ball has the greatest speed just before it hits the ground? A. Ball A. B. Ball B. C. Ball C. D. All balls have the same speed. © 2015 Pearson Education, Inc.
- 70. Slide 10-70 QuickCheck 10.16 Three balls are thrown from a cliff with the same speed but at different angles. Which ball has the greatest speed just before it hits the ground? A. Ball A. B. Ball B. C. Ball C. D. All balls have the same speed.
- 71. Slide 10-71 QuickCheck 10.17 A hockey puck sliding on smooth ice at 4 m/s comes to a 1-m-high hill. Will it make it to the top of the hill? A. Yes. B. No. C. Can’t answer without knowing the mass of the puck. D. Can’t say without knowing the angle of the hill.
- 72. Slide 10-72 QuickCheck 10.17 A hockey puck sliding on smooth ice at 4 m/s comes to a 1-m-high hill. Will it make it to the top of the hill? A. Yes. B. No. C. Can’t answer without knowing the mass of the puck. D. Can’t say without knowing the angle of the hill. © 2015 Pearson Education, Inc.
- 73. Slide 10-73 Example 10.8 Pulling back on a bow An archer pulls back the string on her bow to a distance of 70 cm from its equilibrium position. To hold the string at this position takes a force of 140 N. How much elastic potential energy is stored in the bow?
- 74. Slide 10-74 Example 10.8 Pulling back on a bow An archer pulls back the string on her bow to a distance of 70 cm from its equilibrium position. To hold the string at this position takes a force of 140 N. How much elastic potential energy is stored in the bow? PREPARE A bow is an elastic material, so we will model it as obeying Hooke’s law, Fs = kx, where x is the distance the string is pulled back. We can use the force required to hold the string, and the distance it is pulled back, to find the bow’s spring constant k. Then we can use Equation 10.15 to find the elastic potential energy. © 2015 Pearson Education, Inc.
- 75. Slide 10-75 Example 10.8 Pulling back on a bow (cont.) SOLVE From Hooke’s law, the spring constant is Then the elastic potential energy of the flexed bow is ASSESS When the arrow is released, this elastic potential energy will be transformed into the kinetic energy of the arrow. According to Table 10.1, the kinetic energy of a 100 mph fastball is about 150 J, so 49 J of kinetic energy for a fast-moving arrow seems reasonable. © 2015 Pearson Education, Inc.
- 76. Section 10.5 Thermal Energy © 2015 Pearson Education, Inc.
- 77. Slide 10-77 Thermal Energy Thermal energy is the sum of the kinetic energy of atoms and molecules in a substance and the elastic potential energy stored in the molecular bonds between atoms. © 2015 Pearson Education, Inc.
- 78. Slide 10-78 Creating Thermal Energy Friction on a moving object does work. That work creates thermal energy. © 2015 Pearson Education, Inc.
- 79. Slide 10-79 Example 10.9 Creating thermal energy by rubbing A 0.30 kg block of wood is rubbed back and forth against a wood table 30 times in each direction. The block is moved 8.0 cm during each stroke and pressed against the table with a force of 22 N. How much thermal energy is created in this process?
- 80. Slide 10-80 Example 10.9 Creating thermal energy by rubbing A 0.30 kg block of wood is rubbed back and forth against a wood table 30 times in each direction. The block is moved 8.0 cm during each stroke and pressed against the table with a force of 22 N. How much thermal energy is created in this process? PREPARE The hand holding the block does work to push the block back and forth. Work transfers energy into the block table system, where it appears as thermal energy according to Equation 10.16. The force of friction can be found from the model of kinetic friction introduced in Chapter 5, fk = kn; from Table 5.2 the coefficient of kinetic friction for wood sliding on wood is k = 0.20. © 2015 Pearson Education, Inc.
- 81. Slide 10-81 Example 10.9 Creating thermal energy by rubbing (cont.) To find the normal force n acting on the block, we draw the free-body diagram of the figure, which shows only the vertical forces acting on the block. © 2015 Pearson Education, Inc.
- 82. Slide 10-82 Example 10.9 Creating thermal energy by rubbing (cont.) SOLVE From Equation 10.16 we have ΔEth = fk Δx, where fk = kn. The block is not accelerating in the y-direction, so from the free-body diagram Newton’s second law gives Fy = n w F = may = 0 or n = w + F = mg + F = (0.30 kg)(9.8 m/s2) + 22 N = 24.9 N The friction force is then fk = kn = (0.20)(24.9 N) = 4.98 N. The total displacement of the block is 2 30 8.0 cm = 4.8 m. Thus the thermal energy created is ΔEth = fk Δx = (4.98 N)(4.8 m) = 24 J ASSESS This modest amount of thermal energy seems reasonable for a person to create by rubbing. © 2015 Pearson Education, Inc.
- 83. Slide 10-83 Try It Yourself: Agitating Atoms Vigorously rub a somewhat soft object such as a blackboard eraser on your desktop for about 10 seconds. If you then pass your fingers over the spot where you rubbed, you’ll feel a distinct warm area. Congratulations: You’ve just set some 100,000,000,000,000,000,000,000 atoms into motion! © 2015 Pearson Education, Inc.
- 84. Section 10.6 Using the Law of Conservation of Energy © 2015 Pearson Education, Inc.
- 85. Slide 10-85 Using the Law of Conservation of Energy • We can use the law of conservation of energy to develop a before-and-after perspective for energy conservation: ∆K + ∆Ug + ∆Us + ∆Eth = W Kf + (Ug)f + (Us)f + ∆Eth = Ki + (Ug)i + (Us)i + W • This is analogous to the before-and-after approach used with the law of conservation of momentum. • In an isolated system, W = 0: Kf + (Ug)f + (Us)f + ∆Eth = Ki + (Ug)i + (Us)i © 2015 Pearson Education, Inc.
- 86. Slide 10-86 Choosing an Isolated System © 2015 Pearson Education, Inc. Text: p. 300
- 87. Slide 10-87 QuickCheck 10.18 A spring-loaded gun shoots a plastic ball with a launch speed of 2.0 m/s. If the spring is compressed twice as far, the ball’s launch speed will be A. 1.0 m/s B. 2.0 m/s C. 2.8 m/s D. 4.0 m/s E. 16.0 m/s
- 88. Slide 10-88 QuickCheck 10.18 A spring-loaded gun shoots a plastic ball with a launch speed of 2.0 m/s. If the spring is compressed twice as far, the ball’s launch speed will be A. 1.0 m/s B. 2.0 m/s C. 2.8 m/s D. 4.0 m/s E. 16.0 m/s Conservation of energy: Double x double v
- 89. Slide 10-89 QuickCheck 10.19 A spring-loaded gun shoots a plastic ball with a launch speed of 2.0 m/s. If the spring is replaced with a new spring having twice the spring constant (but still compressed the same distance), the ball’s launch speed will be A. 1.0 m/s B. 2.0 m/s C. 2.8 m/s D. 4.0 m/s E. 16.0 m/s
- 90. Slide 10-90 QuickCheck 10.19 A spring-loaded gun shoots a plastic ball with a launch speed of 2.0 m/s. If the spring is replaced with a new spring having twice the spring constant (but still compressed the same distance), the ball’s launch speed will be A. 1.0 m/s B. 2.0 m/s C. 2.8 m/s D. 4.0 m/s E. 16.0 m/s Conservation of energy: Double k increase v by square root of 2
- 91. Slide 10-91 Example Problem A car sits at rest at the top of a hill. A small push sends it rolling down the hill. After its height has dropped by 5.0 m, it is moving at a good clip. Write down the equation for conservation of energy, noting the choice of system, the initial and final states, and what energy transformation has taken place.
- 92. Slide 10-92 Example Problem A child slides down a slide at a constant speed of 1.5 m/s. The height of the slide is 3.0 m. Write down the equation for conservation of energy, noting the choice of system, the initial and final states, and what energy transformation has taken place.
- 93. Slide 10-93 Example 10.11 Speed at the bottom of a water slide While at the county fair, Katie tries the water slide, whose shape is shown in the figure. The starting point is 9.0 m above the ground. She pushes off with an initial speed of 2.0 m/s. If the slide is frictionless, how fast will Katie be traveling at the bottom?
- 94. Slide 10-94
- 95. Slide 10-95 Example 10.11 Speed at the bottom of a water slide (cont.) PREPARE Table 10.2 showed that the system consisting of Katie and the earth is isolated because the normal force of the slide is perpendicular to Katie’s motion and does no work. If we assume the slide is frictionless, we can use the conservation of mechanical energy equation. SOLVE Conservation of mechanical energy gives Kf + (Ug)f = Ki + (Ug)i or © 2015 Pearson Education, Inc.
- 96. Slide 10-96 Example 10.11 Speed at the bottom of a water slide (cont.) Taking yf = 0 m, we have which we can solve to get Notice that the shape of the slide does not matter because gravitational potential energy depends only on the height above a reference level. © 2015 Pearson Education, Inc.
- 97. Slide 10-97 Example 10.13 Pulling a bike trailer Monica pulls her daughter Jessie in a bike trailer. The trailer and Jessie together have a mass of 25 kg. Monica starts up a 100-m-long slope that’s 4.0 m high. On the slope, Monica’s bike pulls on the trailer with a constant force of 8.0 N. They start out at the bottom of the slope with a speed of 5.3 m/s. What is their speed at the top of the slope?
- 98. Slide 10-98 Example 10.13 Pulling a bike trailer (cont.) PREPARE Taking Jessie and the trailer as the system, we see that Monica’s bike is applying a force to the system as it moves through a displacement; that is, Monica’s bike is doing work on the system. Thus we’ll need to use the full version of Equation 10.18, including the work term W. © 2015 Pearson Education, Inc.
- 99. Slide 10-99 Example 10.13 Pulling a bike trailer (cont.) SOLVE If we assume there’s no friction, so that ΔEth = 0, then Equation 10.18 is Kf + (Ug)f = Ki + (Ug)i + W or © 2015 Pearson Education, Inc.
- 100. Slide 10-100 Example 10.13 Pulling a bike trailer (cont.) Taking yi = 0 m and writing W = Fd, we can solve for the final speed: from which we find that vf = 3.7 m/s. Note that we took the work to be a positive quantity because the force is in the same direction as the displacement. ASSESS A speed of 3.7 m/s—about 8 mph—seems reasonable for a bicycle’s speed. Jessie’s final speed is less than her initial speed, indicating that the uphill force of Monica’s bike on the trailer is less than the downhill component of gravity. © 2015 Pearson Education, Inc.
- 101. Slide 10-101 Energy and Its Conservation © 2015 Pearson Education, Inc. Text: p. 304
- 102. Slide 10-102 Energy and Its Conservation © 2015 Pearson Education, Inc. Text: p. 304
- 103. Section 10.7 Energy in Collisions © 2015 Pearson Education, Inc.
- 104. Slide 10-104 Energy in Collisions • A collision in which the colliding objects stick together and then move with a common final velocity is a perfectly inelastic collision. • A collision in which mechanical energy is conserved is called a perfectly elastic collision. • While momentum is conserved in all collisions, mechanical energy is only conserved in a perfectly elastic collision. • In an inelastic collision, some mechanical energy is converted to thermal energy. © 2015 Pearson Education, Inc.
- 105. Slide 10-105 Example 10.15 Energy transformations in a perfectly inelastic collision The figure shows two train cars that move toward each other, collide, and couple together. In Example 9.8, we used conservation of momentum to find the final velocity shown in the figure from the given initial velocities. How much thermal energy is created in this collision?
- 106. Slide 10-106 Example 10.15 Energy transformations in a perfectly inelastic collision (cont.) PREPARE We’ll choose our system to be the two cars. Because the track is horizontal, there is no change in potential energy. Thus the law of conservation of energy, Equation 10.18a, is Kf + ΔEth = Ki. The total energy before the collision must equal the total energy afterward, but the mechanical energies need not be equal. © 2015 Pearson Education, Inc.
- 107. Slide 10-107 Example 10.15 Energy transformations in a perfectly inelastic collision (cont.) SOLVE The initial kinetic energy is Because the cars stick together and move as a single object with mass m1 + m2, the final kinetic energy is © 2015 Pearson Education, Inc.
- 108. Slide 10-108 Example 10.15 Energy transformations in a perfectly inelastic collision (cont.) From the conservation of energy equation on the previous slide, we find that the thermal energy increases by ΔEth = Ki Kf = 4.7 104 J 1900 J = 4.5 104 J This amount of the initial kinetic energy is transformed into thermal energy during the impact of the collision. ASSESS About 96% of the initial kinetic energy is transformed into thermal energy. This is typical of many real-world collisions. © 2015 Pearson Education, Inc.
- 109. Slide 10-109 Elastic Collisions Elastic collisions obey conservation of momentum and conservation of mechanical energy. © 2015 Pearson Education, Inc. 1 1 i 1 1 f 2 2 f ( ) ( ) ( ) x x x m v m v m v 2 2 2 1 1 i 1 1 f 2 2 f 1 1 1 ( ) ( ) ( ) 2 2 2 x x x m v m v m v Momentum: Energy:
- 110. Slide 10-110 Example 10.16 Velocities in an air hockey collision On an air hockey table, a moving puck, traveling to the right at 2.3 m/s, makes a head-on collision with an identical puck at rest. What is the final velocity of each puck?
- 111. Slide 10-111
- 112. Slide 10-112 Example 10.16 Velocities in an air hockey collision (cont.) PREPARE The before-and-after visual overview is shown in the figure. We’ve shown the final velocities in the picture, but we don’t really know yet which way the pucks will move. Because one puck was initially at rest, we can use Equations 10.20 to find the final velocities of the pucks. The pucks are identical, so we have m1 = m2 = m. © 2015 Pearson Education, Inc.
- 113. Slide 10-113 Example 10.16 Velocities in an air hockey collision (cont.) SOLVE We use Equations 10.20 with m1 = m2 = m to get The incoming puck stops dead, and the initially stationary puck goes off with the same velocity that the incoming one had. © 2015 Pearson Education, Inc.
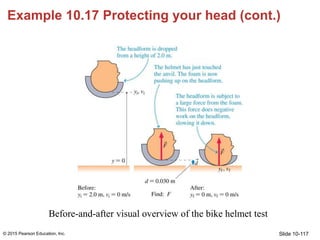
- 114. Slide 10-114 A bike helmet—basically a shell of hard, crushable foam—is tested by being strapped onto a 5.0 kg headform and dropped from a height of 2.0 m onto a hard anvil. What force is encountered by the headform if the impact crushes the foam by 3.0 cm? Example 10.17 Protecting your head
- 115. Slide 10-115
- 116. Slide 10-116 A bike helmet—basically a shell of hard, crushable foam—is tested by being strapped onto a 5.0 kg headform and dropped from a height of 2.0 m onto a hard anvil. What force is encountered by the headform if the impact crushes the foam by 3.0 cm? PREPARE We can use the work-energy equation, Equation 10.18, to calculate the force on the headform. We’ll choose the headform and the earth to be the system; the foam in the helmet is part of the environment. We make this choice so that the force on the headform due to the foam is an external force that does work W on the headform. Example 10.17 Protecting your head © 2015 Pearson Education, Inc.
- 117. Slide 10-117 Example 10.17 Protecting your head (cont.) Before-and-after visual overview of the bike helmet test © 2015 Pearson Education, Inc.
- 118. Slide 10-118 Example 10.17 Protecting your head (cont.) SOLVE The headform starts at rest, speeds up as it falls, then returns to rest during the impact. Overall, then, Kf = Ki. Furthermore, ΔEth = 0 because there’s no friction to increase the thermal energy. Only the gravitational potential energy changes, so the work-energy equation is (Ug)f (Ug)i = W The upward force of the foam on the headform is opposite the downward displacement of the headform. Referring to Tactics Box 10.1, we see that the work done is negative: W = Fd, where we’ve assumed that the force is constant. Using this result in the work-energy equation and solving for F, we find © 2015 Pearson Education, Inc.
- 119. Slide 10-119 Example 10.17 Protecting your head (cont.) Taking our reference height to be y = 0 m at the anvil, we have (Ug)f = 0. We’re left with (Ug)i = mgyi, so This is the force that acts on the head to bring it to a halt in 3.0 cm. More important from the perspective of possible brain injury is the head’s acceleration: ASSESS The accepted threshold for serious brain injury is around 300g, so this helmet would protect the rider in all but the most serious accidents. Without the helmet, the rider’s head would come to a stop in a much shorter distance and thus be subjected to a much larger acceleration. © 2015 Pearson Education, Inc.
- 120. Section 10.8 Power © 2015 Pearson Education, Inc.
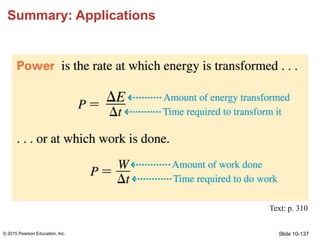
- 121. Slide 10-121 Power • Power is the rate at which energy is transformed or transferred. • The unit of power is the watt: 1 watt = 1 W = 1 J/s © 2015 Pearson Education, Inc.
- 122. Slide 10-122 Output Power of a Force • A force doing work transfers energy. • The rate that this force transfers energy is the output power of that force: © 2015 Pearson Education, Inc.
- 123. Slide 10-123 QuickCheck 10.20 Four students run up the stairs in the time shown. Which student has the largest power output?
- 124. Slide 10-124 QuickCheck 10.20 Four students run up the stairs in the time shown. Which student has the largest power output? © 2015 Pearson Education, Inc. B.
- 125. Slide 10-125 QuickCheck 10.21 Four toy cars accelerate from rest to their top speed in a certain amount of time. The masses of the cars, the final speeds, and the time to reach this speed are noted in the table. Which car has the greatest power?
- 126. Slide 10-126 QuickCheck 10.21 Four toy cars accelerate from rest to their top speed in a certain amount of time. The masses of the cars, the final speeds, and the time to reach this speed are noted in the table. Which car has the greatest power? © 2015 Pearson Education, Inc.
- 127. Slide 10-127 Example 10.18 Power to pass a truck Your 1500 kg car is behind a truck traveling at 60 mph (27 m/s). To pass the truck, you speed up to 75 mph (34 m/s) in 6.0 s. What engine power is required to do this?
- 128. Slide 10-128 Example 10.18 Power to pass a truck Your 1500 kg car is behind a truck traveling at 60 mph (27 m/s). To pass the truck, you speed up to 75 mph (34 m/s) in 6.0 s. What engine power is required to do this? PREPARE Your engine is transforming the chemical energy of its fuel into the kinetic energy of the car. We can calculate the rate of transformation by finding the change ΔK in the kinetic energy and using the known time interval. © 2015 Pearson Education, Inc.
- 129. Slide 10-129 Example 10.18 Power to pass a truck (cont.) SOLVE We have so that ΔK = Kf Ki = (8.67 105 J) (5.47 105 J) = 3.20 105 J To transform this amount of energy in 6 s, the power required is This is about 71 hp. This power is in addition to the power needed to overcome drag and friction and cruise at 60 mph, so the total power required from the engine will be even greater than this. © 2015 Pearson Education, Inc.
- 130. Slide 10-130 Summary: General Principles © 2015 Pearson Education, Inc. Text: p. 310
- 131. Slide 10-131 Summary: General Principles © 2015 Pearson Education, Inc. Text: p. 310
- 132. Slide 10-132 Summary: General Principles © 2015 Pearson Education, Inc. Text: p. 310
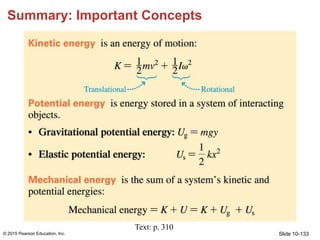
- 133. Slide 10-133 Summary: Important Concepts © 2015 Pearson Education, Inc. Text: p. 310
- 134. Slide 10-134 Summary: Important Concepts © 2015 Pearson Education, Inc. Text: p. 310
- 135. Slide 10-135 Summary: Important Concepts © 2015 Pearson Education, Inc. Text: p. 310
- 136. Slide 10-136 Summary: Applications © 2015 Pearson Education, Inc. Text: p. 310
- 137. Slide 10-137 Summary: Applications © 2015 Pearson Education, Inc. Text: p. 310
- 138. Slide 10-138 Summary © 2015 Pearson Education, Inc. Text: p. 310
- 139. Slide 10-139 Summary © 2015 Pearson Education, Inc. Text: p. 310
- 140. Slide 10-140 Summary © 2015 Pearson Education, Inc. Text: p. 310
Editor's Notes
- The Prelecture Videos are available online in the Study Area of MasteringPhysics; the Class Videos, Video Tutor Solutions, and Video Tutor Demos are available online in the Study Area of MasteringPhysics and via links within the Pearson eText.
- The ActivPhysics applets are available online in the Study Area of Mastering Physics and on the Instructor Resource DVD; the PhET simulations are available online in the Study Area of Mastering Physics.
- 15
- 16
- 17
- 18
- 21
- 22
- 24
- 25
- 26
- 27
- 38
- 39
- 40
- 41
- 51
- 52
- 53
- 54
- 55
- 56
- 61
- 62
- 63
- 64
- 65
- 66
- 69
- 70
- 71
- 72
- 87
- 88
- 89
- 90
- Answer: The system is the car. The “small push” indicates that its initial kinetic energy can be considered to be zero. We also neglect any work done by non-conservative forces. Thus, gravitational potential energy is converted into kinetic energy. For convenience we choose the bottom of the hill to be the reference point for gravitational potential energy (the bottom of the hill is at y = 0). The expression for conservation of energy for this system is thus: Kf + (Ug)f = Ki + (Ug)i. Ki = 0 (Ug)f = 0 So the final kinetic energy, Kf, is equal to the initial gravitational potential energy, (Ug)i. Since both quantities are proportional to mass, we have 𝑣= 𝑔 ℎ 𝑖 = 9.8 ×5 = 7 m/s.
- Answer: The system is the child. Because the movement is at a constant speed, work is done on the child by the slide. The expression for conservation of energy for this system is thus: Kf + (Ug)f + Eth = Ki + (Ug)i. Because the speed is constant, the kinetic energy is constant and the initial gravitational energy is converted into thermal energy.
- 123
- 124
- 125
- 126