暗号理論_エンジニア勉強会20140509
- 1. 暗号理論
- 2. おこなったこと 代数学 暗号理論 暗号の脆弱性追求 暗号解読のアルゴリズム解析 解読プログラム作成
- 3. 本日の説明 ちょっと数学 暗号紹介 暗号解析 JohannesA. Buchmann(2004) 『 INTRODUCTIONTO CRIPTOGRAPHY』 Springer(281pp) 引用元:自己撮影
- 7. 合同 定義:a,b,mに関して次の性質をもつとき、 aはmを法としてbと合同という。 性質:b-aがmを割り切る。 このとき、a≡b mod m とかく。 例:a=3,b=8,m=5 b-a=5 は m=5 を割り切る。 ※mで割ったときの余りが同じということ。
- 9. 合同”≡”は同値関係を形成する。 ①a≡a mod m OK! ②a≡b mod m なら b≡a mod m OK! ③a≡b mod m ,b≡c mod m なら a≡c mod m OK! この定義より、”=”や”∽”も同値です。 しかし≧は同値ではありません。 なぜなら②a≧bならb≧a を満たさないから。
- 10. Q,合同に関する方程式 ①X≡2 mod 4 ②X≡1mod 3 ③X≡0 mod 5 をすべて満たすxは??
- 12. 中国剰余定理 X≡a1 mod m1 X≡a2 mod m2 X≡a3 mod m3 (m1,m2,m3は互いに素)をみたす 最小のxを求める。 m=m1*m2*m3, M1=m/m1,M2=m/m2,M3=m/m3 とするとき Yi*Mi≡1mod mi (i=1,2,3)となるYiをもとめる。 すると、X=∑ai*yi*Mi mod m (1≦i≦3)となる。
- 13. ①X≡2 mod 4 ②X≡1mod 3 ③X≡0 mod 5 に適応させる。 m=4*3*5=60 M1=60/4=15,M2=60/3=20,M3=60/5=12 15Y1≡1mod 4 ⇒Y1= 3 20Y2≡1mod 3 ⇒Y2= 2 12Y3≡1mod 5 ⇒Y3= 3 ∴X=2*3*15+1*2*20+0*3*12=130≡10mod60
- 15. 証明 Yi*Mi≡1mod mi より両辺にaiをかけて aiYiMi≡ai mod mi ① miはMj(i≠j)の約数になるので Mjの倍数はmiで割り切られます。 つまり、ajYjMj ≡0 mod mi よって、∑ ajYjMj ≡0 mod mi (I≦j≠i≦n) ② ∴x=①+②= aiYiMi+ ∑ ajYjMj (I≦j≠i≦n) = ∑ aiYiMi(I≦i≦n)≡ai mod mi
- 17. 暗号系とは 次のすべての性質を満たす(P,C,K,ε、D)を 暗号系という。 ①Pは集合、Plaintext(平文) ②Cは集合、Ciphertext(暗号文) ③Kは集合、鍵空間で元kを鍵という。(k∈K) ④ε={Ek (k∈K) }は集合、暗号化関数 ⑤D= {Dk (k∈K) }は集合、復号化関数 ⑥ ∀e∈K 、 ∃d ∈K s.t. Dd(Ee(p))=p (p∈P) (⑥は暗号化したら、絶対復号できるということ。)
- 19. 対称鍵暗号系の例 ①シーザー暗号: abcdefghijklmnopqrstuvwxyz 01234・・・25 test⇒19,4,18,19 鍵k=3だとすると、 Ek( 19,4,18,19 )=(22,7,21,22)=whvw 25をオーバーしたら0に戻ります。 28 mod 26 = 2 (28≡2 mod 26)
- 21. ③アフィン暗号 長さnのブロックに対し、n*n正方行列と、 nベクトルを鍵としてHogeHogeする。 v∈P、k=(A,b) ∈K Ek:ℤm^n → ℤm^n (v↦Av+b mod m) Dk:ℤm^n → ℤm^n (v↦A^(-1)v-b mod m) ※因みに鍵k=Aのみなら、ヒル暗号 k=bのみならヴィジュネル暗号という
- 22. 例:n=2、ab(0,1)を暗号化 A= b= →A +b= =dg →A^(-1)( - )= =ab
- 26. 公開鍵暗号の例 RSA暗号:素数ベースの暗号系 ある2つの大きな素数p,qがある。 n=pqとする。 1<e<(p-1)(q-1) かつgcd(e,(p-1)(q-1))=1をみたす eを選択する。 ed≡1 mod (p-1)(q-1)) をみたすd(1<e<(p-1)(q-1))を 計算する。 (このようなdの存在は証明できる。(省略)) 公開鍵は、(n,e) 秘密鍵は、dとなる。
- 28. RSAの暗号化、復号化 ・平文mの暗号化 暗号文c=m^e mod n ・暗号文cの復号化 平文m=c^d mod n c^d=(m^e)^d=m^ed=m(ed≡1より)
- 33. 離散対数(DL) 素数pを決定する。 またpの原子根gを選ぶ。 あるA(1≦A≦p)に対して、 A≡g^a mod p となるaを離散対数という。 このaの計算は数学的に難しい。 素数についで、暗号の安全性を担うものである。 原子根:p=13の原子根は2,6,7,11 2,4,8,3,6,12,11,9,5,10,7,1,2,4,8…. と巡回するもの。
- 34. Diffie-Hellman Key Exchange 離散対数を使った、鍵の交換。 公開しているp,gを使う。 Αさんは、aを決定し A=g^a mod pの結果AをBに贈る。 Bさんは、bを決定し B=g^b mod pの結果BをAに贈る ABの共通の鍵k=g^ab mod p をえる。
- 36. 暗号化、復号化 暗号化:平文m、暗号文c 新たにbを決定する。 B=g^b mod p を計算する。 またそのbでc=A^b*m mod p と暗号化する。暗号文は(B,c) 復号化: x=p-1-aとすると m=B^x*c mod p となる。
- 37. 例:Aさんの公開鍵(p.q.A)=(23,7,4),秘密鍵a=6 (7の6乗 mod 23 =4 となる。117649÷23 =5115…4) 平文7をBさんはb=3を使い暗号化 B=g^3 mod p =21 c=A^b*m mod p =11 (21,11)をAさんに送信 AさんはB^(p-1-6)*c mod p =7 よってAさんはBさんからの平文を得た。
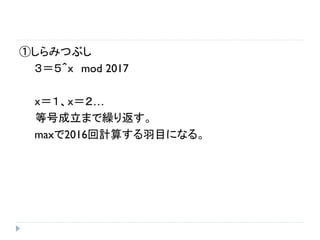
- 40. ②Shanks Baby-Step Giant-Step a = γ^x mod n 3 = 5^x mod 2017 m=floor(sqrt(2017))=45 x=qm+r とする。 Baby-Step Giant-Step は qとrを求める作業である。 B={(aγ^(-r),r)} (0≦r≦m)を計45個計算 Bの元で、(1、r)とあらわせるものがあれば、 x=rとなる。
- 43. 御清聴ありがとうございます。