3 finite

ISSN: 2319-8753
International Journal of Innovative Research in Science, Engineering and Technology
Vol. 2, Issue 5, May 2013
Finite Element Analysis of Induction Furnace
for Optimum Heat Transfer
Nihar P Bara
PG Student, Department of Mechanical Engineering, RK University, Rajkot, India
Abstract: The heat transfer characteristics of the composite wall of the induction furnace need to be evaluated for the
efficient operation. The extrusion industries are keenly involved in improving their efficiency of the induction furnace
to melt brass material by performing the modifications in the furnace and have modified the wall thickness of
composite without prior computational calculation but purely based on their experience. The objective of the present
work is to computationally validate the currently modified composite wall of induction furnace for required heat
transfer using Finite Element Method (FEM) considering transient heat conduction and to perform the structural
analysis for the determination of thermal stress in different working condition. The objectives are carefully selected to
assist the extrusion industries to efficiently use their induction furnace by performing the computation work to fully
understand its behaviour with different working condition.
Keywords:Induction Process, Thermal Analysis, Heat transfer, Wall thickness.
I. INTRODUCTION
Induction heating processes have become increasingly used in these last years in industry. The main advantages of
using these processes when compared to any other heating process (gas furnace.) are, among others, their fast heating
rate, good reproducibility and low energy consumption. The induction heating process basically consists in transmitting
by electromagnetic means, energy from a coil through which an alternative current is circulating. Induced currents in
the conductive part due to the well-known Foucault law then heat the workpiece thanks to the Joule effect. Induction
heating processes are mainly used either at low frequencies (around 50 Hz), usually in order to reach a temperature
distribution as uniform as possible within the material before any forming process, or at much higher frequencies (104–
106 Hz) in order to heat very locally near the surface, usually for heat treatments[1].
Fig.1 Furnace used in Industries
The basic induction model is shown in the Fig.1. The extrusion industries use the furnace for heating of metal for their
processes. The structure of furnace consists of inner space for metal melting, ramming mass for effective heat transfer
and induction coil for the supply of heat. The design of induction furnace involves in the proper composition of the
composite wall for the proper melting of metals. There are numerical calculations involved in the wall thickness but the
industries fit the wall thickness mostly based on experience. Most induction heating processes are set up using
engineering experience and a trial-and-error procedure in order to achieve the corresponding goal (grain size control,
uniform prescribed temperature, hardness map, etc.). Induction heating process simulation, which couples
electromagnetic and heat transfer equations, can be of great help for a more in depth understanding of occurring
physical phenomena. So far, various numerical models have been developed coupling electromagnetism and heat
transfer. Most models involve the well-known finite element approach or mixed finite element and boundary element
approaches.
Copyright to IJIRSET www.ijirset.com 1313

ISSN: 2319-8753
The recent research papers have been studied carefully and the papers related closely with the present work have been
discussed in the subsequent paragraphs. The work related with the induction furnace has been analysed by different
researchers in many different ways. The valuable points required for the enlightenment of the analysis is highlighted in
this section.
H.k.Jung [2] performed the experimental work in the induction heating process of A356 (ALTHIX) alloy billets of 76
mm diameter and 90 mm length to reduce the temperature gradient of the billet. The optimal reheating conditions to
apply the thixoforming process were investigated by changing the reheating time, holding time, holding temperatures,
capacity of the induction heating system, and adiabatic material size. This study shows that, the larger the billetsize, the
better the multi-step reheating, and the heating time and the capacity of the induction heating system must be increased.
In case of the three-step reheating process, the final holding time is most important factor and 2 min is suitable to
maintain a globular microstructure.
Dae-Cheol Ko et al [3] established an analytical technique in order to investigate the behaviour of semi-solid material
considering induction heating of the workpiece. The induction heating process isanalysed using the commercial finite
element software, ANSYS. The finite element program, SFAC2D, for the simulation of deformation in the semi-solid
state was developed. The behaviour of semi-solid material is described by a viscoplastic model for the solid phase and
by Darcy's law for the liquid flow. Simple compression and closed-die compression processes considering induction
heating are analysed. To validate the effectiveness of the proposed analytical technique, the results of simulation were
compared with those of experiment. [4]
Y. Favennec et al. [5] developed a general automatic optimization procedure coupled to a finite element induction
heating process simulation. The mathematical model and the numerical methods are presented along with results
validating the model. The first part of this paper presents the direct induction heating mathematical model, the related
main numerical choices and especially the ultra-weak coupling procedure. The general optimization problem is then
presented with the full detailed transposition of the ultra-weak coupling procedure to the adjoin problem. Numerical
results provided at the end prove the efficiency and robustness of the adjoin model in optimizing induction heating
processes.
Ki Wan Kim et al. [6] performed an inverse boundary analysis of surface radiation in an axisymmetric cylindrical
enclosure is conducted in this study. The net energy exchange method was used to calculate the radioactive heat flux on
each surface, and a hybrid genetic algorithm was adopted to minimize an objective function, which is expressed by the
sum of square errors between estimated and measured or desired heat fluxes on the design surface. They have examined
the effects on the estimation accuracy of the measurement error as well as the number of measurement points.
Furthermore, the effect of a variation in one boundary condition on the other boundary conditions was also investigated
to get the same desired heat flux and temperature distribution on the design surface.
Vivek R. Gandhewarl et al. [7] developed a new generation of industrial induction melting furnaces. The practices
followed in Induction Furnaces for the development are discussed in this paper. They carried out thorough a literature
review account of various practices presently being followed in steel industries using Induction Furnace with a view to
gather principal of working. They performed a pilot in few industries in India as well. They have provided some
recommendations for the productivity improvement. They proposed that due to non-availability of the proper
instrumentations the effect of the ill practices cannot be precisely judged, if this is properly measured, the percentage of
productivity improvement in steel melting Induction Furnace can be calculated.
A.Bhatt et al. [8] showed how to solve the induction heating problem in the induction furnace with complex geometry.
The results of this study have shown that the temperature of the crucible rises to 1500oC in 2 hours of heating time at
frequency of 8 kHz and current of 400 A. Hence these conditions are favourable for melting of copper (melting point =
1085 °C) in the crucible. The studies revealed that copper-liner is effective in reducing the electromagnetic coupling
between the coil and the vessel and thus prevents vessel from getting heated up by this effect.
It is observed from the literature that the FEM was primarily used in analysing the heat transfer in the induction furnace.
The literatures has not analysed an induction furnace in detailed way to fully develop a formulation for the thickness of
the composite wall and the applications of the literatures were oriented in the general rather a particular induction
furnace with constraints. The formulation of FEM was decided for the heat transfer analysis of induction furnace and
the simulation will be performed for the validation of the recently modified composite wall thickness.

ISSN: 2319-8753
II. THERMAL MODELLING OF INDUCTION PROCESS
A. Governing Equation –
The heat transfer analysis of the induction furnace is governed by the thermal diffusion equation in cylindrical form
and it is given by equation (1) .
T


 





1
R R s 
t
C
T
R
kR


(1)
Where s C is the specific heat capacity of the wall material,  is the density of the wall material, and R, θ and Z are
cylindrical coordinates[8].
Fig.2 Domain of the Induction furnace
B. Boundary Conditions:
1. On τ1, τ2, τ5, τ6, τ7
0
1

 


T

R


R 
R
kR
2. On τ3,
w q
T
R
kR
1 
R R

 





3. On τ4,
  o h T T
T
R
kR
1 
R R

  





Where w q
is given by,
2
I Lt
(1/ 2)

Ar
qw

ISSN: 2319-8753
 
o r
l
2
N A
L

Fig.2 shows the domain considered for the analysis and in this work, the domain is symmetric about the axis hence the
axis symmetric condition has been taken for the purpose of the analysis and to reduce the complexity in the
computation. The composite wall is consisting of ramming mass, mica, sintering cylinder and ceramic wall. The
boundary conditions considered for the calculation is shown above. The axis symmetric condition is applied along the
axis and boundary along τ1 is considered as insulated i.e. There is no heat exchange across the boundaries τ1, τ2, τ5,
τ6 and τ7. The coil is rounded around the boundaries τ3, τ4 and hence the heat flux is entering through it. The heat flux
condition has been depicted in the boundary condition across those boundaries [9-12].
The heat flux calculation is governed by the induction of the coil. The inductance of the coil is required in the calculation
of the heat flux input. For the present study the parameters of the furnace used in the industries has been adopted for the
calculations. The coil is having 15 numbers of turns around the furnace. The permeability and cross section of the coil
determines the inductance. The amount of the heat flux enters through the composite wall is greatly governed by the
different combinations of the composite wall thickness as well. The diameter of the furnace is about 600 mm and the
calculations have shown that the 15000 W/m2 amount of heat flux acts on the furnace.
C. Thermal stress
The thermal stressdistribution is calculated by determining the temperature distribution from the thermal analysis. In this,
the materials which are less in temperature will be reluctant for the expansion and hence prevents the expansion of the
layers of material with higher temperature. This restrictions induces the stress in the material of the induction furnace.
The different layers of the induction furnace wall having different materials results in the different thermal coefficient of
expansion. The variance of thermal expansion also induces the thermal stress. In ANSYS the input properties of the
materials will be used for the calculation of the thermal stress [13-15].
D. Simulation of Induction Process
Fig.2 shows the 3-D CAD model developed in Pro-E. The model was developed according to the present induction
furnace dimensions. The boundary conditions are applied based on the working condition for the purpose of simulation.
Figure 3. Thermal model of the induction furnace without the ceramic wall and with induction coil
The simulation will be performed in ANSYS and the parametric analysis will be performed for different composite wall
thickness with heat transfer between the wall by measuring the temperature across it. The input taken for the simulation
is shown in the Table.1. The simulation of induction furnace for the melting of the brass metal is typically a 2-phase
problem which needs more attention towards the melting of brass metal into liquid phase. But for the present work the
two-phase problem is converted into single phase considering only the metal remaining in the chamber which needs to be
melted. It is assumed that the metal after melting goes and settles down and provides convective boundary to the present
solid phase metal. The present work is interested in determining the amount of heat required for the melting of the entire
brass metal for the different combination of thickness of the composite wall and neglecting the temperature distribution
within the liquid phase of the metal [16-20].

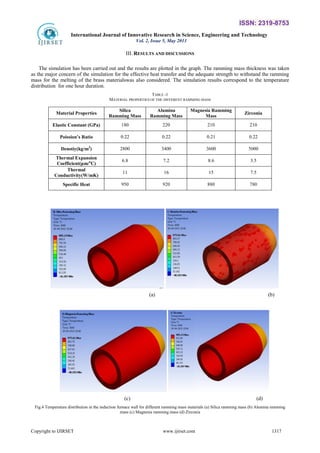
ISSN: 2319-8753
III. RESULTS AND DISCUSSIONS
The simulation has been carried out and the results are plotted in the graph. The ramming mass thickness was taken
as the major concern of the simulation for the effective heat transfer and the adequate strength to withstand the ramming
mass for the melting of the brass materialswas also considered. The simulation results correspond to the temperature
distribution for one hour duration.
TABLE -1
MATERIAL PROPERTIES OF THE DIFFERENT RAMMING MASS
Material Properties
Silica
Ramming Mass
Alumina
Ramming Mass
Magnesia Ramming
Mass
Zirconia
Elastic Constant (GPa) 180 220 210 210
Poission’s Ratio 0.22 0.22 0.21 0.22
Denstiy(kg/m3) 2800 3400 3600 5000
Thermal Expansion
Coefficient(μm/oC)
6.8 7.2 8.6 3.5
Thermal
Conductivity(W/mK)
11 16 15 7.5
Specific Heat 950 920 880 780
(a) (b)
(c) (d)
Fig.4 Temperature distribution in the induction furnace wall for different ramming mass materials (a) Silica ramming mass (b) Alumina ramming
mass (c) Magnesia ramming mass (d) Zirconia

ISSN: 2319-8753
The result of simulation for different materials having same wall thickness (75 mm) is shown in the Fig. 4. The
maximum temperatures reached in all the cases are dependent on thermal properties of the materials. It is observed that
the silica which is having thermal conductivity relatively lesser than other materials still produces the better inner wall
temperature as it is due to the fact that temperature distribution don’t depend only on thermal conductivity but also on
density of the material. The density as well resists the transfer of heat so it is obvious that the proper combination of
density and thermal conductivity has to be taken care for the wall material. The objective of the simulation also includes
the validation of wall thickness for the analysis. The present wall thickness (75 mm) produces reasonable results but still
it is required to verify dimensions of the wall thickness and need to validated the thickness of the wall by comparing the
results of simulation in different others thickness. The results of the analysis are shown in the Fig.5. The simulation
result of silica is shown in Fig.5 (b) as it gives better temperature distribution; it is taken for the further simulation
process.
Fig.5(a) shows that the reduction in the silica ramming mass thickness makes the heat transfer to increase so temperature
goes up for lesser thickness. The graph favours to have lesser and lesser thickness of the silica ramming mass so that the
heat transfer will be effective but together with the heat transfer, the strength criteria also required to be verified for the
validity of the design.
Fig.5 (b) shows the effectiveness of different ramming masses for the heat transfer. The thermal conductivity can be
increased by adding suitable ingredient and also by altering the composition of the ramming mass. For the present study,
silica ramming mass,alumina ramming mass, magnesiaramming mass and Zirconia were taken and their properties are
given in the Table 1 The graph plotted shows the temperature dependency on both density and thermal conductivity.
Silica ramming mass produces a maximum temperature of about 1537.6 K for the wall thickness 60 mm.The graph
shows the silica ramming mass has highest temperature for the same input among other materialsand it is also easily
available.
(a) (b)
Fig.5 Plot of Temperature of the inner wall (a) conductivity of ramming mass (b) Thickness of Ramming mass
IV. CONCLUSION
The analysis has been carried out for the effective heat transfer of the induction process. Theresults show the
effectiveness of ramming mass in the melting process. It plays an important role in the process. The simulation
performed shows the proper thickness and conductivity of it would enhance the melting and optimizes the heat process.
The result also highlights the application of FEM in the computation calculations of induction process. The FEM serves
better in providing the results with adequate accuracy. The further analysis has to be extended for the time dependent
input loading of the furnace which will reveal the fatigue related behavior of the furnace.
ACKNOWLEDGMENT
The author would like to thank department of mechanical engineering, school of engineering, RK University Rajkot,
for extending the facilities for the research work.
REFERENCES
[1] A. O¨zel, V. Ucar, A. MimarogluU, I. Calli “Comparison of the thermal stresses developed in diamond and advanced ceramic coating systems
under thermal loading” Materials and Design, Vol. 21,pp. 437-440, 2000.
[2] H.K. Jung, “The induction heating process of semi-solid aluminum alloys for thixoforming and their microstructure evaluation”, Journal of
Materials Processing Technology,Vol . 105,pp.176-190,2000.

ISSN: 2319-8753
[3] Dae-Cheol Ko, Gyu-Sik Min, Byung-Min Kim, Jae-Chan Choi, “Finite element analysis for the semi-solid state forming of aluminum alloy
considering induction heating”, Journal of Materials Processing Technology, Vol.100, pp. 95-104, 2000
[4] L.P. Borrego , J.M. Ferreira , J.M. Pinho da Cruz ,J.M. Costa, “ Evaluation of overload effects on fatigue crack growth and closure”,
Engineering Fracture Mechanics,Vol. 70,pp.1379–1397, 2003.
[5] Y. Favennec , V. Labbe, F. Bay, “Induction heating processes optimization a general optimal control approach”, Journal of Computational
Physics, Vol.187, pp.68–94,2003.
[6] Ki Wan Kim and Seung Wook Baek, “Inverse Surface Radiation Analysis In An Axisymmetric Cylindrical Enclosure Using A Hybrid Genetic
Algorithm”, Numerical Heat Transfer, Part A,Vol.46,pp.367–381, 2004.
[7] Vivek R. Gandhewar, Satish V. Bansod, Atul B.Borade, “Induction Furnace - A Review”, International Journal of Engineering and
Technology, Vol.3, pp.277-284,2011
[8] A. A. Bhat, S. Agarwal, D. Sujish, B. Muralidharan, B.P. Reddy, G.Padmakumar and K.K.Rajan , “ Thermal Analysis of Induction Furnace”,
proceedings of the COMSOL Bangalore 2012.
[9] M. Ben Salah, F. Askri, K. Slimi, S. Ben Nasrallah, “ Numerical resolution of the radiative transfer equation in a cylindrical enclosure with the
finite-volume method” International Journal of Heat and Mass Transfer Vol.47, pp.2501–2509. 2004
[10] Ozkan Sarikaya, Yasar Islamoglu, Erdal Celik, “Finite element modelling of the effect of the ceramic coating on heat transfer characteristics in
thermal barrier applications” Materials and Design Vol.26,pp.357–362,2005.
[11] Man Young Kim, Seung Wook Baek, “Modeling of radiative heat transfer in an axisymmetric cylindrical enclosure with participating
medium”, Journal of Quantitative Spectroscopy & Radiative Transfer Vol.090, pp.377–388,2005.
[12] J.C.Chai and Parth “Discrete-Ordinates and Finite-Volume Methods for Radiation Heat Transfer”, Treatment of Thermal Radiation in Heat
Transfer Problems, IIT Guwahati jan2-3, 2006.
[13] Man Young Kim “Assessment of the axisymmetric radiative heat transfer in a cylindrical enclosure with the finite volume method”
International Journal of Heat and Mass Transfer Vol.51,pp.5144–5153. ,2008.
[14] Joel J. Schubbe, “Evaluation of fatigue life and crack growth rates in 7050-T7451 aluminum plate for T-L and L-S oriented failure under
truncated spectra loading”, Engineering Failure Analysis Vol.16, pp.340–349,2009.
[15] Subhash C. Mishra, Man Young Kim, Ranjan Das, M. Ajith, and R. Uppaluri “Lattice Boltzmann Method Applied to the Analysis of Transient
Conduction radiation Problems in a Cylindrical Medium “Numerical Heat Transfer, Part A, Vol.56,pp.42–59, 2009.
[16] Raoudha Chaabane, Faouzi Askri, Sassi Ben Nasrallah,” Transient Combined Conduction and Radiation in a Two-Dimensional Participating
Cylinder in Presence of Heat Generation”, World Academy of Science, Engineering and Technology 55, 2011.
[17] Subhash C. Mishra, Man Young Kim, “Analysis Of Conduction And Radiation Heat Transfer In A 2-D Cylindrical Medium Using The
Modified Discrete Ordinate Method And The Lattice Boltzmann Method” Numerical Heat Transfer, Part A, Vol.60,pp.254–287, 2011.
[18] N.A. Kadhim, S. Abdullah, A.K. Ariffin , “Effective strain damage model associated with finite element modeling and experimental validation”
International Journal of Fatigue Vol.36 pp.194–205,2012
[19] Vital LeDez n, Hamou Sadat, “Radiative transfer in a semi-transparent medium enclosed in a cylindrical annulus” Journal of Quantitative
Spectroscopy & Radiative Transfer,Vol.113,pp. 96–116,2012.
[20] Sudhakar Matle, S.Sundar, “Axi-symmetric 2D simulation and numerical heat transfer characteristics for the calibration furnace in a rectangular
enclosure” Applied Mathematical Modelling, Vol 36,pp.878–893,2012
[21] JN Reddy, An Introduction to the Finite Element Method (Engineering Series) McGraw-Hill Science/Engineering/Math; 3 editions.
[22] Daryl Logan, “A First Course in he Finite Element Method”, 4th Edition, Cengage Learning, 2007.

3 finite

More Related Content

3 finite