ACCESS.2020.3015966.pdf

This work is licensed under a Creative Commons Attribution 4.0 License. For more information, see https://creativecommons.org/licenses/by/4.0/.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/ACCESS.2020.3015966, IEEE Access
VOLUME XX, 2017 1
Date of publication xxxx 00, 0000, date of current version xxxx 00, 0000.
Digital Object Identifier 10.1109/ACCESS.2017.Doi Number
Predicting stock market trends using machine
learning and deep learning algorithms via
continuous and binary data; a comparative
analysis on the Tehran stock exchange
Mojtaba Nabipour 1
, Pooyan Nayyeri 2
, Hamed Jabani 3
, Shahab S. 4
, Amir Mosavi 5*
1
Faculty of Mechanical Engineering, Tarbiat Modares University, Tehran, Iran, Mojtaba.nabipour@modares.ac.ir
2
School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran, pnnayyeri@ut.ac.ir
3
Department of Economics, Payame Noor University, West Tehran Branch, Tehran, Iran, h.jabani@gmail.com
4
Institute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam
5
Kalman Kando Faculty of Electrical Engineering, Obuda University, 1034 Budapest, Hungary
Corresponding author: Amir Mosavi (e-mail: amir.mosavi@kvk.uni-obuda.hu), Shahab S. (shamshirbandshahaboddin@duytan.edu.vn)
ABSTRACT The nature of stock market movement has always been ambiguous for investors because of
various influential factors. This study aims to significantly reduce the risk of trend prediction with machine
learning and deep learning algorithms. Four stock market groups, namely diversified financials, petroleum,
non-metallic minerals and basic metals from Tehran stock exchange, are chosen for experimental
evaluations. This study compares nine machine learning models (Decision Tree, Random Forest, Adaptive
Boosting (Adaboost), eXtreme Gradient Boosting (XGBoost), Support Vector Classifier (SVC), Naïve
Bayes, K-Nearest Neighbors (KNN), Logistic Regression and Artificial Neural Network (ANN)) and two
powerful deep learning methods (Recurrent Neural Network (RNN) and Long short-term memory (LSTM).
Ten technical indicators from ten years of historical data are our input values, and two ways are supposed
for employing them. Firstly, calculating the indicators by stock trading values as continues data, and
secondly converting indicators to binary data before using. Each prediction model is evaluated by three
metrics based on the input ways. The evaluation results indicate that for the continues data, RNN and
LSTM outperform other prediction models with a considerable difference. Also, results show that in the
binary data evaluation, those deep learning methods are the best; however, the difference becomes less
because of the noticeable improvement of models’ performance in the second way.
KEYWORDS Stock market, Trends prediction, Classification, Machine learning, Deep learning
I. INTRODUCTION
The task of stock prediction has always been a challenging
problem for statistics experts and finance. The main reason
behind this prediction is buying stocks that are likely to
increase in price and then selling stocks that are probably to
fall. Generally, there are two ways for stock market
prediction. Fundamental analysis is one of them and relies on
a company’s technique and fundamental information like
market position, expenses and annual growth rates. The
second one is the technical analysis method, which
concentrates on previous stock prices and values. This
analysis uses historical charts and patterns to predict future
prices [1&2].
Stock markets were normally predicted by financial experts
in the past time. However, data scientists have started solving
prediction problems with the progress of learning techniques.
Also, computer scientists have begun using machine learning
methods to improve the performance of prediction models
and enhance the accuracy of predictions. Employing deep
learning was the next phase in improving prediction models
with better performance [3&4]. Stock market prediction is
full of challenges, and data scientists usually confront some
problems when they try to develop a predictive model.

VOLUME XX, 2017 1
Complexity and nonlinearity are two main challenges caused
by the instability of stock market and the correlation between
investment psychology and market behavior [5].
It is clear that there are always unpredictable factors such as
the public image of companies or political situation of
countries, which affect stock markets trend. Therefore, if the
data gained from stock values are efficiently preprocessed
and suitable algorithms are employed, the trend of stock
values and index can be predicted. In stock market prediction
systems, machine learning and deep learning approaches can
help investors and traders through their decisions.These
methods intend to automatically recognize and learn patterns
among big amounts of information. The algorithms can be
effectively self-learning, and can tackle the predicting task of
price fluctuations in order to improve trading strategies [6].
Since recent years, many methods have been improved to
predict stock market trends. The implementation of a model
combination with Genetic Algorithms (GA), Artificial Neural
Networks and Hidden Markov Model (HMM) was proposed
by Hassan et al. [7]; the purpose was transforming the daily
stock prices to independent sets of values as input to HMM.
The predictability of financial trend with SVM model by
evaluating the weekly trend of NIKKEI 225 index was
investigated by Huang et al. [8]. A comparison between
SVM, Linear Discriminant Analysis, Elman
Backpropagation Neural Networks and Quadratic
Discriminant Analysis was their goal. The results indicated
that SVM was the best classifier method. New financial
prediction algorithm based on SVM ensemble was proposed
by Sun et al. [9]. The method for choosing SVM ensemble’ s
base classifiers from candidate ones was proposed by
deeming both diversity analysis and individual performance.
Final results showed that SVM ensemble was importantly
better than individual SVM for classification. Ten data
mining methods were employed by Ou et al. [10] to predict
value trends of Hang index from Hong Kong stock market.
The methods involved Tree based classification, K-nearest
neighbor, Bayesian classification, SVM and neural network.
Results indicated that the SVM outperformed other
predictive models. The price fluctuation by a developed
Legendre neural network was forecasted by Liu et al. [11] by
assuming investors’ positions and their decisions by
analyzing the prior data on the stock values. They also
examined a random function (time strength) in the
forecasting model. Araújo et al. [12] proposed the
morphological rank linear forecasting approach to compare
its results with time-delay added evolutionary forecasting
approach and multilayer perceptron networks.
From the above research background, it is clear that each of
the algorithms can effectively solve stock prediction
problems. However, it is vital to notice that there are specific
limitations for each of them. The prediction results not only
are affected by the representation of the input data but also
depend on the prediction method. Moreover, using only
prominent features and identifying them as input data instead
of all features can noticeably develop the accuracy of the
prediction models.
Employing tree-based ensemble methods and deep learning
algorithms for predicting the stock and stock market trend is
a recent research activity. In light of employing bagging and
majority vote methods, Tsai et al. [13] used two different
kinds of ensemble classifiers, such as heterogeneous and
homogeneous methods. They also consider macroeconomic
features and financial ratios from Taiwan stock market to
examine the performance of models. The results
demonstrated that with respect to the investment returns and
prediction accuracy, ensemble classifiers were superior to
single classifiers. Ballings et al. [14] compared the
performance of AdaBoost, Random Forest and kernel factory
versus single models involving SVM, KNN, Logistic
Regression and ANN. They predict European company’s
prices for one-year ahead. The final results showed that
Random Forest outperformed among all models. Basak et al.
[15] employed XGBoost and Random Forest methods for the
classification problem to forecast the stock increase or
decrease based on previous values. Results showed that the
prediction performances have advanced for several
companies in comparison with the existing ones. For
examining macroeconomic indicators to accurately predict
stock market for one-month ahead, Weng et al. [16]
improved four ensemble models, boosting regressor, bagging
regressor, neural network ensemble regressor and random
forest regressor. Indeed, another aim was employing a hybrid
way of LSTM to prove that the macroeconomic features are
the most successful predictors for stock market.
Moving on using deep learning algorithms, Long et al. [17]
examined a deep neural network model with public market
data and the transaction records to evaluate stock price
movement. The experimental results showed that
bidirectional LSTM could predict the stock price for financial
decisions, and the method acquired the best performance
compared to other prediction models. Rekha et al. [18]
employed CNN and RNN to make a comparison between
two algorithms’ results and actual results via stock market
data. Pang et al. [19] tried to improve an advanced neural
network method to get better stock market predictions. They
proposed LSTM with an embedded layer and LSTM with an
automatic encoder to evaluate the stock market movement.
The results showed that the LSTM with embedded layer
outperformed and the models’ accuracy for the Shanghai
composite index is 57.2 and 56.9%, respectively. Kelotra and
Pandey [20] used the deep convolutional LSTM model as a
predictor to effectively examine stock market movements.
The model was trained with Rider-based monarch butterfly
optimization algorithm and they achieved a minimal MSE
and RMSE of 7.2487 and 2.6923. Baek and Kim [21]
proposed an approach for stock market index forecasting,
which included a prediction LSTM module and an overfitting
prevention LSTM module. The results confirmed that the
proposed model had an excellent forecasting accuracy

VOLUME XX, 2017 1
compared to model without an overfitting prevention LSTM
module. Chung and Shin [22] employed a hybrid approach of
LSTM and GA to improve a novel stock market prediction
model. The final results showed that the hybrid model of
LSTM network and GA was superior in comparison with the
benchmark model.
Overall, regarding the above literature, prior studies often
concentrated on macroeconomic or technical features with
recent machine learning methods to detect stock index or
values movement without considering appropriate
preprocessing methods.
Iran's stock market has been highly popular recently because
of arising growth of Tehran Price Index in the last decades,
and one of the reasons is that most of the state-owned firms
are being privatized under the general policies of article 44 in
the Iranian constitution, and people are allowed to buy the
shares of newly privatized firms under the specific
circumstances. This market has some specific attributes in
comparison with other country's stock markets, one of them
is dealing price limitation of ±5% of opening price of the day
for every indexes; this issue hinders the abnormal market
fluctuation and scatter market shocks, political issues, etc.
over specific time and could make the market smoother;
however, the effect of fundamental parameters on this market
is relatively high and the prediction task of future movements
is not simple.
This study concentrates on the process of future trends
prediction for stock market groups, which are crucial for
investors. Despite significant development in Iran stock
market in recent years, there has been not enough research on
the stock price predictions and movements using novel
machine learning methods.
In this paper, we concentrate on comparing prediction
performance of nine machine learning models (Decision
Tree, Random Forest, Adaboost, XGBoost, SVC, Naïve
Bayes, KNN, Logistic Regression and ANN) and two deep
learning methods (RNN and LSTM) to predict stock market
movement. Ten technical indicators are employed as input
values to our models. Our study includes two different
approaches for inputs, continues data and binary data, to
investigate the effect of preprocessing; the former uses stock
trading data (open, close, high and low values) while the
latter employs preprocessing step to convert continues data to
binary one. Each technical indicator has its specific
possibility of up or down movement based on market
inherent properties. The performance of the mentioned
models is compared for the both approaches with three
classification metrics, and the best tuning parameter for each
model (except Naïve Bayes and Logistic Regression) is
reported. All experimental tests are done with ten years of
historical data of four stock market groups (diversified
financials, petroleum, non-metallic minerals and basic
metals), which are completely crucial for investors, from
Tehran stock exchange. We believe that this study is a new
research paper that incorporates multiple machine learning
and deep learning methods to improve the prediction task of
stock groups’ trend and movement.
This paragraph is organized to show the structure of our
paper. Section 2 defines our research data with some
statistical data, and two approaches supposed for input
values. Eleven prediction models, including nine machine
learning and two deep learning algorithms, are introduced
and discussed in Section 3. The final results of prediction are
presented in Section 4 with analyzing, and Section 5
concludes our paper.
II. Research data
In this study, ten years of historical data of four stock market
groups (diversified financials, petroleum, non-metallic
minerals and basic metals) from November 2009 to
November 2019 is employed, and all data is gained from
www.tsetmc.com website. Figures 1-4 show the number of
increase or decrease cases for each group during ten years.
FIGURE 1. The number of increasing and decreasing cases (trading
days) in each year for the diversified financials group.
days) in each year for the petroleum group.

VOLUME XX, 2017 1
days) in each year for the diversified financials group.
days) in each year for the basic metals group
In the case of predicting stock market movement, there are
several technical indicators and each of them has a specific
ability to predict future trends of market; however, we choose
ten technical indicators in this paper based on previous
studies [23-25]. Table 1 (in Appendix section) shows
technical indicators and their formulas, and Table 2 (in
Appendix section) indicates summary statistics of the
indicators of four stock groups. The inputs for calculating
indicators are open, close, high and low values in each
trading day.
This paper involves two approaches for input information.
continues data is supposed to be based on actual time series,
and binary data is presented with a preprocessing step to
convert continues data to binary one with respect to each
indicator nature.
A. Continuous data
In this method, input values to prediction models are
computed from formulas in Table 1 for each technical
indicator. The indicators are normalized in the range of (0,
+1) before using to prevent overwhelming smaller values by
larger ones. Figure 5 shows the process of stock trend
prediction with continues data.
FIGURE 5. Predicting stock movement with continuous data.
B. Binary data
In this approach, a new step is added to convert continuous
values of indicators to binary data based on each indicator’s
nature and property. Figure 6 indicates the process of stock
trend prediction with binary data. Here, binary data is
introduced by +1 as the sign of upward trend and -1 as the
sign of downward trend.
FIGURE 6. Predicting stock movement with binary data
Details about the way of calculating indicators are presented
here [25-27]:
SMA is calculated by the average of prices in a selected
range, and this indicator can help to determine if a price will
continue its trend. WMA gives us a weighted average of the
last n values, where the weighting falls with each prior price.
• SMA and WMA: if current value is below the
moving average then the trend is -1, and if current
value is above the moving average then the trend is
+1.
MOM calculates the speed of the rise or falls in stock prices
and it is a very useful indicator of weakness or strength in
evaluating prices.

VOLUME XX, 2017 1
• MOM: if the value of MOM is positive then the
trend is +1, otherwise it is -1.
STCK is a momentum indicator over a particular period of
time to compare a certain closing price of a stock to its price
range. The oscillator sensitivity to market trends can be
reduced by modifying that time period or by a moving
average of results. STCD measures the relative position of
the closing prices in comparison with the amplitude of price
oscillations in a certain period. This indicator is based on the
assumption that as prices increase, the closing price tends
towards the values which belong to the upper part of the area
of price movements in the preceding period and when prices
decrease, the opposite is correct. LWR is a type of
momentum indicator which evaluates oversold and
overbought levels. Sometimes LWR is used to find exit and
entry times in the stock market. MACD is another type of
momentum indicator which indicates the relationship
between two moving averages of a share’s price. Traders
usually can use it to buy the stock when the MACD crosses
above its signal line and sell the shares when the MACD
crosses below the signal line. ADO is usually used to find out
the flow of money into or out of stock. ADO line is normally
employed by traders seeking to determine buying or selling
time of stock or verify the strength of a trend.
• STCK, STCD, LWR, MACD and ADO: if the
current value (time t) is more than the previous
value (time t-1) then the trend is +1, otherwise it is -
1.
RSI is a momentum indicator that evaluates the magnitude of
recent value changes to assess oversold or overbought
conditions for stock prices. RSI is showed as an oscillator (a
line graph which moves between two extremes) and moves
between 0 to 100.
• RSI: its value is between 0 and 100. If the RSI value
surpasses 70 then the trend is -1, and if the value
goes below 30 then the trend is +1. For values
between 30 and 70, if the current value (time t) is
larger than the prior value (time t-1) then the trend
is +1, otherwise it is -1.
CCI is employed as a momentum-based oscillator to
determine when a stock price is reaching a condition of being
oversold or overbought. CCI also measures the difference
between the historical average price and the current price.
The indicator determines the time of entry or exit for traders
by providing trade signals.
• CCI: if values surpass 200 then the trend is -1 and if
values go below -200 then the trend is +1. For
values between -200 and 200, if the current value
(time t) is larger than the prior value (time t-1) then
the trend is +1, otherwise it is -1.
III. Prediction models
In this study, we use nine machine learning methods
(Decision Tree, Random Forest, Adaboost, XGBoost, SVC,
Naïve Bayes, KNN, Logistic Regression and ANN) and two
deep learning algorithms (RNN and LSTM).
A. Decision Tree
Decision Tree is a popular supervised learning approach
employed for both regression and classification problems.
The purpose is to make a model which is able to predict a
target value by learning easy decision rules formed from the
data features. There are some advantages of using this
method like being easy to interpret and understand or Able to
work out problems with multi-outputs; in contrast, creating
over-complex trees that results in overfitting is a common
disadvantage. A schematic illustration of Decision Tree is
shown in Figure 7.
FIGURE 7. Schematic illustration of Decision tree
B. Random Forest
Great number of decision trees make a random forest model.
The method simply averages the prediction result of trees,
which is called a forest. Also, this model has three random
concepts, randomly choosing training data when making
trees, selecting some subsets of features when splitting nodes
and considering only a subset of all features for splitting each
node in each simple decision tree. During training data in a
random forest, each tree learns from a random sample of the
data points. A schematic illustration of Random forest is
indicated in Figure 8.

VOLUME XX, 2017 1
FIGURE 8. Schematic illustration of Random forest
C. Adaboost
Boosting methods are a group of algorithms which convert
weak learners to a powerful learner. The method is an
ensemble for improving the model predictions of any
learning algorithm. The concept of boosting is to sequentially
train weak learners in order to modify their past prediction.
AdaBoost is a meta-estimator which starts by fitting a model
on the main dataset before fitting additional copies of the
model on the similar dataset. During the process, samples’
weights are adapted based on the current prediction error, so
the subsequent model concentrates more on difficult items.
D. XGBoost
XGBoost is an ensemble tree-based method, and the model
applies the principle of boosting for weak learners. XGBoost
was introduced for better speed and performance in
comparison with other tree-bassed models. In-built cross-
validation ability, regularization for avoiding overfitting,
efficient handling of missing data, catch awareness, tree
pruning and parallelized tree building are common
advantages of XGBoost method.
E. SVC
Support Vector Machines (SVMs) are a set of supervised
learning approaches that can be employed for classification
and regression problems. The classifier version is named
SVC. The method’s purpose is finding a decision boundary
between two classes with vectors. The boundary must be far
from any point in the dataset, and support vectors are the sign
of observation coordinates with a gap named margin. SVM is
a boundary that best separates two classes with employing a
line or hyperplane. The decision boundary is defined in
Equation 1 where SVMs can map input vectors xi ϵ Rd
into a
high dimensional feature space Ф(xi) ϵ H, and Ф(.) is mapped
by a kernel function K(xi, xj). Figure 9 shows the schematic
illustration of SVM method.
1
( ) sgn( . ( , ) )
n
i i i
i
f x y K x x b

=
= +
 (1)
FIGURE 9. Schematic illustration of SVM
SVMs can perform a linear or non-linear classification
efficiently, but for non-linear, they must use a kernel trick
which map inputs to high-dimensional feature spaces. SVMs
convert non-separable classes to separable ones by kernel
functions such as linear, non-linear, sigmoid, radial basis
function (RBF) and polynomial. The formula of kernel
functions is shown in Equations 2-4 where γ is the constant
of radial basis function and d is the degree of polynomial
function. Indeed, there are two adjustable parameters in the
sigmoid function, the slope α and the intercepted constant c.
)
exp(
)
,
(
:
2
j
i
j
i x
x
x
x
K
RBF −
−
=  (2)
d
j
i
j
i x
x
x
x
K
Polynomial )
1
.
(
)
,
(
: +
= (3)
: ( , ) tanh( )
T
i j i
Sigmoid K x x x y c

= + (4)
SVMs are often effective in high dimensional spaces and
cases where the number of dimensions is greater than the
number of samples, but to avoid over-fitting in selecting
regularization term and kernel functions, the number of
features should be much greater than the number of samples.
F. Naïve Bayes
Naïve Bayes classifier is a member of probabilistic classifiers
based on Bayes' theorem with strong independence
assumptions between the features given the value of the class
variable. This method is a set of supervised learning
algorithms. The following relationship is stated in Equation 5
by Bayes’ theorem where y is class variable, and x1 through
xn are dependent feature vectors.

VOLUME XX, 2017 1
1
1
( ) ( )
( ,..., )
1
( ,..., )
n
i
i
n
P y P x y
P x x
n
P y x x =

= (5)
Naive Bayes classifier can be highly fast in comparison with
more sophisticated algorithms. The separation of the class
distributions means that each one can be independently
evaluated as a one-dimensional distribution. This in turn
helps for alleviating problems from the dimensionality curse.
G. KNN
Two properties usually are suggested for KNN, lazy learning
and non-parametric algorithm, because there is not any
assumption for underlying data distribution by KNN. The
method follows some steps to find targets: Dividing dataset
into training and test data, selecting the value of K,
determining which distance function should be used,
choosing a sample from test data (as a new sample) and
computing the distance to its n training samples, sorting
distances gained and taking k-nearest data samples, and
finally, assigning the test class to the sample on the majority
vote of its k neighbors. Figure 10 shows the schematic
illustration of KNN method.
FIGURE 10. Schematic illustration of KNN
H. Logistic Regression
Logistic regression is used to assign observations to a
separated set of classes as a classifier. The algorithm
transforms its output to return a probability value with the
logistic sigmoid function, and predicts the target by the
concept of probability. Logistic Regression is similar to
Linear Regression model, but the Logistic Regression
employs sigmoid function, instead of logistic one, with more
complexity. The hypothesis behind logistic regression tries to
limit the cost function between 0 and 1.
I. ANN
ANNs are single or multi-layer neural nets which fully
connected together. Figure 11 shows a sample of ANN with
an input and output layer and also two hidden layers. In a
layer, each node is connected to every other node in the next
layer. By the rise in the number of hidden layers, it is
possible to make the network deeper.
FIGURE 11. Schematic illustration of ANN
Figure 12 is indicated for each of the hidden or output nodes,
while a node takes the weighted sum of the inputs, added to a
bias value, and passes it through an activation function
(usually a non-linear function). The result is the output of the
node that becomes another node input for the next layer. The
procedure moves from the input to the output, and the final
output is determined by doing this process for all nodes.
Learning process of weights and biases associated with all
nodes for training the neural network.
FIGURE 12. An illustration of relationship between inputs and output
for ANN.

VOLUME XX, 2017 1
Equation 6 shows the relationship between nodes, weights
and biases. The weighted sum of inputs for a layer passed
through a non-linear activation function to another node in
the next layer. It can be interpreted as a vector, where X1, X2
… and Xn are inputs, w1, w2, … and wn are weights
respectively, n is the number of inputs for the final node, f is
activation function and z is the output.
1
( . ) ( )
n
i i
i
Z f x w b f x w b
=
= + = +
 (6)
By calculating weights and biases, the training process is
completed by some rules: initialize the weights and biases for
all the nodes randomly, performing a forward pass by the
current weights and biases, calculating each node output,
comparing the final output with the actual target, and
modifying the weights/biases consequently by gradient
descent with the backward pass, generally known as
backpropagation algorithm.
J. RNN
A very prominent version of neural networks is recognized as
RNN which is extensively used in various processes. In a
normal neural network, the input is processed through a
number of layers and an output is made. It is proposed that
two consecutive inputs are independent of each other.
However, the situation is not correct in all processes. For
example, for the prediction of stock market at a certain time,
it is crucial to consider the previous observations.
RNN is named recurrent due to it does the same task for each
item of a sequence when the output is related to the previous
computed values. As another important point, RNN has a
specific memory, which stores previous computed
information for a long time. In theory, RNN can use
information randomly for long sequences, but in real
practices, there is a limitation to look back just a few steps.
Figure 13 shows the architecture of RNN.
FIGURE 13. An illustration of recurrent network
K. LSTM
LSTM is a specific kind of RNN with a wide range of
applications like time series analysis, document
classification, voice and speech recognition. In contrast with
feedforward ANNs, the predictions made by RNNs are
dependent on previous estimations. In real, RNNs are not
employed extensively because they have a few deficiencies
which cause impractical evaluations.
Without investigation of too much detail, LSTM solves the
problems by employing assigned gates for forgetting old
information and learning new ones. LSTM layer is made of
four neural network layers that interact in a specific method.
A usual LSTM unit involves three different parts, a cell, an
output gate and a forget gate. The main task of cell is
recognizing values over random time intervals and the task of
controlling the information flow into the cell and out of it
belongs to the gates.
L. Models’ parameters
Since stock market data are time-series information, there are
two approaches for training dataset of prediction models.
Because of the recurrent nature of RNN and LSTM models,
the technical indicators of one or more days (up to 30 days)
are considered and rearranged as input data to be fed into the
models. For other models except RNN and LSTM, ten
technical indicators are fed to the model. Output of all
models is the stock trend value with respect to input data. For
recurrent models, output is the stock trend value of the last
day of the training sample.
All models (except Naïve Bayes) have one or several
parameters known as hyper-parameters which should be
adjusted to obtain optimal results. In this paper, one or two
parameters of every model (except Decision Tree and
Logistic Regression which fixed parameter(s) is used) is
selected to be adjusted for an optimal result based on

VOLUME XX, 2017 1
numerous experimental works. In Tables 3-5, all fixed and
variable parameters of tree-based models, traditional
supervised models, and neural-network-based models are
presented, respectively.
TABLE 3
TREE-BASED MODELS PARAMETERS
Model Parameters Value(s)
Decision Tree Max Depth 10
Bagging Classifier Max Depth 10
Estimator Decision Tree
Number of Trees 50, 100, 150, … , 500
Random Forest Max Depth 10
Number of Trees 50, 100, 150, … , 500
Adaboost Max Depth 10
Estimator Decision Tree
Number of Trees 50, 100, 150, … , 500
Learning Rate 0.1
Gradient Boosting Max Depth 10
Number of Trees 50, 100, 150, … , 500
Learning Rate 0.1
XGBoost Max Depth 10
Number of Trees 50, 100, 150, … , 500
Objective Logistic Regression for
Binary Classification
TABLE 4
TRADITIONAL SUPERVISED MODELS PARAMETERS
Model Parameters Value(s)
SVC Kernels Linear, Poly (degree = 3), RBF,
Sigmoid
Naïve Bayes C 1.0
Gamma 1/(numf×variancef)
f : features
Algorithm Gaussian
KNN Classifier Number of
Neighbors
1, 2, 3, … , 100
Algorithm K-dimensional Tree
Logistic
Regression
Weights Uniform
Leaf Size 30
Metric Euclidean Distance (L2)
Tolerance 10-4
Model C 1.0
Penalty Euclidean Distance (L2)
Parameters Value(s)
SVC Kernels Linear, Poly (degree = 3), RBF,
Sigmoid
C 1.0
Gamma 1/((num)f×(variance)f)
f : features
TABLE 5
ANN, RNN AND LSTM PARAMETERS
ANN Parameters
Parameters Value(s)
Hidden Layer Neuron
Count
20, 50, 100, 200, 500
Activation Function ReLU, Sigmoid, Tanh
Optimizer Adam:
learning rate = 0.001
β1=0.9, β2=0.999
Training Stop Condition Early stopping:
Monitoring parameter = validation
data accuracy
Patience = 100 epochs
Max Epochs 10000
RNN and LSTM Parameters
Parameters Value(s)
Hidden Layer Neuron
Count
500
Number of Training Days 1, 2, 5, 10, 20, 30
Neuron Type RNN/LSTM
Activation Function Tanh, Softmax
Optimizer Adam:
learning rate = 0.00005
β1=0.9, β2=0.999
Training Stop Condition Early stopping:
monitoring parameter = validation
data accuracy
patience = 100 epochs
Max Epochs 10000
IV. Experimental results
A. Classification metrics
F1-Score, Accuracy and Receiver Operating Characteristics-
Area Under the Curve (ROC-AUC) metrics are employed to
evaluate the performance of our models. For Computing F1-
score and Accuracy, Precision and Recall must be evaluated
by Positive (TP), True Negative (TN), False Positive (FP)
and False Negative (FN). These values are indicated in
Equations 7 and 8.
TP
Precision
TP FP
=
+ (7)
TP
Recall
TP FN
=
+ (8)
By calculation of above equations, F1-Score and Accuracy
are defined in Equations 9 and 10.
TP TN
Accuracy
TP FP TN FN
+
=
+ + + (9)
2 Pr Re
1
Pr Re
ecision call
F Score
ecision call
 
− =
+
(10
)
Among classification metrics, Accuracy is a good metric, but
it is not enough for all classification problems. It is often
necessary to look at some other metrics to make sure that a
model is reliable. F1-Score might be a better metric to
employ if results need to achieve a balance between Recall
and Precision, especially when there is an uneven class

VOLUME XX, 2017 1
distribution. ROC-AUC is another powerful metric for
classification problems, and is calculated based on the area
under ROC-AUC curve from prediction scores.
B. Results
For training machine learning models, we implement the
following steps: normalizing features (just for continues
data), randomly splitting the main dataset into train data and
test data (30% of dataset was assigned to the test part), fitting
the models and evaluating them by validation data (and
“early stopping”) to prevent overfitting, and using metrics for
final evaluation with test data. The creating deep models is
different from machine learning when the input values must
be three dimensional (samples, time_steps, features); so, we
use a function to reshape the input values. Also, weight
regularization and dropout layer are employed to prevent
overfitting here. All coding process in this study is
implemented by python3 with Scikit Learn and Kears library.
Based on extensive experimental works by deeming the
approaches, the following outcomes are obtained:
In the first approach, continuous data for the features is used,
and Tables 6-8 show the result of this method. For each
model, the prediction performance is evaluated by the three
metrics. Also, the best tuning parameter for all models
(except Naïve Bayes and Logistic Regression) is reported.
For achieving a better image of experimental works, Figure
14 is made to indicate the average of F1-score based on
average running time through the stock market groups. It can
be seen that Naive-Bayes and Decision Tree are least
accurate (approximately 68%) while RNN and LSTM are top
predictors (roughly 86%) with a considerable difference
compared to other models. Indeed, the running time of those
superiors is more than other algorithms.
In the second approach, binary data for the features is
employed, and Tables 9-11 demonstrate the result of this
way. The structure and experimental works here are similar
to the first approach except inputs where we use an extra
layer to convert continues data to binary one based on the
nature and property of the features. Similarly, for better
understanding, Figure 15 is made to show the average of F1-
score based on average running time through the stock
market groups. It is clear that there is a significant
improvement in the prediction performance of all models in
comparison with the first approach, and this achievement is
obviously shown in Figure 16. There is no change in the
inferior methods (Naive-Bayes and Decision Tree with
roughly 85% F1-score) and the superior predictors (RNN and
LSTM with approximately 90% F1-score), but the difference
between them becomes less by binary data. Also, the
prediction process for all models is faster in the second
approach.
TABLE 6
TREE-BASED MODELS WITH BEST PARAMETERS FOR CONTINUOUS DATA
Stock
Group
Prediction Model
Decision Tree Random Forest
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
Div.
Fin.
0.69
93
0.684
6
0.68
38
1
0.72
00
0.721
8
0.72
24
50
Metals
0.71
64
0.653
8
0.63
47
1
0.75
53
0.707
7
0.68
98
100
Miner
als
0.66
58
0.651
3
0.65
19
1
0.74
64
0.728
2
0.72
71
100
Petrole
um
0.64
59
0.664
1
0.66
32
1
0.70
42
0.730
8
0.72
88
250
Adaboost XGBoost
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
Div.
Fin.
0.72
66
0.723
1
0.72
05
250
0.72
13
0.716
7
0.71
67
100
Metals
0.75
53
0.705
1
0.69
04
250
0.75
77
0.706
4
0.69
06
150
Miner
als
0.72
77
0.706
4
0.70
46
100
0.71
96
0.701
3
0.70
05
50
Petrole
um
0.71
48
0.721
8
0.72
17
50
0.69
64
0.711
5
0.71
07
250
TABLE 7. SUPERVISED MODELS WITH BEST PARAMETERS FOR
CONTINUOUS DATA
Stock
Group
Prediction Model
SVC Naïve Bayes
F1-
score
Accura
cy
ROC
AUC
Kernel
F1-
score
Accura
cy
ROC
AUC
Div.
Fin.
0.73
12
0.7154 0.71
43
Poly
0.68
66
0.6782 0.67
80
Metals
0.78
33
0.7269 0.70
29
RBF
0.72
23
0.6846 0.68
19
Minera
ls
0.75
29
0.7282 0.72
48 Linear
0.66
58
0.6692 0.67
43
Petrole
um
0.69
17
0.7051 0.70
45
RBF
0.64
29
0.6795 0.67
71
KNN
Logistic Regression
F1-
score
Accura
cy
ROC
AUC Neighb
ors
F1-
score
Accura
cy
ROC
AUC
Div.
Fin.
0.72
44
0.7141 0.71
36
47
0.73
21
0.7167 0.71
36
Metals
0.78
59
0.7359 0.71
71 21
0.77
10
0.7167 0.69
65
Minera
ls
0.73
53
0.7167 0.74
15
41
0.75
29
0.7282 0.72
48
Petrole
um
0.69
29
0.7103 0.70
92
17
0.69
11
0.7077 0.70
67

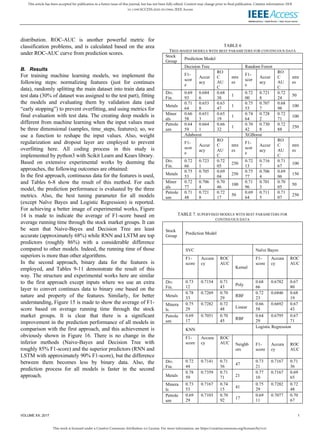
VOLUME XX, 2017 1
TABLE 8
NEURAL-NETWORK-BASED MODELS WITH BEST PARAMETERS FOR
CONTINUOUS DATA
Stock
Grou
p
Prediction Model
ANN
F1-
sco
re
Accu
racy
RO
C
AU
C
Activation Func./epochs
Div.
Fin.
0.7
590
0.75
00
0.7
495
ReLU/245
Metal
s
0.7
932
0.73
59
0.7
091
ReLU/90
Mine
rals
0.7
671
0.74
62
0.7
437
ReLU/233
Petro
leum
0.6
932
0.71
28
0.7
116
Tanh/148
RNN LSTM
F1-
sco
re
Accu
racy
RO
C
AU
C
ndays/e
pochs
F1-
sco
re
Accu
racy
RO
C
AU
C
ndays/e
pochs
Div.
Fin.
0.8
620
0.86
43
0.8
643
20/842
0.8
638
0.86
43
0.8
643
20/773
Metal
s
0.8
571
0.82
82
0.8
238
20/772
0.8
581
0.82
95
0.8
254
20/525
Mine
rals
0.8
810
0.87
16
0.8
702
5/398
0.8
798
0.87
16
0.8
709
5/402
Petro
leum
0.8
279
0.82
24
0.8
221
10/373
0.8
356
0.83
14
0.8
312
10/358
FIGURE 14. Average of F1-Score based on average logarithmic running
per sample for continues data
TABLE 9
TREE-BASED MODELS WITH BEST PARAMETERS FOR BINARY DATA
Stock
Group
Prediction Model
Decision Tree Random Forest
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
Div.
Fin.
0.84
21
0.846
2
0.84
60
1
0.85
08
0.853
8
0.85
38
450
Metals
0.87
38
0.847
4
0.83
64
1
0.87
94
0.851
3
0.83
60
400
Miner
als
0.86
60
0.866
7
0.86
68
1
0.86
71
0.867
9
0.86
80
100
Petrole
um
0.82
78
0.834
6
0.83
49
1
0.84
02
0.844
9
0.84
57
150
Adaboost XGBoost
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
F1-
scor
e
Accur
acy
RO
C
AU
C
ntre
es
Div.
Fin.
0.85
38
0.856
4
0.85
64
400
0.85
23
0.855
1
0.85
51
50
Metals
0.87
92
0.851
3
0.83
65
450
0.87
88
0.852
6
0.84
03
50
Miner
als
0.86
74
0.867
9
0.86
80
300
0.86
68
0.867
9
0.86
81
150
Petrole
um
0.84
13
0.846
2
0.84
70
50
0.84
07
0.843
6
0.84
51
100
TABLE 10
SUPERVISED MODELS WITH BEST PARAMETERS FOR BINARY DATA
Stock
Group
Prediction Model
SVC Naïve Bayes
F1-
score
Accura
cy
ROC
AUC Kernel
F1-
score
Accura
cy
ROC
AUC
Div.
Fin.
0.85
53
0.8590 0.85
88
Linear
0.83
51
0.8410 0.84
06
Metals
0.88
72
0.8679 0.86
45
Poly
0.84
66
0.8295 0.83
54
Minera
ls
0.87
21
0.8718 0.87
18
Linear
0.83
13
0.8372 0.83
75
Petrole
um
0.85
44
0.8641 0.86
30
Poly
0.83
27
0.8423 0.84
16
KNN Logistic Regression
F1-
score
Accura
cy
ROC
AUC
Neighb
ors
F1-
score
Accura
cy
ROC
AUC
Div.
Fin.
0.86
07
0.8551 0.85
63
13
0.85
26
0.8564 0.85
62
Metals
0.88
94
0.8641 0.85
02
60
0.88
37
0.8603 0.85
10
Minera
ls
0.86
49
0.8667 0.86
68
27
0.86
80
0.8667 0.86
66
Petrole
um
0.84
73
0.8526 0.85
32
21
0.85
32
0.8641 0.86
26
TABLE 11
NEURAL-NETWORK-BASED MODELS WITH BEST PARAMETERS FOR BINARY
DATA
Stock
Grou
p
Prediction Model
ANN
F1-
sco
re
Accu
racy
RO
C
AU
C
Activation Func./epochs
Div.
Fin.
0.8
691
0.87
56
0.8
750
Sigmoid/111
Metal
s
0.8
925
0.87
18
0.8
645
Tanh/6
Mine
rals
0.8
733
0.87
05
0.8
704
Tanh/305
Petro
leum
0.8
646
0.87
31
0.8
722
ReLU/19
RNN LSTM
F1-
sco
re
Accu
racy
RO
C
AU
C
ndays/e
pochs
F1-
sco
re
Accu
racy
RO
C
AU
C
ndays/e
pochs
Div.
Fin.
0.9
024
0.90
12
0.9
016
5/68
0.8
994
0.89
86
0.8
991
5/61
Metal 0.9 0.88 0.8 5/233 0.9 0.88 0.8 5/252

VOLUME XX, 2017 1
s 011 19 727 017 19 714
Mine
rals
0.8
943
0.88
97
0.8
895
2/284
0.8
900
0.88
46
0.8
842
2/143
Petro
leum
0.8
852
0.89
36
0.8
923
2/115
0.8
828
0.89
10
0.8
899
2/152
FIGURE 15. Average of F1-Score based on average logarithmic running
per sample for binary data.
FIGURE 16. The average of F1-Score with continuous and binary data
for all models.
As a prominent result, deep learning methods (RNN and
LSTM) show a powerful ability to predict stock movement in
both approaches, especially for continues data when the
performance of machine learning models is so weaker than
binary method. However, the running time of those is always
more than others because of using large amount of epochs
and values related to some days before.
Overall, it is obvious that all the prediction models perform
well when they are trained with continuous values (up to
67%), but the models’ performance is remarkably improved
when they are trained with binary data (up to 83%). The
result behind this improvement is interpreted as follows: an
extra layer is employed in the second approach, and the duty
of the layer is comparing each current continuous value (at
time t) with previous value (at time t-1). So the future up or
down trend is identified and when binary data is given as the
input values to the predictors, we enter data with a
recognized trend based on each feature’s property. This
critical layer is able to convert non-stationary values in the
first approach to trend deterministic values in the second one,
and algorithms must find the correlation between input trends
and output movement as an easier prediction task.
Despite noticeable efforts to find valuable studies on the
same stock market, there is not any significant paper to
report, and this deficiency is one of the novelty of this
research. We believe that this paper can be a baseline to
compare for future studies.
V. Conclusions
The purpose of this study was the prediction task of stock
market movement by machine learning and deep learning
algorithms. Four stock market groups, namely diversified
financials, petroleum, non-metallic minerals and basic
metals, from Tehran stock exchange were chosen, and the
dataset was based on ten years of historical records with ten
technical features. Also, nine machine learning models
(Decision Tree, Random Forest, Adaboost, XGBoost, SVC,
Naïve Bayes, KNN, Logistic Regression and ANN) and two
deep learning methods (RNN and LSTM) were employed as
predictors. We supposed two approaches for input values to
models, continuous data and binary data, and we employed
three classification metrics for evaluations. Our experimental
works showed that there was a significant improvement in
the performance of models when they use binary data instead
of continuous one. Indeed, deep learning algorithms (RNN
and LSTM) were our superior models in both approaches.
REFERENCES
[1] Murphy, John J. Technical analysis of the financial
markets: A comprehensive guide to trading methods and
applications. Penguin, 1999.
[2] Turner, Toni. A Beginner's Guide To Day Trading
Online 2nd Edition. Simon and Schuster, 2007.
[3] Maqsood, Haider, et al. "A local and global event
sentiment based efficient stock exchange forecasting
using deep learning." International Journal of
Information Management 50 (2020): 432-451.
[4] Long, Wen, Zhichen Lu, and Lingxiao Cui. "Deep
learning-based feature engineering for stock price
movement prediction." Knowledge-Based Systems 164
(2019): 163-173.
[5] Duarte, Juan Benjamin Duarte, Leonardo Hernán Talero
Sarmiento, and Katherine Julieth Sierra Juárez.
"Evaluation of the effect of investor psychology on an
artificial stock market through its degree of
efficiency." Contaduría y Administración 62.4 (2017):
1361-1376.
[6] Lu, Ning. "A machine learning approach to automated
trading." Boston, MA: Boston College Computer Science
Senior Thesis (2016).
[7] Hassan, Md Rafiul, Baikunth Nath, and Michael Kirley.
"A fusion model of HMM, ANN and GA for stock

VOLUME XX, 2017 9
market forecasting." Expert systems with
Applications 33.1 (2007): 171-180.
[8] Huang, Wei, Yoshiteru Nakamori, and Shou-Yang
Wang. "Forecasting stock market movement direction
with support vector machine." Computers & operations
research 32.10 (2005): 2513-2522.gg
[9] Sun, Jie, and Hui Li. "Financial distress prediction using
support vector machines: Ensemble vs.
individual." Applied Soft Computing 12.8 (2012): 2254-
2265.
[10] Ou, Phichhang, and Hengshan Wang. "Prediction of
stock market index movement by ten data mining
techniques." Modern Applied Science 3.12 (2009): 28-
42.
[11] Liu, Fajiang, and Jun Wang. "Fluctuation prediction of
stock market index by Legendre neural network with
random time strength function." Neurocomputing 83
(2012): 12-21.
[12] Tsai, Chih-Fong, et al. "Predicting stock returns by
classifier ensembles." Applied Soft Computing 11.2
(2011): 2452-2459.
[13] AraúJo, Ricardo De A., and Tiago AE Ferreira. "A
morphological-rank-linear evolutionary method for
stock market prediction." Information Sciences 237
(2013): 3-17.
[14] Ballings, Michel, et al. "Evaluating multiple classifiers
for stock price direction prediction." Expert Systems
with Applications 42.20 (2015): 7046-7056.
[15] Basak, Suryoday, et al. "Predicting the direction of stock
market prices using tree-based classifiers." The North
American Journal of Economics and Finance 47 (2019):
552-567.
[16] Weng, Bin, et al. "Macroeconomic indicators alone can
predict the monthly closing price of major US indices:
Insights from artificial intelligence, time-series analysis
and hybrid models." Applied Soft Computing 71 (2018):
685-697.
[17] Long, Jiawei, et al. "An integrated framework of deep
learning and knowledge graph for prediction of stock
price trend: An application in Chinese stock exchange
market." Applied Soft Computing (2020): 106205.
[18] Rekha, G., et al. "Prediction of Stock Market Using
Neural Network Strategies." Journal of Computational
and Theoretical Nanoscience 16.5-6 (2019): 2333-2336.
[19] Pang, Xiongwen, et al. "An innovative neural network
approach for stock market prediction." The Journal of
Supercomputing (2018): 1-21.
[20] Kelotra, A. and P. Pandey, Stock Market Prediction
Using Optimized Deep-ConvLSTM Model. Big Data,
2020. 8(1): p. 5-24.
[21] Baek, Yujin, and Ha Young Kim. "ModAugNet: A new
forecasting framework for stock market index value with
an overfitting prevention LSTM module and a prediction
LSTM module." Expert Systems with Applications 113
(2018): 457-480.
[22] Chung, H. and K.-s. Shin, Genetic algorithm-optimized
long short-term memory network for stock market
prediction. Sustainability, 2018. 10(10): p. 3765.
[23] Kara, Yakup, Melek Acar Boyacioglu, and Ömer Kaan
Baykan. "Predicting direction of stock price index
movement using artificial neural networks and support
vector machines: The sample of the Istanbul Stock
Exchange." Expert systems with Applications 38.5
(2011): 5311-5319.
[24] Patel, Jigar, et al. "Predicting stock market index using
fusion of machine learning techniques." Expert Systems
with Applications 42.4 (2015): 2162-2172.
[25] Patel, Jigar, et al. "Predicting stock and stock price index
movement using trend deterministic data preparation
and machine learning techniques." Expert systems with
applications 42.1 (2015): 259-268
[26] Majhi, Ritanjali, et al. "Efficient prediction of stock
market indices using adaptive bacterial foraging
optimization (ABFO) and BFO based
techniques." Expert Systems with Applications 36.6
(2009): 10097-10104.
[27] Chen, Yingjun, and Yongtao Hao. "A feature weighted
support vector machine and K-nearest neighbor
algorithm for stock market indices prediction." Expert
Systems with Applications 80 (2017): 340-355.

VOLUME XX, 2017 9
Appendix section
TABLE 1
SELECTED TECHNICAL INDICATORS (N IS 10 HERE)
Simple n-day moving average (SMA) = 1 1
...
t t t n
C C C
n
− − +
+ + +
Weighted 14-day moving average (WMA) = 1 1
( 1) ...
( 1) ... 1
t t t n
n C n C C
n n
− − +
 + −  + +
+ − + +
Momentum (MOM) = 1
t t n
C C − +
−
Stochastic K% (STCK) =
_ 1 _ 1
_ 1
100
t t n t t n
t t t n
C LL
HH LL
− + − +
− +
−

−
Stochastic D% (STCD) =
1 1
...
100
t t t n
K K K
n
− − +
+ + +

Relative strength index (RSI) = 1
1
1
1
100
1
)
1 ( )
(
00 n
t i
i
n
t i
i
UP
DW
−
−
=
−
−
=
−
+ 

Signal(n)t (SIG) = ( ) 1
2
)
2
*(1
1
1
t t
M n
n
ACD Sig al n
n
−
 +
+
+
−
Larry William’s R% (LWR) =
_ 1
_ 1 _ 1
100
t t n t
t t n t t n
HH C
HH LL
− +
− + − +
−

−
Accumulation/Distribution oscillator (ADO) =
t t
t t
H C
H L
−
−
Commodity channel index (CCI) =
0.015
t t
t
M SM
D
−
While:
Ct is the closing price at time t
Lt and Ht is the low price and high price at time t respectively
LLt_t-n+1 and HHt_t-n+1 is the lowest low and highest high prices in the last n days respectively
UPt and DWt means upward price change and downward price change at time t respectively
EMA(K)t = ( ) 1
2 2
( )
1
1
1
t
t
EMA K C
k k
−
+
 
−
+
+
Moving average convergence divergence (MACDt) = EMA(12)t- EMA(26)t
Mt =
3
t t t
H L C
+ +
SMt =
1
0
n
t i
i
M
n
−
−
=

Dt =
1
0
n
t i t
i
M SM
n
−
−
=
−


VOLUME XX, 2017 9
TABLE 2
SUMMARY STATISTICS OF INDICATORS.
Feature Max Min Mean Standard Deviation
Diversified Financials
SMA 6969.46 227.5 1471.201 1196.926
WMA 3672.226 119.1419 772.5263 630.0753
MOM 970.8 -1017.8 21.77033 126.5205
STCK 99.93224 0.159245 53.38083 19.18339
STCD 96.9948 14.31843 53.34332 15.28929
RSI 68.96463 27.21497 50.18898 6.471652
SIG 310.5154 -58.4724 16.64652 51.62368
LWR 99.84076 0.06776 46.61917 19.18339
ADO 0.99986 0.000682 0.504808 0.238426
CCI 270.5349 -265.544 14.68813 101.8721
Basic Metals
SMA 322111.5 7976.93 69284.11 60220.95
WMA 169013.9 4179.439 36381.48 31677.51
MOM 39393.8 -20653.8 1030.265 4457.872
STCK 98.47765 1.028891 54.64576 16.41241
STCD 90.93235 12.94656 54.64294 13.25043
RSI 72.18141 27.34428 49.8294 6.113667
SIG 12417.1 -4019.14 803.5174 2155.701
LWR 98.97111 1.522349 45.36526 16.43646
ADO 0.999141 0.00097 0.498722 0.234644
CCI 264.6937 -242.589 23.4683 99.14922
Non-metallic Minerals
SMA 15393.62 134.15 1872.483 2410.316
WMA 8081.05 69.72762 985.1065 1272.247
MOM 1726.5 -2998.3 49.21097 264.0393
STCK 100.00 0.154268 54.71477 20.2825
STCD 96.7883 13.15626 54.68918 16.37712
RSI 70.89401 24.07408 49.67247 6.449379
SIG 848.558 -127.47 37.36441 123.9744
LWR 99.84573 -2.66648 45.28523 20.2825
ADO 0.998941 0.00036 0.501229 0.238008
CCI 296.651 -253.214 20.06145 101.9735
Petroleum
SMA 1349138 16056.48 243334.2 262509.8
WMA 707796.4 8580.536 127839.1 138101
MOM 227794 -136467 4352.208 26797.25
STCK 100.00 0.253489 53.78946 22.0595
STCD 95.93565 2.539517 53.83312 17.46646
RSI 75.05218 23.26627 50.02778 6.838486
SIG 71830.91 -33132 3411.408 11537.98
LWR 99.74651 -1.8345 46.23697 22.02162
ADO 0.999933 0.000288 0.498381 0.239229
CCI 286.7812 -284.298 14.79592 101.8417

ACCESS.2020.3015966.pdf

More Related Content

ACCESS.2020.3015966.pdf