Application of Buckley-Leverett Equation in Modeling the Radius of Invasion in a Reservoir Undergoing Microbial Enhanced Oil Recovery

International Journal of Engineering Research and Development
e-ISSN: 2278-067X, p-ISSN: 2278-800X, www.ijerd.com
Volume 11, Issue 09 (September 2015), PP.08-17
8
Application of Buckley-Leverett Equation in Modeling the Radius
of Invasion in a Reservoir Undergoing Microbial
Enhanced Oil Recovery
Nmegbu, C. G. J1
Wemedo, S. A2
, Obah, B .A3
and George, I. S4
1
Department of Petroleum Engineering, Rivers State University of Science and Technology,
Port Harcourt, Nigeria.
2
Department of Applied and Environmental Biology, Rivers State University of Science and Technology,
Port-Harcourt, Nigeria.
3
Department of Petroleum Engineering, Federal University of Technology, Owerri, Nigeria.
4
Department of Petroleum Engineering, Rivers State University of Science and Technology,
Port-Harcourt, Nigeria.
Abstract:- A thorough review of existing literature indicates that the Buckley-Leverett equation only analyzes
waterflood practices directly without any adjustments on real reservoir scenarios. By doing so, quite a number
of errors are introduced into these analyses. Also, for most waterflood scenarios, a radial investigation is more
appropriate than a simplified linear system. This study investigates the adoption of the Buckley-Leverett
equation to estimate the radius invasion of the displacing fluid during waterflooding. The model is also adopted
for a Microbial flood and a comparative analysis is conducted for both waterflooding and microbial flooding.
Results shown from the analysis doesn’t only records a success in determining the radial distance of the leading
edge of water during the flooding process, but also gives a clearer understanding of the applicability of
microbes to enhance oil production through in-situ production of bio-products like bio surfactans, biogenic
gases, bio acids etc.
Keywords:- Waterflooding, Buckley-Leveret, Radial invasion, Microbial flooding
I. INTRODUCTION
Waterflooding is the widely used secondary recovery or IOR option. It is an age-long practice of the oil
and gas industry that involves the use of injected water to increase production from oil reservoirs. The principal
reason for waterflooding an oil reservoir is to increase the oil-production rate and ultimately, the oil recovery [1].
The foremost attempt to improve sweep efficiency in waterflooding was made by Detling in 1944 [1], [2]. He
patented a number of additives, including water-soluble polymers to increase the viscosity of injected water and
the sweep efficiency of the flood. Some other additives in practice included surfactants, polymers, alkaline etc.
Waterflooding projects are usually faced with various challenges, specifically the effect of oil and water
viscosity on waterflood performance. This could be remedied by various techniques, one of which involves the
application of microbial flooding. Microbial flooding involves the injection of microorganisms that react with
reservoir fluids to assist in the production of residual oil [3]. A number of attempts to model MEOR have been
made, but it is still unclear if theoretical results reflect real field practices. Developing mathematical models for
MEOR is very challenging since physical, chemical and biological factors need to be considered [4], [5].
However, these models have not yet given any thorough description of the movement of the microbial injection
front.
When reservoir engineers analyze the waterflood performance, they resort to the conventional frontal
advance theory. In fluid dynamics, the Buckley–Leverett equation is a conservation equation used to model two-
phase flow in porous media The Buckley-Leverett displacement mechanism has been used to predict the
performance of waterflood. With Buckley-Leveret method, oil recovery from waterflood is calculated and the
required water injection volume to achieve that oil recovery is estimated. The equation can be interpreted as a
way of incorporating the microscopic effects due to capillary pressure in two-phase flow into D’arcy equation.
[6]. Leverett in his pioneering article presented the concept of fractional flow. Beginning with the Darcy’s law
for water and oil 1-D flow, he formulated the fractional flow equation [7] Again, in 1946, Buckley and Leverett
presented the frontal advance equation. Applying mass balance to a small element within the continuous porous
medium, they expressed the difference at which the displacing fluid enters this element and the rate at which it
leaves it in terms of the accumulation of the displacing fluid [8]. This led to a description of the saturation
profile of the displacing fluid as a function of time and distance from the injection point. The most remarkable

Application of Buckley-Leverett Equation in Modeling the Radius of Invasion in a Reservoir Undergoing
9
outcome of their displacement theory was the presence of a shock front. In 1952, a tangent construction method
was proposed by Welge to estimate the water saturation, water fraction at the water front and oil recovery factor.
Several other investigators studied the multilayer reservoir waterflood performance [9]. Reservoir engineers
suggest that Buckley-Leverett method assumed that fluid displacement occurs in a linear system. This could
work for some waterflood scenarios while for others it would not [10]. A thorough review of existing literature
indicates that petroleum engineers apply the Buckley-Leverett method to analyze waterflood projects directly
without any adjustments on the real reservoir and production situations. By doing so, a lot of errors are
introduced into the analysis. However, this study focuses on giving a radial investigation of the B-L equation
during waterflooding and also adopted for a microbial flooding project. As a performance monitoring method, it
is important to estimate the radial travel of injected water with microbial by-product, during microbial flooding.
II. METHODOLOGY
Oil recovery using microbes (MEOR) utilizes the effect of microbial solutions on a reservoir. The
MEOR processes very similar to the waterflood process, the difference being that the injection fluid is a mixture
of water and specially selected microbes. This mixture is such that the water is the continuous phase, while the
microbes are additives. The reservoir is usually conditioned by water pre-flush, and then the main slug, which is
a solution of microbes and nutrient is injected. As this solution pushes through the reservoir bio-products are
formed which includes biogas production for reservoir re-pressurization, biosurfactants are also produced to
reduce interfacial tension, bio acid for stimulation processes etc. A combination of all these processes helps
mobilize residual oil. The resulting oil and microbial product solution is then pumped out through production
wells.
A. Model development
The under listed assumptions serve as a basis for the development of the modified Buckley-Leverett
Equation for microbial flooding:
 One dimensional radial flow in a homogeneous, isotropic, isothermal, porous medium
 Reservoir is considered circular and fluids in the reservoir are incompressible, dispersion is negligible,
 Negligible gravitational force
 No fingering occurs
 Darcy’s law applies, hence flow is laminar
 The initial distribution of fluids is Uniform
 A continuous injection of constant composition fluid mixture (water plus microbes)
 No faults or folds within the reservoir.
B. The Radial invasion Equation
Just as the original Buckley-Leveret frontal advance model for 1-D, a mass balance equation is given for
the water and microbial by-product front in radial form as shown in figure 1.
For the unit reservoir rock system (i.e. at the position of the front), the mass balance equation then becomes;
(1)
Considering each part of (1) separately;
in (microbial by-product + water) = - density x velocity x cross-sectional area = - 𝜌w+mbp ∙ 𝑢r ∙ 𝐴
Therefore, (2)

10
Fig. 1: Circular reservoir showing the direction of flow during injection
out (microbial by-product + water) = - (3)
Assuming that there is neither source nor sink in the control volume (i.e. mass is neither a generated nor
consumed)
= 0 (4)
The rate of mass-accumulation in the control volume, taking it that the mass accumulation in the control volume
at any time is the product of pore volume (Vpore), the density of the fluid mix ( ) and saturation (Sw+mbp).
The rate of mass accumulation in the control volume is given by the change in mass from time (t+ t), divided
by the change in time, t.
Vpore = h S (in terms of Saturation) (5)
Mass accumulation =
(6)
Substituting (2), (3), (4) and (6) into (1), we have;
(7)
Simplifying (7) by opening up brackets;
(8)
Collecting like terms and simplifying;
(9)
Again, simplifying (9) further, we have;
(10)
Re-arranging (10) such that;
(11)
As the mixture of water and microbial product front approaches the boundary of the control volume, i.e.
as , (11) then becomes;
(12)
For total flow rate of the system;
= (13)
And
(14)
(15)
Substituting (15) into (12) and assuming the density of the water and microbial mix is constant with distance
and time; also assuming that total injection rate is constant with respect to distance travelled by the front, we
have;

11
(16)
Re-arranging;
(17)
In (17), expressing the cut of water and microbial by-product mix as a function of saturation ( ) {i.e.
( ), by applying chain rule;
(18)
This then implies that;
(19)
Integrating both sides of (19), we have an equation for the radial distance travelled by the front, from the
injector wellbore (i.e. the radius investigated) for any given time (t)
(20)
(21)
Simplifying equation, to give;
(22)
The correct solution for (22) is given by
(23)
Thus, (23) is the modification to the Buckley-Leveret equation to monitor radial displacement of the injection
front in a reservoir undergoing microbial flooding. Using the equation in its direct form would at best determine
the radial displacement of the chase fluid which is injected after the inoculation and subsequent soaking and/or
incubation period.
To determine the radial displacement of water plus microbes mix in the reservoir for the Microbial flooding
process, (23) can be expressed as;
(24)
In (23), the total injection rate, was expressed such that the effects of microbial concentration Cb on the
injection front is incorporated in the expression. The rationale behind this substitution stems from the fact that
the injected water acts as a vehicle for the microbes.
(23) and (24) have been deduced with (23) being the modification of the Buckley-Leveret (B-L) equation to
determine the radial displacement of the injection front. This expression when applied to a microbial flooding
case, would describe the movement of the chase fluid after the soaking/ incubation period, but is nevertheless
applicable to a general waterflooding scenario. On the other hand, (24) gives the radial distance of the
modification during a microbial flood.
C. Effects of Microbial growth rate on the invasion model
Microbial transport in porous media is governed by many complicated physical, chemical and biological
aspects such as sorption, interaction between microbes and nutrient, chemotaxis, growth and decay of the cells.
Among these, effect of growth rate of the cells of microorganisms is quite prominent.
In most MEOR literature, microbial growth is assumed to follow the classic Monod equation, which is given by;
(25)
Expressing the (25) in terms of changing substrate concentration with time, we have;
(26)
Where;
= substrate concentration (mg/l or lb/ft3
)
= maximum specific growth rate (day-1
)
B = Biomass concentration (mg/l or lb/ft3
)
Y = Yield Concentration (mg/L of biomass produced per mg/L of substrate degraded

12
= substrate concentration where the specific growth rate has half its maximum value.
The values of the parameters required for evaluating (26) can be obtained from experimental results.
Substituting (26) into (24) in order to replace , since concentration changes with time, gives;
(27)
Thus we then have;
(28)
D. Model Validation
1). Field Description: Field-X, is a sandstone formation with already existing waterflooding scheme. A
pilot test is being carried out on the field to evaluate MEOR success therein. The following data are for the pilot
injection well and general reservoir data for the field alongside data from experimental analysis of cores after
microbe injection for 100 days.
Table 1: Parameters for Model Analysis (Field and Experimental Data)
RESERVOIR DATA
Well bore radius (rw) 0.25ft
Porosity ( ) 20%
Formation thickness (h) 100ft
Dip angle ( ) 0o
Connate Water Saturation (Swc) 20%
Initial Water Saturation (Swi ) 20%
Residual Oil Saturation (Sor) 20%
Oil FVF (Bo) 1.25bbl/STB
Water FVF (Bw) 1.02bbl/STB
Oil viscosity 2.0cp
Water viscosity 1.0cp
Total injection rate 250 BWPD
EXPERIMENTAL DATA
( day-1
) 2
, (lb/ft3
) 5
, (lb/ft3
) 40
, (lb/ft3
) 6.243
Y, (yield coefficient) 0.53
Bbiomass concentration, B (lb/ft3
): 2.497
Table 2: Relative permeability, Saturation of water and microbes, and water and microbes cut
0.00 0.20 0.30 0.40 0.53 0.63 0.73 0.83 0.93 0.98 1.00
0.480 0.310 0.180 0.080 0.030 0.003 0.000 0.000 0.000 0.000 0.000
0.00 0.00 0.02 0.06 0.15 0.26 0.40 0.50 0.50 0.50 0.50
0.00 0.00 0.12 0.49 0.83 0.96 0.99 1.00 1.00 1.00 1.00
III. RESULTS AND DISCUSSION
Using the data retrieved from Field-X and microbial parameters presented above, certain parameters
required for the deduced invasion equation were calculated. Plots of relative permeability of oil and water (
and ) with increasing saturation is generated and critically observed to ensure that the selected reservoir
follows the same trend as Buckley and Leveretts’s. However, a similar trend is observed in Fig.2 below;

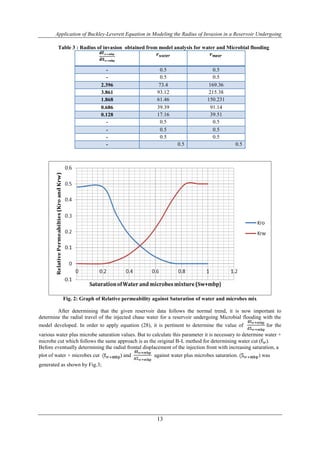
13
Table 3 : Radius of invasion obtained from model analysis for water and Microbial flooding
- 0.5 0.5
- 0.5 0.5
2.396 73.4 169.36
3.861 93.12 215.38
1.868 61.46 150.231
0.686 39.39 91.14
0.128 17.16 39.51
- 0.5 0.5
- 0.5 0.5
- 0.5 0.5
- 0.5 0.5
Fig. 2: Graph of Relative permeability against Saturation of water and microbes mix
After determining that the given reservoir data follows the normal trend, it is now important to
determine the radial travel of the injected chase water for a reservoir undergoing Microbial flooding with the
model developed. In order to apply equation (28), it is pertinent to determine the value of for the
various water plus microbe saturation values. But to calculate this parameter it is necessary to determine water +
microbe cut which follows the same approach is as the original B-L method for determining water cut ( ).
Before eventually determining the radial frontal displacement of the injection front with increasing saturation, a
plot of water + microbes cut ) and against water plus microbes saturation. ) was
generated as shown by Fig.3;

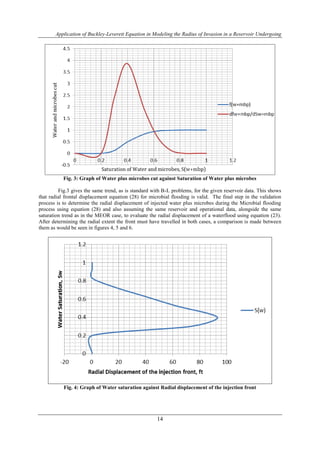
14
Fig. 3: Graph of Water plus microbes cut against Saturation of Water plus microbes
Fig.3 gives the same trend, as is standard with B-L problems, for the given reservoir data. This shows
that radial frontal displacement equation (28) for microbial flooding is valid. The final step in the validation
process is to determine the radial displacement of injected water plus microbes during the Microbial flooding
process using equation (28) and also assuming the same reservoir and operational data, alongside the same
saturation trend as in the MEOR case, to evaluate the radial displacement of a waterflood using equation (23).
After determining the radial extent the front must have travelled in both cases, a comparison is made between
them as would be seen in figures 4, 5 and 6.
Fig. 4: Graph of Water saturation against Radial displacement of the injection front

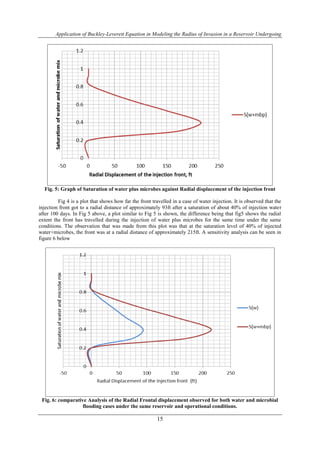
15
Fig. 5: Graph of Saturation of water plus microbes against Radial displacement of the injection front
Fig 4 is a plot that shows how far the front travelled in a case of water injection. It is observed that the
injection front got to a radial distance of approximately 93ft after a saturation of about 40% of injection water
after 100 days. In Fig 5 above, a plot similar to Fig 5 is shown, the difference being that fig5 shows the radial
extent the front has travelled during the injection of water plus microbes for the same time under the same
conditions. The observation that was made from this plot was that at the saturation level of 40% of injected
water+microbes, the front was at a radial distance of approximately 215ft. A sensitivity analysis can be seen in
figure 6 below
Fig. 6: comparative Analysis of the Radial Frontal displacement observed for both water and microbial
flooding cases under the same reservoir and operational conditions.

16
Fig. 7: Comparative analysis showing the water invaded zone and MEOR invaded zone
Ordinarily, it would be expected the injected water plus microbes should travel slower than the water
on the basis of density. But it should be noted that MEOR is a holistic approach to enhancing oil recovery and
by production of certain metabolites such as biomass, biosurfactants, biogenic gases, to mention a few, mobility
is affected positively and as such a faster and better sweep is achieved as shown in figure 7. In waterflooding,
the farther the leading edge, the efficient the sweep. The microbial flood recorded a greater radial sweep as
when compared to the convectional water flooding, implying an increased production rate at the wellbore.
IV. CONCLUSION
This study has successfully shown that a radial investigation can be made in a waterflooding process
using the B-L equation. The microbial application of the developed model also recorded a considerable success,
showing the radius of both microbial injection and water injection. Figure 6 gives a vivid description of the
comparative analysis for water flooding alone and microbes + water floods. As earlier discussed, the density of
the microbial flood makes it ideal to record a lower radius of investigation. However, the obtained results are
justifiable on the grounds that the microbial metabolites such as bio-surfactants, bio gases bio-acids produced
assisted in reducing interfacial tension between the formation and residual oil, reservoir pressurization as a
result of solution biogenic gases and formation stimulation for increased permeability respectively.
prediction of the radius of invasion of the injected fluid (ri) depends on a number of factors such as the injection
well radius (rw), porosity , reservoir thickness (h), fluid injection rate ( ), microbial concentration ( ),
injection time (t), injected fluid cut ( ) and saturation of water + microbial bio-products )
The investigation, however, does not take into account the complexity of a reservoir system; it is hence
recommended that further research be conducted for complex reservoir systems with existing faults and folds to
ascertain a radial front in such a condition.
ACKNOWLEDGMENT
The authors wish to appreciate Pepple Daniel Dasigha and Lotanna Ohazuruike Vitus for their contributions to
the fruitiness of this study.
REFERENCES
[1]. L. W Lake, 2014. PetroWiki. [Online] Available at: http://petrowiki.org/Waterflooding[Accessed 20
January 2015].
[2]. Carcoana, 1992. Applied Enhanced Oil Recovery. New Jersey: Prentice-Hall Incorporated.
[3]. R. E Terry, 2001. Enhanced Oil Recovery. In: Encyclopedia of Physical Science and Technology.
Brigham: Robert A. Meyers Ed., Academic Press, pp. 503-518.
[4]. Wikipedia, 2012. Wikipedia. [Online] Available at:
http://en.wikipedia.org/wiki/Microbial_enhanced_oil_recovery
[Accessed 26 February 2015].
[5]. M. Magot, (2005). Indigenous microbial communities in oil fields. In ‘‘Petroleum microbiology’’ (B.
Ollivier and M. Magot, Eds.), pp. 21–34. ASM, Washington, DC.
[6]. S. Buckley, S. & S. Leverett, 1942. Mechanism of fluid displacements in sands. Transactions of the
AIME, Issue 146, p. 107–116.

17
[7]. R. G Rustam, 2005. Modification of the Dykstra-Parsons Method to Incorporate Buckley-Leverett
Displacement Theory for Waterfloods. Texas: Texas A&M University.
[8]. Craft, B. & Hawkins, M., 1991. Applied Reservoir Engineering. 2nd ed. s.l.:Prentice-Hall,
Incorporated.
[9]. H. J. Welge, 1952. A simplified method for computing oil recovery by gas or water drive. Petrol Trans
AIME, Issue 195.
[10]. K. Ling, 2012. Fractional Flow in Radial Flow System—A Study for Peripheral Waterflood, Mexico
City: SPE Latin American and Caribbean Petroleum Engineering Conference.
[11]. R. Cosse, 1993. Basics of Reservoir Engineering. Paris: Editions Technip.
[12]. L. Dake, 1998. Fundamentals of Reservoir Engineering. 7th ed. Amsterdam, The Netherlands: Elsevier
Science B.V.
[13]. H. Dykstra, & R. Parsons, 1950. The Prediction of Oil Recovery by Waterflooding. Secondary
Recovery of Oil in the United States, p. 160–174.
[14]. J. F Fayers, 1981. Enhanced Oil Recovery. Amsterdam: Elsevier Scientific Publishing Company. Guha,
2005. Microbial Enhanced Oil - OIL's Experience, India: Oil India Limited.
[15]. R. Hamid,.2012. Microbial Enhanced Oil Recovery. In: L. Romero-Zerón, ed. Introduction to
Enhanced Oil Recovery (EOR) Processes and Bioremediation of Oil-Contaminated Sites. Croatia:
InTech, pp. 71-88.
[16]. Hiorth, 2007. Microbial Enhanced Oil Recovery - Mechanism. Calgary, Canada, Society of Petroleum
Engineers.
[17]. H. T. Kwak, A. A. Yousef, & S. H. Al-Saleh. 2014. New insights on the Role of Multivalent Ions in
Water-Carbonate Rock Interactions. The Saudi ARAMCO Journal Of Technology, III(3), pp. 25-37.
[18]. Magot, M., Caumette, P., Desperrier, J. M., Matheron, R., Dauga, C., Grimont, F., and Carreau, L.
(1992). Desulfovibrio longus sp. nov., a sulfate-reducing bacterium isolated from an oil-producing
well. Int. J. Syst. Bacteriol. 42, 398–403.
[19]. E. Premuzic, & A., Woodhead, 1992. Microbial Enhancement of Oil Recovery - Recent Advances. New
York, Elsevier Scientific Publishing Company.
[20]. C Wilson, 2002. Quantitive Methods in Reservoir Engineering. s.l.:Elsevier Incorporated

Application of Buckley-Leverett Equation in Modeling the Radius of Invasion in a Reservoir Undergoing Microbial Enhanced Oil Recovery

More Related Content

Application of Buckley-Leverett Equation in Modeling the Radius of Invasion in a Reservoir Undergoing Microbial Enhanced Oil Recovery