APS march meeting 2012
- 1. ARPES microscopy study on free standing bilayer graphene Po-Chun Yeh , Kevin Knox , Wencan Jin , Jerry Dadap , Philip Kim , Richard M. Osgood Columbia University Alexei Barinov, Dudin Pavel Elettra-Sincrotrone Trieste,Italy
- 2. Outline • Goal: To study electronic structure of free standing graphene • Brief review of our prior monolayer graphene studies • Bilayer – Theory and related studies – Sample preparation and apparatus – Data analysis – Comments
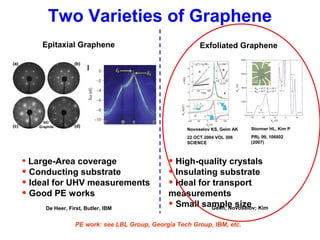
- 3. Two Varieties of Graphene Stormer HL, Kim P PRL 99, 106802 (2007) Novoselov KS, Geim AK 22 OCT 2004 VOL 306 SCIENCE Epitaxial Graphene Exfoliated Graphene • Large-Area coverage • Conducting substrate • Ideal for UHV measurements • Good PE works • High-quality crystals • Insulating substrate • Ideal for transport measurements • Small sample sizeDe Heer, First, Butler, IBM Geim, Novoselov; Kim PE work: see LBL Group, Georgia Tech Group, IBM, etc.
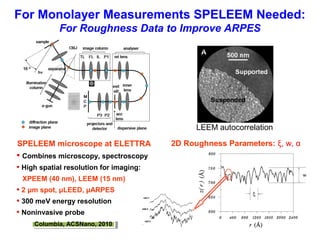
- 4. For Monolayer Measurements SPELEEM Needed: For Roughness Data to Improve ARPES SPELEEM microscope at ELETTRA • Combines microscopy, spectroscopy • High spatial resolution for imaging: XPEEM (40 nm), LEEM (15 nm) • 2 μm spot, μLEED, μARPES • 300 meV energy resolution • Noninvasive probe LEEM autocorrelation 2D Roughness Parameters: ξ, w, α α=0.5 α=0.3 α=0.7 α=0.5 α=0.3 α=0.7 α=0.5 α=0.3 α=0.7 Columbia, ACSNano, 2010Columbia, ACSNano, 2010
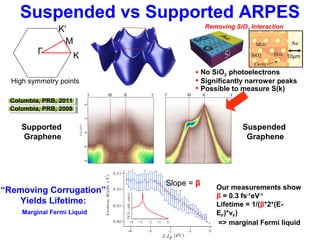
- 5. Suspended vs Supported ARPES Г M K K' Supported Graphene Suspended Graphene Columbia, PRB, 2008Columbia, PRB, 2008 Columbia, PRB, 2011Columbia, PRB, 2011 Our measurements show β = 0.3 fs-1 eV-1 Lifetime = 1/(β*2*(E- EF)*vF) => marginal Fermi liquid “Removing Corrugation” Yields Lifetime: Marginal Fermi Liquid High symmetry points • No SiO2 photoelectrons • Significantly narrower peaks • Possible to measure S(k) Removing SiO2 Interaction 10μm Slope = β
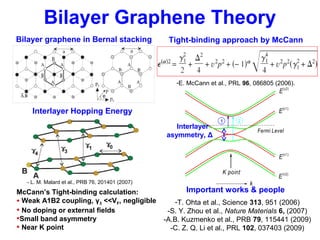
- 6. Bilayer Graphene Theory Bilayer graphene in Bernal stacking McCann’s Tight-binding calculation: • Weak A1B2 coupling, γ3 <<VF, negligible • No doping or external fields •Small band asymmetry • Near K point - L. M. Malard et al., PRB 76, 201401 (2007) -T. Ohta et al., Science 313, 951 (2006) -S. Y. Zhou et al., Nature Materials 6, (2007) -A.B. Kuzmenko et al., PRB 79, 115441 (2009) -C. Z. Q. Li et al., PRL 102, 037403 (2009) -E. McCann et al., PRL 96, 086805 (2006). Interlayer Hopping Energy Tight-binding approach by McCann Important works & people Interlayer asymmetry, Δ
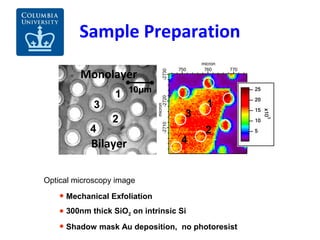
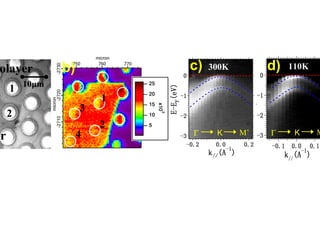
- 7. • 300nm thick SiO2 on intrinsic Si substrate • No substrate doping • Mechanical exfoliation • Free standing on 5μm wells • Shadow mask Au/Cr deposition, no photoresist • Overnight thermal radiation cleaning • Well defined layers, single domain Sample Preparation (Left) Optical microscopy image (Right)Spatially-resolved photoemission image: angle integrated mode at 15eV electron kinetic energy, by Spectromicroscopy. 1 2 3 4 Monolayer Bilayer 1 2 3 4 10μm
- 8. • Study the band structure and the Fermi surface topography • Temperature: 110K to 300K • Beam size: 0.6 - 1μm • Photon energy: 27eV • Momentum resolution: 2.7mÅ-1 • Energy resolution: 33meV SpectroMicroscopy at Elettra : Microscope + Monochromator -P. Dudin et al., J. Synchrotron Rad. (2010) 17 Cryostat Electron Analyzer Sample Counter Source Frequency selection Schwarzschild objective Elettra Sincrotrone, Trieste, Italy
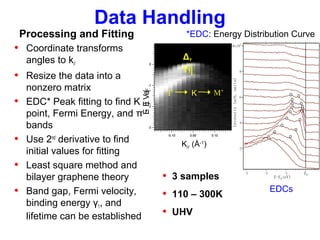
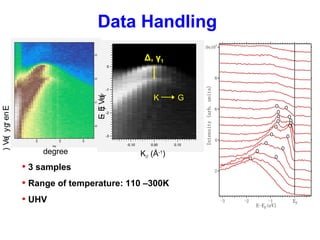
- 9. K// (Å-1 )E-EF(eV) Δ, γ1 Data Handling Processing and Fitting • Coordinate transforms angles to k// • Resize the data into a nonzero matrix • EDC* Peak fitting to find K point, Fermi Energy, and π bands • Use 2nd derivative to find initial values for fitting • Least square method and bilayer graphene theory • Band gap, Fermi velocity, binding energy γ1, and lifetime can be established • 3 samples • 110 – 300K • UHV EDCs *EDC: Energy Distribution Curve M’KΓ
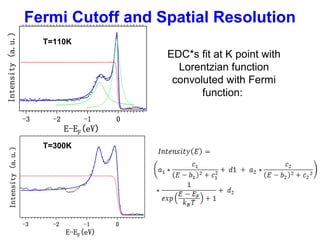
- 10. Fermi Cutoff and Spatial Resolution EDC*s fit at K point with Lorentzian function convoluted with Fermi function: T=110K T=300K
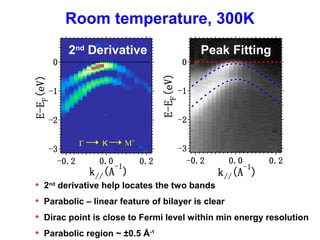
- 11. Room temperature, 300K 2nd Derivative2nd Derivative Peak Fitting • 2nd derivative help locates the two bands • Parabolic – linear feature of bilayer is clear • Dirac point is close to Fermi level within min energy resolution • Parabolic region ~ ±0.5 Å-1 M’KΓ
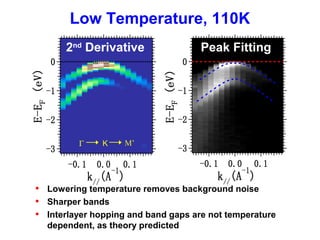
- 12. Low Temperature, 110K Peak Fitting2nd Derivative • Lowering temperature removes background noise • Sharper bands • Interlayer hopping and band gaps are not temperature dependent, as theory predicted M’KΓ
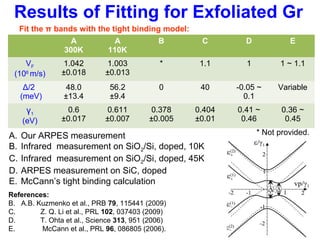
- 13. Results of Fitting for Exfoliated Gr Fit the π bands with the tight binding model: A 300K A 110K B C D E VF (106 m/s) 1.042 ±0.018 1.003 ±0.013 * 1.1 1 1 ~ 1.1 Δ/2 (meV) 48.0 ±13.4 56.2 ±9.4 0 40 -0.05 ~ 0.1 Variable γ1 (eV) 0.6 ±0.017 0.611 ±0.007 0.378 ±0.005 0.404 ±0.01 0.41 ~ 0.46 0.36 ~ 0.45 A. Our ARPES measurement B. Infrared measurement on SiO2/Si, doped, 10K C. Infrared measurement on SiO2/Si, doped, 45K D. ARPES measurement on SiC, doped E. McCann’s tight binding calculation References: B. A.B. Kuzmenko et al., PRB 79, 115441 (2009) C. Z. Q. Li et al., PRL 102, 037403 (2009) D. T. Ohta et al., Science 313, 951 (2006) E. McCann et al., PRL 96, 086805 (2006). * Not provided.
- 14. Summary and Direction Characteristics Fermi velocity, VF Interlayer asymmetry, Δ Interlayer coupling, γ1 – Strain ? – > 2ML – data looks too clean for this. – Additional measurements Zero-to-minimally-doped graphene measured • Chemical doping experiments needed • Surface corrugation and width broadening • Band asymmetry and renormalization
- 15. Thank you
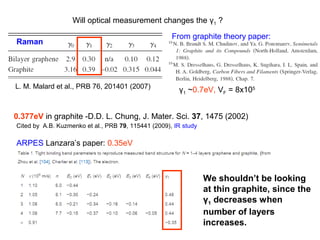
- 16. L. M. Malard et al., PRB 76, 201401 (2007) Raman From graphite theory paper: Will optical measurement changes the γ1 ? γ1 ~0.7eV, VF = 8x105 Cited by A.B. Kuzmenko et al., PRB 79, 115441 (2009), IR study 0.377eV in graphite -D.D. L. Chung, J. Mater. Sci. 37, 1475 (2002) ARPES Lanzara’s paper: 0.35eV We shouldn’t be looking at thin graphite, since the γ1 decreases when number of layers increases.
- 17. Results of Fitting for Exfoliated Gr Normal Temperature • Δ/2 = 48.0±13.4meV • γ1 = 0.6±0.017eV • VF = (1.042±0.018)x106 m/s Low Temperature • Δ/2 = 56.2±9.4meV • γ1 = 0.611±0.007eV • VF = (1.003±0.013)x106 m/s ARPES results, fit the π bands with McCann’s model: • Δ = 0 • Δ’ = 15±5meV • γ1 = 0.378±0.005eV • γ4 = 0.12eV • VF = Not provided IR, exfoliated, n-doped, 10K SiC, K doped • Δ = -0.1 – 0.2 meV • γ1 = 0.41 – 0.46 eV • VF = 1x106 m/s • Δ = variable • γ1 = 0.36 – 0.45eV • VF = (1 – 1.1)x106 m/s McCann’s theory IR, 45K, band asymmetry • Δ/2 < 40meV • Δ’ = 18±2meV • γ1 = 0.404±0.01, 0.450eV • γ4 = 0.04eV • VF = 1.1x106 m/s A.B. Kuzmenko et al., PRB 79, 115441 (2009) Z. Q. Li et al., PRL 102, 037403 (2009) E. McCann et al., PRL 96, 086805 (2006).T. Ohta et al., Science 313, 951 (2006)
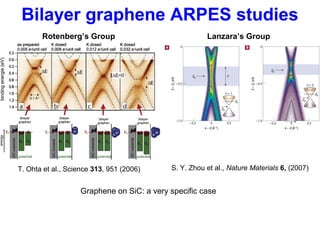
- 18. Bilayer graphene ARPES studies T. Ohta et al., Science 313, 951 (2006) S. Y. Zhou et al., Nature Materials 6, (2007) Graphene on SiC: a very specific case Rotenberg’s Group Lanzara’s Group
- 19. Linewidth broadening • Quasiparticle's lifetime is inversely proportional to the linewidth(FWHM) in Breit- Wigner line shape. • Linewidth are affected by two major effects: Corrugation broadening and intrinsic broadening. • In bilayer graphene, we should expect a mild corrugation broadening.
- 20. Corrugation Broadening • Surface roughness of the graphene sample provides ripples with phase shift as a wave in a continuum. • Electron scattering • Corrugation parameters: ξ, ω, and α; acquire from LEEM and LEED measurement. • Calculation: A~ Lorentzian, obtainable by fitting MDCs.
- 21. Intrinsic Broadening • Changes with different photon energies. • Since graphene is a 2D crystal, the valence band initial states are highly localized along z direction – band structure is kz independent, thus it will not change with different photon energy. • We have only one photon energy 27eV.
- 22. Sample Preparation • Mechanical Exfoliation • 300nm thick SiO2 on intrinsic Si • Shadow mask Au deposition, no photoresist Optical microscopy image 1 2 3 4 Monolayer Bilayer 1 2 3 4 10μm
- 23. Energy(eV) degree GK K// (Å-1 ) E-EF(eV) • 3 samples • Range of temperature: 110 –300K • UHV Data Handling Δ, γ1
- 24. 1 2 3 4 olayer er 1 2 10μm 300K 110Kb) c) d) M’KΓ MKΓ
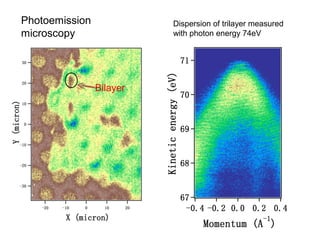
- 25. Photoemission microscopy Bilayer Dispersion of trilayer measured with photon energy 74eV
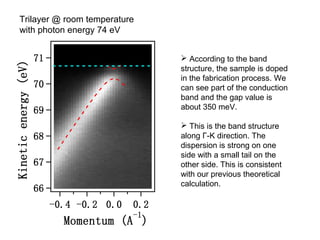
- 26. Trilayer @ room temperature with photon energy 74 eV According to the band structure, the sample is doped in the fabrication process. We can see part of the conduction band and the gap value is about 350 meV. This is the band structure along Γ-K direction. The dispersion is strong on one side with a small tail on the other side. This is consistent with our previous theoretical calculation.
Editor's Notes
- Emphasize free standing/ suspended.
- To provide context, I am going to give a brief review of …
- Don’t say “recent” work.
- Ref: low energy electron microscope (LEEM) and energy filtered x-ray photoemission electron microscope (XPEEM.)
- Imaginary part of internal energy v.s. binding energy - &gt; slope = β
- Backup knowledge: Bernal stacking, tight-binding theory, assumptions… Remake the band structure to emphasize the zero gap case
- Don’t over emphasize on the energy resolution. Say it has ten times higher resolution than SPELEEM, and it can let us look at the band structure around the K point.
- Stress on data handling requires a series of processing Points: 2nd derivative… and Least square value
- Chirp by Fermi Function.
- 1. Symmetry mismatch in sample and the incoming light; the optical matrix and the sample matrix are different.
- There is a small band gap in our data, but it is within our error bar γ1 is sample dependent. (From Kuzmenko’s paper.)
- Explanations: 1. 2.
- The bang gap falls into our minimum energy resolution, so we are not sure if there’s actually a very small gap or no gap. (Intrinsic band gap?) How all these compare to SiC data? IR data? γ1 is sample dependent. (From Kuzmenko’s paper.)
- Breaks A-B symmetry, creating a band gap Effect of layer inequivalence Suspension eliminate most of the unwanted scattering mechanisms enhancing the effect of electron-electron interaction, which makes bands anisotropic, or directionally dependent.