Basic statistical Measues.ppt

MBBS.USMLE, DPH, Dip-Card, M.Phil, FCPS
Professor Community Medicine/Epidemiolgy
Ex- Professor Community Medicine
UmulQurrah University Makka Saudi Arabia

Monday, May 15, 2023 Prof Muhammad Tauseef Jawaid 2
What is statistics
Science of assembling, classifying, tabulating and
analyzing the data in order to make generalization and
decisions
1. Descriptive Statistics
2. Inferential Statistics

Descriptive Statistics
Methods of organizing and summarizing
Data/information
1. Construction of tables, graphs, Charts
2. Calculation of descriptive measures
a) Averages
b) Dispersions
c) Other descriptive landmarks, range, minimum,
maximum etc.

Inferential Statistics
Methods of drawing conclusion about the
population from the data obtained from a
sample of that population
Describing the sample data
Drawing conclusion about the population

Population
Inference
Descriptive Statistics
Inferential
Statistics
Sample

Brain storming
What is normal standard height for
Pakistani adult man and woman?
What is normal Cholesterol or Hb for
Pakistani adult male and female?

Why we study statistics for Medicine?
To develop normal healthy population
parameters
Height, weight, mid-arm circumference etc.
Hb, Cholesterol, LDL, HDL etc.
Behaviors, vital parameters
To describe the observed population
parameters
To compare the observed with the normal
standards

DATA
Latin : Datum
Something assumed as facts and made the
basis of reasoning or calculation.
1. Qualitative or Categorical
Sex, Colour, Race
2. Quantitative or Numerical
Age, Height, Parity

Variables
Qualitative Quantitative
Categorical/
Ordinal
Nominal Continuous Discreet
Quantitative and
qualitative
Classifying variables

Categorical Data
 Nominal: categories of data cannot be ordered one
above the other.
Sex: Male, Female
Marital Status: Single, Married, Divorced,
 Ordinal: Categories of the data can be ordered one above
the other or voice versa.
Level of knowledge: Good, Average, Poor
Opinion: Fully Agree, Agree, Disagree

Variable
An item of data that can be observed or
measured.
Quantitative Variable
A variable that has a numerical value e.g.
Age, No. of Children
Qualitative Variable
A variable that is not characterized by a
numerical value.
e.g. Sex, Category of Diseases

Quantitative Variables
Discrete Variable
A quantitative variable, whose possible values are
in whole numbers.
Example: No of visits to a GP.
No. of Children
Continuous Variable
A quantitative variable that has an un interrupted
range of values
Example: Blood Pressure, Weight

Types of Variables
• Independent Variable
A variable, whose effect is being measured. (Cause)
• Dependent Variable
The variable, on whom the effect is being observed.
(Effect)
• Confounding Variable
A variable, which affects both independent as well as
dependent variable (Cause as well as Effect)

Statistical Summaries/
Descriptive statistics
Qualitative variables
•Frequencies
•Simple frequency
•Relative frequency
•Cumulative frequency
•Percentages
•Proportions
•Ratios
Quantitative Variables
•Central values
•Mean
•Median
•Mode
•50th percentile
•Dispersions
•Range
•Mean deviation
•Standard deviation
•Variance
•Percentiles

Inferential Statistics
Analytical statistics
Associations
Correlations
Confidence Intervals Test of significance

Qualitative data descriptive
statistics
Inherently categorical and nominal variables
are described e.g. sex, race, educational
states,
Derived/converted categorical
Simple frequency
Relative frequency
Percentages
Proportions
Ratio

Grouping and frequency distribution
Age of 15 students is given as
21, 32, 29, 22, 21
25, 27, 23, 22, 25
26, 25, 30, 19, 25
Is it meaningful to describe as such?
How will you organize groups ?

Developing Classes or Groups
Cholesterol levels of 20 adult men from a village
are as under at village X
210, 295, 290, 150, 221
225, 160, 190, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Is it meaningful to describe as such?
How will you organize groups ?

Guidelines for Class Intervals
The class intervals must be equal
The class intervals must be logical
The starting interval must contain minimum value
The last interval must contain maximum value
Each given value can only be included in one class
Class interval must not be too small or too large

Logics for class intervals
What may be the logic of class interval for
age in Children?
What may the logics of class interval for
age in married women?
What may be logic of class interval for
weight of children?
What may be the logic of class interval for
Blood pressure and Cholesterol?

Tally Method of data sorting
Cholesterol levels of 20 adult
men are as under at
village Bugga Shekhan
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Class Intervals Freq.
150 to 174 /
175 to 199 /
200 to 224 //
225 to 249
250 to 274
275 to 300 /

Tally Method of data sorting
men are as under at
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Class Intervals Frequencies
150 to 174 /// 3
175 to 199 /// 3
200 to 224 //// // 7
225 to 249 /// 3
250 to 274 // 2
275 to 300 // 2

Frequency distribution of cholesterol
levels
men are as under at
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
150 to 199 //// / 6
200 to 249 //// //// 10
250 to 299 //// 4
Total 20

Term used in grouping of data
Classes:
(Categories for grouping)
Upper class limit: (Smallest value
in a class)
Lower class limit:
(largest value in the class)
Class Mark:
(Midpoint of a class)
Class Width or class interval:
(Difference between lower class
limit of the given class and lower
class limit of next higher class)
150 to 199 6
200 to 249 10
250 to 299 4
Total 20

Various frequency distributions
Frequency: Number of pieces of data in a
given class
Frequency distribution: Listing class and
their frequencies
Relative Frequency: Ratio of frequency of
a given class to total number of data
observed
Frequency percentage: Relative frequency
multiply by 100 (f/N x 100 = Percentage)

Simple frequency distribution
(Large class intervals)
150 to 199 6
200 to 249 10
250 to 299 4
Total 20

Cumulative frequency distribution
Class Interval Frequency
(f)
Cumulative
frequency
150-199 6 6
200-249 10 16
250-299 4 20.00

Relative frequency distribution
(f)
Relative
Frequency
150-199 6 0.30
200-249 10 0.50
250-299 4 0.20
Total (N) 20 1.00
Formula for Relative frequency = f/N
Relative frequency is the probability

Percentage distribution
(f)
Percentage
150-199 6 30.00
200-249 10 50.00
250-299 4 20.00
Total (N) 20 100.00
Formula for Percentage = f/N x 100

Frequency distribution chart
men are as under at
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Frequency distribution of Cholestrol
Levels in adult males at Bugga Shekhan
0
2
4
6
8
10
150-199 200-249 250-299
Cholestrol levels
Number
of
persons

Percentage distribution Chart
men are as under at
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Percentage distribution of
cholestrol levels
0
20
40
60
80
100
150-199 200-249 250-299
Cholestrol levels
Percentage

Relative frequency distribution
men are as under at
210, 295, 190, 150, 221
225, 160, 290, 202, 225
180, 175, 230, 219, 250
170, 215, 270, 200, 220
Relative Frequency distribution of
Cholestrol levels
0
0.1
0.2
0.3
0.4
0.5
150-199 200-249 250-299
Cholestrol level
Relative
frequency

Data Presentation
Tabulation Graphical Presentation
Simple Tables Complex Tables Crass tables 2x2 Tables Bar Charts
Histogram
Pie Charts
Frequency Polygons
Pictogram

Relative frequency and probability
The relative frequency of a given class is
the probability of that class
Relative frequencies of specified classes
is the probability of those classes

Probability distribution

Statistical Land marks for
describing data

Developing statistical land-mark for data
expression
Central mark
upper
Lower
Quarter
Quarter

Comparing the observed value with
the land-marks
Observed value
Observed value
Observed value

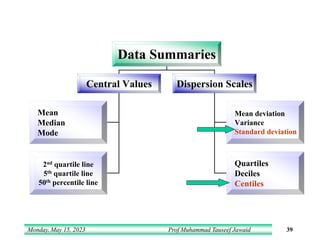
Data Summaries
Central Values Dispersion Scales
Mean
Median
Mode
2nd quartile line
5th quartile line
50th percentile line
Mean deviation
Variance
Standard deviation
Quartiles
Deciles
Centiles

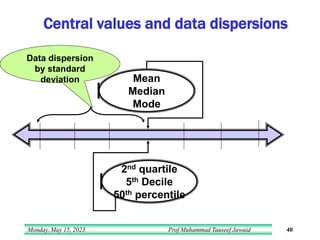
Central values and data dispersions
Mean
Median
Mode
2nd quartile
5th Decile
50th percentile
Data dispersion
by standard
deviation

Mean
Mean is mathematically calculated central
value of data
Mean =
Sum of the data values
Number of pieces of data

Notation of Mean
X1 + x2 + x3 …………..xi =  x
If n is the number of observation then
 x
X=
n
Mean
Number of observation
Sum of data

Calculation of mean
The IQ values of 8 Children is given as:
70 60 120 110
100 80 130 90
 x = 760 n = 8
760÷8 = 95
Mean IQ = 95

Scope and limitation of mean
Mean is central value of data which can be further
subjected to statistical evaluations in inferential
statistic
It is calculated by using values of all data sets
It is very sensitive to unusual extreme values
It is difficult to calculate

Median
1. Arrange the data set in increasing order
2. If number of pieces of data are “odd”, then
median is the data value exactly in the middle of
order list
3. If the number of pieces of data are “even”, then
median is the mean of the middle two data
value

Formula of Median
n + 1
2
Median = th value in case of odd data
number
n + 1
2
Median = Mean of the two central data
values in case of even number

Calculation of Median odd data set
Diastolic Blood pressure of 9 patiens
100,120,90,110,110,130,140,200,80
Arrange the data in ascending or
increasing order
80,90,100,110,110,120,130,140,200
n= 9
9+1/2 = 5 th value is the median

Calculation of Median by even data
set
Diastolic Blood pressure of 9 patients
100,120,90,110,110,130,140,200,80,240
Arrange the data in ascending or
increasing order
80,90,100,110,110,120,130,140,200,240
n= 10 10+1/2 = 5.5 than mean median
lies between 5th and 6th values e.g
110+120/2= 115 is the median

Scope and limitation of median
It is also very useful central value of data
It can be used for further statistical
analysis but it is less significant than mean
Its value does not vary with unusual
extreme values in the data
It is an important land mark for dispersion
of data
It can be calculated without treating all the
values for mathematical calculations

Mode
The most frequently occurring value in the data is defined as
mode
Consider the following data set of Hb levels
10.5, 11.0, 12.0, 11.5, 11.5, 9.5, 11.5, 12.0, 11.5, 10.5, 9.5,
11.5, 11.5, 10.5. 9
Arrange the data in to increasing order
9, 9.5, 9.5, 10.5, 10.5, 10.5, 11.0, 11.5, 11.5, 11.5, 11.5,
11.5, 11.5, 12.0, 12.0,
Therefore 11.5 will be the Mode in this data

Model Frequency
How many data set fall in model
value?
6 data set fall in model value
Total data pieces 15
9, 9.5, 9.5, 10.5,
10.5, 10.5, 11.0,
11.5, 11.5, 11.5,
11.5, 11.5, 11.5,
12.0, 12.0,
Model frequency =
No. of data pieces in mode
Total No. of observations
X 100

Scope and limitation of mode
It is very easy to estimate without much
calculations
It can not be subjected to further statistical
evaluation for inferential statistics
It is not modified by unusual extreme value in the
data
It is useful to describe the central tendency for
qualitative data (e.g. opinion of the people)

Summary
Measure of
Central
tendency
Definitions Expressions
Mean Sum of the data
No. of pieces of data
Median Middle value in ordered
list
Mode Most frequently
occurring value
Model frequency%
 x
X= n
n + 1
2

Data Dispersion
The pattern how the data is distributed
between minimum to maximum values of
measurement scales
The Pivotal land mark of data dispersions are
Central values most commonly used is mean
and least commonly used is mode

Types of data dispersions
Range
Deviation from the mean
Standard deviation
Quartile distribution
Deciles distribution
Percentile distribution

Range
Range is the difference between
minimum and maximum value in a data
set
Range = Max - Min
Range is quite easy to compute however in using the
rang great deal of information is ignored
It takes in to consideration only two value in a data
and rest of value are disregarded

Deviation from the Mean
Deviation from the mean gives the estimation
how much a given value far or nearer to the
mean of a data set
Consider a simple data set of heights of a
team given in inches
72 73 76 76 78

Calculation of deviation from the mean
Steps in calculation of mean
deviation
Calculate the mean of the
data by formula
375/5=75
Then calculate deviation
from the mean
 x
X=
n
Ht
x
Mean Ht x¯ Dev.
x- x¯
72 75 - 3
73 75 - 2
76 75 1
76 75 1
78 75 3
Mean deviation =
 | x- x¯|
n

Mean deviation
What will be total mean deviation
from given data set if it is
calculated by given formula
Is it equal to zero
Therefore mean deviation is not
significant measure of data
dispersion
Ht
X
Mean Ht
x¯
Dev.
x- x¯
72 75 - 3
73 75 - 2
76 75 1
76 75 1
78 75 3
 | x- x¯|
n

Calculation of Standard Deviation
Calculate the mean
Calculate deviation of each
observation
Take the squares of each
difference
Add all the squared
deviations
Divide all the sum of the
squared variation by n the
No. of observations the out
come is known as Variance
= 6 inche2
Ht
X
Mean Ht
x¯
Dev.
x- x¯
(x- x¯)2
72 75 - 3 9
73 75 - 2 4
76 75 1 1
76 75 1 1
78 75 3 9
24
variance =
 ( x- x¯)2
n-1

Calculation of Standard Deviation
Calculate the mean
Calculate deviation of each
observation
Take the squares of each
difference
Add all the squared deviations
Divide all the sum of the squared
variation by n the No. of
observations
Take the square root of the all
above steps it will give the
standard deviation
Ht
X
Mean Ht
x¯
Dev.
x- x¯
(x- x¯)2
72 75 - 3 9
73 75 - 2 6
76 75 1 1
76 75 1 1
78 75 3 9
24
Standard Deviation =
 ( x- x¯)2
n-1
= ±2.4

Significance of Standard Deviation
SD is measuring the variation in the individual values
of the data
Greater variant in the individual values grater will be
SD
SD has inverse relation with the sample size greater
the sample size less will be the SD
The central land mark of the SD is mean
SD is in ± signs mean it indicates dispersion of given
observation on either side of mean
In normal distributions we can estimate the frequency
of given observation in the population

Significance of Standard deviation
Standard deviation is the yard-stick that measure the
distance of a given value x from the Mean x
75
72 77
73 76 78
74
x
71 79
S. D = ±2.4 Inches
2.4 in
+1sd
2.4 in
-1sd
Where minus 2 S.D will fall?
At what S.D 79 and 71 are falling?

Landmarks of quartile
distribution?
Central measure is the median of the data
First Quartile line:
First quartile is median of data lying at or below the median of
the entire data
Second quartile line:
Median of the entire data
Third quartile line:
Third quartile is the median of the data lying at or
above the entire data

Quartiles of the data
First Quartile: The data lying at or below
the first line
Second quartile: The data lying between
first and second quartile lines
Third quartile: The data lying between
Second and third quartile line
Fourth quartile: The data lying above the
third quartile line

Finding the quartiles
25 41 27 32 43
66 35 31 15 5
34 26 32 38 16
30 38 30 20 21
Consider the following data set of weekly time
consumed for Television viewing by the 20 people
Arrange the data set in increasing order
5 15 16 20 21 25 26 27 30 30 31 32 32 34 35 38 38 41 43 66

Locating quartile land marks
n + 1
2
Median = =30 + 31 = 30.5
5 15 16 20 21 25 26 27 30 30 31 32 32 34 35 38 38 41 43 66
Q3 = 35 + 38 / 2 = 36.5
Q1 = 21 + 25 / 2 = 23.0
Q2 = 30 + 31 / 2 = 30.5
First Quartile line:
Second quartile line:
Third quartile line:

Quartile distribution
5 15 16 20 21 25 26 27 30 30 31 32 32 34 35 38 38 41 43 66
23.0 30..5 36.5
Q2 Q3
Q1
Quartile: 1 Quartile: 2 Quartile: 3 Quartile: 4

Deciles distribution
If we apply the same way of distribution as in
quartile and divide the data in 10 parts. The
median of the data will be 5th decile line and
D1, D2, D3, D4 will fall below the median. The
D6, D7, D8 and D9 will fall above the median.
D5
D4
D3
D2
D1
D6 D7 D8 D9

Percentile distribution
If we apply the same way of distribution as in
quartile and divide the data in 100 parts. The
median of the data will be 50th percentile and
P1, P10, P20, P40th will fall below the median.
The P60, P70, P90 and P100th will fall above
the median.
P50
P40
P30
P20
P10
P60 P70 P80 P90
P1 P100

Types of data dispersion/distribution
Normal distribution of data
Symmetrical distribution of data
Skewed distribution of data
Positively skewed
Negatively skewed
‘J’ distribution
Reverse ‘J’ distribution

Relative
frequency
/Probability
Measurement scale
Continuous probability Normal distribution

The Standard Normal distribution follows a normal
distribution and has mean 0 and standard deviation 1

0
3
6
9
12
15
Birth(0) 1 2 3 4 5 6 7 8 9 10 11 12
+2SD
+1SD
Mean
-1SD
-2DS
Developing Reference line for growth monitoring
chart using mean and SD landmarks
Increasing age of the birth cohort of normal children
Weight
in
Kg

0
3
6
9
12
15
Birth(0) 1 2 3 4 5 6 7 8 9 10 11 12
+2SD
+1SD
Mean
-1SD
-2DS
chart using mean and SD landmarks
Weight
in
Kg

0
3
6
9
12
15
Birth(0) 1 2 3 4 5 6 7 8 9 10 11 12
95th percentile
75th percentile
50th percentile
25th percentile
5th percentile
chart using median and percentile landmarks
Weight
in
Kg

0
3
6
9
12
15
Birth(0) 1 2 3 4 5 6 7 8 9 10 11 12
95th centile
25th centile
50th centile
25th centile
5th centile
chart using Median and Percentile landmarks
Weight
in
Kg

Boys Length and weight for age
(Birth to 36 Months)
Based on percentile distribution

Girls Length and weight for age
(Birth to 36 Months)
Based on percentile distribution

Properties of Normal distribution
Curve is bilaterally symmetrically
Mean, median and mode lies in the center of the
scale on x axis
The probability is shown by the area under curve
and total area is taken as one
The standard normal distribution curve extend
indefinitely in both direction
Probability/relative frequency varies from
minimum to maximum 0.5 in the center to
minimum on both side

Normal distribution Curve
When the data is plotted by relative frequency
and measurement scale it will produce a smooth
bell shaped curve that is known as Normal
distribution curve
If the dispersion of data is described in terms of
standard deviation from the mean the
probabilities are nearly fixed on given SD from
the mean
The dispersion is shown on X axis and relative
frequency or probability is shown on y axis

Properties of Normal distribution curve
Most of the area lies between -3 SD to +3 SD
The probabilities of key land mark are shown as
under
Z (SD) Area under curve
between –z and +z
Percentage of total
area
1 0.6826 68.26
2 0.9544 95.44
3 0.9974 99.74
1.96 0.9500 95.00

Properties of Normal distribution curve
Most of the area lies between -3 SD to +3 SD
The probabilities of key land mark are shown as
under
Z (SD) Area under curve
between –z and +z
Percentage of
total area
Probability
of error
1 0.6826 68.26
2 0.9544 95.44
3 0.9974 99.74
1.96 0.9500 95.00

Probability in normal distribution
Probability

Significance of normal distribution
curve
We can find the standard deviation of the
data
We can predict the probability of variable
at given dispersion points if we know the
standard deviation
We can predict the deviation from the
mean if we know the probability of the
variable
We use the normal distribution for
inferential statistics

Z Score
X- X
Z=
SD
The distance of a given value from the
mean in terms of standard deviation

What is z Score ?
Standard deviation is the yard-stick that measure the
distance of a given value x from the Mean x
75
72 77
73 76 78
74
x
71 79
S. D = ±2.4 Inches
2.4 in
+1sd
2.4 in
-1sd
Where minus 2 S.D will fall?
At what S.D 79 and 71 are falling?

Significance of Z Score
If we know the z score of an observed value we
can predict the probability of that value
We can estimate the probability between two
given z values by estimating the area under
normal distribution curve

Assignment
The mean age your workshop batch is 35
years and the Standard deviation is 5
years
Find your own z score (How many SD you
are away from the mean)?
If z score of student is -1.5 what is his
age?
How much percentage of class can fall
between -2 to +2 SD z scores?

Change in probability with z scores

Reference values of normality in Percentile
Distribution
50th percentile is the central value
corresponding to mean or median
Data within the 5th and 95th Percentile is taken
as normal
Quartile and Docile distribution are not used
to describe the reference of normality and
probability of error

Standard Errors (SE)
If we take sample mean; How far or nearer
it is, to actual population mean?
determined by SE
If we take sample proportion; How far or
nearer to population proportion?
Lesser the SE more precise you are

Two factors determining the SE
Standard Error is directly associated with
population variation or dispersion measured in
terms of standard deviation, greater the standard
deviation greater will be the standard error
Standard Error is inversely associated with sample
size greater the sample size less will be the
standard error

Steps for calculation of SE of the
mean
1. Take the sample from a reference population
2. Calculate the mean and Standard deviation
3. Calculate the standard Error by following
formula:
s.e =
n
s

Steps for calculation of Standard Error
of Proportion
Take a suitable sample from a reference
population
Calculate the proportion of interest
Calculate the SE of proportion by following
formula
P (1-P)
n
Standard Error of =
Proportion
P is the proportion and the multiplying factor is 1-p
and n is the sample size

Standard Error of Proportion
The frequency distribution of the samples
proportions would follow the SND curve
The mean of the of the samples proportions
would be equal to population p^
The standard deviation of these samples
proportions would be termed as Standard
Error of the Proportion

Standard Error of difference between
two means
Take the two samples of under comparison
Calculate the means and standard deviations
Calculate the Standard Error of difference
between two means by following formula:
s1
2+ s2
2
n1+n2
Standard Error of
difference of means =

Some terminology
P value
Accepted probability of error in decisions
Internationally accepted equal to 5% or 0.05 in
fraction
It can be stated or accepted below and above
0.05 depending upon study sample
It is also known as α error, type 1 error or
significance level
On two tail of normal curve it is /2 = 0.025 on
both side

Some important terms
Confidence level
It is equal to 1- (0.95 or 95%)
It is the probability of making correct decisions
(rejection the null hypothesis when it is false)
 Error or type II error
Probability of not rejecting null hypothesis when
it is in fact false

Confidence and  Error

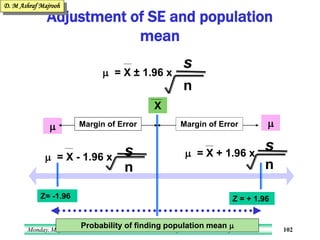
Adjustment of SE and population
mean
n
s
 = X ± 1.96 x
 
Margin of Error Margin of Error
Z = + 1.96
Z= -1.96
n
s
 = X + 1.96 x
n
s
 = X - 1.96 x
X
Probability of finding population mean 

Adjustment of SE and population
mean
Z = + 1.96
Z= -1.96
n
s
 = X ± 1.96 x
n
s
 = X + 1.96 x
n
s
 = X - 1.96 x
X
 
Margin of Error Margin of Error
Probability of finding population mean 
D. M Ashraf Majrooh

Standard Errors
Sample based
estimations
Errors Statistical test
Mean SE of the mean One sample t test
Proportion SE of proportion 95% Confidence
limits
Difference between
two means
SE of the difference
between two means
t test for
independent
samples
Difference between
two proportion
SE of the difference
between two
proportions
Chi-square and
comparison of two
proportions

Uses of Standard Errors
To predict the population mean from
sample mean (95% Confidence limits for
means)
To predict the population proportion from
sample proportion (95% Confidence limits for
means)
To find, whether the difference between
two mean is significant (at 0.05 probability of
error)
To find whether the difference between
two proportion is significant (at 0.05
probability of error)

20 40 60 80 100 120 140 160
Fasting Blood Sugar levels among normal and diabetic patients
Hypoglycemic Normoglycemic Hyperglycemic
How the statistics state the
significance difference

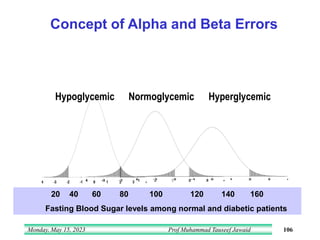
20 40 60 80 100 120 140 160
Fasting Blood Sugar levels among normal and diabetic patients
Hypoglycemic Normoglycemic Hyperglycemic
Concept of Alpha and Beta Errors

Standard Normal distribution curve

0
3
6
9
12
15
Birth(0) 1 2 3 4 5 6 7 8 9 10 11 12
-2SD
-1SD
Mean
+1SD
+2SD
chart using mean and SD as landmarks

Basic statistical Measues.ppt

More Related Content

Basic statistical Measues.ppt