Business mathematics presentation
- 2. SPECIAL THANKS TO Kazi Md. Nasir Uddin Assistant Professor Department of AIS Faculty Of Business Studies Jagannath University
- 3. GROUP MEMBERS Sl. Name ID 01. Sahnaj Akter M18150201701 02. Md. Akashur Rahman M18150201702 03. Madhobi Akter M18150201703 04. Meghna Philomena Rozario M18150201704 05. Sourov Shaha Suvo M18150201705 06. Md. Emran Hossain M18150201706
- 4. PRESENTATION TOPIC “Business Mathematics is a very powerful tool and analytical process that results in and offers an optimal solution , in spite of its limitations”
- 5. What is mathematics? Mathematics is the science that deals with the logic of shape, quantity and arrangement. Math is all around us, in everything we do. It is the building block for everything in our daily lives, including mobile devices, architecture (ancient and modern), art, money, engineering, and even sports. Limitations of Mathematics Rigidity So expensive to use tools for compulsion Delicacy or coarseness
- 6. PRESENTER SOUROV SHAHA SUVO ID: M18150201705 TOPIC: NUMBER SYSTEM
- 7. NUMBER SYSTEM In mathematics, a number system is a set of numbers. In business mathematics, numbers are used for solving business problems.
- 8. FLOW CHART OF NUMBER SYSTEM Number System Real Numbers Rational Integers Negative Odd Even Non negative Zero Positive Natural Prime Composite Fractions Decimal Terminative Non terminative Fractional Irrational Imaginary Numbers Positive Negative
- 9. NUMBER SYSTEMS The Natural Numbers All positive whole numbers are called natural numbers. That is all positive integer except zero are called natural numbers. The Integers All whole numbers negative positive and including zero are known as integer numbers. ex: {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}. Real Number A real number is a combination of rational & irrational number. Ex: 10, -10, ½, 0.
- 10. TYPES OF NUMBER SYSTEMS The Rational Numbers The number which can be expressed in the form p/q where p & q are two integer but q is not equal 0 is called rational number. The Irrational Numbers The number which cannot be expressed in the form p/q where p & q are two integer but q is not equal 0 is called irrational number. Imaginary Number Square roots of negative numbers are called imaginary numbers. Ex: Complex Number Combination of real and imaginary numbers are called complex number. Ex: 4+5i 2
- 12. INDICES Indices Indices are a useful way of more simply expressing large numbers. They also present us with many useful properties for manipulating them using what are called the Law of Indices. We call "2" the base and "5" the index.
- 13. LOGARITHMS Logarithms Discovered by the Scottish Laird, John Napier of Merchiston. He was a mathematician, astronomer, astrologer and physicist. He introduced logarithms as a way to simplify calculations.
- 14. LOGARITHM Natural logarithm: When base ‘e’ then the logarithm function is called natural logarithm function. Example: Log e^3 Common logarithm: When base is 10, and then it is called common logarithm. Example: log 10^3
- 15. SET THEORY Definition A set is a collection of well defined and well distinguished objects. The basic characteristics of a set is that - It should be well defined. Elements should be well distinguished Easy recognition and description
- 16. PROPERTIES OF SET Sub-sets A is a subset of B if every element of A is also contained in B. This is written For example, the set of integers { …-3, -2, -1, 0, 1, 2, 3, …} is a subset of the set of real numbers. means if Empty set Set with no elements { } or Ø. BA BA bthenxAx ,
- 17. PROPERTIES OF SET (CONT.) Proper subset Set B is called proper subset of super set A if each and every element of set B are the elements of the set A and at least one element of superset A is not an element of B. ex: Let, A = {1,2,3,4,5,6,7} B = {1,3,5,7} So, Venn Diagram A Venn diagram is a pictorial representation. It was named after English logician John Venn. AB
- 18. SET OPERATORS Union of two sets A and B is the set of all elements in either set A or B. Written A U B Intersection of two sets A and B is the set of all elements in both sets A or B. Written A ∩ B Difference of two sets A and B is the set of all elements in set A which are not in set B. Written A - B. Complement of a set is the set of all elements not in the set. Written Need a universe of elements to draw from. Set U is usually called the universal set. }:{ BAorxxxBA }:{ BAandxxxBA }:{ BAandxxxBA A }:{ AUxxA
- 19. PRESENTER MD. EMRAN HOSSAIN ID: M18150201706 TOPIC: EQUATION
- 20. EQUATION Equation is a mathematical statement that uses the equal sign to show that the two expressions are equal. The equity is true only for certain value or values symbolized generally by x,y,z etc. for example: The equation: 3x+5=2x+7 is true for x=2 but not for x=3.
- 21. CLASSIFICATION Linear Equation Non-linear Equation A linear equation is an equation for a straight line. It is made up of two expressions equal to each other. For example, “y=2x+1” Equation whose graph doesn’t form a straight line is called a non-linear equation the variables are either of degree greater than 1 or less than 1 but never 1. For example, 01 2 xx
- 22. CLASSIFICATION Linear Equation Non-linear Equation
- 23. EQUATION Quadratic equation A quadratic equation is one that can be written in the standard form of ax2+bx+c=0. Where a , b and c are real number and a is not equal to zero. And the highest power of quadratic equation is 2. For example, Cubic equation An equation of third is called cubic equation. The general degree form of a cubic equation is A cubic equation has three possible values of its variable and at least one of them is real number. For example, Bio-quadratic equation Bio-quadratic equation is a type of equation which relates to the fourth degree of power and does not contain any terms of the third or first power. for example, 0297 2 xx 02 cbxax 023 dcxbxax 07126 23 xxx 045 24 xx
- 24. EQUATION (CONT.) Identity: An identity is true any value of the variable. For example, a2+2ab+b2= ()2 Variable: A variable is a symbol for number we don’t know. Generally it is written as x,y,z etc. Inequality: An inequality is a mathematical sentence in which two expressions are joined by relations symbols such as (not equal to), > (greater than), < (less than), (greater than or equal to), (less than or equal to). Examples of inequalities are, • a>b : a is greater than b • a<b : a is less than b 222 )(2 bababa
- 25. PRESENTER MD. AKASHUR RAHMAN ID: M18150201702 TOPIC: PERMUTATION & COMBINATION
- 26. PERMUTATIONS A permutation is an arrangement of all or part of a set of objects, with regard to the order of the arrangement. Permutation is an ordered arrangement of items that occurs when: No item is used more than once. The order of arrangement makes a difference. Ex: Let 1,2,3 be three number and their all possible permutations will be (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), and (3,2,1). There are two types of Permutation. i. Repetitive ii. Non-repetitive Arrangement Variation Order
- 27. COMBINATIONS A combination is a way of selecting several things out of a larger group where (unlike permutations) order does not matter. Arrangement is not important The items are selected from the same group. No item is used more than once. The order of items makes no difference. Example: You are making a sandwich. How many different combinations of 2 ingredients can you make with cheese, mayo and ham? Answer: {cheese, mayo}, {cheese, ham} or {mayo, ham}.
- 28. PERMUTATIONS VS. COMBINATIONS Permutations Combinations Defined as different ways of arranging r objects out of given n objects in a particular order. Defined as selecting r objects out of n objects where order of the objects does not matter. Represents arrangement. Represents grouping / selection. Arrangements of n items taken r at a time. Subsets of n items taken r at a time. Order is important. Order is not important. Denoted by nPr Denoted by nCr Clue words: arrangement, schedule, order. Clue words: group, sample, selection.
- 29. APPLICATIONS Permutations and combinations come handy, in more or less prominent ways, in almost every area of practical mathematics. They often arise when different orderings on certain finite sets are considered, possibly only because one wants to ignore such orderings and needs to know how many configurations are thus identified. Area of applications : Computer architecture Computational molecular biology Operations research Simulation Homeland security Accumulation of electronic communication data
- 30. REMARKS 1. Use permutations if a problem calls for the number of arrangements of objects and different orders are to be counted. 2. Use combinations if a problem calls for the number of ways of selecting objects and the order of selection is not to be counted.
- 32. ARITHMETIC PROGRESSION An arithmetic progression is a sequence whose terms increase or decrease by a constant number.
- 33. GEOMETRIC PROGRESSION A geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio ½.
- 34. MATHEMATICS OF FINANCE Present Value (PV) Present value describes how much a future sum of money is worth today. • The formula for present value is: Future value (FV) Refers to a method of calculating how much the present value (PV) of an asset or cash will be worth at a specific time in the future. • The formula for present value is: Simple interest A quick method of calculating the interest charge on a loan. Simple interest is determined by multiplying the interest rate by the principal by the number of periods. n rFVPV )1/( n rPVFV )1(
- 35. MATHEMATICS OF FINANCE Compound Interest Interest which is calculated not only on the initial principal but also the accumulated interest of prior periods. Compound interest differs from simple interest in that simple interest is calculated solely as a percentage of the principal sum. The equation for compound interest is: Amortization Amortization is a method of spreading the cost of an intangible asset over a specific period of time, which is usually the course of its useful life. Intangible assets are non- physical assets that are nonetheless essential to a company, such as patents, trademarks, and copyrights. The goal in amortizing an asset is to match the expense of acquiring it with the revenue it generates. nt n r CP )1(
- 36. MATHEMATICS OF FINANCE Annuity A regular periodic payment made by an insurance company to a policyholder for a specified period of time. Need of Annuities 1. The payment of tax is deferred 2. Annuity provides large amount which is more helpful for retiring persons 3. The annuity income and payments are guaranteed
- 38. MATRICES Matrices, a set of numbers arranged in rows and columns so as to form a rectangular array. The numbers are called the elements, or entries, of the matrices. A matrix is a two dimensional array of numbers or terms arranged in a set of rows and columns. An matrix has m rows and n columns. An element aij located in the "i" the row and the 'j' the column. Business Application of Matrices: In business very large matrices are used for optimization of problems, for example in making the best use of assets, whether labor or capital, in the manufacturing of a product and managing very large supply chains.
- 39. TYPES OF MATRICES • Rectangular Matrix • Square Matrix • Row Matrix • Column Matrix • Diagonal Matrix • Scalar Matrix • Unit Matrix or Identity Matrix • Zero Matrix or Null Matrix
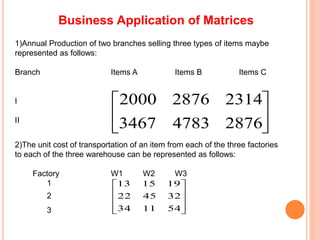
- 40. Business Application of Matrices 1)Annual Production of two branches selling three types of items maybe represented as follows: Branch Items A Items B Items C I II 2)The unit cost of transportation of an item from each of the three factories to each of the three warehouse can be represented as follows: Factory W1 W2 W3 1 2 3 287647833467 231428762000 541134 324522 191513
- 41. Example An automobile dealer sells two car models, standard and deluxe. Each is available in one of the two colors, white and red. His shakes for the month of January and February are given by the matrices. Standard Deluxe A= B= 43 12 32 13 Find the total sales for each models and color for both models. Solution: By adding A and B we can get the total sales for each models and color for both models. A+B= + = Answer: The total sales for each models and color for both models is 43 12 32 13 75 25 75 25
- 42. DIFFERENTIATION In mathematics, Differentiation is the process of finding the derivative, or rate of change, of a function.. Differentiation also allows us to find the rate of change of x with respect to y. If y = some function of x (in other words if y is equal to an expression containing numbers and x’s), then the derivative of y (with respect to x) is written by example: if dx dy 1 1 , , nn nn nkx dx dy kxy nx dx dy xy
- 43. BUSINESS APPLICATION OF DIFFERENTIATION Total costs (TC): Total cost is the combination of fixed cost and variable cost of output. Total revenue (TR): Total revenue is the product of price/demand function and output. Profit: Profits are defined as the excess of total revenue over total costs. Symbolically it can be expressed as, P (profit) = TR – TC. i.e., (Total Revenue – Total Cost). Marginal Cost (MC): MC is the extra cost for producing one additional unit when the total cost at certain level of output is known. Hence, it is the rate of change in total cost with respect to the level of output at the point where total cost is known. Marginal Revenue (MR): MR is defined as the change in the total revenue for the sale of an extra unit. Hence, it is the rate of change total in revenue with respect to the quantity demanded at the point where total revenue is known in level of output is known.