Ch05

컴파일러 입문
제 5 장
Context-Free 문법

목 차
5.1 서론
5.2 유도와 유도 트리
5.3 문법 변환
5.4 CFG 표기법
5.5 푸시다운 오토마다(PDA)
Context-free Grammar Page 2

5.1 서론
 regular expression: the lexical structure of tokens
 recognizer : FA( scanner)
 id = l(l + d)*
, sc = ´(c + ´´)*
´
 CFG: the syntactic structure of programming languages
 recognizer : PDA( parser)
 프로그래밍 언어의 구문 구조를 CFG로 표현할 경우의
장점:
1. 간단하고 이해하기 쉽다.
2. CFG로부터 인식기를 자동으로 구성할 수 있다.
3. 프로그램의 구조를 생성규칙에 의해 구분할 수 있으므로
번역시에 유용하다.

 CFG의 form : N. Chomsky의 type 2 grammar
A  , where A  VN and   V*
.
 문법기호들의 notational convention
 1. Terminal symbol
 (1) a, b, c 등 알파벳 시작부분의 소문자와 숫자 0, 1, 2, ⋯
 (2) +, - 연산자와 semi-colon, comma, 괄호 등 delimiter
 (3) ‘if’, ‘then’과 같이 인용부호 사이에 표기된 문법기호
 2. Nonterminal symbol
 (1) A, B, C 등 알파벳 시작부분의 대문자
 (2) S는 보통 시작기호로 사용
 (3) <stmt>, <expr>과 같이 <와 >로 묶어서 나타낸 문법기호

 3. 만약 아무런 언급이 없으면 첫번째 생성규칙의 LHS 기호가
시작기호임.
 4. A → 1, A → 2, ⋯, A → k와 같이 생성규칙의 LHS가 모두
A인 경우에 A → 1 |2 | ⋯ | k로 간단히 표기할 수 있다.
 → A에 대한 택일(alternation) 규칙
 형식언어 이론에서 사용하는 각 기호들의 의미
 1. X, Y, Z와 같은 알파벳 끝부분의 대문자는 보통 문법기호, 즉
nonterminal 혹은 terminal 기호를 나타낸다(X,Y,Z∈V).
 2. 알파벳 끝부분의 소문자, 주로 u, v, ⋯, z는 terminal들로 이루
어진 string을 나타낸다. 역시 terminal string을 나타내는 대표
적인 문자이다( ∈VT
*
).
 3. , , 와 같은 그리스체 소문자는 문법기호로 구성된 string을
나타낸다( , , ∈V*
).

 recursive construction
ex) E  E OP E | (E) | -E | id
OP   |  |  | /
VN =  E, OP 
VT =  (, ), , id, , , /
ex) <if_statement>  'if' <condition> 'then' <statement>
VN : <와 >사이에 기술된 symbol.
VT : ' 와 ' 사이에 기술된 symbol.

5.2 유도와 유도 트리
 Derivation : 1  2
start symbol로부터 sentence를 생성하는 과정에서 nonterminal
을 이 nonterminal로 시작되는 생성 규칙의 right hand side로 대
치하는 과정.
(1)  : derives in one step.
if A    P, ,   V*
then A  .
(2)  : derives in zero or more steps.
1.   V*
,   
2. if    and    then   
(3)  : derives in one or more steps.
*
**
+
*

 L(G) : the language generated by G
= { | S  ,  ∈ VT*}
 definition :
sentence : S  ,   VT*  모두 terminal로만 구성.
sentential form : S  ,   V*.
*
*
*

 다시 말하면 CFG에서 문장의 생성은 유도 과정으로 말할 수 있고
문장형태(sentential form)의 string에서 생성규칙을 반복적으로
적용하여 nonterminal을 확장
 예) 산술식을 나타내는 문법
 E → E+E | E*E | (E) | -E | id(5・1)
 -(id)의 유도 : E ⇒ -E ⇒ -(E) ⇒ -(id)
 CFG에서는 생성규칙의 RHS에 nonterminal이 여러 개 올 수 있으
므로 같은 문장을 유도하는 과정이 여러 개 있을 수 있다. 즉, 문
장형태에서 유도시 대치해야 할 nonterminal을 선택하는데 여러
가지 경우가 있을 수 있다.

 Choosing a nonterminal being replaced
 sentential form에서 어느 nonterminal을 선택할 것인가 ?
A   , where   V*.
leftmost derivation: 가장 왼쪽에 있는 nonterminal을 대치해
나가는 방법.
rightmost derivation: 가장 오른쪽에 있는 nonterminal을 대치.
 A derivation sequence 0  1  ...  n is called a
leftmost derivation if and only if i+1 is obtained from i
by applying a production to the leftmost nonterminal in i
for all i, 0  i  n-1.
i  i+1 : 가장 왼쪽에 있는 nonterminal을 차례로 대치.

 예3) 문장 -(id+id)가 문법 (5・1)에 의해 유도되는 과정
 (1) 좌단유도
 E ⇒ -E ⇒ -(E) ⇒ -(E+E) ⇒ -(id+E) ⇒ -(id+id).
 (2) 우단유도
 E ⇒ -E ⇒ -(E) ⇒ -(E+E) ⇒ -(E+id) ⇒ -(id+id).
 parse : parser의 출력 형태 중에 한가지.
 left parse : leftmost derivation에서 적용된 생성 규칙 번호.
 top-down parsing
 start symbol로부터 sentence를 생성
 right parse : rightmost derivation에서 적용된 생성 규칙 번호의 역순.
 bottom-up parsing
 sentence로부터 nonterminal로 reduce되어 결국엔 start symbol로
reduce.

 문장 a+a*a의 left parse와 right parse를 구하시오.
 1. E → E+T 2. E → T 3. T → T*F 4. T → F
5. F → (E) 6. F → a
left parse: 1 2 4 6 3 4 6 6. right parse: 6 4 2 6 4 6 3 1.
E ⇒ E+T (1) E ⇒ E+T (1)
⇒ T+T (2) ⇒ E+T*F (3)
⇒ F+T (4) ⇒ E+T*a (6)
⇒ a+T (6) ⇒ E+F*a (4)
⇒ a+T*F (3) ⇒ E+a*a (6)
⇒ a+F*F (4) ⇒ T+a*a (2)
⇒ a+a*F (6) ⇒ F+a*a (4)
⇒ a+a*a (6) ⇒ a+a*a (6)
Introduction to Compiler Design Theory Page 12

유도 트리
::= a graphical representation for derivations.
::= the hierarchical syntactic structure of sentences that is implied by the
grammar.
 Definition : derivation tree
CFG G = (VN,VT,P,S) &   VT
*
 drawing a derivation tree.
1. nodes: symbol of V(VN  VT)
2. root node: S(start symbol)
3. if A  VN, then a node A has at least one descendent.
4. if A  A1A2...An  P, then A가 subtree의 root가 되고 좌로부터
A1,A2,...,An가 A의 자 노드가 되도록 tree를 구성
A1 A2
A
‥‥ An

≠
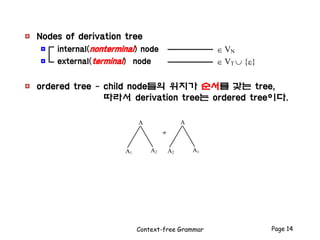
A1 A2
A
A2 A1
A
 Nodes of derivation tree
 internal(nonterminal) node  VN
 external(terminal) node  VT  {}
 ordered tree - child node들의 위치가 순서를 갖는 tree,
따라서 derivation tree는 ordered tree이다.

예) G : E → E + T | T
T → T * F | F
F → ( E ) | a
 : a + a * a
스트링 a + a * a의 유도 트리:
+
T
F
T F
E
aF
E
T
*
a a
※ 각각의 유도 방법에 따
라 derivation tree 모양은
변하지 않는다. 즉, 한 문
장에 대한 tree 모양은
unique하다.

Ambiguous Nondeterministic
(X)
(O)
 Ambiguous Grammar
 A context-free grammar G is ambiguous if and only if it
produces more than one derivation trees for some sentence.
 설명: 같은 sentence를 생성하는 tree가 2개 이상 존재할 때
이 grammar를 ambiguous하다고 하며, 결정적인 파싱을
위해 nondeterministic한 grammar를 deterministic하게
변환해야 한다.
nondeterministic

 문장 a+a*a의 left parse와 right parse를 구하시오.
 1. E → E+E 2. E → E*E 3. E → (E) 4. E→ a
left parse: 1 2 4 6 3 4 6 6. right parse: 6 4 2 6 4 6 3 1.
E ⇒ E+E (1) E ⇒ E*E (1)
⇒ a+E (4) ⇒ E+E*E (2)
⇒ a+E*E (2) ⇒ a+E*E (4)
⇒ a+a*E (4) ⇒ a+a*E (4)
⇒ a+a*a (4) ⇒ a+a*a (4)
a
a a
*
+
EE
E
E
E
a
a a
+
*
EE
E
E
E
ambiguous

S
thenCif elseS S
thenCifb S
b a
a
1)
S
thenCif S
thenCifb S else
b a
S
a
2)
 “G: ambiguous 증명”  하나의 sentence로 부터 2개 이상의
derivation tree 생성.
ex) dangling else problem:
G: S  if C then S else S | if C then S | a
C  b
: if b then if b then a else a
※ else : 일반적으로 right associativity를 만족한다.
if 문장의 경우 자신과 가장 가까운 if와 결합함으로
두개의 트리 중 일반적으로 2)를 만족.

 In a more general form, the ambiguity appears when there is a
production of the following form.
 production form : A  AA
 sentential form : AAA
 tree form :
 모호성 제거
 ① 가 좌측결합(left associative) 연산자인 경우
A → A A' | A', A' → 
 ② 가 우측결합(right associative) 연산자인 경우
A → A' A| A', A' → 
or
A
A α A
A α A A α A
A
A α A

 ambiguous  unambiguous
1) 새로운 nonterminal을 도입해서 unambiguous grammar로 변환.
2) 이 과정에서, precedence & associativity 규칙을 이용.
 nondeterministic  deterministic
예) G : E  E  E | E + E | a
 : a  a + a
 precedence rule의 적용
a +
1) + > *
a
E
E * E
E E
a
*
+
E E
E E
E
a
aa
2) * > +

 새로운 nonterminal의 도입
G : E  E + T | T
T  T * F | F
F  a
+
T
F
T F
E
aF
E
T
*
a a
※ 그런데, grammar의 ambiguity를
check할 수 있는 algorithm이
존재하지 않으며 unambiguous하게
바꾸는 formal한 방법도 존재하지
않는다.

 unambiguous grammar로 바꾼 예:
 최초 문법
 E → E+E | E-E | E*E | E/E | E↑E | -E | (E) | id
 우선 순위 : +, - ≺ *, / ≺ ↑ ≺ -(unary)
 수정된 문법
G : expression  expression + term
┃ expression - term
┃ term
term  term * factor
┃ term / factor
┃ factor
factor  primary ↑ factor
┃ primary
primary  - primary
┃ element
element  ( exp )
┃ id
 derivation tree가 하나이므로 위 grammar는 unambiguous하다.

 id * id + id의 derivation tree:
 derivation tree가 하나 이므로 위 grammar는 unambiguous하다.
expression
expression expression
term factor
term factor
factor primary
primary element
element id
id
primary
element
id
+
+

5.3 문법 변환
Introduction
5.3.1 Useless Productions
5.3.2 -Productions
5.3.3 Single productions
5.3.4 Canonical Forms of Grammars

5.3 Introduction
 Given a grammar, it is often desirable to modify the grammar so
that a certain structure is imposed on the language generated.
 grammar transformations without disturbing the
language generated.
 Definition :
Two grammars G1 and G2 are equivalent
if L(G1) = L(G2).
 예8) 다음 CFG G1과 G2는 동일하다.
G1 : A → 1B G2 : X → Y1 ∴L(G1) = L(G2) = 1(01)*
A → 1 X → 1
B → 0A Y → X0

 Two techniques
 Substitution :
if A  B, B  1 | 2 | 3 … | n P, then
P' = ( P - {A  B } )  {A  1 | 2 | ... | n }.
 Expansion :
A   <=> A  X, X   or A  X, X  
 All grammars can be transformed the equivalent
grammars through the substitution and expansion
techniques.

 예9) S → aT | bT, T → S | Sb | c 에서
생성규칙 S→ aT 를 제거하시오.
 S → aT | bT 에 T → S | Sb | c 대입
 S → aS | aSb | ac | bT
 결과 = S → aS | aSb | ac | bT , T → S | Sb | c

5.3.1 Useless Productions
 A useless production in a context-free grammar is
one which can not be used in the generation of a
sentence in the language defined by the grammar.
 it can be eliminated.
 Definition : We say that a symbol X is useless if
not ∃S  Xy  xy, ,x,y  VT
*
.
**

 Splitting up into two distinct problems:
 Terminating nonterminal :
A   ,   , where A  VN and   VT
*
.
 Accessible symbol :
S  X, where X ∈ V and ,  V*
.
 An algorithm to remove useless productions will
involve computing the terminating nonterminals
followed by the accessible symbols.
*
*

 Terminating nonterminal을 구하는 방법:
Algorithm terminating;
begin
VN':= { A | A   ∈ P,  ∈ VT
*
};
repeat
VN' := VN' ∪ { A | A   ∈ P, ∈ (VN' U VT )*
}
until no change
end.
 Accessible symbol을 구하는 방법:
Algorithm accessible;
begin
V ' := { S }; (* initialization *)
repeat
V ' := V ' ∪{ X | some A  X ∈ P, A ∈ V ' }
until no change
end. Context-free Grammar Page 30

 예11) P = { S → A, S → B, B → a } 에서
 1. terminating nonterminal 집합은 ? {B, S}
 2. A는 teminal string을 생성할 수 없으므로 제거하면
P’ = {S → B, B → a }
 예12) P = { S → aB, A → aB, A → aC, B → C, C → b } 에서
 1. Accessible symbol 집합은? {S, a, B, C, b}
 2. 도달 불가능한 심벌을 포함하고 있는 규칙을 제거하면
P’ = { S → aB, B → C, C → b }

 Useless production removal :
 Apply the algorithm for the terminating nonterminal.
 Apply the algorithm for the accessible symbol.
 예13) P = { S → aS, S → A, S → B, A → aA, B→a, C→aa } 에서 불필
요한 생성규칙 제거.
 1. teminating nontermianl ? {C, B, S}
 2. Acessible symbol? {S, a, A, B}
 결과는 P’ = { S → aS, S → B, B→a}
 연습문제 211pg. 5.11 (1)
ex) S  A | B
A  aB | bS | b
B  AB | BB
C  AS | b

5.3.2 -Productions
 Definition :
 We call that a production is -production if the form of the
production is A  , A  VN.
 Definition :
 We say that a CFG G = (VN, VT, P, S ) is  -free if
 P has no -production, or
 There is exactly one -production S   and S does not appear on
the right hand side of any productions in P.

 Conversion to an -free grammar:
Algorithm  -free;
begin
VN := { A | A =>  , A  VN }; (* nullable nonterminal *)
P' := P – { A   | A  VN };
for A  0B11B2... Bkk ∈ P' , where i ≠ and Bi  VN do
if Bi   ∈ P' then
P' = P' ∪ { A  0X1 1X2... Xkk | Xi = Bi or Xi = }
else
P' = P' ∪ { A  0X1 1X2... Xkk | Xi = }
end if
end for
if S  VN then P ' := P ' ∪ { S'   | S }
end.
+

 예14) S → aSbS | bSaS | 
 ① 각 생성규칙에 대하여 제거
S → aSbS ⇒ S → aSbS | aSb | abS | ab
S → bSaS ⇒ S → bSaS | bSa | baS | ba
 ② 시작기호가 으로 생성되면 S' → S | 를 추가
 ex1) A  AaA | ε
 ex2) S  aAbB
A  aA | ε
B  ε

5.3.3 Single productions
 Definition : A  B, where A,B  VN.
 A → B 와 같이 생성규칙의 오른쪽에 한 개의 nonterminal만 오는 경우
⇒ 불필요한 유도과정이 생기며 parsing 속도가 느려진다.
Algorithm Remove_Single_Production;
begin
P' := P – { A  B | A, B  VN};
for each A  VN do
VNA = { B | A  B } ;
for each B  VNA do
for each B    P' do (* not single production *)
P' := P' ∪ { A  α}
end for
end for
end for
end.
+
 main idea : grammar substitution.

 Definition :
A CFG G = ( VN , VT, P, S ) is said to be cycle-free
if there is no derivation of the form A  A for any A in VN.
G is said to be proper if it is cycle-free, is -free, and has no
useless symbols.
+

5.3.4 Canonical Forms of Grammars
 Definition: A CFG G = (VN, VT,P,S) is said to be in Chomsky Normal Form(CNF)
if each production in P is one of the forms
 A  BC with A,B, and C in VN, or
 A  a with a  VT, or
 if   L(G), then S   is a production, and S does not appear on the right side
of any production.
 Conversion to CNF
A → X1 X2....XK, K > 2
⇒ A → X1´<X2 ... XK>
<X2...XK> → X2´<X3 ... XK>
……
<XK-1...XK> → XK-1´XK´, where Xi´= Xi if Xi ∈ VN
add Xi´= Xi if Xi ∈ VT
ex) S →bA
A → bAA | aS | a

 Definition : A CFG G = (VN, VT,P,S) is said to be in
Greibach Normal Form(GNF)
if G is -free and each non--production in P is of the
form A  a with a  VT and   V*.
 Definition : Given any context-free grammar G, we can draw its
dependency graph. The vertices are the terminal and
nonterminal symbols, and the arcs go from A to x if
x appears on the right hand side of a production
whose left hand side is A.
===> It can be used as introducing concepts of algorithms
and the analysis of algorithms(developing algorithms).

5.4 CFG 표기법
☞ BNF(Backus-Naur Form), EBNF(Extended BNF), Syntax Diagram
 BNF
 특수한 meta symbol을 사용하여 프로그래밍 언어의 구문을 명시하는 표기법.
 meta symbol : 새로운 언어의 구문을 표기하기 위하여 도입된 심벌들.
 terminal symbol : ‘ ’
 grammar symbol : VN ∪ VT
 예 : 명칭의 정의
 <id> ::= <letter> | <id><letter> | <id><digit>
 <letter> ::= a | b | c | ⋯ | y | z
 <digit> ::= 0 | 1 | 2 | ⋯ | 8 | 9
nonterminal symbol < >
 ::= (치환)
nonterminal symbol의 rewriting | (또는)

예1) VN = {S, A, B}, VT = {a, b}
P = {S  AB, A  aA, A  a, B  Bb, B  b}
 BNF 표현:
<S> ::= <A> 
<A> ::= a <A> | a
 ::= b | b
예2) Compound statement
 BNF 표현:
<compound_statement> ::= ‘{’<statement_list> ‘}’
<statement_list> ::= <statement_list> <statement>
| <statement>
<S> ::= <A> 
<A> ::= ' a ' <A> | ' a '
 ::= ' b ' | ' b '

 Extended BNF(EBNF)
 특수한 의미를 갖는 meta symbol을 사용하여 반복되는 부분이나
선택적인 부분을 간결하게 표현.
 meta symbol
 ex.
 ① BNF : <id_list> ::= <id_list>, <id> | <id>
 ② EBNF --- 반복되는 부분을 {}로 표현 : <id_list> ::= <id> {, <id> }
 예) 계산식
 ① BNF : <exp> ::= <exp> + <exp> | <exp> - <exp> | <exp>  <exp> | <exp> / <exp>
 ② EBNF : <exp> ::= <exp> (  |  |  | / ) <exp>
 예) <if-st> ::= 'if' ‘(’ <expression> ‘)’ <statement> [‘else’ <statement>]
반복되는 부분(repetitive part): { }
선택적인 부분(optional part): [ ]
괄호와 택일 연산자(alternative): ( | )

 예18) compound statement의 CFG 표현
 ① BNF
 <compound_statement> ::= begin <statement_list> end
 <statement_list> ::= <statement_list>; <statement> | <statement>
 ② EBNF --- 반복되는 부분을 {}, 선택은 []로 표현
 <compound_statement> ::= begin <statement> {; <statement>} end
 예19) 단순변수와 1차원 배열에 대한 BNF와 EBNF
 ① BNF : <variable> ::= <id> | <id> '[' <exp> ']'
 ② EBNF : <variable> ::= <id> [ '[' <exp> ']' ]
 ※ EBNF에서 사용되는 meta symbol들을 terminal로 사용할 때는 ‘’로 묶어 표현
 예20) production rule을 EBNF로 변환
 <BNF_rule> ::= <left_part> ‘::=‘ <right_part>
 <right_part> ::= <right_part_element> { ‘|’ <right_part_element>}
 pg. 187 Mini C의 문법의 EBNF

 Syntax diagram
 초보자가 쉽게 이해할 수 있도록 구문 구조를 도식화하는 방법
 syntax diagram에 사용하는 그래픽 아이템:
원 : terminal symbol
사각형 : nonterminal symbol
화살표 : 흐름 경로
 syntax diagram을 그리는 방법:
1. terminal a
2. nonterminal A
a
A

3. A ::= X1X2... Xn
(1) Xi가 nonterminal인 경우:
(2) Xi가 terminal인 경우:
4. A ::= 1┃2┃...┃ n
X1 Xn····A X2
X1 Xnz ····A X2
α1
α2
.
.
.
αn
A

5. EBNF A ::= {}
6. EBNF A ::= []
7. EBNF A ::= (1┃2)
α
A
A
α
α1
α2
βA

(예) A ::= a | (B)
B ::= AC
C ::= {+A} A CB
A
C
+
A
( B )
α
A
( A )
α
A +

5.5 Push-Down Automata
 finite automata의 제약
 기억장소가 없으므로 처리된 input symbol의 수를 헤아릴 수 없음
 CFG의 인식기 Push-Down Automata
 push-down list(stack), input tape, finite state control
a1 a2 ··· ai ··· an
Finite State Control
Z1
Z2
:
Zn
Stack
: input tape

 Definition: PDA P = (Q, , , , q0, Z0, F),
where, Q : 상태 심벌의 유한 집합.
 : 입력 알파벳의 유한 집합.
 : 스택 심벌의 유한 집합.
 : 사상 함수 Q  ( ∪{})    Q  *,
q0 ∈ Q : 시작 상태(start state),
Z0 ∈ F : 스택의 시작 심벌,
F ⊆ Q : 종결 상태(final state)의 집합이다.
  : Q  ( ∪ {})    Q  *
 (q,a,Z) ={(p1, 1), (p2, 2), ... ,(pn, n)}
 의미: 현재 상태가 q이고 입력 심벌이 a이며 스택 top 심벌이 Z일 때,
다음 상태는 n개 중에 하나이며
만약 (pi, i)가 선택되었다면 그 의미는 다음과 같다.
 현재의 q 상태에서 입력 a를 본 다음 상태는 pi이다.
 스택 top 심볼 Z를 i로 대치한다.

 P의 configuration : (q, , )
where, q : current state
 : input symbol
 : contents of stack
 P의 이동(move)ː┣
 (q’, )  (q,a,Z) 라면
 a   : (q, a, Z) ┣ ( q', , )
 a =  : (q, , Z) ┣ (q', , ) <===> -move
※ ┣ : zero or more moves, ┣ : one or more moves
 L(P) : the language accepted by PDA P.
 start state : (q0, , Z0)
 final state : (q, , α), where q ∈ F,  ∈ *
L(P) = {ω | (q0, , Z0) ┣ (q, , ), q ∈ F,  ∈ * }.
*
+
+

ex) P = ({q0, q1, q2}, {0, 1}, {Z, 0}, , q0, Z, {q0}),
where, (q0, 0, Z) = {(q1, 0Z)} (q1, 0, 0) = {(q1, 00)}
(q1, 1, 0) = {(q2, )} (q2, 1, 0) = {(q2, )}
(q2, , Z) = {(q0, )}
 스트링 0011의 인식 과정:
(q0, 0011, Z)
┣ (q1, 011, 0Z)
┣ (q1, 11, 00Z)
┣ (q2, 1, 0Z)
┣ (q2, , Z)
┣ (q0, , )
• 스트링 0n1n(n≥1)의 인식 과정:
(q0, 0n1n, Z)
┣ (q1, 0n-11n, 0Z)
┣ n-1 (q1, 1n, 0nZ)
┣ (q2, 1n-1, 0n-1Z)
┣ n-1 (q2, , Z)
┣ (q0, , )
∴ L(P) = {0n1n | n  1}.

 확장된 PDA
δ : Q × (∪{}) × * → Q × *
 한번의 move로 stack top 부분에 있는 유한 길이의 string을 다른 string으로 대치.
(q, a, ) ┣ (q', , )
 stack이 empty일 때도 move가 발생
예) PDA = ({q0, qf}, {a, b}, {a, b, S, Z}, , q0, Z, {qf})
where, (q0, a, ) = {(q0, a)}
(q0, b, ) = {(q0, b)}
(q0, , ) = {(q0, S)} ※ S : center mark
(q0, , aSa) = {(q0, S)}
(q0, , bSb) = {(q0, S)}
(q0, , SZ ) = {(qf, )}

 스트링 aabbaa의 인식 과정:
(q0, aabbaa, Z) ┣ (q0, abbaa, aZ)
┣ (q0, bbaa, aaZ)
┣ (q0, baa, baaZ)
┣ (q0, baa, SbaaZ)
┣ (q0, aa, bSbaaZ)
┣ (q0, aa, SaaZ)
┣ (q0, a, aSaaZ)
┣ (q0, a, SaZ)
┣ (q0, , aSaZ)
┣ (q0, , SZ)
┣ (qf, , )
∴ L = { R
|  ∈ {a, b}+
}.
예) PDA = ({q0, qf}, {a, b},
{a, b, S, Z}, , q0, Z, {qf})
where, (q0, a, ) = {(q0, a)}
(q0, b, ) = {(q0, b)}
(q0, , ) = {(q0, S)}
(q0, , aSa) = {(q0, S)}
(q0, , bSb) = {(q0, S)}
(q0, , SZ ) = {(qf, )}

 Le(P) : stack을 empty로 만드는 PDA에 의해 인식되는 string의 집합.
즉, 입력 심벌을 모두 보고 스택이 empty일 때만
인식되는 string의 집합.
∴ Le(P) = {  ┃ (q0, , Z0) ┣ (q, , ), q ∈ Q} .
 Le(P’) = L(P)인 P’의 구성: (text p. 202)
P = (Q, , , , q0, Z0, F)
===> P’ = (Q∪{qe, q’},  , ∪{Z’}, ’, q’, Z’,  ),
where ’ : 1) 모든 q ∈ Q, a ∈ ∪{}, Z ∈  에 대해,
’(q, a, Z) = (q, a, Z).
2) ’(q’, , Z’) = {(q0, Z0Z’)}. Z’ : bottom marker
3) 모든 q ∈ F, Z ∈ ∪{Z’}에 대해, ’(q, , Z)에 (qe, )를 포함.
4) 모든 Z ∈ ∪{Z’}에 대해, ’(qe, , Z) = {(qe, )}
*

5.6 Context-free 언어와 PDA 언어
 a language is accepted by a PDA if it is a context-free
language.
 CFG <===> PDA
 CFG ===> PDA (for a given context-free grammar,
we can construct a PDA accepting L(G).)
 Top-Down Method
 leftmost derivation, A  
 Bottom-Up Method
 rightmost derivation,  ==>A
 PDA ===> CFG

 Top-Down Method
 CFG G로부터 Le(R)=L(G)인 PDA R의 구성
 For a given G = (VN, VT, P, S),
construct R = ({q}, VT, VN∪ VT, , q, S,  ),
where  : 1) if A  ∈ P, then (q,,A)에 (q,)를 포함 .
2) a ∈ VT에 대해, (q, a, a) = {(q, )}.
ex) G = ({E, T, F}, {a, , +, (, )}, P, E),
P : E  E + T | T
T  T  F | F
F  (E) | a
===> R = ({q}, , , , q, E, )
where  : 1) (q, , E) = {(q, E + T), (q, T)}  expand
2) (q, , T) = {(q, T  F), (q, F)}
3) (q, , F) = {(q, (E)), (q, a)}
4) (q, t, t) = {(q, )}, t∈{a, +, , (, )}  pop

 스트링 a + a  a의 인식 과정:
(q, a + a  a, E) ┣ (q, a + a  a, E + T)
┣ (q, a + a  a, T + T)
┣ (q, a + a  a, F + T)
┣ (q, a + a  a, a + T)
┣ (q, + a  a, + T)
┣ (q, a  a, T)
┣ (q, a  a, T  F)
┣ (q, a  a, F  F)
┣ (q, a  a, a  F)
┣ (q,  a,  F)
┣ (q, a, F)
┣ (q, a, a)
┣ (q, , )
※ 스택 top은 세 번째 구성 요소의 왼쪽.
R = ({q}, , , , q, E, )
where  : 1) (q, , E) = {(q, E + T), (q, T)}
2) (q, , T) = {(q, T  F), (q, F)}
3) (q, , F) = {(q, (E)), (q, a)}
4) (q, t, t) = {(q, )}, t∈{a, +, , (, )}.
ex) G = ({E, T, F}, {a, , +, (, )}, P, E),
P : E  E + T | T
T  T  F | F
F  (E) | a

 Bottom-Up Method
 CFG ===> extended PDA(rightmost derivation)
 R = ( {q, r}, VT, VN∪VT, , q, $, {r} )
 (1) A→ ∈ P 이면, (q, , )에 (q, A)를 추가
 (2) 모든 a∈VT에 대하여, (q, a, ) = { (q, a) }
 (3) (q, , $S) = { (r, ) }
===> R = ({q, r}, VT, VN ∪ VT∪{$}, , q, $, {r})
 : 1) (q, t, ) = {(q, t)}, t ∈{a, +, , (, )}
 shift
2) (q, , E + T) = {(q, E)}
(q, , T) = {(q, E)}
(q, , T * F) = {(q, T)}
(q, , F) = {(q, T)}
(q, , (E)) = {(q, F)}
(q, , a) = {(q, F)}
 reduce
3) (q, , $E) = {(r, )}
ex) G = ({E, T, F}, {a, , +, (, )}, P, E),
P : E  E + T | T
T  T  F | F
F  (E) | a

 스트링 a + a  a의 인식 과정
(q, a + a  a, $) (q, + a  a, $ a)
┣ (q, + a  a, $ F)
┣ (q, + a  a, $ T)
┣ (q, + a  a, $ E)
┣ (q, a  a, $ E +)
┣ (q,  a, $ E + a)
┣ (q,  a, $ E + F)
┣ (q,  a, $ E + T)
┣ (q, a, $ E + T )
┣ (q, , $ E + T  a)
┣ (q, , $ E + T  F)
┣ (q, , $ E + T)
┣ (q, , $ E)
┣ (r, , )
※ 스택 top은 세 번째 구성 요소의 오른쪽.
R = ({q, r}, VT, VN ∪ VT∪{$}, , q, $, {r})
 : 1) (q, t, ) = {(q, t)}, t ∈{a, +, , (, )}
2) (q, , E + T) = {(q, E)}
(q, , T) = {(q, E)}
(q, , T * F) = {(q, T)}
(q, , F) = {(q, T)}
(q, , (E)) = {(q, F)}
(q, , a) = {(q, F)}
3) (q, , $E) = {(r, )}
ex) G = ({E, T, F}, {a, , +, (, )}, P, E),
P : E  E + T | T
T  T  F | F
F  (E) | a

 PDA P로부터 L(G) = Le(P)인 CFG G의 구성
Given PDA P = (Q, , , , q0, Z0, F)
===> Construct cfg G = (VN, VT, P, S)
where
(1) VN = {[qZr] | q, r∈Q, Z∈}∪{S}.
(2) VT = .
(3) P : ① (q, a, Z)가 k  1 에 대해 (r, X1... XK)를 가지면
[qZsk]  a[r X1s1][s1X2s2] ... [sk-1Xksk]를 P에 추가.
s1, s2, ..., sk ∈ Q.
② (q, a, Z)가 (r, )를 포함하면 생성규칙
[qZr]  a를 P에 추가.
③ 모든 q ∈ Q에 대해 S  [q0Z0q]를 P에 추가.
(4) S : start symbol.

 결론
 L은 CFG G에 의해 생성되는 언어 L(G)이다.
 L은 PDA P에 의해 인식되는 언어 L(P)이다.
 L은 PDA P에 의해 인식되는 언어 Le(P)이다.
 L은 extended PDA에 의해 인식되는 언어 L(P)이다.

PDA  CFG
ex) P = ({q0, q1, q2}, {0, 1}, {Z, 0}, , q0, Z, {q0}),
where, (q0, 0, Z) = {(q1, 0Z)} (q1, 0, 0) = {(q1, 00)}
(q1, 1, 0) = {(q2, )} (q2, 1, 0) = {(q2, )}
(q2, , Z) = {(q0, )}
 [q0Zs2]  0 [q10s1][s1Zs2] [q10s4]  0 [q10s3][s30s4]
[q10q2] 1 [q20q2] 1 [q2Zq0]  S  [q0Zq0] S  [q0Zq1] S  [q0Zq2]
 VN= {q10q2, q20q2, q2Zq0, q0Zq0, q0Zq1, q0Zq2, S}
 [q0Zs2]  0 [q10s1] [s1Zs2]
q0Zq0 q10q2 q2Zq0
step3 step1 step2
 [q10s4]  0 [q10s3][s10s4]
q10q2 q10q2 q20q2
 VN= {q10q2, q20q2, q2Zq0, q0Zq0, q0Zq1, q0Zq2, S} 에서
B C D A S 로 rename
 S  A A  0BD B  0BC | 1 C  1 D  
S  0A A  0A1 | 1

 L = { R
|  ∈ {a, b}+}를 인식하는 PDA
 PDA = ({q0, q1, q2}, {a, b}, {a, b, z}, , q0, z, {q2})
 (q0, a, z) = {(q0, az)} (q0, b, z) = {(q0, bz)}
(q0, a, a) = {(q0, aa)} (q0, b, a) = {(q0, ba)}
(q0, a, b) = {(q0, ab)} (q0, b, b) = {(q0, bb)}
 (q0, , a) = {(q1, a)} (q0, , b) = {(q1, b)}
 (q1, a, a) = {(q1, )} (q1, b, b) = {(q1, )}
 (q1, , z) = {(q2, z)}

Ch05

More Related Content

Ch05