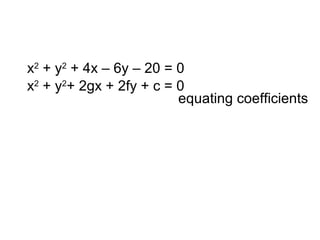Circles getting centre and radius 13
- 1. Block 1 More Circle Stuff
- 2. What is to be learned? • How to get the centre and radius from the equation
- 3. (x – 3)2 + (y + 4)2 = 36 centre (3 , -4) radius 6 x2 + 4x + y2 – 6y = 20 x2 + y2 + 4x – 6y – 20 = 0 (x + 2)2 – 4 + (y – 3)2 – 9= 20 (x + 2)2 + (y – 3)2 = 33 centre (-2, 3) radius √33 x2 + y2 + 4x – 6y – 20 = 0 ÷(-2) √(-2)2 + 32 + 20 rearrange complete square(x + 2)2 + (y – 3)2 = 20 + 4 + 9
- 4. x2 + y2 + 4x – 6y – 20 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients
- 5. x2 + y2 + 4x – 6y – 20 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients
- 6. x2 + y2 + 4x – 6y – 20 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients 2g = 4
- 7. x2 + y2 + 4x – 6y – 20 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients 2g = 4 2f = -6 c = -20 g = 2, f = -3 centre (-2, 3) centre (-g , -f) radius = √(g2 + f2 – c) = √(22 + (-3)2 + 20) = √33
- 8. x2 + y2 + 8x – 4y + 16 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients 2g = 8 2f = -4 c = 16 g = 4, f = -2 centre (-4, 2) centre (-g , -f) radius = √(g2 + f2 – c) = √(42 + (-2)2 – 16) = √4 = 2
- 9. Getting Radius and Centre If given equation of circle it is vital to find centre and radius If no brackets use x2 + y2 + 2gx + 2fy + c = 0 centre (-g , -f) radius = √(g2 + f2 – c)
- 10. x2 + y2 + 8x – 4y – 10 = 0 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients 2g = 8 2f = -4 c = -10 g = 4, f = -2 centre (-4, 2) centre (-g , -f) radius = √(g2 + f2 – c) = √(42 + (-2)2 + 10) = √30
- 11. x2 + y2 – 10x + 2y = 14 x2 + y2 + 2gx + 2fy + c = 0 equating coefficients 2g = -10 2f = 2 c = -14 g = -5, f = 1 centre (5, -1) centre (-g , -f) radius = √(g2 + f2 – c) = √((-5)2 + 12 + 14) = √40 Key Question Find centre and radius x2 + y2 – 10x + 2y – 14 = 0