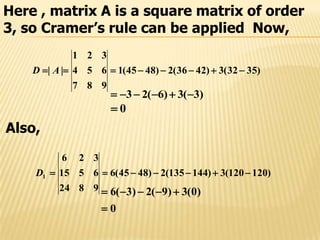Cramer's Rule
- 1. Vector Calculus And Linear Algebra Presented by : Abdul Sattar
- 2. CRAMER'S RULE (Using Determinants to solve systems of equations)
- 3. INTRODUCTION Suppose that we have a square system with n equation in the same number of variables ( ). Then the solution of the system has the following cases. 1) If the system has non-zero coefficient determinant D=det(A), then the system has unique solution and this solution is of the form nxxx ,......., 21 ,,.......,, D D x D D x D D x n n 2 2 1 1 iD th i nbbb ,.....,, 21
- 4. a) if at least one of Di is non-zero then the system has no solution b) if all Di‘s are zero, then the system has infinite number of solutions. In this case, if the given system is homogeneous; that is, right hand side is zero then we have ffollowing possibilities of its solution. 2) If the system has zero coefficient determinant D=det(A) , then we have two possibilities as discussed below.
- 6. EXAMPLE : 1 Find the solution of the system Solution : In matrix form, the given system of equations can be written as Ax=b, where 74 63 52 zyx zyx zyx 7 6 5 ,, 411 113 121 b z y x xA
- 7. Here , matrix A is a square matrix of order 3, so Cramer’s rule can be applied Now, 411 113 121 ||)det( AAD )4(1)11(2)5(1 023 )13(1)112(2)14(1 Therefore, the system has unique solution. For finding unique solution, let us first find D1,D2 and D3 it can be easily verified that )76(1)724(2)14(5 417 116 125 1 D 46 )13(1)17(2)5(5
- 8. EXAMPLE : 2 Find the solution of the system 7242 532 32 zyx zyx zyx Solution : In matrix form, the given system of equations can be written as Ax=b, where 7 5 3 ,, 242 312 121 b z y x xA
- 9. )621(1)112(5)724(1 471 163 151 2 D 23 )15()11(517 )13(5)621(2)67(1 711 613 521 3 D 23 )4(5)15(213 Therefore, the system has unique solution. 1 23 23 ,1 23 23 ,2 23 46 321 D D z D D y D D x
- 10. Here , matrix A is a square matrix of order 3, so Cramer’s rule can be applied Now, )28(1)64(2)122(1 242 312 121 || AD 6)2(210 0 Therefore, either the system has no solution or infinite number of solution. Let us check for it. )720(1)2110(2)122(3 247 315 123 1 D 13)11(2)10(3 05 Therefore, the system has no solution as at least one Di, i=1,2,3 is nonzero.
- 11. EXAMPLE : 3 Find the solution of the system 24987 15654 632 zyx zyx zyx Solution : In matrix form, the given system of equations can be written as Ax=b, where 24 15 6 ,, 987 654 321 b z y x xA
- 12. Here , matrix A is a square matrix of order 3, so Cramer’s rule can be applied Now, )3532(3)4236(2)4845(1 987 654 321 || AD )3(3)6(23 0 Also, )120120(3)144135(2)4845(6 9824 6515 326 1 D 0 )0(3)9(2)3(6
- 13. )10596(3)4236(6)144135(1 9247 6154 361 2 D 0 )9(3)6(69 )3532(6)10596(2)120120(1 2487 1554 621 3 D 0 )3(6)9(20 Therefore, the system has infinitle number of solutions. Now, 0385 54 21
- 14. Therefore, þ(A)=2 Omitting m-r = 3-2 = 1 Considering n-r = 3-2 = 1 variable as arbitary, the remaining system becomes xzy xzy 41565 632 Where x is arbitary Now , 31512 65 32 D 96)415(3)636( 6415 36 1 xxx x x D xxx x x D 3)6(5)415(2 4155 62 1
- 15. Therefore , x x D D zx x D D y 3 3 ,23 3 96 21 Let x = k , where k is arbitary , then the infinite number of solutions of the given system is kzkykx ,23, where k is an arbitary constant.