凸最適化〜双対定理とソルバーCVXPYの紹介〜

凸最適化
双対定理とソルバーCVXPYの紹介
吉田知貴
システム本部 AI システム部データサイエンス第一グループ
株式会社ディー・エヌ・エー
1 / 27

目次
1 凸最適化問題
2 最適化ソルバー
3 ラグランジュ双対問題
4 まとめ
2 / 27

目次
4 まとめ
3 / 27

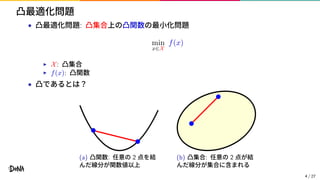
凸最適化問題
• 凸最適化問題: 凸集合上の凸関数の最小化問題
min
x∈X
f(x)
▶ X: 凸集合
▶ f(x): 凸関数
• 凸であるとは？
(a) 凸関数: 任意の 2 点を結
んだ線分が関数値以上
(b) 凸集合: 任意の 2 点が結
んだ線分が集合に含まれる
4 / 27

凸最適化問題の特徴
• 局所解 = 最適解
• 最適性条件が一次式で書ける
Figure: ∇f(x)⊤
(y − x) ≥ 0 for all y ∈ X ⇔ x は最適解
▶ X = Rd
のとき、∇f(x) = 0 ⇔ x は最適解
• 最適化アルゴリズム
▶ 射影勾配法: 勾配法で更新後に凸集合へ射影する
▶ 近接勾配法: 射影勾配法の一般系（もう少し複雑）
▶ 主双対内点法: 制約をバリア関数として扱い主問題と双対問題を同時に解く
5 / 27

目次
4 まとめ
6 / 27

最適化ソルバー
• CVXOPT
▶ 特定の形式の最適化問題を解くことができる
▶ 行列の形式に合わせる必要がある
Figure: https://cvxopt.org/userguide/coneprog.html
• CVXPY ← 今回はこちらを紹介
▶ 自由に目的関数・制約を書くことができる
▶ matlab の CVX の python バージョン（両方 Boyd さんのソフトウェア）
7 / 27

最適化ソルバー CVXPY
• インストール
▶ pip の場合: pip install cvxpy
▶ conda の場合: conda install -c conda-forge cvxpy
• インポート
▶ import cvxpy as cvx
• これから紹介するサンプルは
https://github.com/birdwatcherYT/cvxpy_example にアップしました
8 / 27

例題: 線形計画問題（LP）
min
x
c⊤
x s.t. Ax ≤ b
1 np.random.seed (1)
2 # 次元数
3 m = 3
4 n = 2
5 # 各種定数・変数
6 A = np.random.randn(m, n)
7 b = np.random.randn(m)
8 c = np.random.randn(n)
9 x = cvx.Variable(n) # 変数定義
10 # 問題設定
11 obj = cvx.Minimize(c.T @ x) # 最小化
12 constraint = [A @ x <= b] # 制約
13 prob = cvx.Problem(obj , constraint)# 問題
14 prob.solve(verbose=True) # 解く
15 # 表示
16 print("obj:␣", prob.value)
17 print("x:␣", x.value)
--------------------------------------------------------------
OSQP v0.6.0 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2019
--------------------------------------------------------------
problem: variables n = 2, constraints m = 3
nnz(P) + nnz(A) = 6
settings: linear system solver = qdldl,
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 10000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: on, time_limit: off
iter objective pri res dua res rho time
1 -7.4877e+00 1.19e+01 9.40e-01 1.00e-01 4.41e-05s
100 9.0731e-02 5.29e-06 8.86e-07 1.00e-01 1.59e-04s
plsh 9.0733e-02 4.21e-17 1.62e-16 -------- 2.39e-04s
status: solved
solution polish: successful
number of iterations: 100
optimal objective: 0.0907
run time: 2.39e-04s
optimal rho estimate: 2.06e-01
obj: 0.0907327725771105
x: [0.97672897 0.22864252]
出力結果
• @で行列の積 (Python3.5 以降の
numpy と同等)
• seed によっては解なしになります:
obj: -inf
x: None
9 / 27

例題: 最小二乗法（二次計画問題：QP）
min
x
∥Ax − b∥2
2
1 np.random.seed (1)
2 # 次元数
3 m = 10
4 n = 4
5 # 定数・変数
6 A = np.random.randn(m, n)
7 b = np.random.randn(m)
8 x = cvx.Variable(n)
9 # 問題定義
10 obj = cvx.Minimize(cvx. sum_squares(A @ x - b))
11 prob = cvx.Problem(obj)
12 prob.solve(verbose=True)
13 # 結果表示
15 print("x:␣", x.value)
--------------------------------------------------------------
--------------------------------------------------------------
nnz(P) + nnz(A) = 60
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
1 0.0000e+00 2.10e+00 4.19e+02 1.00e-01 6.67e-05s
50 6.8125e+00 2.75e-09 5.65e-09 1.00e-01 1.43e-04s
plsh 6.8125e+00 1.93e-16 6.28e-16 -------- 2.14e-04s
status: solved
run time: 2.14e-04s
obj: 6.8124764971164895
x: [-0.82230179 -0.07243268 -0.43209417 -0.56574752]
出力結果
• cvx.sum_squares(A @ x - b)
は
cvx.norm(A @ x - b, p=2)**2
とも書ける
10 / 27

例題: 正定値射影（半正定値計画問題：SDP）
min
X∈Rn×n
∥A − X∥2
F s.t. X ⪰ O
ただし、X は対称行列
• X ⪰ O ⇔ a⊤Xa ≥ 0, ∀a ⇔ λi ≥ 0
1 # 行列用意
2 n = 2
3 A = np.random.randn(n, n)
4 A = A + A.T
5 X = cvx.Variable ((n,n), symmetric=True)
6 # 問題定義
7 constraints = [X >> 0] # 半正定値制約
8 obj = cvx.Minimize(cvx.norm(A-X, "fro")**2)
9 prob = cvx.Problem(obj , constraints)
11 # 結果表示
13 print("X:␣")
14 print(X.value)
----------------------------------------------------------
SCS v2.0.2 - Splitting Conic Solver
(c) Brendan O’Donoghue, Stanford University, 2012-2017
----------------------------------------------------------
... 略...
----------------------------------------------------------
Iter | pri res | dua res | rel gap | pri obj | dua obj |
----------------------------------------------------------
0| 1.73e+01 1.24e+01 9.86e-01 -4.31e+01 2.97e+01
40| 1.07e-09 7.26e-10 4.98e-12 5.65e+00 5.65e+00
----------------------------------------------------------
... 略...
==========================================================
obj: 5.649762619291792
X:
[[ 3.34243714 -0.67728402]
[-0.67728402 0.13723927]]
x
0 1 2 3 4 5
z
2 10 1 2 3 4 5
y
4
2
0
2
4
Figure: 射影結果 X =
[
x y
y z
]
11 / 27

例題: LASSO
1 data_boston = sklearn.datasets. load_boston ()
2 X = data_boston .data
3 y = data_boston .target
4 (n,d) = X.shape
5 lam = 3000
6 # 変数定義
7 w = cvx.Variable(d)
8 b = cvx.Variable ()
9 # 問題定義
10 obj = 0
11 for i in range(n):
12 obj += (X[i]@w+b-y[i])**2
13 obj += lam * cvx.norm(w, p=1)
14 obj = cvx.Minimize(obj)
15 prob = cvx.Problem(obj)
17 # 結果表示
19 print("w:␣")
20 print(w.value)
21 print("b:␣", b.value)
min
w,b
i
(w⊤
xi + b − yi)2
+ λ∥w∥1
-----------------------------------------------------------------
-----------------------------------------------------------------
nnz(P) + nnz(A) = 7305
eps_abs = 1.0e-05, eps_rel = 1.0e-05,
1 -3.1200e+05 5.00e+01 3.14e+09 1.00e-01 9.02e-04s
125 2.0944e+04 2.36e-07 3.91e-03 1.58e+00 4.53e-03s
plsh 2.0944e+04 1.77e-14 4.53e-09 -------- 5.48e-03s
status: solved
run time: 5.48e-03s
obj: 20943.90569047654
w:
[-7.19968502e-22 3.70710298e-02 -1.25172384e-22 6.54692200e-23
5.85580644e-23 1.19903058e-21 4.26077027e-02 -6.03200815e-22
6.58077009e-02 -8.71847487e-03 -2.75870957e-01 6.53849409e-03
-8.08355572e-01]
b: 35.10791530160754
12 / 27

例題: SVM
1 # 適当にデータ作成
2 n = 100
3 X, y = make_classification ( random_state =8,
n_samples=n,n_features =2, n_redundant =0,
n_informative =2, n_clusters_per_class =1,
n_classes =2)
4 y[y == 0] = -1
5 C = 1
6 # 変数
7 w = cvx.Variable (2)
8 b = cvx.Variable ()
9 xi = cvx.Variable(n)
10 # 問題定義
11 obj = cvx.Minimize( cvx.sum_squares (w) / 2 +
C * cvx.sum(xi) )
12 constraint = [xi >= 0] + [(xi[i] >= 1 - y[i
]*( w@X[i]+b)) for i in range(n)]
13 prob = cvx.Problem(obj , constraint)
min
w,b,ξ
1
2
∥w∥2
2 + C
i
ξi
s.t. ξi ≥ 1 − yi(w⊤
xi + b),
ξi ≥ 0
1.5 1.0 0.5 0.0 0.5 1.0 1.5 2.0
3
2
1
0
1
2
Figure: 最適化結果
13 / 27

注意点
• “@” だけでなく “*” も行列の積として扱われる（要素ごとの積ではない）
▶ 特にベクトル同士では内積になる
• 要素ごとの積は cvx.multiply を使う 1
SVM の例
• ξi ≥ 1 − yi(w⊤xi + b)
OK constraint = [(xi[i] >= 1 - y[i]*(w@X[i]+b)) for i in range(n)]
• ξ ≥ 1 − y ◦ (Xw + b) （◦: 要素ごとの積）
OK constraint = [xi >= 1 - cvx.multiply(y, X@w+b)]
NG constraint = [xi >= 1 - y*(X@w+b)]
1
https://www.cvxpy.org/tutorial/functions/index.html?highlight=elementwise
14 / 27

目次
4 まとめ
15 / 27

双対問題
• 主問題（オリジナル）を変形して双対問題を作ることができる
• 凸最適化では（大抵の場合 2）主問題と双対問題の最適値が一致する
▶ 解きやすい方を解けば良い
▶ 双対のほうがよい例: SVM
min
w
n
i=1
max{0, 1 − yiw⊤
xi} +
λ
2
∥w∥2
2 (Primal)
max
α∈[0,1]n
−
1
2λ
α⊤
Qα + 1⊤
α (Dual)
ただし、Qij := yiyjx⊤
i xj
⋆ 双対問題は二次形式になる
• 双対ギャップ（= 主問題の値 − 双対問題の値）が 0 なら最適解
▶ 最適化アルゴリズムの停止条件として使える
2
のちに詳しく説明
16 / 27

ラグランジアン
Convex Optimization (Boyd) の 5 章 Duality に対応
Qiita により詳しくまとめてあります https://qiita.com/birdwatcher/items/b23209f06177373c6df4
次の最小化問題を考える（主問題）:
min
x∈Rn
f0(x)
s.t. fi(x) ≤ 0, i = 1, . . . , m
hi(x) = 0, i = 1, . . . , p
• 実行可能領域は空でないとする
• この最適化問題の最適値を p⋆ と書く
• 凸性は特に仮定しない
ラグランジアンの定義:
L(x, λ, ν) := f0(x) +
m
i=1
λifi(x) +
p
i=1
νihi(x)
• λi, νi: ラグランジュ未定乗数
17 / 27

ラグランジュ双対関数
定義:
g(λ, ν) := inf
x∈D
L(x, λ, ν)
= inf
x∈D
f0(x) +
m
i=1
λifi(x) +
p
i=1
νihi(x)
• D := m
i=0 dom(fi) ∩ p
i=1 dom(hi)
• 双対関数は必ず concave（上に凸）となる（もとの問題が凸でなくても）
▶ (λ, ν) のアフィン関数の各点での inf になっているため 3
3
Qiita に証明を載せてます
18 / 27

最適値の下限: 双対関数の値は主問題の最適値を超えない
任意の λ ≥ 0, ν に対して次が成り立つ
g(λ, ν) ≤ p⋆
証明：
• ˜x を実行可能解とする: fi(˜x) ≤ 0, hi(˜x) = 0
• L(˜x, λ, ν) の値は f0(˜x) でおさえられる：
L(˜x, λ, ν) = f0(˜x) +
m
i=1
λifi(˜x)
≤0
+
p
i=1
νihi(˜x)
=0
≤ f0(˜x)
• ゆえに g(λ, ν) は f0(˜x) でおさえられる
∴ g(λ, ν) = inf
x∈D
L(x, λ, ν) ≤ L(˜x, λ, ν) ≤ f0(˜x)
• 任意の ˜x に対して, g(λ, ν) ≤ f0(˜x) が成り立つため、g(λ, ν) ≤ p⋆ が成り立つ
19 / 27

ラグランジュ双対問題
• ここまでで双対関数が主問題の下限を与えるとわかった
• 自然な疑問：ラグランジュ双対関数から得られる最も良い下限は？
最も良い下限は次の最大化問題を解くことで得られる：
max
λ,ν
g(λ, ν)
s.t. λ ≥ 0
• ラグランジュ双対問題と呼ばれる
• 双対実行可能領域: (λ, ν) に対して λ ≥ 0, g(λ, ν) > −∞
• (λ⋆, ν⋆): 双対問題の最適解
• d⋆: 双対問題の最適値
• 双対問題は必ず凸最適化問題
▶ 目的関数が必ず concave で, 制約が凸であるため
▶ 主問題が凸最適化でなくても成り立つ
20 / 27

弱双対性
d⋆
≤ p⋆
• 主問題の凸性にかかわらず成り立つ
• この不等式は p⋆, d⋆ が発散しないときに成り立つ
• p⋆ − d⋆ を双対ギャップという
▶ 最適化アルゴリズムの停止条件によく使われる
• p⋆ を求めることが難しいときに d⋆ を求めることで、p⋆ の下限を知れる
▶ 双対問題は必ず凸であるため, 多くの場合効率的に解ける
21 / 27

強双対性
d⋆
= p⋆
• 主問題の最適値が双対問題の最適値と一致するという性質
• 強双対性は常には成り立たない
もし主問題が凸、すなわち:
min
x∈Rn
f0(x)
s.t. fi(x) ≤ 0, i = 1, . . . , m
Ax = b
で f0, . . . , fm が凸なら、たいていは (いつもではない) 強双対性が成り立つ
• 例：SVM の最適化問題は凸であり強双対性が成り立つため、主問題/双対問題の
どちらを解いてもよい
22 / 27

スレーター条件
次のような x ∈ relint(D) が存在することをいう
fi(x) < 0, i = 1, . . . , m, Ax = b
• 主問題が凸でスレーター条件を満たすとき、強双対性が成り立つ
• スレーター条件は強双対性の十分条件である (必要十分ではない)
もし、f1, . . . , fk がアフィンなら、より弱い条件が成り立てばよい:
fi(x) ≤ 0, i = 1, . . . , k, fi(x) < 0, i = k + 1, . . . , m, Ax = b
• 言い換えれば, アフィンの不等式制約は等号を含んでもよい
23 / 27

最適性条件: 相補性条件
強双対性を満たすと仮定すると、
f0(x⋆
) = g(λ⋆
, ν⋆
) (∵ 強双対性)
= inf
x∈D
f0(x) +
m
i=1
λ⋆
i fi(x) +
p
i=1
ν⋆
i hi(x) (∵ 双対関数の定義)
≤ f0(x⋆
) +
m
i=1
λ⋆
i fi(x⋆
) +
p
i=1
ν⋆
i hi(x⋆
) (∵ inf の定義)
≤ f0(x⋆
) (∵ λ⋆
i ≥ 0, fi(x⋆
) ≤ 0, i = 1, . . . , m と hi(x⋆
) = 0, i = 1, . . . , p)
1,3 行目と 3,4 行目を考慮すると、 m
i=1 λ⋆
i fi(x⋆) = 0. 和の各項は同符号であるため,
λ⋆
i fi(x⋆
) = 0, i = 1, . . . , m.
これを相補性条件という
• もし λ⋆
i > 0 なら, fi(x⋆) = 0
• もし fi(x⋆) < 0 なら, λ⋆
i = 0
24 / 27

最適性条件: KKT 条件（Karush-Kuhn-Tucker 条件）
強双対性を仮定すると, x⋆ は L(x, λ⋆, ν⋆) を最小化するため, x⋆ における勾配は 0:
∇f0(x⋆
) +
m
i=1
λ⋆
i ∇fi(x⋆
) +
p
i=1
ν⋆
i ∇hi(x⋆
) = 0
最適解で成り立つ式を列挙すると：
• fi(x⋆) ≤ 0, i = 1, . . . , m （制約）
• hi(x⋆) = 0, i = 1, . . . , p （制約）
• λi ≥ 0, i = 1, . . . , m （双対変数の制約）
• λifi(x⋆) = 0, i = 1, . . . , m （相補性条件）
• ∇f0(x⋆) + m
i=1 λ⋆
i ∇fi(x⋆) + p
i=1 ν⋆
i ∇hi(x⋆) = 0 （勾配が 0）
これが KKT 条件である（必要条件。主問題が凸なら KKT 条件は十分条件にもなる）
• 強双対性を満たすなら, 最適解において KKT 条件を満たさなければならない
• 主問題が凸でスレーター条件を満たすとき、KKT 条件は最適性の必要十分条件
25 / 27

目次
4 まとめ
26 / 27

まとめ
• CVXPY は式の見た目通りに書ける
• Convex Optimization はわかりやすい
▶ 幾何的な解釈や鞍点解釈などの説明も載っているので興味のある方は読むよい
• 双対問題は、主問題の下限を最もよくおさえるための問題である
• 凸最適化問題なら大抵の場合、主問題の最適値 = 双対問題の最適値
• スレーター条件を満たすとき、KKT 条件は最適性の必要十分条件となる
• その他、線形近似解釈、フェンシェル双対との関係、凸共役などは Qiita へ
▶ https://qiita.com/birdwatcher/items/b23209f06177373c6df4
27 / 27

凸最適化 〜 双対定理とソルバーCVXPYの紹介 〜

More Related Content