Euclids geometry for class IX by G R Ahmed
- 3. The word geometry is derived from the Greek word “Geo” means the earth and “metron” means measurement. Thus the word geometry means the measurment of earth. Ancient Egyptians were the first people to study geometry. They were mainly concerned with problems of finding the areas of plane figures such as triangles, rectangles etc. Later Babylonians discovered formulae for finding areas of various rectilinear figures. He introduced the method of proving mathematical results by using logical reasoning and the previously proved result. The Geometry of plane figure is know as "Euclidean Geometry".
- 4. Axioms or Postulates- • are basic facts which are obvious and universal truths and need no proof. Theorems- • are statements which are proved , using definitions, axioms, previously proved statements and deducting reasoning.
- 5. Statements : A sentence which is either true or false but not both, is called a statement. eg. (i) 4+9=6 If is a false sentence, so it is a statement. (ii) Sajnay is tall. This is not a statement because he may be tall for certain persons and may not be taller for others. Theorems : A statement that requires a proof is called a theorem. eg. (i) The sum of the angles of triangle is 1800. (ii) The angles opposite to equal sides of a triangles are equal. Corollary - Result deduced from a theorem is called its corollary.
- 6. Some undefined term There are three basic concepts in geometry namely, point, line and plane. It is not possible to define these three concepts precisely. We can have a good idea of these concepts by considering examples as given below. Point: A point is represented by a fine dot made by a sharp pencil on a sheet of paper. Plane: The surface of a smooth wall, or the surface of a sheet of paper or the surface of a smooth black board are close example of a plane.Geometrical plane extend endlessly in all dirrections. Line:If we fold a paper the crease in the paper represents a geometrical straight line. A geometrical straight line is collection of points and extends endlessly in both dirrections.
- 7. some Euclid's axioms are (i) Things which are equal to the same thing are equal to one another. i.e. If a=b and b=c then a=c (ii) If equals are added to equals, the wholes are equal i.e. If a=b then a+c=b+c (iii) If equals are subtracted from equals, the remainders are equal i.e. If a=b then a-c=b-c (iv) Things which coincide with one another are equal to one another. (v) The whole is greater than the part.
- 8. Incidence Axioms: Axiom1: A line contains infinitely many points. Axiom2: Through a given points there pass infinitely many lines. Axiom3: Given two points A and B ,there is only one line that contains both the points. It follows from third axiom that a line is completely known if we know the positions of two distinct points on it. For this reasons a line with two distinct points A and B on it is
- 9. Postulate 1 1. A straight line may be drawn from any point to any other point. A B
- 10. Postulate 2 • Any line segment can be extended indefinitely to form a line C D Given line segment CD, you can extend it to make line CD
- 11. Postulate 3 • Given a line segment, a circle can be drawn having the segment as a radius and one endpoint as a center
- 12. Postulate 4 •All right angles are congruent G F E GFE
- 14. If l is any line and P is any point not on l, then there exists exactly one line m through P that is parallel to l.
- 15. In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid (the parallel postulate): In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point. It is equivalent to Euclid's parallel postulate in the context of Euclidean geometry and was named after the Scottish mathematician John Playfair.
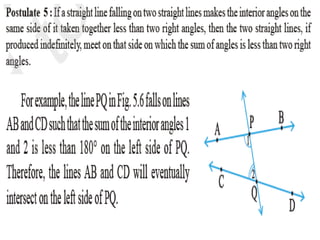
- 16. Limit of postulate 5 •Postulate 5 is only true in a _______ and cannot be applied to a_________ plane curve
- 17. A set of axioms are called consistent if it is impossible to derive a contradiction from the Axiom. So when any system of axioms is given, it needs to be ensured that the system is consistent.
- 18. The Axioms of Incidence The following axioms set out the basic incidence relations between lines, points and planes. Incidence between points and lines: There are at least two distinct points. There is one and only one line that contains two distinct points. Every line contains at least two distinct points. Incidence between points and planes: There are three points that do not all lie on the same line. For any three points that do not lie on the same line there is a one and only one plane that contains them. Any plane contains at least three points.
- 19. Conjecture:A conjecture is a hypothesis that appears to be true but has not yet been proved to be true. “Every even number is the sum of two primes”. For example 2 = 1 +1 12 = 7 + 5 4 = 2 + 2 14 = 7 + 7 6 = 3 + 3 16 = 13 + 3 8 = 5 + 3 18 = 13 + 5 10 = 5 + 5 20 = 17 + 3
- 20. Gold Bach's conjecture “Every even number is the sum of two primes”. This has been tested on computers up to the number 100,000,000,000,000 and has been found true for all these numbers. But it has not yet been proved true for ALL numbers, hence it is a conjecture.
- 21. Euclid's 23 definitions Definition 1. A point is that which has no part. Definition 2. A line is breathless length. Definition 3. The ends of a line are points. Definition 4. A straight line is a line which lies evenly with the points on itself. Definition 5. A surface is that which has length and breadth only. Definition 6. The edges of a surface are lines. Definition 7. A plane surface is a surface which lies evenly with the straight lines on itself.
- 22. Definition 8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line. Definition 9. And when the lines containing the angle are straight, the angle is called rectilinear. Definition 10. When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. Definition 11. An obtuse angle is an angle greater than a right angle. Definition 12. An acute angle is an angle less than a right angle. Definition 13. A boundary is that which is an extremity of anything.
- 23. Definition 14. A figure is that which is contained by any boundary or boundaries. Definition 15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another. Definition 16. And the point is called the center of the circle. Definition 17. A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle. Definition 18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center of the semicircle is the same as that of the circle. Definition 19. Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
- 24. Definition 20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal. Definition 21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute. Definition 22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia. Definition 23 Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.