Full document (1)

TABLE OF CONTENTS
List of Figures ..........................................................................................................................................2
Indices.....................................................................................................................................................3
First Law:.............................................................................................................................................3
Second Law: ........................................................................................................................................3
Third Law:............................................................................................................................................3
Fourth Law: .........................................................................................................................................4
Fifth Law:.............................................................................................................................................4
Fractional Indices:...............................................................................................................................4
Examples:............................................................................................................................................5
Logarithm................................................................................................................................................6
Relation between indices and logarithm............................................................................................7
Logarithm rules...................................................................................................................................7
Examples:............................................................................................................................................7
Multiplication using logarithm..........................................................................................................11
Division using logarithm....................................................................................................................11
Calculation of Power using Logarithm ..............................................................................................12
Calculation of Root using Logarithm.................................................................................................12
Anti-Logarithms.....................................................................................................................................13
Examples:..........................................................................................................................................15
Quiz ...................................................................................................................................................16

LIST OF FIGURES
Figure 1...................................................................................................................................................9
Figure 2.................................................................................................................................................10
Figure 3.................................................................................................................................................10
Figure 4.................................................................................................................................................13
Figure 5.................................................................................................................................................14
Figure 6.................................................................................................................................................14

INDICES
The plural of index is known as indices, where an index is used to compactly write a product
or a number.
In the expression , the index or exponent or power is “a” and the number ” is called the
base. Laws of indices are used to manipulate the expressions with indices. There are total
four laws of indices, each one of them is explained one by one as follow;
First Law:
When expressions with the same base are multiplied, the indices of all the expressions are to
be added.
In general,
Let’s a = 4, b = 2 and x = 3;
Then
Second Law:
When expressions with the same base are divided, the index of the expression in the
denominator is subtracted from the index of the expression in the numerator.
In general,
Let’s a = 4, b = 2 and x = 3;
Then
Third Law:
When the index of the expression is 0 then the whole expression become equal to 1.
In general,
80
= 1

Fourth Law:
When the index of an expression is equal to a negative number, then the same expression
with a positive index is written in a fraction form, with numerator equal to 1 and denominator
equal to that specified expression. It can be explained with the following example;
In general,
Let’s a = 4 and x = 3;
Fifth Law:
When the power of the base is raised to another power then indices are to be multiplied.
In general, (am
)n
= amn
.
Here the power or index “m” of the base “a” is raised to the power “n”, thus both the power
are multiplied with each other.
Let’s m = 2, n = 2 and a = 3;
Fractional Indices:
Fractional indices are represented by a base number with a fractional index or power or
exponent. In general, a fractional index is in the form of . The index laws are also
applicable to the fractional indices, for example squaring the expression means
multiplying the index by 2.
The fractional index is also known as positive square root and is represented by the symbol
√. For example the square root of 4 is equal to 2. It can further be explained as follow;
√
In order to simplify the expression,

Thus
√
Similarly √ , and so on.
Examples:
Simplify
As ;
Thus
Simplify
First of all we will simplify the expression in parenthesis;
=
=
=
Simplify

Simplify √
√
Simplify
LOGARITHM
In the simplest way, Logarithm definition provides the answer of the following question.
“How many of one number do we multiply to get another number?”
For example: how many 4s do we multiply to get 64?
Answer: 4x4x4 = 64, so we needed to multiply 3 of the 4s to get 64.
Logarithm represents the above answer in the following format: log4 (64) = 3
The number we are multiplying is called the base. Thus we can rephrase our answer as, the
logarithm of 64 with base 4 is equal to 3 or the log base 4 of 64 is 3.
All Logarithms with the base 10 are known as common logarithms. There is no need to
mention the base.
For example: log 100 = 2

In other words, it can also be written as log10 100 = 2
Relation between indices and logarithm
As square root of a number is the inverse process to squaring a number; in the same way,
taking a logarithm is the inverse process to taking a power.
Considering previous example; log4(64) = 3 in exponential form can be written as 43
= 64.
4x4x4 = 43
= 64, the index of base 4 is 3, and it is equal to 64, while the same index 3 is the
answer of log base 4 of 64.
Logarithm rules
Total three rules of logarithm will be discussed here.
1. log (a*b) = log a + log b, where the base will remains the same on both sides of equation.
2. log (a/b) = log a - log b, where the base will remains the same on both sides of equation.
3. Log (ab
) = b*log a, where the base will remains the same on both sides of equation.
Examples:
Find the value of x;
log2 32 = x
In exponential form;
32 = 25
Thus
Log2 32 = 5, where x = 5
log2 x = 7
27
= 128
Thus
log2 128 = 7, where x = 128

logx 25 = 2
52
= 25
Thus
Log5 25= 2, where x = 5
Log x = 3
As the base is not mentioned, so it is understood to be a common logarithm, hence it can be
rewritten as;
Log10 x = 3
It can be transformed as 103
= x
103
= 100
Thus the value of x=100
If we want to calculate the value of log105, then it can be written in a form of 10x
= 5, where x
lies between 0 and 1. In order to calculate such problems, we either need a calculator or a
logarithmic table.
Log table is based on common logarithm. Before discussing the log table, lets first discus the
properties of logarithm, then we will move on to the log tables, because some of the
properties are required for solving questions based on log table.
Let's say we want to find the log base 10 of 15 on a common log table. 15 lies between 10
(101
) and 100 (102
), so its logarithm will lie between 1 and 2, or be 1.something. 150 lies
between 100 (102
) and 1000 (103
), so its logarithm will lie between 2 and 3, or be
2.something. The .something is called the mantissa. What comes before the decimal point (1
in the first example, 2 in the second) is known as characteristic. In figure 1, the leftmost
column will show the first two or, for some large log tables, three digits of the number whose
logarithm you're looking up.

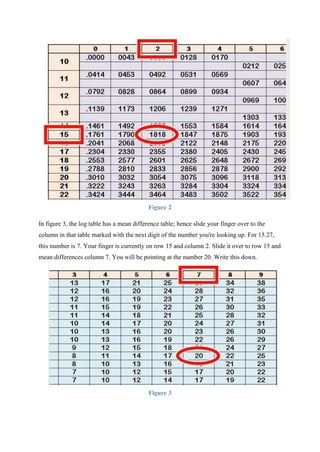
Figure 1
If you're looking up the log of 15.27 in a normal log table, go to the row marked 15 in figure
1. If you're looking up the log of 2.57, go to the row marked 25. Sometimes the numbers in
this row will have a decimal point, so you'll look up 2.5 rather than 25. You can ignore this
decimal point, as it won't affect your answer. Also ignore any decimal points in the number
whose logarithm you're looking up, as the mantissa for the log of 1.527 is no different from
that of the log of 152.7.
On the appropriate row, slide your finger over to the appropriate column. This column will be
the one marked with the next digit of the number whose logarithm you're looking up. For
example, in figure 2, if you want to find the log of 15.27, your finger will be on the row
marked 15. Slide your finger along that row to the right to find column 2. You will be
pointing at the number 1818. Write this down.

Figure 2
In figure 3, the log table has a mean difference table; hence slide your finger over to the
column in that table marked with the next digit of the number you're looking up. For 15.27,
this number is 7. Your finger is currently on row 15 and column 2. Slide it over to row 15 and
mean differences column 7. You will be pointing at the number 20. Write this down.
Figure 3

Add the numbers found in the two preceding steps together. For 15.27, you will get 1838.
This is the mantissa of the logarithm of 15.27.
1818 + 20 = 1838
Since 15 is between 10 and 100 (101
and 102
), the log of 15 must be between 1 and 2, so
1.something, hence the characteristic is 1. Combine the characteristic with the mantissa to get
your final answer. Finally the log of 15.27 is 1.1838.
Multiplication using logarithm
The sum of the logarithms of two different numbers is the logarithm of the product of those
numbers. In general,
For example, if you want to multiply 15.27 and 48.54, you would find the log of 15.27 to be
1.1838 and the log of 48.54 to be 1.6861.
In this example, add 1.1838 and 1.6861 to get 2.8699. This number is the logarithm of your
answer.
You can do this by finding the number in the body of the table closest to the mantissa of this
number (8699). The more efficient and reliable method, however, is to find the answer in the
table of anti-logarithms, as described in the method above. For this example, you will get
741.1.
Division using logarithm
The difference of the logarithms of two different numbers is the logarithm of the division of
those numbers. In general,
For example, if you want to divide 15.27 over 48.54, you would find the log of 15.27 to be
1.1838 and the log of 48.54 to be 1.6861.
In this example, subtract 1.1838 from 1.6861 to get 0.5023. This number is the logarithm of
your answer.
The more efficient and reliable method, however, is to find the answer in the table of anti-
logarithms, as described in the method above. For this example, you will get 3.179.

Calculation of Power using Logarithm
In general, log (a) = n or 10n
= a; In order to calculate the answer of 21.532
, first we take the
log of the number without its exponent or power using log table;
log ( 21.53) = 1.333
Now in exponential form, the expression becomes;
101.333
= 21.53
Squaring both sides of the equation;
(101.333
)2
= 21.532
Using the indices property; (ax
)y
= ax*y
Thus
102.666
= 21.532
Now the anti-log of 2.666 will give us the final answer of 21.532
, which is 463.44.
Calculation of Root using Logarithm
The same method of calculating power using logarithm is applicable to root calculation. A
simple root (√) is equal to power 1/2, while ( is equal to power 1/3 and so on.
Let’s have an example of using logarithm to calculate the value of 850.
First of all convert 850 into exponential form as;
850 = 8501/4
Now calculate the logarithm of 850 using log table;
log (850) = 2.9294
In exponential form, log (850) = 2.9294 can be written as 102.9294
= 850
Thus
850 = 8501/4
= (102.9294
)1/4
=102.9294
*1/4
= 100.73235
Finally the anti-log of 0.73235 is 5.3994, which is the final answer of 850.

ANTI-LOGARITHMS
Use Anti-log table, when you have the log of a number but not the number itself. In the
formula 10n
= x, n is the common log, or base-ten log, of x. If you have x, find n using the log
table. If you have n, find x using the anti-log table.
Characteristic is the number before the decimal point. If you're looking up the anti-log of
2.8699, the characteristic is 2. Mentally remove it from the number you're looking up, but
make sure to write it down so you don't forget it.
Find the row that matches the first part of the mantissa. In 2.8699, the mantissa is .8699. Most
anti-log tables, like most log tables, have two digits in the leftmost column as shown in figure
4, so run your finger down that column until you find .86.
Figure 4
Slide your finger over to the column marked with the next digit of the mantissa. For 2.8699,
slide your finger along the row marked .86 to find the intersection with column 9. This is
shown as 7396 in figure 5. Write this down.

Figure 5
The anti-log table shown in figure 6 has a table of mean differences; thus slide your finger
over to the column in that table marked with the next digit of the mantissa. Make sure to keep
your finger in the same row.
Figure 6

In this case, you will slide your finger over to the last column in the table, column 9. The
intersection of row .86 and mean differences column 9 is 15. Write that down.
Add the two numbers from the two previous steps. In our example, these are 7396 and 15.
Add them together to get 7411.
Use the characteristic to place the decimal point. Our characteristic was 2. This means that
the answer is between 102
and 103
, or between 100 and 1000. In order for the number 7411 to
fall between 100 and 1000, the decimal point must go after three digits, so that the number is
about 700 rather than 70, which is too small, or 7000, which is too big. So the final answer is
741.1.
Thus the anti-log of 2.8699 is 741.1, i.e.
Anti-log (2.8699) = 741.1
Or
102.8699
= 741.1
Examples:
Calculate the anti-log of 2.80.
The characteristic here is 2, while the mantissa is 80. The .80 comes across 6310 under column 0. Use
the characteristic to place the decimal point. Our characteristic was 2. This means that the
answer is between 102
and 103
, or between 100 and 1000. In order for the number 6310 to fall
between 100 and 1000, the decimal point must go after three digits, thus the final answer is
631.0.
The characteristic here is 1, while the mantissa is 943. The .94 comes across 8770 under column 3.
Use the characteristic to place the decimal point. Our characteristic was 1. This means that
the answer is between 101
and 102
, or between 10 and 100. In order for the number 8770 to
fall between 10 and 100, the decimal point must go after two digits, thus the final answer is
87.70.

For an anti-log table with another table of mean differences, the value that comes across the mantissa
fourth digit 4 in the same row of .92 is 8. Now addition of 8395 and 8 gives 8403. Use the
characteristic to place the decimal point. Our characteristic was 0. This means that the answer
is between 100
and 101
, or between 1 and 10. In order for the number 8403 to fall between 1
and 10, the decimal point must go after one digit, thus the final answer is 8.403.
is between 101
and 102
, or between 10 and 100. In order for the number 6879 to fall between
10 and 100, the decimal point must go after two digits, thus the final answer is 68.79.
is between 103
and 104
, or between 1000 and 10000. In order for the number 7741 to fall
between 1000 and 10000, the decimal point must go after four digits, thus the final answer is
7741.
Quiz
1. find the value of x;
√
(a) 8 (b) 4 (c) 2 (d) 16 (e) 32
2. √ √
(a) 14 (b) 12 (c) 10 (d) 16 (e) 20

3. The simplified form of
(a) (b) (c) (d) (e)
4. Which of the following represents
(a) (b) √ (c) √ (d) √ (e) √
5. Which of the following is the correct value of x in ?
(a) 50 (b) 100 (c) 10 (d) 1000 (e) 500
6. Using the log table, what is the value of 5.30?
(a) 0.7250 (b) 0.7242 (c) 0.7240 (d) 0.7252 (e) 0.7245
7. Solve for correct value of x.
(a) 15/2 (b) 15 (c) 2 (d) 2/15 (e) 3/15
8. Using anti-log table, which of the following is the correct value of 1.59333?
(a) 39 (b) 39.2 (c) 3.9 (d) 3.92 (e) 3.0
(a) 1.62 (b) 1.72 (c) 1.82 (d) 1.92 (e) 2.02
(a) 1.3268 (b) 1.3286 (c) 1.32 (d) 1.86 (e) 1.8632

Full document (1)

More Related Content

Full document (1)