Heuristics-biases.ppt
- 1. Heuristics and Biases Thomas R. Stewart, Ph.D. Center for Policy Research Rockefeller College of Public Affairs and Policy University at Albany State University of New York T.STEWART@ALBANY.EDU Public Administration and Policy PAD634 Judgment and Decision Making Behavior Copyright © Thomas R. Stewart
- 2. PAD634 (heuristics-biases.ppt) 2 Why study heuristics and biases? There are three related reasons for the focus on systematic error and inferential biases in the study of reasoning. First, they expose some of our intellectual limitations and suggest ways to improve the quality of our thinking. Second, errors and biases often reveal the psychological processes that govern judgment and inference. Third, mistakes and fallacies help the mapping of human intuitions by indicating which principles of statistics or logic are non-intuitive or counter-intuitive. (Tversky and Kahneman, 1982)
- 3. PAD634 (heuristics-biases.ppt) 3 Popular press discovers heuristics and biases (regularly) Newsweek, August 17, 1987
- 6. PAD634 (heuristics-biases.ppt) 6 Example: Framing (choice 1) Imagine that the U.S. is preparing for the outbreak of an unusual disease which is expected to kill 600 people. You have a choice between two programs: Program A: 200 people will be saved. Program B: either no one is saved (p=.67) or everyone is saved (p=.33)
- 7. PAD634 (heuristics-biases.ppt) 7 Example: Framing (choice 2) Imagine that the U.S. is preparing for the outbreak of an unusual disease which is expected to kill 600 people. You have a choice between two programs: Program A: 400 people will die Program B: either everyone dies (p=.67) or no one dies (p=.33)
- 8. PAD634 (heuristics-biases.ppt) 8 Example: Framing Choice 1-- Program A: 200 people will be saved. Program B: either no one is saved (p=.67) or everyone is saved (p=.33) Choice 2-- Program A: 400 people will die Program B: either everyone dies (p=.67) or no one dies (p=.33) 72% chose Program A 78% chose Program B
- 9. PAD634 (heuristics-biases.ppt) 9 The choices are formally the same Imagine that the U.S. is preparing for the outbreak of an unusual disease which is expected to kill 600 people. You have a choice between two programs: Choice 1-- Choice 2-- A: 200 people saved A: 400 people die B: no one saved (p=.67) B: everyone dies (p=.67) everyone saved (p=.33) no one dies (p=.33) Expected value of all programs = 200 lives saved
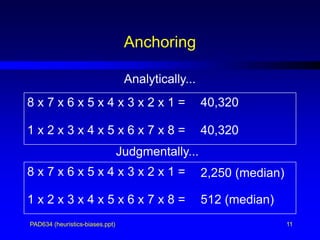
- 11. PAD634 (heuristics-biases.ppt) 11 Anchoring 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40,320 40,320 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = Analytically... Judgmentally... 2,250 (median) 512 (median)
- 13. PAD634 (heuristics-biases.ppt) 13 Example of availability Are there more words with r as the first letter or as the third letter? Most people say the first letter, but there are many more words with r as the third letter.
- 14. PAD634 (heuristics-biases.ppt) 14 Conjunction fallacy Linda is 31 years old, single, outspoken and very bright. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in antinuclear demonstrations. Which is more likely: 1. Linda is a bank teller. or 2. Linda is a bank teller and is active in the feminist movement. 85% of 142 college undergraduates said statement 2 was more likely than statement 1.
- 15. PAD634 (heuristics-biases.ppt) 15 Conjunction fallacy By the multiplication rule, the joint probability (conjunction) of two events cannot exceed the probability of either event.
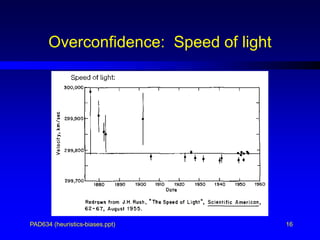
- 16. PAD634 (heuristics-biases.ppt) 16 Overconfidence: Speed of light
- 17. PAD634 (heuristics-biases.ppt) 17 Overconfidence: Rest mass of electron
- 18. PAD634 (heuristics-biases.ppt) 18 Wason four-card task • Are scientists and others subject to a “confirmation bias?” • Slides on Wason four-card task
- 19. PAD634 (heuristics-biases.ppt) 19 “Psychology of Judgment and Decision Making” The most popular book on judgment and decision making covers only coherence. Plous, S. (1993). The Psychology of Judgment and Decision Making. New York: McGraw-Hill.
- 20. PAD634 (heuristics-biases.ppt) 20 Prospect theory and sunk costs
- 21. PAD634 (heuristics-biases.ppt) 21 Critiques of heuristics and biases • Gigerenzer • Lopes • Hogarth
- 22. PAD634 (heuristics-biases.ppt) 22 Gerd Gigerenzer: People are frequentists Gigerenzer, G. (1991). How to make cognitive illusions disappear: Beyond "heuristics and biases. European Review of Social Psychology, 2, 84-115. Gigerenzer’s critique
- 23. PAD634 (heuristics-biases.ppt) 23 Conjunction fallacy revisited Linda is 31 years old, single, outspoken and very bright. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in antinuclear demonstrations. Which is more likely: 1. Linda is a bank teller. or 2. Linda is a bank teller and is active in the feminist movement. 85% of 142 college undergraduates said statement 2 was more likely than statement 1. Gigerenzer’s critique
- 24. PAD634 (heuristics-biases.ppt) 24 Conjunction fallacy revisited Linda is 31 years old, single, outspoken and very bright. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in antinuclear demonstrations. There are 100 persons who fit the description above. How many of them are (a) bank tellers (b) bank tellers and active in the feminist movement. 22% of 44 subjects said statement b was more likely than a. Gigerenzer’s critique
- 25. PAD634 (heuristics-biases.ppt) 25 Base rate fallacy If a test to detect a disease whose prevalence is 1/1000 has a false positive rate of 5%, what is the chance that a person found to have a positive result actually has the disease, assuming you know nothing about the person’s symptoms or signs? – 60 students and staff at Harvard Medical school – Almost half judged the probability to be .95 – Only 18% responded .02 (the correct answer). (Note that true positive rate was not given.) Gigerenzer’s critique Bayesian belief updating
- 26. PAD634 (heuristics-biases.ppt) 26 Base rate fallacy revisited One out of 1000 Americans has disease X. A test has been developed to detect when a person has disease X. Every time the test is given to a person who has the disease, the test comes out positive. But sometimes the test also comes out positive when it it given to a person who is completely healthy. Specifically, out of every 1000 people who are perfectly healthy, 50 of them test positive for the disease. Imagine that we have assembled a random sample of 1000 Americans. They were selected by lottery. Those who conducted the lottery had no information about the health status of any of these people. How many people who test positive for the disease will actually have the disease? ______ out of _______ Gigerenzer’s critique
- 27. PAD634 (heuristics-biases.ppt) 27 Base rate fallacy revisited One out of 1000 Americans has disease X. A test has been developed to detect when a person has disease X. Every time the test is given to a person who has the disease, the test comes out positive. But sometimes the test also comes out positive when it it given to a person who is completely healthy. Specifically, out of every 1000 people who are perfectly healthy, 50 of them test positive for the disease. Imagine that we have assembled a random sample of 1000 Americans. They were selected by lottery. Those who conducted the lottery had no information about the health status of any of these people. How many people who test positive for the disease will actually have the disease? ______ out of _______ The Bayesian answer of .02 (one out of 50, or 51) was given by 76% of 50 subjects. Gigerenzer’s critique
- 28. PAD634 (heuristics-biases.ppt) 28 Lola Lopes: Results are oversold By constructing experiments so that normative theory makes one prediction and heuristics another, non- representative designs are created. Lopes, L. L. (1991). The rhetoric of rationality. Theory & Psychology, 1, 65-82. Lopes’ critique
- 29. PAD634 (heuristics-biases.ppt) 29 Lola Lopes: Results are oversold Availability demonstration: Are there more words with r as the first letter or as the third letter? Most people say the first letter, but there are many more words with r as the third letter. But, there are 20 consonants. 12 are more common in the first position. 8 are more common in the third position. Availability gives the right answer more often than not! Lopes’ critique
- 30. PAD634 (heuristics-biases.ppt) 30 Lola Lopes: Results are oversold “We can conclude that people use heuristics rather than probability theory, but we cannot conclude that their judgments are generally poor.” (p. 75) Lopes’ critique
- 31. PAD634 (heuristics-biases.ppt) 31 Robin Hogarth: Beyond discrete biases I. To dismiss the literature because external validity has not been demonstrated would be naive. II. The more serious criticism is the failure to specify the conditions under which people do or do not perform well. III. This paper focuses on the continuous, dynamic nature of the judgment task. Hogarth’s critique Hogarth, R.M. (1981). Beyond discrete biases: Functional and dysfunctional aspects of judgmental heuristics. Psychological Bulletin, 90, 197-217.
- 32. PAD634 (heuristics-biases.ppt) 32 Robin Hogarth: Beyond discrete biases IV. Importance of feedback A. Judgment facilitates action which produces feedback. 1. e.g., motor activities such as driving a car 2. social interaction B. Discrete judgment studies often use tasks that are degraded by the absence of feedback and redundancy. Hogarth’s critique
- 33. PAD634 (heuristics-biases.ppt) 33 Robin Hogarth: Beyond discrete biases V. Judgmental accuracy: Analogy of aiming at a target 1. Highlights two critical dimensions of achievement a) Degree of commitment b) Availability and interpretation of feedback are often more important than predictive ability 2. Prescription - Avoid or reduce commitment and make good use of feedback (“keep your options open”). VI. He goes on to argue that heuristics may work well in dynamic situations. Hogarth’s critique
- 34. PAD634 (heuristics-biases.ppt) 34 Bottom line • Coherence matters, and it cannot be taken for granted. • Other than that, heuristics and biases research has produced no generalizations or theory, and probably never will. • For improving judgment and decision making, that doesn’t matter. • For guiding research on judgment and decision making, it does matter.
- 35. PAD634 (heuristics-biases.ppt) 35 Improving coherence of judgment and decision making processes • Experts should enforce coherence: – Decide what form of coherence matters • Logical coherence • Probability theory • Other – Learn how to do it and design an environment to facilitate coherence
- 36. PAD634 (heuristics-biases.ppt) 36 Improving coherence of judgment and decision making processes • Laypeople – Training and changing their environment may be difficult – Present information in a way that encourages coherence. – For example, Gigerenzer’s work suggest that weather forecasts should be given as frequencies rather than probabilities.