Integration (area)
- 1. Pengamiran (Luas) y = 4x 2 x y 0 4 Cari luas rantau berlorek
- 2. Pengamiran (Luas) y = 4x 2 x y 0 4 Luas rantau berlorek Cari luas rantau berlorek
- 3. Pengamiran (Luas) y 2 = 3x x y 0 y = 4 y = 2 Cari luas rantau berlorek
- 4. Pengamiran (Luas) y 2 = 3x x y 0 Luas rantau berlorek y = 4 y = 2 Cari luas rantau berlorek
- 5. Pengamiran (Luas) y = 5x – x 2 x y 0 5 P(3,6) y = 2x Q(5,0) Cari luas rantau berlorek 3 4 B ialah luas di bawah lengkung B y = 5x – x 2 x y 0 y = 2x P(3,6) Q(5,0) A A ialah luas di bawah garis lurus
- 6. Pengamiran (Luas) y = 5x – x 2 x y 0 5 Luas A = luas segitiga = 1 / 2 x 3 x 6 = 9 unit 2 P(3,6) y = 2x Q(5,0) Cari luas rantau berlorek 3 4 B A Luas B Luas rantau berlorek = Luas A + Luas B = 9 + =
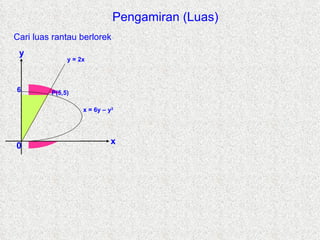
- 7. Pengamiran (Luas) Cari luas rantau berlorek y = 5x – x 2 x y 0 y = 2x A 6 P(5,5) x = 6y – y 2
- 8. Pengamiran (Luas) y = 5x – x 2 x y 0 y = 2x Cari luas rantau berlorek A 6 P(5,5) 5 Luas A = luas segitiga = 1 / 2 x 5 x 5 = 12.5 unit 2 x = 6y – y 2 A Luas rantau berlorek = Luas A + Luas B = 12.5 + = B Luas B
- 9. INTEGRATION -Pengamiran (Luas) y = – 3x 2 + 10x + 8 x y 0 y = 6x + 4 Cari koordinat bagi titik P dan Q . Seterusnya cari luas rantau berlorek P Q y = 6x + 4 …… ( 1 ) y = – 3x 2 + 10x + 8 …….. ( 2 ) Menentukan koordinat P dan Q. per (1) = per (2) 6x + 4 = – 3x 2 + 10x + 8 3x 2 - 10x - 8 + 6x + 4 = 0 3x 2 - 4x - 4 = 0 (3x + 2)(x – 2) = 0 x = -2 / 3 atau x = 2 Gantikan x = -2 / 3 ke dlm per (1) y = 6( -2 / 3 ) + 4 = 0 Gantikan x = 2 ke dlm per (1) y = 6(2 ) + 4 = 16 Koordinat P( -2 / 3 , 0) dan Q(2, 16)
- 10. Pengamiran (Luas) y = – 3x 2 + 10x + 8 x y 0 y = 6x + 4 Cari koordinat bagi titik P dan Q . Seterusnya cari luas rantau berlorek P Q
- 11. Pengamiran (Luas) Luas rantau berlorek Luas di bawah lengkung Luas di bawah garis lurus =28 unit 2 . =20 unit 2 . x y 0 P y = – 3x 2 + 10x + 8 Q 2 x y 0 y = 6x + 4 P Q x y 0 y = 6x + 4 P Q Luas Luas
- 12. Pengamiran (Luas) Luas rantau berlorek Luas di bawah lengkung Luas di bawah garis lurus =28 unit 2 . =20 unit 2 . = 8 unit 2. =28 - 20 Luas rantau berlorek x y 0 y = 6x + 4 P Q Luas Luas x y 0 P y = – 3x 2 + 10x + 8 Q 2 x y 0 y = 6x + 4 P Q
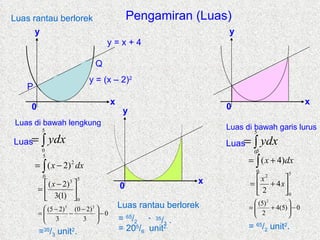
- 13. Cari koordinat bagi titik P dan Q . Seterusnya cari luas rantau berlorek y = x + 4 … … ( 1 ) y = (x - 2 ) 2 …….. ( 2 ) Menentukan koordinat P dan Q. per (1) = per (2) x + 4 = ( x – 2 ) 2 x 2 - 4x + 4 - x - 4 = 0 x 2 - 5x = 0 x(x – 5) = 0 x = 0 atau x = 5 Gantikan x =0 ke dlm per(1) y = 0 + 4 = 4 Gantikan x = 5 ke dlm per (1) y = 5 + 4 = 9 Koordinat P(0 , 4) dan Q(5, 9) Pengamiran (Luas) x y 0 y = (x – 2) 2 y = x + 4 P Q
- 14. Cari koordinat bagi titik P dan Q . Seterusnya cari luas rantau berlorek Pengamiran (Luas) x y 0 y = (x – 2) 2 y = x + 4 P Q
- 15. Luas di bawah lengkung Luas di bawah garis lurus = 35 / 3 unit 2 . = 65 / 2 unit 2 . y = (x – 2) 2 y = x + 4 Pengamiran (Luas) Luas rantau berlorek P Q x y 0 x y 0 x y 0 Luas Luas
- 16. Luas di bawah lengkung Luas di bawah garis lurus = 35 / 3 unit 2 . = 65 / 2 unit 2 . y = (x – 2) 2 y = x + 4 Pengamiran (Luas) Luas rantau berlorek Q Luas rantau berlorek P = 20 5 / 6 unit 2. = 65 / 2 - 35 / 3 . x y 0 x y 0 Luas Luas x y 0
- 17. Rajah di sebelah menunjukkan sebahagian daripada lengkung y 2 = 9 – x dan garis lurus 2x + 3y = 6. Hitungkan luas rantau berlorek x y y 2 = 9 - x 2x + 3y = 6 9 3 2 3
- 18. Luas rantau berlorek = Luas di bawah lengkung – luas segitiga - 6 - 6 x y y 2 = 9 - x 2x + 3y = 6 9 3 2 3