Lect4

Lecture outline Distance/Similarity between data objects Data objects as geometric data points Clustering problems and algorithms K-means K-median K-center

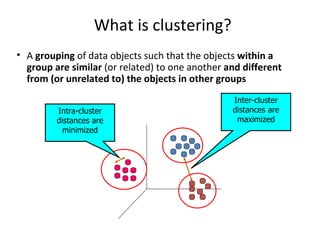
What is clustering? A grouping of data objects such that the objects within a group are similar (or related) to one another and different from (or unrelated to) the objects in other groups Inter-cluster distances are maximized Intra-cluster distances are minimized

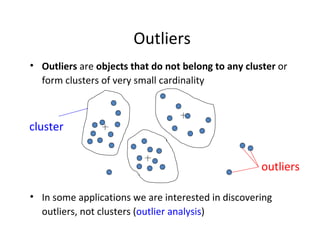
Outliers Outliers are objects that do not belong to any cluster or form clusters of very small cardinality In some applications we are interested in discovering outliers, not clusters ( outlier analysis ) cluster outliers

Why do we cluster? Clustering : given a collection of data objects group them so that Similar to one another within the same cluster Dissimilar to the objects in other clusters Clustering results are used: As a stand-alone tool to get insight into data distribution Visualization of clusters may unveil important information As a preprocessing step for other algorithms Efficient indexing or compression often relies on clustering

Applications of clustering? Image Processing cluster images based on their visual content Web Cluster groups of users based on their access patterns on webpages Cluster webpages based on their content Bioinformatics Cluster similar proteins together (similarity wrt chemical structure and/or functionality etc) Many more…

The clustering task Group observations into groups so that the observations belonging in the same group are similar, whereas observations in different groups are different Basic questions: What does “similar” mean What is a good partition of the objects? I.e., how is the quality of a solution measured How to find a good partition of the observations

Observations to cluster Real-value attributes/variables e.g., salary, height Binary attributes e.g., gender (M/F), has_cancer(T/F) Nominal (categorical) attributes e.g., religion (Christian, Muslim, Buddhist, Hindu, etc.) Ordinal/Ranked attributes e.g., military rank (soldier, sergeant, lutenant, captain, etc.) Variables of mixed types multiple attributes with various types

Observations to cluster Usually data objects consist of a set of attributes (also known as dimensions ) J. Smith, 20, 200K If all d dimensions are real-valued then we can visualize each data point as points in a d -dimensional space If all d dimensions are binary then we can think of each data point as a binary vector

Distance functions The distance d(x, y) between two objects x and y is a metric if d(i, j)  0 ( non-negativity ) d(i, i)=0 ( isolation ) d(i, j)= d(j, i) ( symmetry ) d(i, j) ≤ d(i, h)+d(h, j) ( triangular inequality ) [ Why do we need it? ] The definitions of distance functions are usually different for real , boolean , categorical, and ordinal variables. Weights may be associated with different variables based on applications and data semantics.

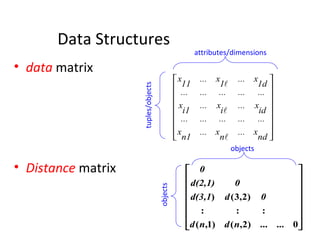
Data Structures data matrix Distance matrix attributes/dimensions tuples/objects objects objects

Distance functions for binary vectors Jaccard similarity between binary vectors X and Y Jaccard distance between binary vectors X and Y Jdist(X,Y) = 1- JSim(X,Y) Example: JSim = 1/6 Jdist = 5/6 Q1 Q2 Q3 Q4 Q5 Q6 X 1 0 0 1 1 1 Y 0 1 1 0 1 0

Distance functions for real-valued vectors L p norms or Minkowski distance : where p is a positive integer If p = 1, L 1 is the Manhattan (or city block) distance:

Distance functions for real-valued vectors If p = 2, L 2 is the Euclidean distance : Also one can use weighted distance : Very often L p p is used instead of L p (why?)

Partitioning algorithms: basic concept Construct a partition of a set of n objects into a set of k clusters Each object belongs to exactly one cluster The number of clusters k is given in advance

The k-means problem Given a set X of n points in a d -dimensional space and an integer k Task: choose a set of k points {c 1 , c 2 ,…,c k } in the d -dimensional space to form clusters {C 1 , C 2 ,…,C k } such that is minimized Some special cases: k = 1, k = n

Algorithmic properties of the k-means problem NP-hard if the dimensionality of the data is at least 2 ( d>=2 ) Finding the best solution in polynomial time is infeasible For d=1 the problem is solvable in polynomial time (how?) A simple iterative algorithm works quite well in practice

The k-means algorithm One way of solving the k -means problem Randomly pick k cluster centers {c 1 ,…,c k } For each i , set the cluster C i to be the set of points in X that are closer to c i than they are to c j for all i≠j For each i let c i be the center of cluster C i (mean of the vectors in C i ) Repeat until convergence

Properties of the k-means algorithm Finds a local optimum Converges often quickly (but not always) The choice of initial points can have large influence in the result

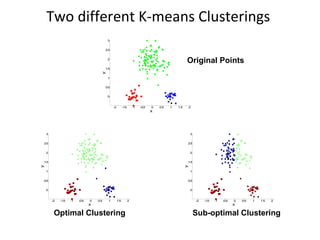
Two different K-means Clusterings Original Points Sub-optimal Clustering Optimal Clustering

Discussion k-means algorithm Finds a local optimum Converges often quickly (but not always) The choice of initial points can have large influence Clusters of different densities Clusters of different sizes Outliers can also cause a problem (Example?)

Some alternatives to random initialization of the central points Multiple runs Helps, but probability is not on your side Select original set of points by methods other than random . E.g., pick the most distant (from each other) points as cluster centers (kmeans++ algorithm)

The k-median problem Given a set X of n points in a d -dimensional space and an integer k Task: choose a set of k points {c 1 ,c 2 ,…,c k } from X and form clusters {C 1 ,C 2 ,…,C k } such that is minimized

The k - medoids algorithm Or … PAM (Partitioning Around Medoids, 1987) Choose randomly k medoids from the original dataset X Assign each of the n-k remaining points in X to their closest medoid iteratively replace one of the medoids by one of the non-medoids if it improves the total clustering cost

Discussion of PAM algorithm The algorithm is very similar to the k-means algorithm It has the same advantages and disadvantages How about efficiency?

CLARA (Clustering Large Applications) It draws multiple samples of the data set, applies PAM on each sample, and gives the best clustering as the output Strength : deals with larger data sets than PAM Weakness: Efficiency depends on the sample size A good clustering based on samples will not necessarily represent a good clustering of the whole data set if the sample is biased

The k-center problem Given a set X of n points in a d -dimensional space and an integer k Task: choose a set of k points from X as cluster centers {c 1 ,c 2 ,…,c k } such that for clusters {C 1 ,C 2 ,…,C k } is minimized

Algorithmic properties of the k-centers problem NP-hard if the dimensionality of the data is at least 2 (d>=2) Finding the best solution in polynomial time is infeasible For d=1 the problem is solvable in polynomial time (how?) A simple combinatorial algorithm works well in practice

The farthest-first traversal algorithm Pick any data point and label it as point 1 For i=2,3,…,n Find the unlabelled point furthest from {1,2,…,i-1} and label it as i . //Use d(x,S) = min y є S d(x,y) to identify the distance //of a point from a set π (i) = argmin j<i d(i,j) R i =d(i, π (i))

The farthest-first traversal is a 2-approximation algorithm Claim1 : R 1 ≥R 2 ≥… ≥R n Proof: R j =d(j, π (j)) = d(j,{1,2,…,j-1}) ≤ d(j,{1,2,…,i-1}) //j > i ≤ d(i,{1,2,…,i-1}) = R i

The farthest-first traversal is a 2-approximation algorithm Claim 2: If C is the clustering reported by the farthest algorithm, then R(C)=R k+1 Proof: For all i > k we have that d(i, {1,2,…,k})≤ d(k+1,{1,2,…,k}) = R k+1

The farthest-first traversal is a 2-approximation algorithm Theorem: If C is the clustering reported by the farthest algorithm, and C * is the optimal clustering, then then R(C)≤2xR(C * ) Proof: Let C* 1 , C* 2 ,…, C* k be the clusters of the optimal k-clustering. If these clusters contain points {1,…,k} then R(C)≤ 2R(C * ) (triangle inequality) Otherwise suppose that one of these clusters contains two or more of the points in {1,…,k} . These points are at distance at least R k from each other. Thus clusters must have radius ½ R k ≥ ½ R k+1 = ½ R(C)

What is the right number of clusters? … or who sets the value of k ? For n points to be clustered consider the case where k=n . What is the value of the error function What happens when k = 1 ? Since we want to minimize the error why don’t we select always k = n ?

Occam’s razor and the minimum description length principle Clustering provides a description of the data For a description to be good it has to be: Not too general Not too specific Penalize for every extra parameter that one has to pay Penalize the number of bits you need to describe the extra parameter So for a clustering C , extend the cost function as follows: NewCost(C) = Cost( C ) + |C| x logn

Lect4

More Related Content

Lect4