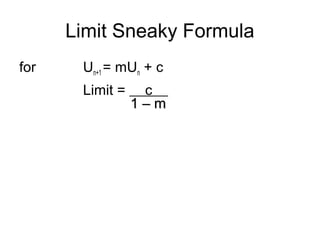Linear recurrence relations limits
- 1. Block 1 Linear Recurrence Relations Limits
- 2. What is to be learned? • When linear recurrence relations have a limit • How to calculate the limit • How to interpret the results
- 3. Consider Un+1 = 0.5Un + 8 U0 = 10 U1 = 0.5(10) + 8 = 13 U2 = 0.5(13) + 8 = 14.5 U3 = 15.25 U4 = 15.625 U5 = 15.813 U6 = 15.906 U7 = 15.953 U8 = 15.977 U9 = 15.988 UU1111 = 15.997= 15.997 UU1212 = 15.999= 15.999 UU1313 = 15.999= 15.999 UU1414 = 16.000= 16.000 UU1515 = 16.000= 16.000 ““Reaches” aReaches” a limit of 16limit of 16
- 4. Un+1 = 0.5Un + 8 U14 = 16, U15 = 16 Limit = 16 U15 = 0.5(16) + 8 = 16 U16 = 0.5(16) + 8 = 16 etc. Limit of 16 means does not go over 16
- 5. When is there a Limit? for recurrence relation Un+1 = mUn + c goes to limit if -1 < m < 1
- 6. Finding the Limit Un+1 = 0.5Un + 8 -1 < m < 1 so as n∞ Equation becomes L = 0.5L + 8 -0.5L -0.5L 0.5L = 8 L = 8 /0.5 = 16 UUnnUUn+1n+1 Limit LLimit L
- 7. When is there a Limit? for recurrence relation Un+1 = mUn + c goes to limit if -1 < m < 1
- 8. Finding the Limit Un+1 = 0.8Un + 10 -1 < m < 1 so as n∞ Equation becomes L = 0.8L + 10 -0.8L -0.8L 0.2L = 10 L = 10 /0.2 = 50 UUnnUUn+1n+1 Limit LLimit L
- 9. Key Question Un+1 = 0.2Un + 20 -1 < m < 1 so as n∞ Equation becomes L = 0.2L + 20 -0.2L -0.2L 0.8L = 20 L = 20 /0.8 = 25 UUnnUUn+1n+1 Limit LLimit L
- 10. Ex Paul Uter’s factory dumps 200kg of yuk at the end of each day into the nearby loch. The council install a filter scheme that removes 30% of the yuk each day If the yuk exceeds 700kg, Tony trout and his pals will perish horribly Is Tony safe? loch yukloch yuk outout –– 30%30% InIn + 200+ 200 YYn+1n+1 = 0.7Y= 0.7Ynn + 200+ 200 X 0.7X 0.7 Yn X 0.7X 0.7 + 200+ 200 Yn+1
- 11. -1 < m < 1 so as n∞ Equation becomes L = 0.7L + 200 -0.7L -0.7L 0.3L = 200 L = 200 /0.3 = 666.7Kg of yuk After a period of time there will be a limit of 666.7 Kg at the start of each day. Tony and pals are safe! YYnnYYn+1n+1 Limit LLimit L YYn+1n+1 = 0.7Y= 0.7Ynn + 200+ 200
- 12. Ex Bertie’s balloon has sprung a leak. It is losing 20% of its air each hour. To compensate Bertie pumps 10m3 into it at the end of each hour. If volume of air drops below 45m3 , the balloon will crash. Is Bertie doomed? air volumeair volume outout –– 20%20% InIn + 10+ 10 VVn+1n+1 = 0.8V= 0.8Vnn + 10+ 10 (X 0.8)(X 0.8) Vn X 0.8X 0.8 + 10+ 10 Vn+1
- 13. -1 < m < 1 so as n∞ Equation becomes L = 0.8L + 10 -0.8L -0.8L 0.2L = 10 L = 10 /0.2 = 50m3 After a period of time there will be a limit of 50m3 at the start of each hour. Bertie is safe! VVnnVVn+1n+1 Limit LLimit L VVn+1n+1 = 0.8V= 0.8Vnn + 10+ 10 or is he?or is he?
- 14. -1 < m < 1 so as n∞ Equation becomes L = 0.8L + 10 -0.8L -0.8L 0.2L = 10 L = 10 /0.2 = 50m3 After a period of time there will be a limit of 50m3 at the start of each hour. Bertie is safe! VVnnVVn+1n+1 Limit LLimit L VVn+1n+1 = 0.8V= 0.8Vnn + 10+ 10 or is he?or is he? will not gowill not go aboveabove 5050
- 15. Volume at start of hour = 50m3 During next hour V = 0.8(50) + 10 = 40 VVn+1n+1 = 0.8V= 0.8Vnn + 10+ 10 + 10
- 16. Volume at start of hour = 50m3 During next hour V = 0.8(50) + 10 = 40 + 10 Will drop below 45 during the hour Nae luck Bertie VVn+1n+1 = 0.8V= 0.8Vnn + 10+ 10
- 17. Limit Sneaky Formula for Un+1 = mUn + c Limit = c 1 – m1 – m
- 18. Henry’s hedge is causing a bit of annoyance to his neighbor Brutal Boris. His hedge is increasing is height by 80cm each year. To compensate Henry cuts 30% from the height if the hedge each June. Boris has said that if the height exceeds 2m then he will do Henry some serious mischief. Should Henry be worried? Hn+1 = 0.7Hn + 80 -1 < m < 1 so as n∞ L = 0.7L + 80 0.3L = 80 L = 266 2 /3 cm Not good for Henry! HHnnHn+1Hn+1 Limit LLimit L Key Question