lsh

近似近傍点探索手法 Locality Sensitive Hashing

( 最 ) 近傍点探索 ( Nearest Neighbor Search) とはいわゆる、特徴空間内での類似データ探索二種類の問題が考えられる定義 ℜ d 空間上の点集合 P が与えられた場合最近傍点探索クエリ点 q に対し、 p∈P で、 ||p-q|| を最小とする点 p を求める問題 r- 近傍点探索クエリ点 q に対し、 p∈P で、 ||p-q||<r となる点 p を ( 存在するのならば ) 列挙する問題

近傍点探索問題近傍点探索アルゴリズムは、以下のようなタスクにおいて利用されるインスタンスベース学習(k-近傍法) クラスタリングデータセグメンテーションデータベース検索最短経路木探索(Minimum Spanning Tree) データ圧縮類似データ検索

近傍点探索アルゴリズム最も単純なものは、クエリ点 q と、 p∈P の点全ての距離を求め、最も近い点を探す ( 線形探索法 ) 計算量は O(NlogN) 単純に考えて、 P のインスタンス数に比例する N-1 回の距離計算が必要インスタンス数が大きくなればなるほど、計算量も必要空間量も大きくなる

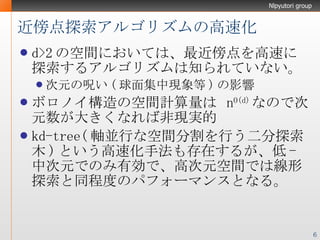
近傍点探索アルゴリズムの高速化 R d 空間においての近傍点探索では、 d≦2 の場合においては、高速な最近傍点探索アルゴリズムが知られている。 d=2 の場合には、例えばボロノイ図をたどることによって可能 (Kanda et al, 2002) 空間計算量 O(n) 計算量 O(log N) Voronoi diagram From wikipedia http://ja.wikipedia.org/wiki/%E7%94%BB%E5%83%8F:Coloured_Voronoi_2D.png

近傍点探索アルゴリズムの高速化 d>2 の空間においては、最近傍点を高速に探索するアルゴリズムは知られていない。次元の呪い ( 球面集中現象等 ) の影響ボロノイ構造の空間計算量は n O(d) なので次元数が大きくなれば非現実的 kd-tree( 軸並行な空間分割を行う二分探索木 ) という高速化手法も存在するが、低 - 中次元でのみ有効で、高次元空間では線形探索と同程度のパフォーマンスとなる。

近似近傍点探索問題高次元ベクトル空間において、純粋な最近傍点探索を高速化する手法は存在しない ( まだ知られていない ) そこで、純粋な近傍点探索ではなく、確率的に近似的な近傍点探索を行う手法の研究が進められている。 Approximate Nearest Neighbor (Araya et al 1998) Locality-Sensitive Hashing (Indyk et al 1998) Metric trees (Moore et al 2003)

近似近傍点探索問題の定義近似近傍点探索問題に関して、 Indyk らは、 c- 近似 R- 最近傍点探索という問題を定式化した。以下、 (r,c)- 近似最近傍点探索定義 R d 空間上の点集合 p∈P が与えられたとする If : クエリ点 q に対して、 p∈P で ||p-q||<r となる点が存在するならば then : p’∈P で、 ||p’-q||< c r となる点集合を返す (c≧1) 本当は r 以内のものだけが欲しい！ crの中に含まれているものを列挙できれば最近傍も含む ||p-q||<rの点は得られる q r cr

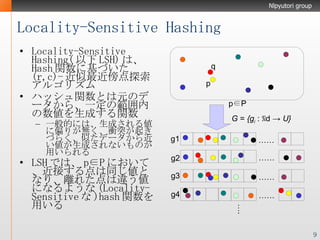
Locality-Sensitive Hashing Locality-Sensitive Hashing( 以下 LSH) は、 Hash 関数に基づいた (r,c)- 近似最近傍点探索アルゴリズムハッシュ関数とは元のデータから、一定の範囲内の数値を生成する関数一般的には、生成される値に偏りが無く、衝突が起きづらく、似たデータから近い値が生成されないものが用いられる LSH では、 p∈P において、近接する点は同じ値となり、離れた点は違う値になるような ( Locality-Sensitive な )hash 関数を用いる p q p∈P G = {g i : ℜd -> U} …… g1 …… g2 …… g3 …… g4 ….

LS-Hash 関数の定義対象とするもとの空間を ℜ d 、生成される空間を U とする関数 h が以下の条件を満たす場合、局所鋭敏な ( Locality-Sensitive な ) 関数と定義される ||p-q||<r の時、 Pr[h(p)=h(q)] が p 1 以上 ||p-q||≧cr の時、 Pr[h(q)=h(q)] が p 2 以下 (p 2 <p 1 ) 上記条件を満たす L 個のハッシュ関数 G{h 1 ,h 2 …h k } が与えられたとき、一定確率以上 (≧1/2) で L 個のバケット探索によって (r,c)- 近似最近傍点探索を達成する ( 最近傍を見つける ) 方法が存在するただし、 L=N ρ(c) ρ(c)=log(1/p 1 )/log(1/p 2 ) K=log(n)/log(1/p 2 ))

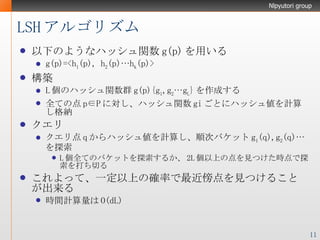
LSH アルゴリズム以下のようなハッシュ関数 g(p) を用いる g(p)=<h 1 (p), h 2 (p)…h k (p)> 構築 L 個のハッシュ関数群 g(p){g 1 ,g 2 …g L } を作成する全ての点 p∈P に対し、ハッシュ関数 gi ごとにハッシュ値を計算し格納クエリクエリ点 q からハッシュ値を計算し、順次バケット g 1 (q),g 2 (q)… を探索 L 個全てのバケットを探索するか、 2L 個以上の点を見つけた時点で探索を打ち切るこれよって、一定以上の確率で最近傍点を見つけることが出来る時間計算量は O(dL)

LSH Hash Family LSH スキームでは、用いる距離尺度に応じて、関数 h を構築する必要がある以下の距離尺度において LSH 関数が提案されている L 1 ノルム (Hamming 距離 ) (Gionis et al, 1999) Cosine 尺度 ,Earth Mover’s Distance (Charikar et al 2002) Jaccard 係数 (Broder et al, 1998) Lp ノルム (l 2 の Euclidean 距離 ) (Data et al,2004,Andoni et al, 2006)

LSH Hash Family Hamming 距離におけるハッシュ関数 G の定義点 p[1,2,3] から桁数を正規化した unary code 化をし、そこからランダムに選んだ bit を k 個をサンプリングする Unary(p)=011100110001 K=5 で G{h1_1,h2_3,h3_5,h4_8,h5_11} とすると G(p)= 0 1 1 1 0 01 1 00 0 1=01010 Cosine 尺度における関数 h の定義ベクトル u は、正規乱数により生成された d 次元のベクトル

LSH Hash Family for l p norm L p 空間におけるノルムの場合アイディア L p 空間上において、 p 度の安定分布により生成されたベクトルとの内積は、正規分布によってばらけはするが、元の座標を反映した値になる k 個の内積を用いた k 次元空間へのマッピングにおいては、 l2 空間においては任意の二点間の距離を定数倍の誤差で維持することが出来る [Johnson et al, 1984] L p (p>2) 空間においては、確率的にもとの空間における近傍点が、次元削減された空間において確率的に近傍点となるマッピングは存在する [Indyk et al, 2002]

LSH Hash Family for l p norm l p norm における関数の定義 a は、 p 度の安定分布により生成される乱数によって構成されたベクトル p=2 においては、平均 0, 分散 1 の正規乱数 Box-Muler 法などで生成 b は、 0 ～ w の値を持つ一様乱数から生成された値 scalar 値 b と randMax 値 w によって割って床関数を掛けることにより、 (r,c) のパラメータを調整している

参考 Piotr Indyk Near-Optimal Hashing Algorithms for Approximate Near(est) Neighbor Problem http://people.csail.mit.edu/indyk/mmds.pdf

lsh

More Related Content

lsh