Maps-and-map-interpretation.pdf
- 1. Maps and map interpretation An introduction for geoscientists Produced by the University of Derby in conjunction with UKOGL
- 2. • This teaching package provides an introduction to maps and how to identify landforms using contours and cross-sections • It is designed primarily for A-Level and first year undergraduate geology and geography students who may have little experience of topographic maps, or for those who haven’t worked with them recently Aims
- 3. • Part 1 - Introduction to maps • Title • Key (sometimes called legend or explanation) • Scales • Contours • Part 2 – Map interpretation • Contour patterns • Cross-sections Contents
- 4. Part 1 - Introduction to maps • Maps are a 2-D representation of a 3-D world. They are a ‘bird’s eye’ view – as if the viewer is ‘flying’ above the land surface and looking down on it • They show how objects are distributed and their relative size • Maps are a very useful way of visualizing all sorts of data and they are a key tool for geoscientists
- 5. The same map outline can be used to show different information, so it is important to identify the map title, key, scale and orientation UK Bedrock Geology UK Annual Mean Wind Speed N N Title Key Scale North Point
- 6. Maps show how objects are distributed and their relative size © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N This is the area north of Derby that we will be focusing on later
- 7. Scales • Show the distance on the map compared to the distance on the ground • It is important to choose an appropriate map scale for the task you are undertaking • Common scales include: 1:30 000 000 (e.g. world map or atlas) 1:1 000 000 (e.g. country map) 1:50 000 (e.g. regional map) 1:10 000 (e.g. local map) • A map scale of 1:50 000 means: 1mm on the map represents 50 000mm or 50m or 0.05km on the ground
- 8. Scales with large numbers (e.g. 30 million) produce maps covering a large area in little detail https://www.cia.gov/library/publications/the-world-factbook/docs/refmaps.html
- 9. In contrast, on a 1:50 000 map, individual buildings, minor roads and contours are evident N © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. 1 km
- 10. 200 km N The scale bar shows a measurement on the map and the specific distance it represents on the ground © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. 1 km Galway to Dublin is about 200 km Cowers Lane to Shottlegate is about 1 km N
- 11. Contours • Contours are lines joining points of equal value. This value on topographic maps is height (or elevation/altitude) above mean sea level (MSL) • Each successive contour represents an increase or decrease in constant value. Often every 5th contour will be in bold to help identification • Contours are normally associated with changes in height, but they can represent any parameter (e.g. thickness, pressure, rainfall). They can also be called iso-lines (e.g. isopachs, isobars, isohyets)
- 12. Contours show the distribution and relative size of any measured value Surface air pressure is measured in millibars and is shown here as isobars
- 13. Contours can show the distribution and relative size of any measured value This map shows the thickness of the Earth’s crust (in kms) This map shows rainfall data for Australia (in mm)
- 14. N © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. 1 km Let’s return to topographic maps - on the map the land surface looks flat, but the contours indicate otherwise View from Point X towards the SW, showing a valley and a hill in the distance X
- 15. Contours never cross and will at some point close, although this may be off the map. Topographic contours that close in concentric patterns delineate hills or depressions 1 km
- 16. Contours are drawn perpendicular to the maximum slope, with the spacing between contours indicating the steepness of the slope 1 km
- 17. Based on the shape of contours, landforms such as valleys and ridges can be recognised Valley and stream Ridge 1 km
- 18. 40m 30m 20m 10m 0 MSL This image highlights the real shape of two hills and how they are shown on a contour map Image from OS Map reading made easy. https://www.ordnancesurvey.co.uk/resources/map-reading/index.html
- 19. You can watch a video explaining how to read contour lines on an Ordnance Survey map Click here to play… The Ordnance Survey website has further information on all aspects of maps and map reading, including how to work out grid references and take compass bearings https://www.ordnancesurvey.co.uk/resources/map-reading/index.html
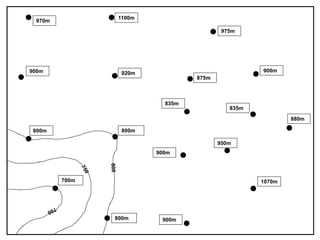
- 20. Practical exercise 1 Drawing contours
- 22. 800m 800m 700m 800m 700m 900m 750m 800m 850m Then join up all the original and interpolated points of equal value to form contours. Start by interpolating between individual points, labelling new values as you go. 750m 750m 750m The easiest way to draw a contour map based on spot heights is to simply interpolate between the known values. As you interpolate between points make sure you label the new values, as it quickly becomes very confusing if you don’t! Then join identical values with smooth curves to create contours that simulate topography
- 24. Completing the contouring exercise • Based on the contour map you have created: • Where is the highest ground? • Where is the lowest area? • Describe the major landforms • Mark on the most likely course of a stream and determine in which direction it is flowing
- 26. Part 2 – Map interpretation • Contour patterns can be used to recognise distinctive landforms such as ridges, valleys and hills • Contours may appear as black or coloured lines on maps, and are often supported by colour shading to give an impression of relief • Cross-sections provide a useful way of visualizing the shape of the land surface, but care needs to be taken in their construction, particularly in terms of vertical exaggeration
- 27. © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N 1 km Previously we looked at the topography in this area – let’s take a closer look at the contours
- 28. What is the contour interval? Locate the 150m contour between Shottle and Blackbrook 150m contour © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N 1 km The contour interval is 10m with bold lines every 50m
- 29. If you walked along this contour, what would your route be like? Flat, as long as you remain on the 150m contour 150m contour © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N
- 30. Which direction is downhill from the 150m contour? 150m contour © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N 200m contour 100m contour Downhill
- 31. What else about the contours help to determine the direction of slope? © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N The contour values are perpendicular to the slope, with the bottom of the number on the downhill side
- 32. What does the hillside look like if you stand at Point A and look towards Point B? B A © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N 1 km It would go downhill to the stream and then uphill again to Point B
- 33. 100 200 300 400 500 600 700 800 900 100 200 A B Contour value (metres) Distance (metres) Valley with stream 0 No vertical exaggeration This image shows a similar valley in the area, confirming the gentle slope angles A useful technique to visualise landforms is to draw a cross-section. This one is between Points A and B on the previous map The X axis represents distance and the Y axis height
- 34. 100 200 300 400 500 600 700 800 100 200 A B Contour value (metres) Distance (metres) Valley with stream 0 2x vertical exaggeration When drawing cross-sections it is important to be aware how the scales affect your perception of slope angle The purpose will dictate the scales you use. If the cross- section is to highlight relative changes in topography then a vertical exaggeration is fine, despite the fact that it increases the angles of all sloping lines If there is a need to add sub- surface geology or calculate true slope angles, then there should be no vertical exaggeration
- 35. Notice how the change in vertical exaggeration affects the angles of slope Bear this in mind when drawing your own cross- sections and decide how much (if any) vertical exaggeration is required Compare the effects of vertical exaggeration on the same cross-section
- 36. You now know how to identify a sloping valley by the shape of the contours. © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N Uphill They form a V-shape that points uphill
- 37. There are lots of valleys on the map; mark them with an arrow pointing in the downhill direction Arrows indicate downhill direction of valleys © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N
- 38. Notice that all the rivers are in valleys, but not all the valleys have a river. Why is this the case? © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N Arrows indicate downhill direction of valleys
- 39. What feature do the contours in the red area represent? © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N A broad, N-S trending ridge
- 40. It may help if you imagine you are standing at Point C on the 150m contour, looking towards Point D. Would you be able to see Point D? We can draw a cross-section to confirm our idea © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N C D Axis of ridge
- 41. 100 200 300 400 500 600 100 200 C D Contour value (metres) Distance (metres) Ridge Cross-section showing the broad, gentle ridge between Points C and D 0 2x vertical exaggeration Standing at Point C you would be unable to see Point D because the crest of the ridge is higher than Point D Here some vertical exaggeration is appropriate because the relief is very subtle
- 42. Practical exercise 2 Constructing cross-sections
- 43. A A’ Before constructing a cross- section, look at the contours and try to imagine what the surface topography looks like Closely spaced contours showing a steep slope Widely spaced contours showing less steep slopes compared to those in the east Narrower range of contours between 140-160m indicate a relatively flat hill top We will now draw our own cross- section between Cowers Lane (A) and Chevinside (A’)
- 44. A A’ Use graph paper to mark on every time a contour crosses the chosen line of section 85 90 95 100 105 110 150m 200m 100m 50m Label each contour height and plot the value directly onto the Y-axis of the cross-section
- 45. A A’ Once all the contour heights along the section have been plotted the land surface can be added 50m 100m 150m 200m This surface should be drawn free hand to give a natural shape that honours the contours 4x vertical exaggeration
- 46. 150m 100m 50m 0 200m A A’ 1 km 2 km 3 km A completed cross-section between A-A’ The vertical scale has been exaggerated in order to show the subtle relief. To calculate the vertical exaggeration, divide the horizontal scale (1cm to 200m) by the vertical scale (1cm to 50m) So, 200/50 = 4x vertical exaggeration West East Scale 1: 20 000 4x vertical exaggeration
- 47. Comparison between a vertically exaggerated section and a true scale cross-section 200m 0 No vertical exaggeration 100m 150m 50m 200m 0 4x vertical exaggeration The vertically exaggerated section provides a clearer representation of subtle landforms, the other a true representation of slope angles
- 48. You have now been introduced to the basic elements of topographic maps You have used contours to identify common landforms and begun to visualise them in 3-D You can now construct cross-sections and understand the concept of vertical exaggeration Learning outcomes
- 49. Slide 50: print out at A4, in B/W, portrait format Slide 51: print out at A4, in colour, portrait format Slide 52: print out at A4, in colour, portrait format Graph paper for constructing the cross-section Handouts required for the practicals
- 51. © Crown Copyright/database right 2014. An Ordnance Survey/EDINA supplied service. N 1 km
- 52. A A’