Mathematical investigation

.
.
..
.
.
.
.
.
.
.
.
.
Points Polygon Chords Intersection
4 quadrilateral 6 1
5 pentagon 10 5

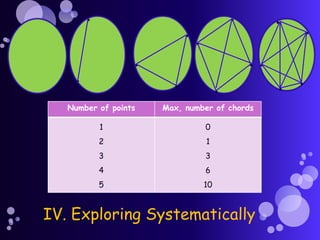
Number of points Max, number of chords
1
2
3
4
5
0
1
3
6
10
.
.
.
.
.
.
.
.
.
.
.
.
.
.
IV. Exploring Systematically

Number of Points Max. Number of
regions
1
2
3
4
5
1
2
4
8
16

Number of
Points
Max.
Number of
Chords
Max. number
of regions
1
2
3
4
5
0
1
3
6
10
1
2
4
8
16

Number of points Max. no. of
chords
1
2
3
4
5
O
1
3 = 1 + 2
6 = 1 + 2 + 3
10 = 1+ 2 + 3 + 4

Number of points Max. number of chords
1
2
3
4
5
This suggested
that for n
0
1 2 x ½ 2 x ½
3 3 x 1 3 x 2/2 3 x (3-1)/2
6 4 x 1 ½ 4 x 3/2 4 x (4-1)/2
10 5 x 2 5 x 4/2 5 x (5-1)/2
n x (n-1)/2

Number of points Max. number of regions
1
2
3
4
5
This suggested that for n
1 20 21-1
2 21 23-1
4 22 2 3-1
8 23 24-1
16 24 25-1
2n-1
For the number of regions, and
observable pattern is the following:

Data from diagram Data from
conjecture
Number of points Max. number of
chords
n x (n-1)/2
1
2
3
4
5
0
1
3
6
10
1x(1-1)/2 = 0
2x(2-1)/2 = 1
3x(3-1)/2 = 3
4x(4-1)/2 = 6
5x(5-1)/2 = 10
In each instances, the value obtained from the
conjecture agrees with that obtained from the
diagrams so the conjecture is supported.

..
.
.
..
At this stage, the conjecture has been
tested and supported, but not justified.

Data from
diagram
Data from
conjecture
Number of points Max. number of
chords
2n-1
1
2
3
4
5
1
2
4
8
16
21-1
22-1
23-1
24-1
25-1

Mathematical investigation

More Related Content

Mathematical investigation