Microwave advancement

Plasma Devices and Operations
Vol. 17, No. 2, June 2009, 98–116

Advancements of microwave diagnostics in magnetically
confined plasmas
A. Masea *, Y. Kogia , N. Itoa , Y. Yokotaa , K. Akakia , K. Kawahatab , Y. Nagayamab , T. Tokuzawab ,
S. Yamaguchic , H. Hojod , N. Oyamae , N.C. Luhmann, Jrf , H.K. Parkg and A.J.H. Donnéh
a Art, Science and Technology Center for Cooperative Research, Kyushu University, Kasuga 816-8580,
Japan; b National Institute for Fusion Science, Toki, Gifu 509-5292, Japan; c Faculty of Engineering
Science, Kansai University, Suita, Osaka 564-8680, Japan; d Plasma Research Center, University of
Tsukuba, Tsukuba 305-8577, Japan; e Naka Fusion Institute, Japan Atomic Energy Agency, Naka
311-0193, Japan; f Department of Electrical and Computer Engineering, University of California,
Davis, CA 95616, USA; g Department of Physics, Pohang University of Science and Technology,
Pohang 790784, South Korea; h FOM-Instituut voor Plasmafysica Rijnhuizen,
c/o Institut fur Plasmaphysik, Julich D42525, Germany

(Received 15 March 2009; final version received 17 March 2009 )

Microwave to millimeter-wave diagnostic techniques such as interferometry, reflectometry, scattering and
radiometry have been powerful tools for diagnosing magnetically confined plasmas. Recent advances in
electronic devices and components together with computer technology have enabled the development of
advanced diagnostics in microwave to millimeter-wave region. The two-dimensional and three-dimensional
profiles of plasma density/temperature and dynamic behaviors of their fluctuations are measured by using
the advanced diagnostic systems. The measurements have clarified the physics issues such as stability, wave
phenomena and fluctuation-induced transport. We report here on the representative microwave diagnostics
and their contribution to plasma confinement physics.

Keywords: microwave; interferometry; reflectometry; ECE; plasma diagnostics; magnetic confinement
system

1. Introduction

Transmission, reflection, scattering and radiation processes of electromagnetic waves are used as
diagnostic tools of plasmas. In magnetically confined plasmas, since various specific frequencies
such as the cutoffs and resonances in plasmas determined by confining magnetic fields and electron
densities are in the range of 10–300 GHz, the optimum probing wavelengths are in the range
of microwave to millimeter-wave. The diagnostic techniques are interferometry, reflectometry,
scattering and electron cyclotron emission (ECE). The parameters obtained by these diagnostic
techniques are the equilibrium and fluctuation components of electron density, temperatures and

*Corresponding author. Email: mase@astec.kyushu-u.ac.jp

ISSN 1051-9998 print/ISSN 1029-4929 online
© 2009 Taylor & Francis
DOI: 10.1080/10519990902909436
http://www.informaworld.com

Plasma Devices and Operations 99

magnetic field. These parameters are measured to clarify the important issues of plasma physics
such as stability, wave phenomena and fluctuation-induced transport.
Recently, theoretical understanding of plasma turbulence and anomalous transport has been
greatly enriched with the help of the rapid advancement of computer technology, which has made it
possible by extensive computer simulations to reveal three-dimensional (3D) structures of plasma
turbulence. However, the behavior of the turbulence remains poorly understood experimentally,
which prevents the advent of efficient means of turbulence suppression and improvement of
plasma confinement. Recent advances in microwave and millimeter-wave technology together
with computer technology have enabled the development of new generation of diagnostics for
visualization of two-dimensional (2D) to 3D structures of plasmas. Microwave/millimeter-wave
radar and imaging are expected to be one of the promising diagnostic methods for this purpose.
We present here the recent advancements in microwave/millimeter-wave diagnostics and physics
results obtained in magnetically confined plasmas.

2. Microwave diagnostic techniques

2.1. Interferometry

A heterodyne interferometer with two oscillators having different frequencies or one oscillator
and a single-sideband converter is used to determine the phase shift between transmitted and
reference beams. For the latter case, the same oscillator is used as an incident wave and a local
oscillator (LO) as shown in Figure 1. One of the waves passing through a directional coupler
is shifted by fIF using a single-sideband up-converter. The transmitted wave and the reference
wave are down-converted to an intermediate frequency (IF) signal. The measurement of the phase
shift due to the interaction with plasma can be performed at the frequency fIF without loss of
accuracy. A two-color interferometer having two probe beams with different frequencies is often
used in large size of machines in order to avoid the mechanical vibration along the beam path.
The antennas must be capable of launching waves at different frequencies.
A sufficient number (8–12) of probing chords are needed to obtain a reconstruction of density
profiles. When enough power is obtained as an incident source, power splitters can be used to divide
the incident signal into a number of independent probing beams, otherwise, separate oscillators

Figure 1. Heterodyne interferometer using an upconverter.

100 A. Mase et al.

Figure 2. Phase imaging interferometer installed in the GAMMA 10 tandem mirror [3].

Figure 3. Time evolution of the 2D line density proﬁles [4].


have to be employed for each probing beam. Different IFs for each channel are also employed to
avoid the crosstalk between adjacent chords.
Instead of multi-channel system, phase-imaging interferometers have been used in several
plasma experiments in order to measure multi-chord line-integrated electron densities. This tech-
nique uses a single set of optics and a detector array instead of a multi-channel optical path
with a single detector for each chord. The first example was a CO2 laser interferometer using a
15-element PbSnTe detector array, which was applied to high-density arc plasma [1]. An FIR laser
interferometer with a 20-element micro-bolometer array has been applied to tokamak plasma [2].
A millimeter-wave phase-imaging interferometer using a 4 × 4 Schottky barrier diode array has
been applied to the GAMMA 10 tandem mirror [3].
The imaging system as shown in Figure 2 is installed in the plug-cell of GAMMA 10. A
probe beam is expanded by an off-axis parabolic mirror installed inside the vacuum vessel to
cover upper-half of the plasmas. The cross-section of the probe beam is 200 × 200 mm at the
plasma center. The receiving optics, an ellipsoidal mirror, a flat mirror and polyethylene lenses
are designed by using a ray-tracing code to focus radiation signals onto the detector array. The
quadrature-type detection system provides the phase difference between two IF signals that is
proportional to the line density of the plasma.
Figure 3 shows an example of the measurement result, that is, time evolution of the 2D line-
density profiles [4]. When the electron cyclotron resonance heating (ECRH) power is applied
to the plug/barrier plasma at t = 140 ms, the confining potential is created near the position of
z = 962 cm where the magnetic field strength equals to 1 T. At the region of z = 971 cm where
the imaging system is installed, the loss particles decrease due to the effect of axial plugging.
When the ECRH is turned off at t = 190 ms, the confining potential disappears, and a short burst
appears in the line-density signal corresponding to the axial drain of the plasmas. The variation
of the profile in the axial direction is caused by the change of the magnetic field.

3. Electron cyclotron emission

3.1. Principle of ECE

The radiation from plasmas is described by the transfer equation. Since the plasmas are produced
in a vacuum chamber, it is known that the radiation intensity is modified by the effect of vacuum
wall, which is given by
1 − e−τn
In (ω) ∼ IB0
= , (1)
1 − re e−τn
where IB0 is the black body radiation given by

ω2
IB0 ∼ Nr2 3 2 κTe ,
= (2)
8π c
τn is the optical thickness of the nth harmonic of the ECE, re is the wall reflectivity (1 > re > 0.9),
Nr is the refractive index of a plasma, ω is the frequency and κ is the Boltzmann constant.
Therefore, when 1 − re τn , In nearly equals to the black body radiation. On the other hand,
when τn 1 − re , Equation (2) becomes [5]
IB0
In (ω) ∼
= τn . (3)
1 − re
Let us consider a tokamak plasma case and a coordinate system as shown in Figure 4, where
B0 is the magnetic field intensity at the plasma center and R the major radius. It is known that the

102 A. Mase et al.

Figure 4. ECE from a tokamak plasma.

toroidal magnetic field, BT , is a function of x as
R
BT = B0 . (4)
R+x
Therefore, nωce also varies accordingly. The ECE appears resonantly in width
−1
d(nωce )
xn = ωn (5)
dx
with centering on x = x(ω) which corresponds to ω = nωce . When the plasma is optically thick,
the radiation power becomes proportional to its local electron temperature. On the other hand,
when plasma is optically thin, the radiation power is proportional to both ne and Te profiles.
Therefore, when Te profile is obtained by different methods, we can determine ne profile, and vise
versa.

3.2. ECE radiometer systems

When the plasma density and temperature are sufficiently high, the plasma becomes optically thick
specifically for the fundamental O-mode and the second harmonic X-mode of ECE. The radiation
intensity of optically thick ECE harmonics reaches that of black body radiation. Therefore, the
electron temperature and its fluctuations can be diagnosed by measuring the intensity of the ECE.
In tokamak plasmas, the ECE frequency is often a monotonically decreasing function of plasma
radius toward the outboard side. Therefore, time-resolved one-dimensional (1D) temperature
profiles can be obtained by a conventional radiometer.


Several types of radiometer system have been applied to the ECE measurement of magneti-
cally confined plasmas, such as (i) heterodyne radiometer, (ii) Fourier-transform spectrometer,
(iii) grating polychrometer, (iv) Fabry–Perot interferometer and (v) multichannel mesh filter.
Heterodyne radiometer has good frequency resolution corresponding to spatial resolution as
well as time resolution. In the initial period, the heterodyne radiometer was not used to monitor
the entire ωce and/or 2ωce spectrum, however, since ultra-wideband mixers with full band or
octave band response have been developed, the entire ωce (2ωce ) spectrum can be measured by a
single or a few mixers.
An example of a heterodyne radiometer fabricated for the ECE measurement of KSTAR toka-
mak is shown in Figure 5 [6]. The ECE from the plasma is introduced to a diagnostics port
via two reflecting mirrors, and received by oversize or corrugated waveguides (110–162 and
164–196 GHz). Each signal is received by a conical horn independently, and fed to a pre-down
conversion box. In the pre-down conversion box of T-band (G-band) system, the signal is con-
verted to the signal with frequency up to 26.5 GHz (16 GHz) by using band-pass filters, mixers,
LOs and amplifiers. Number of the output branch from the pre-down conversion box of each
system is two. These outputs from the box are then fed to a second down conversion module for
the purpose of further down conversion. Figure 6 shows the block diagram of the second down
conversion module utilized in the T-band system.
Signals with frequency of 1–9.5, 8–14, 14–19.5 and 18–26.5 GHz at the input port are converted
to the signals with frequency up to 9.5 GHz, and fed to the output ports of IFOUT1–4, respectively.
Number of the output branch from the second down conversion module of the T-band (G-band)
system is eight (four). Then a detector module as illustrated in Figure 7(a) resolves the signal
by the band-pass filter bank with center frequencies from 2–9 GHz. We employ the microwave
integrated circuit technology to fabricate the detector module on a planar substrate. Figure 7(b)
shows an illustration of the detector module inside a nuclear instrumentation module (NIM) case.

Figure 5. (a) Heterodyne radiometer system on KSTAR, and (b) signal flow of the ECE [6].

Figure 6. Block diagram of the 2nd down conversion module [6].

104 A. Mase et al.

Figure 7. (a) Block diagram and (b) illustration of the detector module [6].

Two amplifiers, installed in the left side, are separated from main (right side) substrate in order
to adjust the amplification of the signal. The main substrate consists of a low-pass filter, a new
type eight-channel band-pass filter bank and eight video detectors. The detected signal is digitized
after a video amplifier stage.

3.3. ECE measurements in fusion experiment plasmas

The measurement of ECE has become a main diagnostic to determine temporal and spatial behav-
iors of electron temperature in fusion experiment plasmas. In toroidal plasmas, the ECE frequency
is often a monotonically decreasing function of plasma radius toward the outboard side. Therefore,
time resolved 1D temperature profiles can be obtained by a conventional radiometer. Recently,
microwave imaging technique has been applied to the ECE measurement. ECE imaging (ECEI)
is a method whereby 2D–3D images of temperature fluctuations as well as temperature profiles
can be obtained. An ECEI system was at first applied to TEXT-U, and subsequently developed
for the RTP tokamak, and more recently implemented on TEXTOR [7,8] and LHD [9]. The sys-
tem is capable of simultaneously measuring density and temperature fluctuations in the plasma
core with ∼1 cm2 resolution in the poloidal plane of TEXTOR plasmas. The ECEI system yields
the temperature and its fluctuation in an 8 × 16 matrix of sample volumes. The system views the
plasma through a large 42 × 30 cm2 quartz window. The two large-sized toroidal and poloidal
collection mirrors are used. An electroformed metal mesh beam splitter is employed to separate
the radiation at the ECE range of frequencies (95–140 GHz) from the frequencies used in the
reflectometer (70–90 GHz), which is called as microwave imaging reflectometer (MIR). Each
system utilizes a dedicated high-resolution multi-channel detector array based upon dual-dipole
antenna.


Another important key word for fusion experiments is the relativistic effect in ECE measure-
ment. It plays a major role at high electron temperatures larger than 10–20 keV. For example, in
ITER, harmonic overlap will limit the range of major radius that can be measured, the cutoffs limit
the applicability of the method at high densities and shine through will affect the measurements
at the plasma edge [10,11].

4. Reflectometry

Reflectometry has been expected to be one of the key diagnostics to measure density profiles
and density fluctuations in fusion experiment plasmas. It provides good spatial and temporal
resolutions, while requiring a single viewing chord and minimal vacuum access in contrast to
interferometry and Thomson scattering. One of the most serious problems in density profile
measurement using conventional frequency-modulation (FM) reflectometer is caused by the exis-
tence of density fluctuations in plasmas, since the multi-fringe phase changes produced by a
reflectometer are easily masked by those due to density fluctuations. Several methods have been
proposed to avoid this problem such as amplitude-modulation reflectometry or dual-frequency
differential reflectometry and pulsed-radar reflectometry using moderate short pulse or ultra-
short pulse [12–14] as well as advanced data processing techniques based on sliding fast Fourier
transform algorithm, maximum entropy method, wavelet transform and Wigner distribution.

4.1. Profile measurements

A reflectometer measures the phase difference between a probing beam propagating through a
plasma and a reference beam. The phase difference as a function of the probing frequency is
given by
rc (ω)
π
φ(ω) = 2k N (r, ω)dr − (6)
a 2
within the WKB approximation, where k and ω are the wave number and frequency of the
probing beam, N the plasma refractive index, and a and rc (ω) are the plasma and the cutoff radii,
respectively. The refractive indices of the O-mode and the X-mode propagations are given by

2 1/2
cko ωpe
No = = 1− 2
ωo ωo
1/2
ckx 2
ωpe ωx − ωpe
2 2
Nx = = 1− 2 · 2 , (7)
ωx ωx ωx − ωpe − ωce
2 2

in the cold plasma approximation, where c is the speed of light, ωpe and ωce are the electron plasma
frequency and the electron cyclotron frequency, and subscript O and X correspond to the ordinary
mode and the extraordinary mode incident waves, respectively. For the O-mode propagation, this
integral can be analytically solved for the density profile using an Abel inversion. For the X-mode
propagation, a numerical algorithm has been developed to invert the data.
Figure 8 shows the schematic of a conventional FM reflectometer. It measures the group delay
or the return phase as a function of the incident wave frequency given by

2 −1/2
dφ dω 2 rp ωpe L s − Lr
= τ (ω) , τ (ω) = 1− dr + = τp (ω) + τw (ω) (8)
dt dt c rw ω2 c

106 A. Mase et al.

Figure 8. Schematic of the reflectometer system.

for the O-mode case. We can deduce the distance to the cutoff as a function of the cutoff density.
A simple inversion procedure can be used for the O-mode radiation.
In a pulse reflectometry, a pulse modulated (∼1 ns) microwave or an impulse (10–50 ps) is used
as a probe beam. The pulse has a frequency component governed by the shape and duration. Each
Fourier component reflects from a different spatial location in the plasma. The time-of-flight for
a wave with frequency ω from the vacuum window position rw to the reflection point at rp is
given by
2 −1/2
rp ωpe
2
τ (ω) = 1− dr. (9)
c rw ω2
In order to obtain the density profile from the time-of-flight data, Equation (9) can be Abel
inverted to obtain the position of the cutoff layer,
ωpe
c τ (ω)
r(ωpe ) = · dω. (10)
π 0
2
(ωpe − ω2 )1/2

By separating different frequency components of the reflected wave and obtaining time-of-
flight measurement for each frequency component, the density profile can be determined. The
movement of the plasma position due to the fluctuations can be neglected during the reflection of
the pulse (ns to ps).

4.2. Fluctuation measurements

Reflectometry has also been used in order to study plasma fluctuations. The instantaneous phase
shift φ between the local beam and the reflected beam is expressed as φ = φ0 + δφ, where φ0
and δφ are the phase shift depending on the cutoff layer due to density and density fluctuations
of the plasma profile. In a simple homodyne reflectometer, the mixer output is given by

V = El Er cos(φ0 + δφ) = El Er (cos φ0 cos δφ − sin φ0 sin δφ)
∼ El Er (cos φ0 − δφ sin φ0 )
= (11)

assuming δφ 1, where El and Er are the electric field amplitude of the local beam and the
reflected beam, respectively. The time varying component of the mixer output depends on both
amplitude and phase modulations, since Er can be time dependent due to changes in the cutoff
layer. In general, the radial fluctuations of the cutoff layer produce the phase modulations and
the poloidal (azimuthal) fluctuations cause amplitude modulations. Therefore, it is important to
identify both phase and amplitude fluctuations using, such as, heterodyne detection or quadrature
type mixer.
In a simple 1D model, the phase changes in the O-mode and the X-mode propagations due to
the small perturbations of the density and the magnetic field, δne and δB at the critical density


layer are given by
δne
δφo ≈ 2ko Ln , (12)
ne
2kx [δne /ne + (ωce ωx /ωpe )δB/B]
2
δφx ≈ . (13)
1/Ln + (ωce ωx /ωpe )/LB
2

When the wavelength of the fluctuation is much longer than the spot size of the incident wave,
there is no attenuation or modulation of the reflected wave. The depth of the phase modulation
approaches the 1D geometric optics limit.

4.3. Reflectometer systems

One of the greatest improvement of FM reflectometry was the use of a fast sweep oscillator
such as hyper-abrupt varactor-tuned oscillator (HTO), which is used in most of the present FM
reflectometers. It can be swept wide frequency band such as 8–18 GHz in less than 10 μs. The
frequency can be converted by the use of multipliers up to 108 GHz. The ultrafast sweeping is
an important development, since the effect of fluctuations is significantly reduced. Also, it is
possible to achieve a high temporal resolution that permits to resolve fast profile changes during
the confinement transition such as ELM (edge localized mode) and ITB (internal transport barrier).
The effect of the sweep time is shown in Figure 9 [15,16]. The profile reconstructions are
performed by using two methods, the zero-cross counting and the digital phase counting by
the complex demodulation (CDM) technique. It is seen that the reconstructed profiles seem to
be improved when the sweep time is faster than 200 μs for the CDM, while the sweep time at
least faster than 20 μs seems to be necessary for the zero-cross counting. The results show that
the improvement of data analysis is important for good reconstruction; however, it is also demon-
strated that when the system performance is improved the demands on data analysis becomes
lower.

4.4. Reflectometric measurements in fusion experiment plasmas

One of the most advanced profile reflectometers are installed inASDEX-U [17,18]. The microwave
sources are HTO in the range of 8–18 GHz followed by a set of frequency multipliers to bring the
probing frequencies to the range of 16–110 GHz. The broadband reflectometry system consists of
11 FM-CW reflectometers covering the density range of 0–12.4 × 1019 m−3 on the low-field side
(five O-mode plus two X-mode channels) and 0.3–6.7 × 1019 m−3 on the high-field side (four
O-mode channels). The X-mode system gives the information of edge plasma and provides the
profile initialization for the O-mode system. The evaluation of the electron density profile is
based on the analysis of the time-frequency energy distribution of the reflected signals using the
spectrogram. A new dynamic frequency calibration method is used to take into account all existing
delays in the HTO tuning port and driver electronics. The systems are particularly important
to measure accurately the edge pedestal region of high-density ITER relevant discharges. In
Figure 10, the density profiles obtained in high-density discharges are presented and compared
with results from Thomson scattering data. The density profiles are also compared with those by
Li beam in the SOL region as shown in Figure 11.
Reflectometry has a distinct advantage of providing local measure of density fluctuations
from edge to core regions of plasmas, which enables to monitor MHD behaviors, low-frequency
instabilities and ion cyclotron range of frequency waves.
The X-mode core correlation reflectometer and O-mode reflectometer have been applied to
fluctuation measurement at the ETB (edge transport barrier) and ITB on JT-60U [19]. Figure 12

108 A. Mase et al.

Figure 9. Density profiles for various sweep times reconstructed by the zero-cross counting and the CDM methods
[15,16].

shows a schematic of the O-mode fixed frequency reflectometer. The ELM free H-mode phase is
characterized by improved confinement at the edge region together with a considerable reduction
in fluctuations. In JT-60U, such a clear transition is observed.
As shown in Figure 13(a) the frequency spectrum is changed at the transition. Figure 13(b) shows
the raw data of the edge reflectometer channel with a frequency of 34.1 GHz. The scattered signal
changes to an elongated one after the transition. An analytical method [20] using a combination of
the O-mode reflectometer and a time-dependent 2D full-wave simulation code is used to evaluate
the density fluctuation level and the value of wavenumber. The analysis suggests that the density


Figure 10. The high-field side (HFS) and the low-field side (LFS) reflectometry electron density profiles and comparison
with the vertical Thomson scattering data [17].

Figure 11. Comparison of reflectometry (REF) with lithium beam (LID) electron density profiles for two time
instants [18].

fluctuation level reduced from 1.9–3.2 to 0.29–0.44%, while the value of kθ changed from 1.6–2.0
to 0.77–0.81 cm−1 .
Zonal flows (ZFs) and associated Geodesic acoustic modes (GAMs) are turbulence-generated
time-varying Er × BT rigid poloidal plasma flows with finite radial extent. They are of major
interest for confinement since they are thought to moderate drift-wave turbulence, and hence edge
transport. Direct detection of ZFs and GAMs is challenging since they appear predominantly as
radial electric field fluctuations. It is possible to measure the plasma flow velocity using a Doppler

110 A. Mase et al.

Figure 12. Schematic of the O-mode reflectometer [19].

Figure 13. (a) Waveforms of diverter Dα intensity, NBI power PNBI , stored energy Wdia , line-averaged density of edge
interferometer, and spectrogram of edge reflectometer (35.9 GHz). (b) Lissajous of the reflectometer (top) before and
(bottom) after transition to ELM free H-mode [19].

reflectometer. Since the measured rotation velocity contains the E × B velocity, the fluctuations
in Er will appear directly as fluctuations in the Doppler shift frequency [21].
Figure 14 shows a schematic of a Doppler reflectometer and an example of analysis. The
antennas are poloidally tilted so as to create a deliberate misalignment angle θι between microwave
scattering and reflectometry, which is sensitive to the perpendicular wavenumber.

k⊥ = 2k0 sin θi . (14)


Figure 14. A schematic of a Doppler reflectometer (top), reflectometer spectra S(f ) (middle right), time evolution of
Doppler shift fD , amplitude A, and their spectra (bottom) [21].

Any poloidal motion of the density turbulence at the cutoff layer will induce a Doppler frequency
shift fD in the reflected signals,
u⊥ k⊥ 2u⊥ sin θi
fD = = . (15)
2π λ0
For edge drift-wave turbulence, E × B velocity generally dominates over the turbulence phase
velocity allowing the radial electric field Er to be extracted.
The perpendicular rotation velocity of the turbulence moving in the plasma is given by

u⊥ = vE×B + vp . (16)

For the edge, drift-wave turbulence E × B velocity generally dominates over the turbulence phase
velocity allowing the radial electric field Er to be extracted.

5. Microwave imaging diagnostics

Two types of imaging diagnostics have been developed using microwave systems, ECEI and MIR.
An ECEI is a method whereby 2D–3D images of temperature fluctuations as well as temperature
profiles can be obtained by a combination of a heterodyne receiver and detector array together
with a focusing optics for ECE signals. The ECEI system was at first applied to TEXT-U, and
subsequently developed for the RTP tokamak, and more recently implemented on TEXTOR-94
and LHD [22].
When the amplitude of fluctuations is small or the width of their wave number spectrum is
narrow, the reflected waves bear phase information on a large distance, and interpretation of

112 A. Mase et al.

the signal is straightforward. The interference of the scattered wavefronts destructs the shape
of the phase close to the cutoff position making difficult extraction of the information from the
reflectometer signal. One of the possible ways to solve the problem is to use MIR with large
aperture optics to restore the wavefronts at the receiver position. This technique can record time
history of the density fluctuations, and estimate value and spectrum of the fluctuations. The
schematics of MIR system combined with ECEI system in LHD is shown in Figure 15 [23].
Three frequencies (53, 66, 69 GHz) probe the ne fluctuations on three different cutoff layers,
corresponding to the radial width of 12 cm. An adjustable ellipsoidal mirror as shown in Figure 16
is installed in the vacuum in order to control the illumination angle. The mirror angles are remotely
controlled by non-magnetic actuators with ultrasonic motors. Separation between the illumination
and the detection optics reduces the back ground noise due to the stray wave. The difference of
the optimum angle is one degree between the X and O modes. Note that the adjustment of the
mirror angle is extremely important for the LHD experiment as shown in Figure 16.
An MHD mode with equally separated higher harmonics has been observed in the LHD plasma
in the case of perpendicular ion heating as shown in Figure 17. The mode appears as the density

Figure 15. Schematic of the microwave imaging system on LHD.

Figure 16. Adjustable mirror in side the vacuum system.


Figure 17. Time frequency spectra obtained by (a) MIR and (b) magnetic probe [23].

and magnetic ﬂuctuations with fundamental frequency of 1 ∼ 10 kHz. The mode is destabilized
by both high-energy ion and pressure gradient at the rational surface.

6. Collaboration research program by remote participation of the experiment

In large fusion experiment program, such as the ITER project, the remote participation at the
experiment is extremely important for the success of the project. In Japan, it has been started
from January 2002 via an internet called super science information network (Super-SINET). The
Super-SINET is an ultrahigh-speed network intended to develop and promote Japanese academic
researches by strengthening collaboration among leading academic research institutes. The inter-
net backbone connects research institutes at 10 Gbps, and the leading research facilities in each
institute are directly connected at 1 Gbps. The remote experiment system has been introduced to
the ultrashort-pulse reﬂectometry (USRM) system in LHD [24].
Figure 18 shows the schematic of the USRM system [25]. An impulse generator is utilized as
a source. The pulse width, height and repetition rate of the impulse are 22 ps, 3 V and 1 MHz,

Figure 18. Schematic of the USRM system using Super SINET.

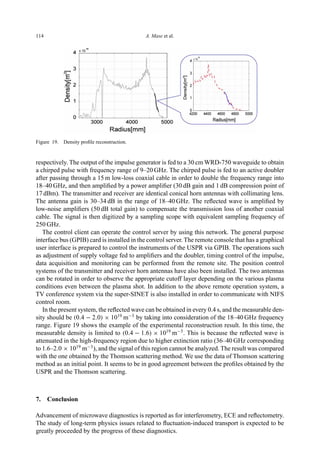
114 A. Mase et al.

Figure 19. Density profile reconstruction.

respectively. The output of the impulse generator is fed to a 30 cm WRD-750 waveguide to obtain
a chirped pulse with frequency range of 9–20 GHz. The chirped pulse is fed to an active doubler
after passing through a 15 m low-loss coaxial cable in order to double the frequency range into
18–40 GHz, and then amplified by a power amplifier (30 dB gain and 1 dB compression point of
17 dBm). The transmitter and receiver are identical conical horn antennas with collimating lens.
The antenna gain is 30–34 dB in the range of 18–40 GHz. The reflected wave is amplified by
low-noise amplifiers (50 dB total gain) to compensate the transmission loss of another coaxial
cable. The signal is then digitized by a sampling scope with equivalent sampling frequency of
250 GHz.
The control client can operate the control server by using this network. The general purpose
interface bus (GPIB) card is installed in the control server. The remote console that has a graphical
user interface is prepared to control the instruments of the USPR via GPIB. The operations such
as adjustment of supply voltage fed to amplifiers and the doubler, timing control of the impulse,
data acquisition and monitoring can be performed from the remote site. The position control
systems of the transmitter and receiver horn antennas have also been installed. The two antennas
can be rotated in order to observe the appropriate cutoff layer depending on the various plasma
conditions even between the plasma shot. In addition to the above remote operation system, a
TV conference system via the super-SINET is also installed in order to communicate with NIFS
control room.
In the present system, the reflected wave can be obtained in every 0.4 s, and the measurable den-
sity should be (0.4 − 2.0) × 1019 m−3 by taking into consideration of the 18–40 GHz frequency
range. Figure 19 shows the example of the experimental reconstruction result. In this time, the
measurable density is limited to (0.4 − 1.6) × 1019 m−3 . This is because the reflected wave is
attenuated in the high-frequency region due to higher extinction ratio (36–40 GHz corresponding
to 1.6–2.0 × 1019 m−3 ), and the signal of this region cannot be analyzed. The result was compared
with the one obtained by the Thomson scattering method. We use the data of Thomson scattering
method as an initial point. It seems to be in good agreement between the profiles obtained by the
USPR and the Thomson scattering.

7. Conclusion

Advancement of microwave diagnostics is reported as for interferometry, ECE and reflectometry.
The study of long-term physics issues related to fluctuation-induced transport is expected to be
greatly proceeded by the progress of these diagnostics.


Acknowledgements
This work is performed as a collaborating research program at National Institute for Fusion Science (NIFS04KCHH002),
and is also partly supported by the Grant-in-Aid for Scientific Research, the Ministry of Education, Science, Sports and
Culture (No. 16082205 and 20360186).

References

[1] C.A.J. Hugenholtz and B.J.H. Meddens, Multichannel CO2 -laser interferometer using a PbSnTe detector array,
Rev. Sci. Instrum. 53 (1982), pp. 171–174.
[2] P.E. Young, D.P. Neikirk, P.P. Tong, D.B. Rutledge, and N.C. Luhmann, Jr, Multichannel far-infrared phase imaging
for fusion plasmas, Rev. Sci. Instrum. 56 (1985), pp. 81–89.
[3] N. Oyama, A. Mase, T. Tokuzawa, K. Imamura, A. Itakura, T. Tamano, Y. Harada, and K. Mizuno, Millimeter-wave
two-dimensional imaging array for the GAMMA 10 tandem mirror, Rev. Sci. Instrum. 68 (1997), pp. 500–502.
[4] A. Mase, Y. Kogi, A. Yamamoto, M. Ohashi, S. Osako, L.G. Bruskin, and H. Hojo, Development and application of
millimeter-wave imaging radar, J. Plasma Fusion Res. 78 (2002), pp. 439–446.
[5] G. Bekefi, Radiation Processes in Plasmas, Wiley, New York, 1966.
[6] Y. Kogi, T. Sakoda, A. Mase, N. Ito, Y. Yokota, S. Yamaguchi, Y. Nagayama, S.H. Jeong, M. Kwon, and K. Kawahata,
Development of multi-channel IF system for ECE radiometer on KSTAR tokamak, Rev. Sci. Instrum. 79 (2008),
10F115/1–3.
[7] H.K. Park, N.C. Luhmann, Jr, A.J.H. Donné, I.G.J. Classen, C.W. Domier, E. Mazucatto, T. Munsat, M.J. van de
Pol, Z. Xia, and TEXTOR team, Observation of high-field side crash and heat transfer during sawtooth oscillation
in magnetically confined plasmas, Phys. Rev. Lett. 96 (2006), 195003.
[8] H.K. Park, A.J.H. Donné, N.C. Luhmann, Jr, I.G.J. Classen, C.W. Domier, E. Mazucatto, T. Munsat, M.J. van de Pol,
Z. Xia, and TEXTOR team, Comparison study of 2D images of temperature fluctuations during sawtooth oscillation
with theoretical models, Phys. Rev. Lett. 96 (2006), 195004.
[9] A. Mase, Y. Kogi, H. Hojo, M. Yoshikawa, A. Itakura, T. Cho, T. Tokuzawa, K. Kawahata, Y. Nagayama,
N. Oyama, et al., Progress in microwave diagnostics and physics issues in magnetically confined plasmas, Trans.
Fusion Sci. Tech. 51 (2007), pp. 52–57.
[10] M. Bornatici and U. Ruffina, ECE Diagnostic on ITER in the presence of superthermals, in Diagnostics for Experi-
mental Thermonuclear Fusion Reactors, 2nd ed., P. Stott, G. Gorini, P. Prandoni, and E. Sindoni, eds., Plenum, New
York and London, 1998, pp. 181–184.
[11] H.J. Hartfuss, R. Konig, and A. Werner, Diagnostics for steady state plasmas, Plasma Phys. Control. Fusion 48
(2006), pp. 83–150.
[12] J. Sanchez, B. Branas, T. Estrada, E. de la Luna, and V. Zhuravlev, Amplitude modulation reflectometry for large
fusion devices, Rev. Sci. Instrum. 63 (1992), pp. 4654–4656.
[13] A.J.H. Donné, S.H. Heijnen and C.A.J. Hugenholtz, Pulsed radar reflectometry and prospects for fluctuation
measurements, Fusion Eng. Des. 34–35 (1997), pp. 73–80.
[14] C.W. Domier, N.C. Luhmann, Jr, A. Chou, W.-M. Zhang, and A.J. Romanowsky, Ultrashort-pulse reflectometry,
Rev. Sci. Instrum. 66 (1995), pp. 399–401.
[15] T. Tokuzawa, A. Mase, N. Oyama, A. Itakura, and T. Tamano, Ultrafast broadband frequency-modulation
reflectometer for density profile measurements in GAMMA 10, Rev. Sci. Instrum. 68 (1997), pp. 443–445.
[16] A. Mase, T. Tokuzawa, L.G. Bruskin, Y. Kogi, N. Oyama, S. Kubota, T. Onuma, N. Goto, A. Itakura, H. Hojo, et al.,
Density profile and fluctuations measurements using microwave reflectometry, J. Plasma Fusion Res. 74 (1998),
pp. 1189–1200.
[17] P. Varela, M.E. Manso, A. Silva, The CFN team, and the ASDEX upgrade team, Review of data processing techniques
for density profile evaluation from broadbamd FM-CW reflectometry on ASDEX upgrade, Nucl. Fusion 46 (2006),
pp. S693–S707.
[18] A. Silva, M. Manso, P. Varela, L. Cupido, and L. Meneses, Recent improvements of the broadband FMCW
reflectometry system for density profile measurements on ASDEX upgrade, Rev. Sci. Instrum. 77 (2006),
10E932.
[19] N. Oyama, L.G. Bruskin, H. Takenaga, K. Shinohara, A. Isayama, S. Ide, Y. Sakamoto, T. Suzuki, T. Fujita,
Y. Kamada, and Y. Miura, Density fluctuation measurement at edge and internal transport barriers in JT-60U,
Plasma Phys. Control. Fusion 46 (2004), pp. A355–A362.
[20] L. Bruskin, N. Oyama, A. Mase, K. Shinohara, and Y. Miura, Reconstruction of wavenumber spectra of plasma
turbulence in microwave reflectometry, Plasma Phys. Control. Fusion 46 (2004), pp. 1313–1330.
[21] D. Conway, B. Scott, J. Schirmer, M. Reich, A. Kendl, and the ASDEX Upgrade Team, Direct measurement of
zonal flows and geodesic acoustic mode oscillations in ASDEX upgrade using doppler reflectometry, Plasma Phys.
Control. Fusion 47 (2005), pp. 1165–1186.
[22] H. Park, C.C. Chang, B.H. Deng, C.W. Domier, A.J.H. Donné, K. Kawahata, C. Liang, X.P. Liang, H.J. Lu,
N.C. Luhmann, Jr, et al., Recent advancements in microwave imaging plasma diagnostics, Rev. Sci. Instrum. 74
(2003), pp. 4239–4262.

116 A. Mase et al.

[23] S. Yamaguchi, Y. Nagayama, Z. Shi, R. Pavlichenko, S. Inagaki, Y. Kogi, and A. Mase, Microwave imaging
reflectometry in LHD, Plasma Fusion Res. 2 (2007), S1038.
[24] A. Mase, Y. Yokota, K. Uchida, Y. Kogi, N. Ito, T. Tokuzawa, K. Kawahata, K. Tanaka, Y. Nagayama, and H. Hojo,
Remote experiment of ultrashort-pulse reflectometry on LHD, Rev. Sci. Instrum. 77 (2006), 10E916.
[25] Y. Yokota, A. Mase, Y. Kogi, L. Bruskin, T. Tokuzawa, and K. Kawahata, Measurement of edge density pro-
files of large helical device plasmas using an ultrashort-pulse reflectometer, Rev. Sci. Instrum. 79 (2008),
056106.

Microwave advancement

More Related Content

Microwave advancement