Newton raphson method
- 1. NEWTON-RAPHSON METHOD Contents: Introduction Algorithm Flowchart Advantages & Disadvantages Example Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi 1
- 2. Introduction The Newton-Raphson technique, converges equally fast for large as well as small systems. Most widely used for solving simultaneous non-linear algebraic equations. It is a successive approximation procedure based on an initial estimate of the unknown and the use of Taylor’s series expansion 2 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
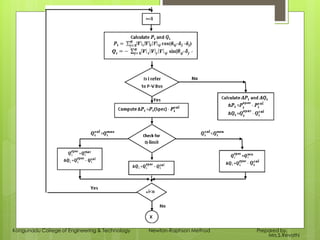
- 3. Algorithm Formulate 𝑌𝑏𝑢𝑠 matrix Assume flat start for starting voltage solution 𝛿𝑖 0 = 0, for i=1,2,3 …..N for all buses except slack bus 𝑉𝑖 0 = 1.0 for i=M+1, M+2, ……N(for all PQ buses) 𝑉𝑖 = 𝑉𝑖 𝑠𝑝𝑒𝑐 for all PV buses and slack bus. For load buses calculate 𝑃𝑖 𝑐𝑎𝑙 and 𝑄𝑖 𝑐𝑎𝑙 . For PV buses, check for Q-limit violation. If 𝑄𝑖(𝑚𝑖𝑛) <𝑄𝑖 𝑐𝑎𝑙 <𝑄𝑖(max), the bus acts as P-V bus. If 𝑄𝑖 𝑐𝑎𝑙 > 𝑄𝑖(max) 𝑄𝑖(spec) = 𝑄𝑖(max) If 𝑄𝑖 𝑐𝑎𝑙 <𝑄𝑖(𝑚𝑖𝑛) 𝑄𝑖(spec) = 𝑄𝑖(max), the P-V bus will act as PQ bus. Compute mismatch vector using, ∆𝑃𝑖 = 𝑃𝑖(𝑠𝑝𝑒𝑐) - 𝑃𝑖 𝑐𝑎𝑙 ∆𝑄𝑖 =𝑄𝑖(𝑠𝑝𝑒𝑐) - 𝑄𝑖 𝑐𝑎𝑙 3 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
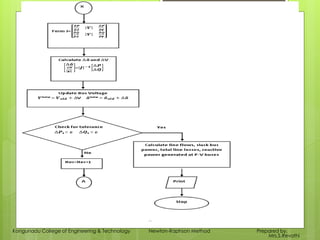
- 4. Contd… Compute, ∆𝑃𝑖(max) = max ∆𝑃𝑖 ; i=1,2,3 …..N’ ∆𝑄𝑖(max) = max ∆𝑄𝑖 ; i=M+1, M+2, ……N Compute Jacobian matrix using Form J= 𝜕𝑃 𝜕𝛿 𝑉 𝜕𝑃 𝜕𝑉 𝜕𝑄 𝜕𝛿 𝑉 𝜕𝑄 𝜕𝑉 Obtain state vector ∆𝛿 ∆V 𝑉 = 𝐽 −1 ∆𝑃 ∆𝑄 Update state vector using, 𝑉 𝑛𝑒𝑤 = 𝑉𝑜𝑙𝑑 + ∆V =𝑉𝑜𝑙𝑑 1 + ∆V 𝑉 𝑜𝑙𝑑 𝛿 𝑛𝑒𝑤 = 𝛿 𝑜𝑙𝑑 + ∆𝛿 This procedure is continued until, ∆𝑃𝑖 < 𝜀 ∆𝑄𝑖 < 𝜀, otherwise go to step 3. 4 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 5. Flowchart 5 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 6. 6 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 7. 7 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 8. Example… 1.Perform an iteration of Newton-Raphson load flow method and determine the power flow solution for the given system take base MVA as 100.(15) Line Bus Rp.u Xp.u Half line charging admittance Yp/2(p.u) Bus PL QL From To 1 90 20 1 1 1 0.0839 0.5183 0.0636 2 30 10 Step 1: Form 𝒀 𝒃𝒖𝒔 matrix 𝒀 𝒃𝒖𝒔 = 𝟏. 𝟖𝟒𝟐 −𝟏. 𝟒𝟎𝟓 𝟏. 𝟗𝟎𝟒 𝟏. 𝟕𝟑𝟏𝟒 𝟏. 𝟗𝟎𝟒 𝟏. 𝟕𝟑𝟏𝟒 𝟏. 𝟖𝟒𝟐 −𝟏. 𝟒𝟎𝟓 Step 2: Assume the initial value, 𝜹 = 0 V=1.0 𝑿 = 𝜹 𝟐 𝑽 𝟐 = 𝟎 𝟏. 𝟎 Step 3: calculate 𝑷 𝟐 𝒄𝒂𝒍 𝑸 𝟐 𝒄𝒂𝒍 and ∆𝑷 𝟐 and ∆𝑸 𝟐 𝑷 𝟐 𝒄𝒂𝒍 = 𝑉 2 𝑉 1 𝑌 12 cos(𝜃12 +𝛿2 -𝛿1) + 𝑉 2 𝑉 2 𝑌 22 cos(𝜃22 +𝛿2 -𝛿2) = -0.015 p.u 𝑸 𝟐 𝒄𝒂𝒍 = - 𝑉 2 𝑉 1 𝑌 12 sin(𝜃12 +𝛿2 -𝛿1) - 𝑉 2 𝑉 2 𝑌 22 sin(𝜃22 +𝛿2 -𝛿2) = -0.157 p.u ∆𝑃2 = 𝑃2(𝑠𝑝𝑒𝑐 ) - 𝑃2 𝑐𝑎𝑙 = -0.285 ∆𝑄2 =𝑄2(𝑠𝑝𝑒𝑐 ) - 𝑄2 𝑐𝑎𝑙 = 0.057 Step 4: Form Jacobian matrix 𝝏𝑷 𝟐 ∆𝛿2 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 𝝏𝑸 𝟐 𝜕𝛿 2 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 ∆𝛿2 ∆ 𝑉 2 𝑉2 = ∆𝑷 𝟐 ∆𝑸 𝟐 8 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 9. 𝝏𝑷 𝟐 ∆𝛿2 = 𝑉 2 𝑉 1 𝑌 12 sin(𝜃12 +𝛿2 -𝛿1) = 1.973 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 = 𝑉 2 𝑉 1 𝑌 12 cos(𝜃12 +𝛿1 -𝛿2) +2 𝑉 2 𝑉 2 𝑌 22 cos(𝜃22 ) =0.289 𝝏𝑸 𝟐 𝜕𝛿 2 = 𝑉 2 𝑉 1 𝑌 12 cos(𝜃12 +𝛿1 -𝛿2) = - 0.3197 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 = 𝑉 2 𝑉 1 𝑌 12 sin(𝜃12 +𝛿1 -𝛿2) +2 𝑉 2 𝑉 2 𝑌 22 sin(𝜃22 ) = 1.66 Step 5: Compute ∆𝑥, ∆𝛿2 ∆ 𝑉 2 𝑉2 = 𝝏𝑷 𝟐 ∆𝛿2 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 𝝏𝑸 𝟐 𝜕𝛿 2 𝑉 2 𝝏𝑷 𝟐 𝝏𝑽 𝟐 −1 ∆𝑷 𝟐 ∆𝑸 𝟐 = 1.973 0.289 −0.3196 1.66 −1 −0.285 0.057 = −0.145 0.064 𝛿2 1 = 𝛿2 0 +∆𝛿2 = - 0.145rad 𝑉2 1 = 𝑽 𝟐 + ∆ 𝑉 2 𝑉2 = 1.0064p.u 9 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 10. Advantages and disadvantages of N-R method. Advantages: The N-R method is faster, more reliable and the results are accurate. Requires less number of iterations for convergence The number of iterations are independent of the size of the system Suitable for large system Disadvantages The programming logic is more Memory requirement is more Number of calculations per iteration are high 10 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi
- 11. Conclusion: The Newton-Raphson method is explained with algorithm, flowchart and with an example. References: 1. Hadi Saadat, ‘Power System Analysis’, Tata McGraw Hill Education Pvt. Ltd., New Delhi, 21st reprint, 2010. 2. Kundur P., ‘Power System Stability and Control, Tata McGraw Hill Education Pvt. Ltd., New Delhi, 10th reprint, 2010. 3. Pai M A, ‘Computer Techniques in Power System Analysis’, Tata Mc Graw-Hill Publishing Company Ltd., New Delhi, Second Edition, 2007. 4. J. Duncan Glover, Mulukutla S. Sarma, Thomas J. Overbye, ‘ Power System Analysis & Design’, Cengage Learning, Fifth Edition, 2012. 5. Olle. I. Elgerd, ‘Electric Energy Systems Theory – An Introduction’, Tata McGraw Hill Publishing Company Limited, New Delhi, Second Edition, 2012. 6. C.A.Gross, “Power System Analysis,” Wiley India, 2011. 7. M.Jeraldin Ahila “Power System Analysis”, Lakshmi Publications, Chennai, Eleventh Edition 2017. 8. Web Sources 11 Kongunadu College of Engineering & Technology Newton-Raphson Method Prepared by, Mrs.S.Revathi