Optimization

“OPTIMIZATION TECHNIQUES
IN PHARMACEUTICAL
FORMULATION”
Presented by
MAHESH A. KESALKAR
{Pharmaceutics}
Institute of Pharmaceutical Education And
Research, Borgaon (Meghe), Wardha
1

CONTENTS
2
Introduction
Optimization parameter
Classic optimization
Optimization methods
Applications

INTRODUCTION
3
•The term Optimize is defined as to make perfect , effective , or
functional as possible.
•It is the process of finding the best way of using the existing
resources while taking in to the account of all the factors that
influences decisions in any experiment
•Traditionally, optimization in pharmaceuticals refers to changing
one variable at a time, so to obtain solution of a problematic
formulation.
•Modern pharmaceutical optimization involves systematic design of
experiments (DoE) to improve formulation irregularities.
•In the other word we can say that – quantitate a formulation that
has been qualitatively determined.
•It’s not a screening techniques

4
Why optimization is Necessary ?

5
TERMS USED :
FACTOR: It is an assigned variable such as concentration ,
Temperature etc..,
Quantitative: Numerical factor assigned to it
Ex; Concentration- 1%, 2%,3% etc..
Qualitative: Which are not numerical
Ex; Polymer grade, humidity condition etc
LEVELS: Levels of a factor are the values or designations
assigned to the factor
FACTOR LEVELS
Temperature 300 , 500
Concentration 1%, 2%

6
RESPONSE: It is an outcome of the experiment.
It is the effect to evaluate.
Ex: Disintegration time etc..,
EFFECT: It is the change in response caused by varying the
levels
It gives the relationship between various factors & levels
INTERACTION: It gives the overall effect of two or more
Variables
Ex: Combined effect of lubricant and glidant on hardness of the
tablet

OPTIMIZATION PARAMETER
1. Problem types
a. Constrained
b. Unconstrained
2. Variable types
a. Dependent
b. Independent
i. Formulating variable
ii. Processing variable

Optimization Parameters
1.Problem types:
Constraints
Eg. Making hardest tablet but should disintegrate within 20 mins
Unconstraint
Example: Making hardest tablet
•2. Variables:
Independent variable-
E.g. - mixing time for a given process step.
granulating time.

9
Dependent variables
which are the responses or the characteristics of the in material
Eg. Particle size of vesicles, hardness of the
tablet.
Higher the number of variables, more complicated will be the
optimization process.
There should be a relationship between the given response and the
independent variable, and once this relationship is established , a response
surface is generated.
From response surface only, we find the points which will give
desirable value of the response.

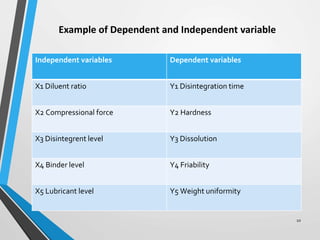
10
Example of Dependent and Independent variable
Independent variables Dependent variables
X1 Diluent ratio Y1 Disintegration time
X2 Compressional force Y2 Hardness
X3 Disintegrent level Y3 Dissolution
X4 Binder level Y4 Friability
X5 Lubricant level Y5 Weight uniformity

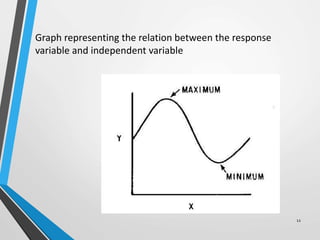
CLASSICAL OPTIMIZATION
•Classical optimization is done by using the calculus to basic
problem to find the maximum and the minimum of a
function.
•The curve in the fig represents the relationship between the
response Y and the single independent variable X and we can
obtain the maximum and the minimum. By using the calculus
the graphical represented can be avoided. If the relationship,
the equation for Y as a function of X, is available [Eq]
Y = f(X)

12
Graph representing the relation between the response
variable and independent variable

When the relation for the response y is given as the function of
two independent variables,x1 &X2
Y = f(X1 , X2)
The above function is represented by contour plots on which
the axes represents the independent variables x1& x2

OPTIMIZATION METHODS
14
Optimization methods
1) Evolutionary operation
2) Simplex method
3) Lagrangian method
4) Search method
5) Canonical analysis

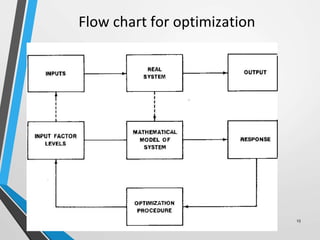
Flow chart for optimization
15

16
• It is a method of experimental optimization.
• Small changes in the formulation or process are made
(i.e. repeats the experiment so many times) & statistically
analyzed whether it is improved.
• It continues until no further changes takes place i.e., it
has reached optimum-the peak.
• The result of changes are statistically analyzed.
1) Evolutionary Operations

• It is an experimental techniques & mostly used in analytical rather
than formulation & processing.
Simplex is a geometric figure that has one more point than the
number of factors.
e.g -If 2 independent variables then simplex is represented as
triangle.
•The strategy is to move towards a better response by moving away
from worst response.
•Applied to optimize CAPSULES, DIRECT COMPRESSION TABLET, liquid
systems (physical stability).
•It is also called as Downhill Simplex / Nelder-Mead Method.
17
2) Simplex Method(Simplex Lattice)

18
A simplex lattice of four component is shown by
15 formulation
4 formulations of each component A,B,C&D
6 formulation of 50-50 mixture of AB, AC, AD, BC, BD&CD.
4 formulation of 1/3 mixtures of three components
ABC, ABD, ACD, & BCD.
1 formulation of 25% of each of four
Component
(ABCD)

19
•It represents mathematical techniques & it is applied to a
pharmaceutical formulation and processing.
•This technique follows the second type of statistical design
Disadvantage-Limited to 2 variables
•Helps in finding the maxima (greatest possible amount) and
minima (lowest possible concentration) depending on
the constraints.
•A techniques called “sensitivity analysis“ can provide
information so that the formulator can further trade off one
property for another . Analysis for solves the constrained
optimization problems.
3) Lagrangian method

Steps Involved
• Determine objective formulation
• Determine constraints.
• Change inequality constraints to equality constraints.
• Form the Lagrange function F:
• Partially differentiate the lagrange function for each variable &
set derivatives equal to zero.
• Solve the set of simultaneous equations.
• Substitute the resulting values in objective functions.

21
4)Search methods (RSM) :
•It takes five independent variables into account and is
computer-assisted.
•It is defined by appropriate equations.
•Response surface methodology is used to determine the
connection between different explanatory variables
(independent variables) and one or more of the response
variables.
•Persons unfamiliar with mathematics of optimization & with
no previous computer experience could carryout an
optimization study.

1. Select a system
2. Select variables:
a. Independent
b .Dependent
3. Perform experimens and test product.
4. Submit data for statistical and regression analysis
5. Set specifications for feasibility program
6. Select constraints for grid search
7. Evaluate grid search printout
8. Request and evaluate
a. “Partial derivative” plots, single or composite
b. Contour plots
22
Search Methods

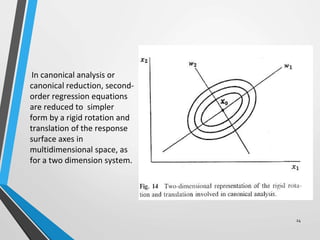
5) Canonical analysis
• It is a technique used to reduce a second order regression
equation.
• This allows immediate interpretation of the regression
equation by including the linear and interaction terms in
constant term
• It is used to reduce second order regression equation to an
equation consisting of a constant and squared terms as
follows-
Y = Y0 +λ W12+ λ2W22 +..
2variables=first order regression equation.
3variables/3level design=second order regression equation. 23
1

. In canonical analysis or
canonical reduction, second-
order regression equations
are reduced to simpler
form by a rigid rotation and
translation of the response
surface axes in
multidimensional space, as
for a two dimension system.
24

Forms of Optimization techniques:
1. Sequential optimization techniques
2. Simultaneous optimization techniques.
25

26
Sequential Methods:
Also referred as the "Hill climbing method".
initially small number of experiments are done, then research is done using
the increase or decrease of response.
Thus, maximum or minimum will be reached i.e. an optimum solution.
Simultaneous Methods:
Involves the use of full range of experiments by an experimental design.
Results are then used to fit in the mathematical model.
Maximum or minimum response will then be found through this fitted model

Reference
29
o Modern pharmaceutics, by Gillbert and S. Banker

Optimization

More Related Content

Optimization