PRML 5.3-5.4
- 1. PRML勉強会 5.3,5.4 坪坂正志(mail: m.tsubosaka@gmail.com) 1 第6回PRML読書会 2009/8/29
- 2. 発表内容 誤差逆伝播 (5.3) 誤差関数の勾配を効率よく計算するテクニック 誤差関数だけではなく、他の微分の計算にも応用可能 最適化アルゴリズム 最急降下法 逐次的最急降下 慣性項(momentum)の導入 準Newton法 BFGS公式 ヘッセ行列(5.4)(#数式を書く気力がなかったので黒板 で) 逆伝播を使って計算 2 第6回PRML読書会 2009/8/29
- 3. 参考資料 田村・村松:「工系数学講座 最適化法」, 共立出版 (2002) LeCun Y., Bottou L., Orr G.,and Miiller K. : Efficient BackProp, Neural Networks: Tricks of the trade(LNCS), Springer, 1998 3 第6回PRML読書会 2009/8/29
- 4. 5.3 誤差逆伝播 フィードフォワードニューラルネットワークにおいて、誤差 関数 の勾配を評価 順向き伝播(forward propagation)と逆伝播 (backpropagation)を用いた局所的なメッセージパッシ ングスキームを用いて実現できる ネットワークの重みに比例した時間で計算可能 4 第6回PRML読書会 2009/8/29
- 5. 5.3 誤差逆伝播 逆伝播によって勾配を求めるステージとネットワークの 重みを調整(学習)するステージは別々 1. 逆伝播によって勾配を求める 2. 勾配降下法などの最適化スキームを用いて重みを調整 たとえばヘッセ行列を計算すればNewton法を用いること ができる。また、勾配が分かれば準ニュートン法(BFGS 法)が適応できる。 5 第6回PRML読書会 2009/8/29
- 6. 5.3.1 誤差関数微分の評価 各データに対応する誤差項の和の形で表される誤差関 数を考える: (5.44) 1つの項に対応する勾配 を評価すれば より誤差関数の勾配も計算できる。 6 第6回PRML読書会 2009/8/29
- 7. 線形モデルの場合 出力 が入力変数 を線形和 (5.45) の形で書け、誤差関数が (5.46) と表されるとする。 このとき重み に関する勾配は となる。 誤差信号 リンクの入力 7 第6回PRML読書会 2009/8/29
- 8. 線形モデルのイメージ 入力 出力 隠れ層がないニューラルネットワークに相当 勾配の計算 ① 入力から出力を計算 ② 出力と目的値の誤差信号を計算 ③ 誤差信号から重みに関する微分を計算 重みに関する微分 = (出力側のユニットの誤差)×(入力側のユニットの値) 8 第6回PRML読書会 2009/8/29
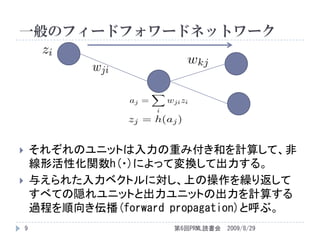
- 9. 一般のフィードフォワードネットワーク それぞれのユニットは入力の重み付き和を計算して、非 線形活性化関数h(・)によって変換して出力する。 与えられた入力ベクトルに対し、上の操作を繰り返して すべての隠れユニットと出力ユニットの出力を計算する 過程を順向き伝播(forward propagation)と呼ぶ。 9 第6回PRML読書会 2009/8/29
- 10. 微分の評価 の に関する微分の評価は がユニット へ の入力和 を通してのみ に依存することに着目 するとChain ruleにより (5.50) のように分解できる。(簡単のため変数からnは省略する) 誤差(5.51) (5.52) を使うと(5.50)の式は線形モデルと同じ形をとる (5.53) 10 第6回PRML読書会 2009/8/29
- 11. 誤差の評価(1/2) 出力ユニットでは誤差の値は (5.54) となる。(活性化関数に正準連結関数を用いた場合) 隠れユニットでの誤差の値はChain ruleより (5.55) となる。 はユニット から接続されているすべてのユニッ トの添え字である 11 第6回PRML読書会 2009/8/29
- 12. 誤差の評価(2/2) 上の式より(5.55)は (5.56) となる。この式を逆伝播公式という。 誤差の評価を出力ユニットから再帰的に計算すれば全 ての隠れユニットの誤差が計算できる。 12 第6回PRML読書会 2009/8/29
- 13. 誤差逆伝播アルゴリズム 1. 入力ベクトル をネットワークに入れ、順向き伝播に よってすべての隠れユニットと出力ユニットの出力を評 価する 2. すべての出力ユニットの誤差を評価する 3. 接続先のユニットの誤差の評価が終わっている隠れユ ニットに対して逆伝播公式を用いて再帰的に誤差を評 価する 4. 式 を用いて必要な微分を評価する 13 第6回PRML読書会 2009/8/29
- 14. 5.3.3 逆伝播の効率 誤差逆伝播の計算量は全体で ここで はネットワークの重みとバイアスの総数 たとえば2層ネットワークならば M * (D + K) 順伝播での評価に 逆伝播での(5.54)と(5.56)の評価も 微分の評価が ( : ユニットの数) 14 第6回PRML読書会 2009/8/29
- 15. 数値微分を用いた場合の効率 微分を十分小さい を用いて と近似する。 この近似を使って評価する場合、 個のすべての重み に対して順向き伝播を適応する必要があり全体の計算 量は となる。 計算量を考えると数値微分を用いる意味はないが、逆 伝播アルゴリズムのソフトウェアの実装の正しさをチェッ クするツールとなる。 15 第6回PRML読書会 2009/8/29
- 16. 中心差分を用いた近似(演習5.14) より 成立する。 16 第6回PRML読書会 2009/8/29
- 17. 5.3.2 単純な例 2層ネットワークの例を考える 誤差関数:2乗和 隠れユニット:シグモイド活性化関数 出力ユニット:線形活性化関数 17 第6回PRML読書会 2009/8/29
- 18. シグモイド活性化関数 隠れユニットの活性化関数には を用いる この関数の特性として (5.60) となる性質がある。 18 第6回PRML読書会 2009/8/29
- 19. 順向き伝播 以下の式を用いて順向き伝播を実行する (5.62) (5.63) (5.64) 19 第6回PRML読書会 2009/8/29
- 20. 逆伝播 出力ユニットでの の値は を使って計算できる。 隠れユニットでの の値は逆伝播公式より で計算できる。 重みに関する微分: 20 第6回PRML読書会 2009/8/29
- 21. バイアスについて 発表中には混乱したのですがバイアスユニットの は計 算する必要はないです 各リンクの重みに関する勾配は で入力が入っ てくる部分のユニットの しか計算に影響しないので、入 力に依存しないバイアスユニットの項に関しては計算す る必要がない。 21 第6回PRML読書会 2009/8/29
- 22. 5.3.4 ヤコビ行列 逆伝播アルゴリズムは重みに関する微分だけではなく、 他の微分計算にも応用可能 例えばヤコビ行列の評価に用いることができる ヤコビ行列の各要素は出力の入力に関する微分で与えられ る 入力変数の変化に対する出力の感度の指標となっている 22 第6回PRML読書会 2009/8/29
- 23. モジュール型パターン認識システム 誤差関数 をパラメータ に対して微分した値は右側中 央のモジュールのヤコビ行列が分かれば計算できる。 23 第6回PRML読書会 2009/8/29
- 24. 逆伝播手続きの導出(1/2) ヤコビ行列の要素 は となる(ここで和は入力ユニット が結合をもつすべてのユ ニット に関してとる) これからヤコビ行列の評価には を評価すればよい ことが分かる。 24 第6回PRML読書会 2009/8/29
- 25. 逆伝播手続きの導出(2/2) の値は とユニット から接続されているユニット の入力の微分 を用いて再帰的に記述できる。 25 第6回PRML読書会 2009/8/29
- 26. 出力ユニットにおける微分 出力ユニット における微分の値は活性化関数の関数 形式を直接微分することにより求められる。 線形活性化関数 はクロネッカーのデルタ シグモイド活性化関数 ソフトマックス関数 26 第6回PRML読書会 2009/8/29
- 27. 5.3 まとめ 誤差逆伝播を用いて勾配情報を効率的に計算する方法 について述べた。 逆伝播のテクニックを用いるとヤコビ行列などの評価も 可能になる。 27 第6回PRML読書会 2009/8/29
- 28. 最適化手法について 誤差逆伝播によって勾配が与えられたときにどうやって ネットワークの重みを更新するか? 最も単純な方法としては のように更新する方法である ここで は学習率パラメータとして知られている この方法では性能が悪い 学習率を大きくすると数値が発散したりする 小さいと収束が非常に遅くなる 28 第6回PRML読書会 2009/8/29
- 29. 直線探索(line search) 学習率パラメータ の決め方に関して 最急降下以外デモに関数 の最小化/最大化を行う 際に の形の更新を繰り返す最適化手法が多い。 このとき を探索方向と呼び、 を決定することを直 線探索と呼ぶ の決定方法としては が適当な基準を満たすまで小 さくしていくという方法をとることが多い(Backtracking line search) 29 第6回PRML読書会 2009/8/29
- 30. 直線探索の基準について アルミホの基準(Armijo’s rule) ウルフの基準(Wolfe’s rule) アルミホの基準 + 下の式が成立 30 第6回PRML読書会 2009/8/29
- 31. 逐次的勾配降下法 重みの更新を一回ごとに一つのデータ点に基づいて作 成する。 このような各点で行う手法をオンライン手法といい、デー タをすべて用いる方法をバッチ手法と呼ぶ データをmini-batchと呼ばれる小さい部分に分割して学 習を行う場合もある。 31 第6回PRML読書会 2009/8/29
- 32. オンライン vs バッチ オンライン バッチ処理に比べて大規模データが扱いやすい データが加わった時や変化した際に学習が容易 バッチ 収束条件が明確 共役勾配法などの手法を用いやすい 理論的解析や収束速度が扱いやすい 32 第6回PRML読書会 2009/8/29
- 33. 慣性項(momentum)を用いる方法 学習規則を以下のように表す 最急降下では となる。 慣性項 を用いて と更新すると収束を加速できる(何で加速になっているか はまだよくわかってない)。 33 第6回PRML読書会 2009/8/29
- 34. 準ニュートン法 準ニュートン法は関数 を最小化する手法の一つ 制約なし非線形最適化の中で非常にオーソドックスな方 法 ベクトル を以下の更新式で更新する ここでベクトルの更新後に を更新する 34 第6回PRML読書会 2009/8/29
- 35. 他手法との関係 : 最急降下法 (ヘッセ行列): ニュートン法 準ニュートン法の由来としては がヘッセ行列の近 似となっていることから来ている 35 第6回PRML読書会 2009/8/29
- 36. BFGS(Broyden–Fletcher–Goldfarb–Shanno)公式 以下のように変数を定義する を以下の公式(BFGS公式)で更新 を適切に選択したうえで適切な仮定の下で超一次収 束 36 第6回PRML読書会 2009/8/29
- 37. 収束速度について 点列 が に収束しているとする 一次収束 超一次(super linear)収束 二次収束 37 第6回PRML読書会 2009/8/29
- 38. L-BFGS BFGS法ではパラメータ数がnのときO(n^2)の空間計算量 がかかる 行列の値ではなく反復推定時の過去m回のベクトルの更 新履歴のみを覚えておくのがL-BFGS法。 この場合O(mn)の空間計算量で通常反復は10回程度で 終わるので問題ない Software libLBGFS (C++): http://www.chokkan.org/software/liblbfgs/ L1正則化項(微分不可)を用いた関数の最適化にも対応 38 第6回PRML読書会 2009/8/29
- 39. 5.4 ヘッセ行列 すべての重みパラメータとバイアスパラメータを1つのベ クトル の要素 とする。 このとき、誤差の二階微分 はヘッセ行列の成分 をなす。 個のパラメータがあるときにはヘッセ行列の要素は 個存在し、計算量としては は必ず必要で、また 実際に で計算する手法が存在する(PRML 5.4.5, Bishop 1991; Bishop,1992) 39 第6回PRML読書会 2009/8/29
- 40. ヘッセ行列を用いるメリット ヘッセ行列を計算することにより、以下のような用途に用 いることができる 1. 非線形最適化アルゴリズムに利用(cf. Newton法) 2. 訓練データが尐しだけ変わった場合に高速に再学習を行う ために使う(Bishop,1991) 3. 「刈り込み」アルゴリズムの一部として不要な重みを特定す るのに用いられる(Le Cun et al.,1990) 4. ベイズニューラルネットワークのラプラス近似の際に中心的 な役割を果たす 40 第6回PRML読書会 2009/8/29
- 41. ヘッセ行列の計算手法 近似計算 対角近似(5.4.1) O(W)で計算可能 外積による近似(5.4.2) O(W^2)で計算可能 効率的に逆行列が計算できる(5.4.3) 差分近似(5.4.4) ナイーブにやるとO(W^3)がかかるが、逆伝播を用いて1階微分を用 いるとO(W^2)で計算可能 厳密評価(5.4.5) 41 第6回PRML読書会 2009/8/29
- 42. 対角近似(5.4.1) ヘッセ行列の応用上で逆行列が必要になることが多い がヘッセ行列が対角であれば容易に求めることができる 近似式の評価がO(W)で計算できる。 Becker and Le Cun 1989; Le Cun et al.,1990 Ricotti et al.(1998)では対角項に関して正確な値を得て いるが代わりにO(W^2)の計算量がかかる 問題として実際のヘッセ行列が極端な非対角であること が多いため注意が必要 42 第6回PRML読書会 2009/8/29
- 43. 式(5.79)導出補足 43 第6回PRML読書会 2009/8/29
- 44. 外積による近似(5.4.2) 誤差関数が の形のときにヘッセ行列は で出力が目標値に十分近いとき第2項を無視できるため と近似できる(Levenberg-Marquardt近似) 44 第6回PRML読書会 2009/8/29
- 45. ヘッセ行列の逆行列(5.4.3) 外積による近似を用いると逆行列の近似するための計 算上効率的な手続きを導出できる(Hassibi and Stork, 1993) 最初のL個のデータ点を用いて作成されたヘッセ行列を とすると の逆行列は の逆行列から効率的に導出できる。 初めの行列を とすると の逆行列を見つけ ることになる( ) 45 第6回PRML読書会 2009/8/29
- 46. 有限幅の差分による近似(5.4.4) ヘッセ行列の各項は を計算すればよく、 が誤差逆伝播で効率的に求まるこ とから で計算できる 46 第6回PRML読書会 2009/8/29
- 47. ヘッセ行列の厳密な評価(5.4.5) O(W^2)で効率的に評価する方法が存在する(Bishop 1991; Bishop 1992) Buntine and Weigend(1993)でも類似の方法が考察さ れている 2層ネットワークの場合は必要な式は容易?に導かれる それぞれの重みが第何層にあるかで場合分けを行う (5.93),(5.94),(5.95) 47 第6回PRML読書会 2009/8/29
- 48. ヘッセ行列の積の高速な計算(5.4.6) ヘッセ行列 自体ではなく、あるベクトル との積が必 要であることが多い。 このときヘッセ行列を評価して、積を求めるとO(W^2)の 時間/空間計算量が必要である しかし、誤差逆伝播の手順を利用することによってO(W) で効率的に計算するアルゴリズムが存在する。 (Pearmutter 1994) 48 第6回PRML読書会 2009/8/29
- 49. 計算方法のアウトライン 計算したい値: は誤差逆伝播で求まる 誤差逆伝播を求めるすべての方程式に微分演算子 を作用させる 49 第6回PRML読書会 2009/8/29
- 50. ちなみに5章とは関係ないですが 今日ここまでの話+いままでのPRMLを聞いておくと、以下 の論文は読めると思います R. Salakhutdinov and A. Mnih: Probabilistic Matrix Factorization , NIPS 20, 2008 最近の協調フィルタリングで用いられている基本的手法 の一つ 単純な類似度ベースの方法より速度、精度ともに上 必要知識 最急降下法(慣性項含む) ロジスティック関数の微分 ガウス分布 (グラフィカルモデル PRML 8章) 50 第6回PRML読書会 2009/8/29