Q01222110120

IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE)
e-ISSN: 2278-1684,p-ISSN: 2320-334X, Volume 12, Issue 2 Ver. II (Mar - Apr. 2015), PP 110-120
www.iosrjournals.org
DOI: 10.9790/1684-1222110120 www.iosrjournals.org 110 | Page
A Analytical Model For Vibration Period With SSI Of R/C
Structures
Turkia Haithem1
, Lahbari Noureddine²
1,2,
Department of Civil Engineering, Institute of Civil Engineering, Hydraulique and Architecture, University of
Batna,Algeria
Abstract: The effect of the fundamental period, the soil structure interaction SSI, and the site on the seismic
behaviour of R/C structures is investigated using analytical model based on the Algerian seismic regulations.
Hence the aim of this study is to formulate model covering the fundamental period of vibrations based on a
system with continuous columns in which the deformations of structure and soil represent the degree of
freedom. Shear and flexural deformation are appointed for the structure, whereas relative displacement of the
foundation base and rocking are meant for the soil( isolated footings for stiff and medium soil - sites S1, S2 and
mat for soft soil sites S3 or S4).Finite element method is used to analyse the response of various R/C frames (low,
medium and high rise),assuming fixed and flexible base,(vertical, horizontal translations stiffness, rocking and
torsional stiffness),and compared with Newmark Rosenblueth, Deleuze and Gazetas methods.
Keywords: soil structure interaction, foundation, R / C frame, Seismic response, effective periods.
I. Introduction
Often, seismic structural design is based on rigid base assumption, and interaction with the soil-
foundation system is either ignored or carried out separately, whereas in reality these systems are coupled.
Ignoring the SSI effects may lead to erroneous structural assessment and estimates of seismic demands.
This work presents a simplified and accurate formulation using finite element method applied to the
analytical model based on the Algerian seismic regulation, a rapid assessment of the fundamental period of
vibrations when SSI effects are accounted for. Furthermore, it investigates the importance of SSI phenomena on
the response of frames as function of different parameters such as soil rigidity, foundation rigidity, foundation
mass, and soil mass.
It is shown that for structures founded on soft soils with high relative rigidity, the SSI effects amplifies
the dynamic response of the system. Also, it is not necessary to take into account SSI effects when designing a
R/C building on stiff soil.
II. Formulation Of The Soil Structure Interaction - Description Of Model SSI
Based on the formules of the period of vibration given by THOMPSON [1] neglecting SSI effects, the
new formulation taking into account SSI effects will be as follows:
2.1 Shear Mode with SSI (T*
S)
In this case the bending deformation is negligible and the shear deformation is the determining factor in
calculating the period. The fundamental period of vibration in Shear mode is given by:
Where:
Ts: Shear fundamental period without SSI is given by [2]:
W*: Total mass calculated from structure, soil and foundation; WSt: Total mass calculated from structure; r:
Ratio of shear stiffness equal to: RS/R*
S
R*
S, RS: Shear stiffness with and without SSI.
)1()()(T 2*2**
bs TT 
)2(*
**
mr
R
R
W
W
T
T
S
S
Sts
s

)4(*
*
S
S
S
S
F
AG
Rand
F
AG
R 
)3(4
1
444
2
S
St
S
St
SS
S
gR
HW
RHg
W
H
R
H
AG
F
HT 




A analytical model for vibration period with SSI of R/C structures
A: area of the section; G: Modulus of the reinforced concrete; FS, F*
S: security coefficient without and with SSI.
m: Ratio of unit mass of building is given by:
Where:
WF: foundation mass ;WS: soil mass.
2.2 flexural Mode with SSI
In this case the shear deformation is negligible and the bending is the determining factor in calculating the
period.
Tb: Flexural fundamental period without SSI is given by [2]:
I*
: Total moment of inertia of the structure with SSI.
Consequently:
: Ratio of the moment of inertia with and without SSI given by:
Where:
IF : Moment of inertia of the foundation.
ISt : Moment of inertia calculated of the structure only without SSI.
2.3 Rocking mode
2.3.1 The case of isolated footings (stiff and medium soil - site S1, S2)
Using the simplified method from VELETSOS [3,4,5], the expression of rocking stiffness K from vertical and
rocking stiffnesses of the soil is:
With:
K vi and Ki the corresponding vertical and rocking stiffnesses respectively.
Yi represents the normal distance from the centroid of the ith
footing to the rocking axis of the foundation.
The vertical and rocking stiffnesses of the ith
footing are defined by the following relations [3]:
With rai and rmi are given as follows [3, 6]
r ai: Radius of a circular footing that has the area of the ith
footing; d i: Depth of effective embedment for the ith
footing.
)6(79.179.1
2
*
*
*
*
2
*
*
gEI
HW
H
EI
HT
b
b 



)8(*
**
m
I
I
W
W
T
T
b
b

)5(1
*
St
S
St
F
St
SFSt
St W
W
W
W
W
WWW
W
W
m 


)9(1
1 *
St
F
St
FSt
St I
I
I
II
I
I




)7(79.179.1
2 2
St
St
Stb
b
gEI
HW
H
EI
HT 



  )10(2
ivii yKKK 
)12(21
)1(3
8
)11(
5
2
1
1
4
3


















mi
imii
i
ai
iai
vi
r
drG
K
r
dGr
K



)14(
4
)13(
4


F
mi
F
ai
I
r
A
r



2.3.2 The case of mat (soft soil - site S3, S4)
From the simplified method of VELETSOS [4,5] described by SOULUMIAC [7] and based on the text
of ATC-3 [8]; The expression of rocking stiffness K of rectangular footing can be expressed by [3]:
Where: K: Rocking stiffness of rectangular footing; G: Shear modulus of soil beneath the ith
footing; : The
Poisson's ratio of soil.
rm: Radius of the circle of the equivalent foundation calculated as follows:
With:
AF: Area of the section of the foundation.
Then:
The final formulation for the fundamental period of vibration, taking into account SSI effect will be:
III. Formulation Of SSI To Reinforced Concrete Frames
In the following, an approximate formula for the lateral drift of the frame is determined by considering
the interaction of soil structure. The assumptions of the method of analysis of rigid frame were adopted [9].
Figure 1 shows the frame after deflection under lateral forces. The total lateral displacement of a level U*
is
equal to the sum of the displacement without SSI and the displacement due to the interaction Ur [2, 10].
U*
= U+ UR (19)
Where:
U*
: The total lateral displacement with SSI; U: The displacement at the nth
floor of the built structure without
SSI.
U = UC + Ug (20)
UC, Ug: The displacement of the columns due to the bending mode and the displacement of the beams due to the
shear mode.
UR: The displacement due to the translation and rocking of the foundation [11, 12, 13].
The lateral displacement U without SSI is calculated by [2]:
The linear rigidities of columns and beams are:
V: shear force at the base of the structure without SSI.
Ic , Ig : moment of inertia of the columns and beams respectively
NC: Number of columns.
E: Modulus of elasticity of the concrete.
h: story height.
L: length of bay.
The total displacement taking into account the SSI is calculated by simplified method from VELETSOS [3] as:
Where:
V*
: The reduced shear force corresponding to the soil structure interaction (with SSI).
M0 : The moment due to the lateral forces without SSI is: (2HV)/3
)15(
)1(3
8 3


mGr
K
)16(

FF
m
IA
r 
)17(
)1(3
8 3

FAIG
K


)18(22*
bS TmmrTT 
)21(
)1(12
])1²[(
CgCC
CCgC
KKNEN
KNKNVh
U



)23(0
*
*








U
K
HM
V
V
U
)22(
L
I
Kand
h
I
K
g
g
C
C 

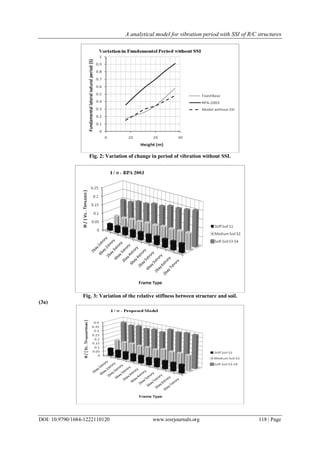
K: The rocking stiffness of the foundation with SSI.
H: total height of the structure.
Then the shear deformation due to the lateral displacement will be:
Where:
: The shear deformation without SSI calculated by:  = U / h
Hence the shear stiffness with SSI is:
The Shear stiffness without SSI [2] is:
And consequently the stiffness ratio r is:
 Is the stiffness corrector ratio with effects SSI
IV. Numerical Application
4.1 Characteristics of dimensionless parameters
The characteristic parameters of the interaction model are defined as well as the intervals of typical
values for building structures as follows [14]:
- Ratio of the foundation mass to the structure mass: 0 ≤ WF / WSt ≤ 0.5
- Ratio of the moment of inertia of the foundation to the mass moment of inertia of the structure: 0 ≤ IF / I Str
≤ 0.1
- Damping ratio for the fixed-base structure and the soil  = 0.07, which is a conventional value adopted for
the most buildings and soils (SSI effects are not sensitive to the. Fixed base structural damping ratio [23])
- Poisson's ratio for the soil: µ =0.20, 0.25 and 0.4 which are representative values for stiff, medium and soft
soils, respectively.
- Ratio of the shear stiffness: 1 ≤ r ≤ 1.1
- Relative mass density between the structure and the soil: 2 ≤ WS / WSt ≤ 5.
- Slenderness ratio of the structure: H / R = 2 to 5.
4.2 Assumptions
In the case of structures without SSI, the assumption of fixed base is used to estimate the fundamental
period of vibrations. This is assessed according to the RPA code [15] for different categories of sites. In the case
of structures with SSI, the soil is modelled by springs: horizontal, vertical and rocking.
To determine the stiffness, the methods of NEWMARK - ROSENBLUETH, DELEUZE and GAZETAS [16,
17] are applied. The shear modulus of the soil G is given three values, the density of soil is set at 2t/m3
and the
coefficient of critical damping is taken as  = 7%; Table. 1 summarizes the different values.
V. Results
- Table 2 presents values of fundamental natural periods calculated by different methods: exact method, RPA
code [15], ADELI model without soil-structure interaction.
- It shows a good correlation between exact solution and ADELI model [1] without SSI: a difference of 2.5%
is observed in all sites for the ratio Texact / TADELI with a deviation of 0.09, Fig. 2.
- It can be observed from the results that the interaction effects are negligible (1/ < 0.10) in stiff soil and
outstanding in medium and soft Soil (1/ > 0.10), Table 3 (Fig.3a).These results are in good correlation
with those obtained by MASSUMI, TABATABAIEFAR [18] and MICHAEL JAMES GIVENS [11].
- The incorporation of SSI and number of stories tends to increase the fundamental period by 26.3% in
medium soil S2 and 27.9% in soft soil S3 – S4 as showed in [19]
)24(
**
*









K
M
V
V
H
U O
)25(
23
3
*
*
*
S
SO
S R
HRK
K
K
M
VV
R
















)27(1
3
2
1
3
32
*






K
HR
K
KHR
R
R
r SS
S
S
)26(
])1[(
)1(12
CCgC
gcCC
s
KNKNh
KNKEN
R




- The effect of soil-structure interaction is to be considered when the following criterion is satisfied: H/ (Vs
.T) > 0.10.
- The values of factor 1/ for the seismic behaviour of R/C structures, according to the Algerian code
RPA2013 considering the SSI effect, are given only for soft soil site S3, (Fig.3b).
- Table 4 presents values of the natural periods with SSI obtained by the methods of NEWMARK -
ROSENBLUETH, DELEUZE and GAZETAS and by the proposed model.
- The fundamental periods of vibration obtained by the proposed model gives good results compared to
GAZETAS, DELEUZE and NEWMARK- ROSENBLUETH methods: 5.57% for site S2 and 6.01% for site
S3, (Fig.4).
VI. Discussions
- Influence of the ratio WF / WSt: the period of vibrations increase with the increase of the ratio WF/WSt
,about 7.4% in soft and medium soil.
- Influence of the ratio IF / ISt : no notification < 1% as showed by[35].
- Influence of the ratio WS / WSt : increase of the period with the increase of the mass soil about 27%
(Fig.5),[10] presents an increase of 20%
- Influence of the ratio D/R: no notification: > 2%.
- The variation of lateral natural period due to incorporation SSI increases with the reduction in stiffness of
soil. It is minimum in case of stiff soil (S1) and maximum in soft soil (S3 and S4) about 75%. A maximum
increase of more than about 78% is noted in [21] and 70% in [22]
VII. Conclusion
- When considering SSI effects, the soil flexibility and number of stories have an influence on the naturel
period.
- Natural period of R/C system including SSI effects increases when the ground is softer.
- It is not necessary to consider the effect of soil–structure interaction for seismic design of reinforced
concrete frame buildings founded on stiff soil. Hence it is possible to include the soil-structure interaction
effects in the analysis of multi-story building response by other means such as incorporating a few
modifications to the fixed base condition. These modifications include mass of soil, inertia of foundation,
ratio of shear stiffness and slenderness.
- As 1/ increases, the significance of SSI effects increases.
- Finally, it is essential to consider the effect of soil-structure interactions for seismic design of reinforced
concrete frame for: 1/ > 0.10
References
[1]. Thompson W.T, theory of vibration with application, 2nd edition, Prentice Hall,Englewood cliffs, New jersey,(1981).
[2]. Adeli H, Approximate formulae for period of vibrations of building systems, civil engineering for practising and design engineers,
Vol4 Nb1 pp93-128, junnary 1985.
[3]. Victor.D , la construction en zone sismique, Paris, Editions le Moniteur 1999.
[4]. Veletsos, A.S., and Meek, J.W, Dynamic behavior of building-foundation systems, J.Earthquake Engrg. Struct. Dyn., 3(2),121–
138, 1974.
[5]. Veletsos, A. S., and Nair, V. V, Seismic interaction of structures on hysteretic foundations,J. Struct. Engrg., ASCE, 101(1), 109–
129, 1975.
[6]. Khalil.L, Sadek.Marwan, Shahrouri.Isam, Influence de l’interaction sol structure ISS sur la fréquence fondamentale des bâtiments,
XXIV Emes Rencontres universitaires de génie civil, Montpellier, 1-2 juin (2006).
[7]. R.Souloumiac, Interaction sol-structure, méthode simplifiée, Socotec, 1984.
[8]. ATC-3, Tentative Provisions for the Development of seismic regulations for buildings, ch.6, 1978.
[9]. Norris .C.H, Wilbur.J.B, Utku.S, Elementary Structural Analysis, Mc Graw Hill, 1976.
[10]. Ayman Ismail, Effect of Soil Flexibility on Seismic Performance of 3-D Frames, IOSR Journal of Mechanical and Civil
Engineering (IOSR-JMCE) e-ISSN: 2278-1684,p-ISSN: 2320-334X, Volume 11, Issue 4 Ver. II, PP 135-143, Jul- Aug. 2014.
[11]. Michael James Givens, Dynamic Soil-Structure Interaction of Instrumented Buildings and Test Structures, doctoral dissertation,
university of California - Los Angeles, 2013
[12]. Mylonakis, George and Gazetas, George, Seismic soil structure interaction: Beneficial or Detrimental?, Journal of Earthquake
Engineering, 4: 3, 277 — 301, 2000
[13]. E.N.Rovithis, K.D. Pitilakis, G.E. Mylonakis, Seismic analysis of coupled soil pile structure systems leading to the definition of a
pseudo natural SSI frequency, Soil dynmacis and earthquake engineering 1005-1015, 2009
[14]. Javier Avilés, Luis E. Pérez-Rocha, Evaluation of interaction effects on the system period and the system damping due to
foundation embedment and layer depth, Soil Dynamics and Earthquake Engineering 15 11-27 ,Elsevier Science Limited, 1996.
[15]. Règles Parasismiques Algériennes 99-03, OPU, Algérie, 2003.
[16]. Gazetas, G. and Mylonakis, G, Seismic Soil-Structure Interaction: New Evidence and Emerging Issues, Emerging Issues Paper,
Geotechnical Special Publication No 75, ASCE, Vol III., pp. 1119-1174, 1998.
[17]. Gazetas, G. and Mylonakis, G., Seismic soil-structure interaction: beneficial or detrimental, Journal Earthquake, vol. 4, No 3, 277-
301, 2000.

[18]. Hamid reza Tabatabaiefar, Ali Massumi, A simplified method to determine seismic responses of reinforced concrete moment
resisting building frames under influence of soil-structure interaction. Soil dynamics and erathquake engineering, 30 1259-
1267,2010.
[19]. H.K Chinmayi, B.R Jayalekshmi, Soil-structure interaction analysis of RC frame shear wall buildings over raft foundations under
seismic loading, International Journal of Scientific & Engineering Research Volume 4, Issue 5, May-2013
[20]. Jayalekshmi B.R, Chinmayi H.K , Effect of soil flexibility on lateral natural period in RC framed buildings with shear wall,
International Journal of Innovative Research in Science, Engineering and Technology Vol. 2, Issue 6, June 2013.
[21]. I. Kraus & D. Džakić , Soil-structure interaction effects on seismic behaviour of reinforced concrete frames, 50 SE –EEE University
of Osijek, Faculty of Civil Engineering Osijek,Croatia 2013.
[22]. Jian Zhang, Yuchuan Tang, Dimensional analysis of structures with translating and rocking foundations under near fault ground
motions, Soil dynamics and earthquake engineering 1330-1346, 2009.
Captions to tables
Table. 1: Geotechnical specification of the utilized soils in research.
Soil type Elastic
Module
E (Kn/m²)
Shear Module
G (Kn/m²)
Poisson
Ratio

Mass
Density
 (Kn.S²/m4
)
Sol (Bars) Shear
Wave
Vs(m/s)
Stiff - Site S1 1640000 648000 0.28 1.8 2 600
Medium - Site S2 494500 180800 0.39 1.75 1.3 320
Soft - Site S3 and S4 93500 33500 0.4 1.50 0.6 150
Table. 2: Variation of fundamental lateral natural period without SSI
Dimensional specification of the studied
frames
Fundamental natural periods without soil-structure interaction WSSI
Soil
Type
Numberof
Bay
Numberof
stories
Story
Height(m)
StoryWidth
(m)
T (s) Comparison
Exact RPA
2003
ADELI
Model
T exact
/
T RPA2003
TADELI
/
T RPA2003
T exact
/
T ADELI
S1-S2-S3andS4
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
8
8
12
12
16
16
20
20
24
28
10
30
10
30
10
30
10
30
10
10
0.176
0.178
0.219
0.222
0.266
0.270
0.346
0.348
0.460
0.583
0.356
0.356
0.484
0.484
0.600
0.600
0.700
0.700
0.813
0.912
0.151
0.157
0.228
0.236
0.304
0.315
0.343
0.354
0.412
0.481
0.494
0.500
0.452
0.458
0.443
0.450
0.494
0.497
0.565
0.639
Mean = 0.499
Devation =0.05
0.424
0.441
0.471
0.487
0.506
0.525
0.490
0.505
0.506
0.527
Mean = 0.484
Devation=0.01
1.165
1.133
0.960
0.940
0.875
0.857
1.008
0.983
1.116
1.212
Mean = 1.025
Devation=0.09
Table. 3: Factor of the relative stiffness between structure and soil.
1/ = H / Vs T
Soil
Type
Frame
Type RPA 2003 Proposed Model
StiffSoil-S1
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.037
0.037
0.041
0.041
0.044
0.044
0.047
0.047
0.049
0.051
Mean = 0.043
0.088
0.084
0.087
0.084
0.087
0.084
0.097
0.094
0.097
0.097
Mean = 0.089
MediumSoil-S2
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.070
0.070
0.077
0.077
0.083
0.083
0.089
0.089
0.092
0.095
Mean = 0.082
0.165
0.159
0.164
0.158
0.164
0.158
0.182
0.176
0.182
0.181
Mean = 0.168

SoftSoil–S3andS4
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.149
0.149
0.165
0.165
0.177
0.177
0.190
0.190
0.196
0.204
Mean = 0.176
0.353
0.339
0.350
0.338
0.350
0.338
0.388
0.376
0.388
0.388
Mean = 0.360
Table. 4: Variation of fundamental lateral natural period with SSI.
(4a) WS = 2 WSt
SoilType
FrameType
b:bayands:storey
Natural Periods with Soil-Structure Interaction SSI
Veletsos
Deleuze-Newmark
Gazetas
T*
Proposed Model with Isolated footings
WS = 2 WSt
IF = 0 IF = 0.05 ISt IF = 0.1 ISt
WF=0WSt
WF=0.25WSt
WF=0.5WSt
WF=0WSt
WF=0.25WSt
WF=0.5WSt
WF=0WSt
WF=0.25WSt
WF=0.5WSt
MediumSoil-S2r=1.05
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.374
0.406
0.491
0.505
0.603
0.611
0.702
0.704
0.814
0.913
0.24689
0.23622
0.36980
0.35029
0.49631
0.46697
0.62469
0.58452
0.75475
0.88626
0.24781
0.23714
0.37030
0.35080
0.49659
0.46729
0.62484
0.58470
0.75482
0.88626
0.268
0.277
0.404
0.418
0.541
0.559
0.612
0.635
0.737
0.863
0.278
0.288
0.421
0.435
0.563
0.582
0.637
0.661
0.767
0.899
0.289
0.299
0.436
0.451
0.585
0.604
0.661
0.686
0.796
0.932
0.268
0.277
0.404
0.418
0.541
0.559
0.612
0.635
0.737
0.863
0.278
0.288
0.420
0.435
0.563
0.582
0.637
0.661
0.767
0.898
0.289
0.299
0.436
0.451
0.585
0.604
0.661
0.686
0.796
0.932
0.268
0.277
0.404
0.418
0.541
0.559
0.611
0.634
0.736
0.862
0.278
0.288
0.420
0.435
0.563
0.582
0.636
0.660
0.766
0.898
0.289
0.299
0.436
0.451
0.584
0.604
0.661
0.685
0.795
0.931
SoftSoilS3andS4r=1.10
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.372
0.402
0.493
0.511
0.607
0.621
0.705
0.714
0.818
0.916
0.29092
0.27413
0.40929
0.37734
0.53954
0.49042
0.65970
0.59900
0.79931
0.94120
0.29681
0.28013
0.41201
0.38056
0.54037
0.49209
0.65898
0.59908
0.79806
0.93942
0.274
0.284
0.413
0.428
0.554
0.572
0.626
0.650
0.754
0.883
0.285
0.295
0.430
0.445
0.577
0.596
0.652
0.676
0.785
0.919
0.296
0.306
0.447
0.462
0.598
0.618
0.676
0.702
0.814
0.954
0.274
0.284
0.413
0.428
0.554
0.572
0.626
0.649
0.754
0.883
0.285
0.295
0.430
0.445
0.576
0.595
0.651
0.676
0.785
0.919
0.296
0.306
0.447
0.462
0.598
0.618
0.676
0.701
0.814
0.953
0.274
0.284
0.413
0.428
0.554
0.572
0.626
0.649
0.753
0.882
0.285
0.295
0.430
0.445
0.576
0.595
0.651
0.676
0.784
0.918
0.296
0.306
0.447
0.462
0.598
0.618
0.676
0.701
0.814
0.953

(4b) WS = 5 WSt
SoilType
FrameType
b:bayands:storey
Natural Periods with Soil-Structure Interaction SSI
Veletsos
Deleuze-Newmark
Gazetas
T*
Proposed Model with Isolated footings
WS = 5 WSt
IF = 0 IF = 0.05 ISt IF = 0.1 ISt
WF=0WSt
WF=0.25
WSt
WF=0.5
WSt
WF=0WSt
WF=0.25
WSt
WF=0.5
WSt
WF=0WSt
WF=0.25
WSt
WF=0.5
WSt
MediumSoil-S2r=1.05
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.374
0.406
0.491
0.505
0.603
0.611
0.702
0.704
0.814
0.913
0.24689
0.23622
0.36980
0.35029
0.49631
0.46697
0.62469
0.58452
0.75475
0.88626
0.24781
0.23714
0.37030
0.35080
0.49659
0.46729
0.62484
0.58470
0.75482
0.88626
0.379
0.392
0.572
0.591
0.766
0.791
0.865
0.898
1.042
1.221
0.386
0.400
0.583
0.603
0.782
0.807
0.883
0.917
1.064
1.246
0.394
0.408
0.595
0.615
0.797
0.823
0.901
0.935
1.085
1.271
0.379
0.392
0.572
0.591
0.766
0.791
0.865
0.898
1.042
1.220
0.386
0.400
0.583
0.603
0.781
0.807
0.883
0.916
1.064
1.246
0.394
0.408
0.595
0.615
0.797
0.823
0.901
0.935
1.085
1.270
0.379
0.392
0.571
0.591
0.765
0.791
0.865
0.897
1.042
1.220
0.386
0.400
0.583
0.603
0.781
0.807
0.883
0.916
1.063
1.245
0.394
0.408
0.595
0.615
0.797
0.823
0.900
0.934
1.084
1.270
SoftSoilS3andS4r=1.10
2b 2s
6b 2s
2b 3s
6b 3s
2b 4s
6b 4s
2b 5s
6b 5s
2b 6s
2b 7s
0.372
0.402
0.493
0.511
0.607
0.621
0.705
0.714
0.818
0.916
0.29092
0.27413
0.40929
0.37734
0.53954
0.49042
0.65970
0.59900
0.79931
0.94120
0.29681
0.28013
0.41201
0.38056
0.54037
0.49209
0.65898
0.59908
0.79806
0.93942
0.387
0.401
0.585
0.605
0.784
0.809
0.886
0.919
1.067
1.249
0.395
0.410
0.597
0.618
0.800
0.826
0.904
0.938
1.089
1.275
0.403
0.418
0.609
0.630
0.816
0.842
0.922
0.957
1.110
1.300
0.387
0.401
0.585
0.605
0.783
0.809
0.885
0.919
1.066
1.248
0.395
0.410
0.597
0.618
0.800
0.826
0.904
0.937
1.088
1.274
0.403
0.418
0.609
0.630
0.815
0.842
0.921
0.956
1.110
1.299
0.387
0.401
0.585
0.605
0.783
0.809
0.885
0.918
1.066
1.248
0.395
0.410
0.597
0.618
0.799
0.826
0.903
0.937
1.088
1.274
0.403
0.418
0.609
0.630
0.815
0.842
0.921
0.956
1.109
1.299
9. Captions to figures
Fig. 1: Schematic illustration of SSI Model.

Fig. 2: Variation of change in period of vibration without SSI.
Fig. 3: Variation of the relative stiffness between structure and soil.
(3a)

(3b)
Fig. 4: Variation of change in period of vibration with SSI considering Ws = 2WSt , If = 0.05 ISt and
Wf = 0.25 WSt.
(4a)
(4b)
Fig. 5: Periods of soil-structure systems for various soil mass considering WF = 0.25WSt , If = 0.05 ISt .
(5a)

(5b)

Q01222110120

More Related Content

Q01222110120