Queueing 2

Queueing Theory

Ivo Adan and Jacques Resing

Department of Mathematics and Computing Science
Eindhoven University of Technology
P.O. Box 513, 5600 MB Eindhoven, The Netherlands

February 28, 2002

Contents

1 Introduction 7
1.1 Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2 Basic concepts from probability theory 11
2.1 Random variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.2 Generating function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.3 Laplace-Stieltjes transform . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.4 Useful probability distributions . . . . . . . . . . . . . . . . . . . . . . . . 12
2.4.1 Geometric distribution . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.4.2 Poisson distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.4.3 Exponential distribution . . . . . . . . . . . . . . . . . . . . . . . . 13
2.4.4 Erlang distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.4.5 Hyperexponential distribution . . . . . . . . . . . . . . . . . . . . . 15
2.4.6 Phase-type distribution . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.5 Fitting distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.6 Poisson process . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.7 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

3 Queueing models and some fundamental relations 23
3.1 Queueing models and Kendall’s notation . . . . . . . . . . . . . . . . . . . 23
3.2 Occupation rate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.3 Performance measures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.4 Little’s law . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.5 PASTA property . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.6 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

4 M/M/1 queue 29
4.1 Time-dependent behaviour . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.2 Limiting behavior . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.2.1 Direct approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.2.2 Recursion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.2.3 Generating function approach . . . . . . . . . . . . . . . . . . . . . 32
4.2.4 Global balance principle . . . . . . . . . . . . . . . . . . . . . . . . 32

3

4.3 Mean performance measures . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4.4 Distribution of the sojourn time and the waiting time . . . . . . . . . . . . 33
4.5 Priorities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.5.1 Preemptive-resume priority . . . . . . . . . . . . . . . . . . . . . . 36
4.5.2 Non-preemptive priority . . . . . . . . . . . . . . . . . . . . . . . . 37
4.6 Busy period . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.6.1 Mean busy period . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.6.2 Distribution of the busy period . . . . . . . . . . . . . . . . . . . . 38
4.7 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.8 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

5 M/M/c queue 43
5.1 Equilibrium probabilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.2 Mean queue length and mean waiting time . . . . . . . . . . . . . . . . . . 44
5.3 Distribution of the waiting time and the sojourn time . . . . . . . . . . . . 46
5.4 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
5.5 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

6 M/Er /1 queue 49
6.1 Two alternative state descriptions . . . . . . . . . . . . . . . . . . . . . . . 49
6.2 Equilibrium distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
6.3 Mean waiting time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
6.4 Distribution of the waiting time . . . . . . . . . . . . . . . . . . . . . . . . 53
6.5 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
6.6 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

7 M/G/1 queue 59
7.1 Which limiting distribution? . . . . . . . . . . . . . . . . . . . . . . . . . . 59
7.2 Departure distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
7.3 Distribution of the sojourn time . . . . . . . . . . . . . . . . . . . . . . . . 64
7.4 Distribution of the waiting time . . . . . . . . . . . . . . . . . . . . . . . . 66
7.5 Lindley’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
7.6 Mean value approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
7.7 Residual service time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
7.8 Variance of the waiting time . . . . . . . . . . . . . . . . . . . . . . . . . . 70
7.9 Distribution of the busy period . . . . . . . . . . . . . . . . . . . . . . . . 71
7.10 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
7.11 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

8 G/M/1 queue 79
8.1 Arrival distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
8.2 Distribution of the sojourn time . . . . . . . . . . . . . . . . . . . . . . . . 83
8.3 Mean sojourn time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84

4

8.4 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
8.5 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

9 Priorities 87
9.1 Non-preemptive priority . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
9.2 Preemptive-resume priority . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
9.3 Shortest processing time ﬁrst . . . . . . . . . . . . . . . . . . . . . . . . . 90
9.4 A conservation law . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
9.5 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

10 Variations of the M/G/1 model 97
10.1 Machine with setup times . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
10.1.1 Exponential processing and setup times . . . . . . . . . . . . . . . . 97
10.1.2 General processing and setup times . . . . . . . . . . . . . . . . . . 98
10.1.3 Threshold setup policy . . . . . . . . . . . . . . . . . . . . . . . . . 99
10.2 Unreliable machine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
10.2.1 Exponential processing and down times . . . . . . . . . . . . . . . . 100
10.2.2 General processing and down times . . . . . . . . . . . . . . . . . . 101
10.3 M/G/1 queue with an exceptional ﬁrst customer in a busy period . . . . . 103
10.4 M/G/1 queue with group arrivals . . . . . . . . . . . . . . . . . . . . . . . 104
10.5 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107

11 Insensitive systems 111
11.1 M/G/∞ queue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
11.2 M/G/c/c queue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
11.3 Stable recursion for B(c, ρ) . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
11.4 Java applet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
11.5 Exercises . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

Bibliography 119

Index 121

Solutions to Exercises 123

5

Chapter 1

Introduction

In general we do not like to wait. But reduction of the waiting time usually requires extra
investments. To decide whether or not to invest, it is important to know the effect of
the investment on the waiting time. So we need models and techniques to analyse such
situations.
In this course we treat a number of elementary queueing models. Attention is paid
to methods for the analysis of these models, and also to applications of queueing models.
Important application areas of queueing models are production systems, transportation and
stocking systems, communication systems and information processing systems. Queueing
models are particularly useful for the design of these system in terms of layout, capacities
and control.
In these lectures our attention is restricted to models with one queue. Situations with
multiple queues are treated in the course “Networks of queues.” More advanced techniques
for the exact, approximative and numerical analysis of queueing models are the subject of
the course “Algorithmic methods in queueing theory.”
The organization is as follows. Chapter 2 first discusses a number of basic concepts
and results from probability theory that we will use. The most simple interesting queueing
model is treated in chapter 4, and its multi server version is treated in the next chapter.
Models with more general service or interarrival time distributions are analysed in the
chapters 6, 7 and 8. Some simple variations on these models are discussed in chapter 10.
Chapter 9 is devoted to queueing models with priority rules. The last chapter discusses
some insentive systems.
The text contains a lot of exercises and the reader is urged to try these exercises. This
is really necessary to acquire skills to model and analyse new situations.

1.1 Examples
Below we briefly describe some situations in which queueing is important.

Example 1.1.1 Supermarket.
How long do customers have to wait at the checkouts? What happens with the waiting

7

time during peak-hours? Are there enough checkouts?

Example 1.1.2 Production system.
A machine produces different types of products.
What is the production lead time of an order? What is the reduction in the lead time
when we have an extra machine? Should we assign priorities to the orders?

Example 1.1.3 Post office.
In a post office there are counters specialized in e.g. stamps, packages, financial transac-
tions, etc.
Are there enough counters? Separate queues or one common queue in front of counters
with the same specialization?

Example 1.1.4 Data communication.
In computer communication networks standard packages called cells are transmitted over
links from one switch to the next. In each switch incoming cells can be buffered when the
incoming demand exceeds the link capacity. Once the buffer is full incoming cells will be
lost.
What is the cell delay at the switches? What is the fraction of cells that will be lost? What
is a good size of the buffer?

Example 1.1.5 Parking place.
They are going to make a new parking place in front of a super market.
How large should it be?

Example 1.1.6 Assembly of printed circuit boards.
Mounting vertical components on printed circuit boards is done in an assembly center
consisting of a number of parallel insertion machines. Each machine has a magazine to
store components.
What is the production lead time of the printed circuit boards? How should the components
necessary for the assembly of printed circuit boards be divided among the machines?

Example 1.1.7 Call centers of an insurance company.
Questions by phone, regarding insurance conditions, are handled by a call center. This call
center has a team structure, where each team helps customers from a specific region only.
How long do customers have to wait before an operator becomes available? Is the number
of incoming telephone lines enough? Are there enough operators? Pooling teams?

Example 1.1.8 Main frame computer.
Many cashomats are connected to a big main frame computer handling all financial trans-
actions.
Is the capacity of the main frame computer sufficient? What happens when the use of
cashomats increases?

8

Example 1.1.9 Toll booths.
Motorists have to pay toll in order to pass a bridge. Are there enough toll booths?

Example 1.1.10 Traﬃc lights.
How do we have to regulate traﬃc lights such that the waiting times are acceptable?

9

Chapter 2

Basic concepts from probability
theory

This chapter is devoted to some basic concepts from probability theory.

2.1 Random variable
Random variables are denoted by capitals, X, Y , etc. The expected value or mean of X is
denoted by E(X) and its variance by σ 2 (X) where σ(X) is the standard deviation of X.
An important quantity is the coefficient of variation of the positive random variable X
defined as
σ(X)
cX = .
E(X)
The coefficient of variation is a (dimensionless) measure of the variability of the random
variable X.

2.2 Generating function
Let X be a nonnegative discrete random variable with P (X = n) = p(n), n = 0, 1, 2, . . ..
Then the generating function PX (z) of X is defined as
∞
X
PX (z) = E(z ) = p(n)z n .
n=0

Note that |PX (z)| ≤ 1 for all |z| ≤ 1. Further
PX (0) = p(0), PX (1) = 1, PX (1) = E(X),
and, more general,
(k)
PX (1) = E(X(X − 1) · · · (X − k + 1)),

11

where the superscript (k) denotes the kth derivative. For the generating function of the
sum Z = X + Y of two independent discrete random variables X and Y , it holds that
PZ (z) = PX (z) · PY (z).
When Z is with probability q equal to X and with probability 1 − q equal to Y , then
PZ (z) = qPX (z) + (1 − q)PY (z).

2.3 Laplace-Stieltjes transform
The Laplace-Stieltjes transform X(s) of a nonnegative random variable X with distribution
function F (·), is deﬁned as
∞
X(s) = E(e−sX ) = e−sx dF (x), s ≥ 0.
x=0

When the random variable X has a density f (·), then the transform simpliﬁes to
∞
X(s) = e−sx f (x)dx, s ≥ 0.
x=0

Note that |X(s)| ≤ 1 for all s ≥ 0. Further
X(0) = 1, X (0) = −E(X), X (k) (0) = (−1)k E(X k ).
For the transform of the sum Z = X + Y of two independent random variables X and Y ,
it holds that
Z(s) = X(s) · Y (s).
When Z is with probability q equal to X and with probability 1 − q equal to Y , then
Z(s) = q X(s) + (1 − q)Y (s).

2.4 Useful probability distributions
This section discusses a number of important distributions which have been found useful
for describing random variables in many applications.

2.4.1 Geometric distribution
A geometric random variable X with parameter p has probability distribution
P (X = n) = (1 − p)pn , n = 0, 1, 2, . . .
For this distribution we have
1−p p p 1
PX (z) = , E(X) = , σ 2 (X) = , c2 = .
X
1 − pz 1−p (1 − p)2 p

12

2.4.2 Poisson distribution
A Poisson random variable X with parameter µ has probability distribution

µn −µ
P (X = n) = e , n = 0, 1, 2, . . .
n!

For the Poisson distribution it holds that

1
PX (z) = e−µ(1−z) , E(X) = σ 2 (X) = µ, c2 =
X .
µ

2.4.3 Exponential distribution
The density of an exponential distribution with parameter µ is given by

f (t) = µe−µt , t > 0.

The distribution function equals

F (t) = 1 − e−µt , t ≥ 0.

For this distribution we have

µ 1 1
X(s) = , E(X) = , σ 2 (X) = , cX = 1.
µ+s µ µ2

An important property of an exponential random variable X with parameter µ is the
memoryless property. This property states that for all x ≥ 0 and t ≥ 0,

P (X > x + t|X > t) = P (X > x) = e−µx .

So the remaining lifetime of X, given that X is still alive at time t, is again exponentially
distributed with the same mean 1/µ. We often use the memoryless property in the form

P (X < t + ∆t|X > t) = 1 − e−µ∆t = µ∆t + o(∆t), (∆t → 0), (2.1)

where o(∆t), (∆t → 0), is a shorthand notation for a function, g(∆t) say, for which
g(∆t)/∆t tends to 0 when ∆t → 0 (see e.g. [4]).
If X1 , . . . , Xn are independent exponential random variables with parameters µ1 , . . . , µn
respectively, then min(X1 , . . . , Xn ) is again an exponential random variable with parameter
µ1 + · · · + µn and the probability that Xi is the smallest one is given by µi /(µ1 + · · · + µn ),
i = 1, . . . , n. (see exercise 1).

13

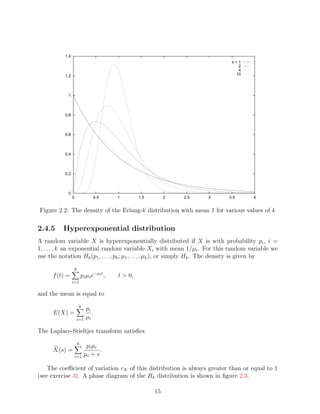
2.4.4 Erlang distribution
A random variable X has an Erlang-k (k = 1, 2, . . .) distribution with mean k/µ if X
is the sum of k independent random variables X1 , . . . , Xk having a common exponential
distribution with mean 1/µ. The common notation is Ek (µ) or briefly Ek . The density of
an Ek (µ) distribution is given by
(µt)k−1 −µt
f (t) = µ e , t > 0.
(k − 1)!
The distribution function equals
k−1
(µt)j −µt
F (t) = 1 − e , t ≥ 0.
j=0 j!

The parameter µ is called the scale parameter, k is the shape parameter. A phase diagram
of the Ek distribution is shown in figure 2.1.

µ µ µ

1 2 k

Figure 2.1: Phase diagram for the Erlang-k distribution with scale parameter µ

In figure 2.2 we display the density of the Erlang-k distribution with mean 1 (so µ = k)
for various values of k.
The mean, variance and squared coefficient of variation are equal to
k k 1
E(X) = , σ 2 (X) = , c2 =
X .
µ µ2 k
The Laplace-Stieltjes transform is given by
k
µ
X(s) = .
µ+s
A convenient distribution arises when we mix an Ek−1 and Ek distribution with the
same scale parameters. The notation used is Ek−1,k . A random variable X has an Ek−1,k (µ)
distribution, if X is with probability p (resp. 1 − p) the sum of k − 1 (resp. k) independent
exponentials with common mean 1/µ. The density of this distribution has the form
(µt)k−2 −µt (µt)k−1 −µt
f (t) = pµ e + (1 − p)µ e , t > 0,
(k − 2)! (k − 1)!
where 0 ≤ p ≤ 1. As p runs from 1 to 0, the squared coefficient of variation of the
mixed Erlang distribution varies from 1/(k − 1) to 1/k. It will appear (later on) that this
distribution is useful for fitting a distribution if only the first two moments of a random
variable are known.

14

1.4
k=1
2
4
1.2 10

1

0.8

0.6

0.4

0.2

0
0 0.5 1 1.5 2 2.5 3 3.5 4

Figure 2.2: The density of the Erlang-k distribution with mean 1 for various values of k

2.4.5 Hyperexponential distribution
A random variable X is hyperexponentially distributed if X is with probability pi , i =
1, . . . , k an exponential random variable Xi with mean 1/µi . For this random variable we
use the notation Hk (p1 , . . . , pk ; µ1 , . . . , µk ), or simply Hk . The density is given by

k
f (t) = pi µi e−µi t , t > 0,
i=1

and the mean is equal to
k
pi
E(X) = .
i=1 µi

The Laplace-Stieltjes transform satisfies
k
p i µi
X(s) = .
i=1 µi + s

The coefficient of variation cX of this distribution is always greater than or equal to 1
(see exercise 3). A phase diagram of the Hk distribution is shown in figure 2.3.

15

µ1

1
p1

pk
k

µk

Figure 2.3: Phase diagram for the hyperexponential distribution

2.4.6 Phase-type distribution
The preceding distributions are all special cases of the phase-type distribution. The notation
is P H. This distribution is characterized by a Markov chain with states 1, . . . , k (the so-
called phases) and a transition probability matrix P which is transient. This means that
P n tends to zero as n tends to infinity. In words, eventually you will always leave the
Markov chain. The residence time in state i is exponentially distributed with mean 1/µi ,
and the Markov chain is entered with probability pi in state i, i = 1, . . . , k. Then the
random variable X has a phase-type distribution if X is the total residence time in the
preceding Markov chain, i.e. X is the total time elapsing from start in the Markov chain
till departure from the Markov chain.
We mention two important classes of phase-type distributions which are dense in the
class of all non-negative distribution functions. This is meant in the sense that for any
non-negative distribution function F (·) a sequence of phase-type distributions can be found
which pointwise converges at the points of continuity of F (·). The denseness of the two
classes makes them very useful as a practical modelling tool. A proof of the denseness can
be found in [23, 24]. The first class is the class of Coxian distributions, notation Ck , and
the other class consists of mixtures of Erlang distributions with the same scale parameters.
The phase representations of these two classes are shown in the figures 2.4 and 2.5.

µ1 µ2 µk
p1 p2 pk −1
1 2 k

1 − p1 1 − p2 1 − pk −1

Figure 2.4: Phase diagram for the Coxian distribution

A random variable X has a Coxian distribution of order k if it has to go through up to
at most k exponential phases. The mean length of phase n is 1/µn , n = 1, . . . , k. It starts
in phase 1. After phase n it comes to an end with probability 1 − pn and it enters the next
phase with probability pn . Obviously pk = 0. For the Coxian-2 distribution it holds that

16

µ

1

p1
1 2

p2 µ µ

pk

1 2 k

µ µ µ

Figure 2.5: Phase diagram for the mixed Erlang distribution

the squared coefficient of variation is greater than or equal to 0.5 (see exercise 8).
A random variable X has a mixed Erlang distribution of order k if it is with probability
pn the sum of n exponentials with the same mean 1/µ, n = 1, . . . , k.

2.5 Fitting distributions
In practice it often occurs that the only information of random variables that is available
is their mean and standard deviation, or if one is lucky, some real data. To obtain an
approximating distribution it is common to fit a phase-type distribution on the mean,
E(X), and the coefficient of variation, cX , of a given positive random variable X, by using
the following simple approach.
In case 0 < cX < 1 one fits an Ek−1,k distribution (see subsection 2.4.4). More specifi-
cally, if
1 1
≤ c2 ≤
X ,
k k−1
for certain k = 2, 3, . . ., then the approximating distribution is with probability p (resp.
1 − p) the sum of k − 1 (resp. k) independent exponentials with common mean 1/µ. By
choosing (see e.g. [28])

1 k−p
p= [kc2 − {k(1 + c2 ) − k 2 c2 }1/2 ], µ= ,
1 + cX X
2 X X
E(X)

the Ek−1,k distribution matches E(X) and cX .
In case cX ≥ 1 one fits a H2 (p1 , p2 ; µ1 , µ2 ) distribution. The hyperexponential distribu-
tion however is not uniquely determined by its first two moments. In applications, the H2

17

distribution with balanced means is often used. This means that the normalization
p1 p2
=
µ1 µ2
is used. The parameters of the H2 distribution with balanced means and fitting E(X) and
cX (≥ 1) are given by
 
1 c2 − 1 
X
p1 = 1 + , p2 = 1 − p1 ,
2 c2 + 1
X

2p1 2p2
µ1 = , µ1 = .
E(X) E(X)

In case c2 ≥ 0.5 one can also use a Coxian-2 distribution for a two-moment fit. The
X
following set is suggested by [18],
µ1 = 2/E(X), p1 = 0.5/c2 ,
X µ2 = µ1 p1 .
It also possible to make a more sophisticated use of phase-type distributions by, e.g.,
trying to match the first three (or even more) moments of X or to approximate the shape
of X (see e.g. [29, 11, 13]).
Phase-type distributions may of course also naturally arise in practical applications.
For example, if the processing of a job involves performing several tasks, where each task
takes an exponential amount of time, then the processing time can be described by an
Erlang distribution.

2.6 Poisson process
Let N (t) be the number of arrivals in [0, t] for a Poisson process with rate λ, i.e. the time
between successive arrivals is exponentially distributed with parameter λ and independent
of the past. Then N (t) has a Poisson distribution with parameter λt, so
(λt)k −λt
P (N (t) = k) = e , k = 0, 1, 2, . . .
k!
The mean, variance and coefficient of variation of N (t) are equal to (see subsection 2.4.2)
1
E(N (t)) = λt, σ 2 (N (t)) = λt, c2 (t) =
N .
λt
From (2.1) it is easily verified that
P (arrival in (t, t + ∆t]) = λ∆t + o(∆t), (∆t → 0).
Hence, for small ∆t,
P (arrival in (t, t + ∆t]) ≈ λ∆t. (2.2)

18

So in each small time interval of length ∆t the occurence of an arrival is equally likely. In
other words, Poisson arrivals occur completely random in time. In ﬁgure 2.6 we show a
realization of a Poisson process and an arrival process with Erlang-10 interarrival times.
Both processes have rate 1. The ﬁgure illustrates that Erlang arrivals are much more
equally spread out over time than Poisson arrivals.

Poisson
t

Erlang-10
t

Figure 2.6: A realization of Poisson arrivals and Erlang-10 arrivals, both with rate 1

The Poisson process is an extremely useful process for modelling purposes in many
practical applications, such as, e.g. to model arrival processes for queueing models or
demand processes for inventory systems. It is empirically found that in many circumstances
the arising stochastic processes can be well approximated by a Poisson process.
Next we mention two important properties of a Poisson process (see e.g. [20]).

(i) Merging.
Suppose that N1 (t) and N2 (t) are two independent Poisson processes with respective
rates λ1 and λ2 . Then the sum N1 (t) + N2 (t) of the two processes is again a Poisson
process with rate λ1 + λ2 .

(ii) Splitting.
Suppose that N (t) is a Poisson process with rate λ and that each arrival is marked
with probability p independent of all other arrivals. Let N1 (t) and N2 (t) denote
respectively the number of marked and unmarked arrivals in [0, t]. Then N1 (t) and
N2 (t) are both Poisson processes with respective rates λp and λ(1 − p). And these
two processes are independent.

So Poisson processes remain Poisson processes under merging and splitting.

19

2.7 Exercises
Exercise 1.
Let X1 , . . . , Xn be independent exponential random variables with mean E(Xi ) = 1/µi ,
i = 1, . . . , n. Define

Yn = min(X1 , . . . , Xn ), Zn = max(X1 , . . . , Xn ).

(i) Determine the distributions of Yn and Zn .

(ii) Show that the probability that Xi is the smallest one among X1 , . . . , Xn is equal to
µi /(µ1 + · · · + µn ), i = 1, . . . , n.

Exercise 2.
Let X1 , X2 , . . . be independent exponential random variables with mean 1/µ and let N be
a discrete random variable with

P (N = k) = (1 − p)pk−1 , k = 1, 2, . . . ,

where 0 ≤ p < 1 (i.e. N is a shifted geometric random variable). Show that S defined as
N
S= Xn
n=1

is again exponentially distributed with parameter (1 − p)µ.
Exercise 3.
Show that the coefficient of variation of a hyperexponential distribution is greater than or
equal to 1.
Exercise 4. (Poisson process)
Suppose that arrivals occur at T1 , T2 , . . .. The interarrival times An = Tn − Tn−1 are
independent and have common exponential distribution with mean 1/λ, where T0 = 0 by
convention. Let N (t) denote the number of arrivals is [0, t] and define for n = 0, 1, 2, . . .

pn (t) = P (N (t) = n), t > 0.

(i) Determine p0 (t).

(ii) Show that for n = 1, 2, . . .

pn (t) = −λpn (t) + λpn−1 (t), t > 0,

with initial condition pn (0) = 0.

(iii) Solve the preceding differential equations for n = 1, 2, . . .

20

Suppose that arrivals occur at T1 , T2 , . . .. The interarrival times An = Tn − Tn−1 are
independent and have common exponential distribution with mean 1/λ, where T0 = 0 by
convention. Let N (t) denote the number of arrivals is [0, t] and deﬁne for n = 0, 1, 2, . . .

pn (t) = P (N (t) = n), t > 0.

(i) Determine p0 (t).

(ii) Show that for n = 1, 2, . . .

t
pn (t) = pn−1 (t − x)λe−λx dx, t > 0.
0

(iii) Solve the preceding integral equations for n = 1, 2, . . .

Prove the properties (i) and (ii) of Poisson processes, formulated in section 2.6.
Exercise 7. (Fitting a distribution)
Suppose that processing a job on a certain machine takes on the average 4 minutes with a
standard deviation of 3 minutes. Show that if we model the processing time as a mixture
of an Erlang-1 (exponential) distribution and an Erlang-2 distribution with density

f (t) = pµe−µt + (1 − p)µ2 te−µt ,

the parameters p and µ can be chosen in such a way that this distribution matches the
mean and standard deviation of the processing times on the machine.
Exercise 8.
Consider a random variable X with a Coxian-2 distribution with parameters µ1 and µ2
and branching probability p1 .

(i) Show that c2 ≥ 0.5.
X

(ii) Show that if µ1 < µ2 , then this Coxian-2 distribution is identical to the Coxian-
2 distribution with parameters µ1 , µ2 and p1 where µ1 = µ2 , µ2 = µ1 and p1 =
ˆ ˆ ˆ ˆ ˆ ˆ
1 − (1 − p1 )µ1 /µ2 .

Part (ii) implies that for any Coxian-2 distribution we may assume without loss of generality
that µ1 ≥ µ2 .
Exercise 9.
Let X and Y be exponentials with parameters µ and λ, respectively. Suppose that λ < µ.
Let Z be equal to X with probability λ/µ and equal to X + Y with probability 1 − λ/µ.
Show that Z is an exponential with parameter λ.

21

Exercise 10.
Consider a H2 distribution with parameters µ1 > µ2 and branching probabilities q1 and
q2 , respectively. Show that the C2 distribution with parameters µ1 and µ2 and branching
probability p1 given by

p1 = 1 − (q1 µ1 + q2 µ2 )/µ1 ,

is equivalent to the H2 distribution.
Exercise 11. (Poisson distribution)
Let X1 , . . . , Xn be independent Poisson random variables with means µ1 , . . . , µn , respec-
tively. Show that the sum X1 + · · · + Xn is Poisson distributed with mean µ1 + · · · + µn .

22

Chapter 3

Queueing models and some
fundamental relations

In this chapter we describe the basic queueing model and we discuss some important fun-
damental relations for this model. These results can be found in every standard textbook
on this topic, see e.g. [14, 20, 28].

3.1 Queueing models and Kendall’s notation
The basic queueing model is shown in ﬁgure 3.1. It can be used to model, e.g., machines
or operators processing orders or communication equipment processing information.

Figure 3.1: Basic queueing model

Among others, a queueing model is characterized by:

• The arrival process of customers.
Usually we assume that the interarrival times are independent and have a common
distribution. In many practical situations customers arrive according to a Poisson
stream (i.e. exponential interarrival times). Customers may arrive one by one, or
in batches. An example of batch arrivals is the customs oﬃce at the border where
travel documents of bus passengers have to be checked.

23

• The behaviour of customers.
Customers may be patient and willing to wait (for a long time). Or customers may
be impatient and leave after a while. For example, in call centers, customers will
hang up when they have to wait too long before an operator is available, and they
possibly try again after a while.
• The service times.
Usually we assume that the service times are independent and identically distributed,
and that they are independent of the interarrival times. For example, the service
times can be deterministic or exponentially distributed. It can also occur that service
times are dependent of the queue length. For example, the processing rates of the
machines in a production system can be increased once the number of jobs waiting
to be processed becomes too large.
• The service discipline.
Customers can be served one by one or in batches. We have many possibilities for
the order in which they enter service. We mention:
– first come first served, i.e. in order of arrival;
– random order;
– last come first served (e.g. in a computer stack or a shunt buffer in a production
line);
– priorities (e.g. rush orders first, shortest processing time first);
– processor sharing (in computers that equally divide their processing power over
all jobs in the system).
• The service capacity.
There may be a single server or a group of servers helping the customers.
• The waiting room.
There can be limitations with respect to the number of customers in the system. For
example, in a data communication network, only finitely many cells can be buffered
in a switch. The determination of good buffer sizes is an important issue in the design
of these networks.
Kendall introduced a shorthand notation to characterize a range of these queueing mod-
els. It is a three-part code a/b/c. The first letter specifies the interarrival time distribution
and the second one the service time distribution. For example, for a general distribution
the letter G is used, M for the exponential distribution (M stands for Memoryless) and
D for deterministic times. The third and last letter specifies the number of servers. Some
examples are M/M/1, M/M/c, M/G/1, G/M/1 and M/D/1. The notation can be ex-
tended with an extra letter to cover other queueing models. For example, a system with
exponential interarrival and service times, one server and having waiting room only for N
customers (including the one in service) is abbreviated by the four letter code M/M/1/N .

24

In the basic model, customers arrive one by one and they are always allowed to enter
the system, there is always room, there are no priority rules and customers are served in
order of arrival. It will be explicitly indicated (e.g. by additional letters) when one of these
assumptions does not hold.

3.2 Occupation rate
In a single-server system G/G/1 with arrival rate λ and mean service time E(B) the
amount of work arriving per unit time equals λE(B). The server can handle 1 unit work
per unit time. To avoid that the queue eventually grows to inﬁnity, we have to require that
λE(B) < 1. Without going into details, we note that the mean queue length also explodes
when λE(B) = 1, except in the D/D/1 system, i.e., the system with no randomness at all.
It is common to use the notation

ρ = λE(B).

If ρ < 1, then ρ is called the occupation rate or server utilization, because it is the fraction
of time the server is working.
In a multi-server system G/G/c we have to require that λE(B) < c. Here the occupa-
tion rate per server is ρ = λE(B)/c.

3.3 Performance measures
Relevant performance measures in the analysis of queueing models are:

• The distribution of the waiting time and the sojourn time of a customer. The sojourn
time is the waiting time plus the service time.

• The distribution of the number of customers in the system (including or excluding
the one or those in service).

• The distribution of the amount of work in the system. That is the sum of service times
of the waiting customers and the residual service time of the customer in service.

• The distribution of the busy period of the server. This is a period of time during
which the server is working continuously.

In particular, we are interested in mean performance measures, such as the mean waiting
time and the mean sojourn time.
Now consider the G/G/c queue. Let the random variable L(t) denote the number of
customers in the system at time t, and let Sn denote the sojourn time of the nth customer
in the system. Under the assumption that the occupation rate per server is less than one,
it can be shown that these random variables have a limiting distribution as t → ∞ and
n → ∞. These distributions are independent of the initial condition of the system.

25

Let the random variables L and S have the limiting distributions of L(t) and Sn ,
respectively. So

pk = P (L = k) = lim P (L(t) = k), FS (x) = P (S ≤ x) = n→∞ P (Sn ≤ x).
lim
t→∞

The probability pk can be interpreted as the fraction of time that k customers are in the
system, and FS (x) gives the probability that the sojourn time of an arbitrary customer
entering the system is not greater than x units of time. It further holds with probability
1 that
1 t 1 n
lim L(x)dx = E(L), lim Sk = E(S).
t→∞ t x=0 n→∞ n
k=1

So the long-run average number of customers in the system and the long-run average
sojourn time are equal to E(L) and E(S), respectively. A very useful result for queueing
systems relating E(L) and E(S) is presented in the following section.

3.4 Little’s law
Little’s law gives a very important relation between E(L), the mean number of customers
in the system, E(S), the mean sojourn time and λ, the average number of customers
entering the system per unit time. Little’s law states that

E(L) = λE(S). (3.1)

Here it is assumed that the capacity of the system is sufficient to deal with the customers
(i.e. the number of customers in the system does not grow to infinity).
Intuitively, this result can be understood as follows. Suppose that all customers pay 1
dollar per unit time while in the system. This money can be earned in two ways. The first
possibility is to let pay all customers “continuously” in time. Then the average reward
earned by the system equals E(L) dollar per unit time. The second possibility is to let
customers pay 1 dollar per unit time for their residence in the system when they leave. In
equilibrium, the average number of customers leaving the system per unit time is equal
to the average number of customers entering the system. So the system earns an average
reward of λE(S) dollar per unit time. Obviously, the system earns the same in both cases.
For a rigorous proof, see [17, 25].
To demonstrate the use of Little’s law we consider the basic queueing model in figure
3.1 with one server. For this model we can derive relations between several performance
measures by applying Little’s law to suitably defined (sub)systems. Application of Little’s
law to the system consisting of queue plus server yields relation (3.1). Applying Little’s
law to the queue (excluding the server) yields a relation between the queue length Lq and
the waiting time W , namely

E(Lq ) = λE(W ).

26

Finally, when we apply Little’s law to the server only, we obtain (cf. section 3.2)

ρ = λE(B),

where ρ is the mean number of customers at the server (which is the same as the fraction
of time the server is working) and E(B) the mean service time.

3.5 PASTA property
For queueing systems with Poisson arrivals, so for M/·/· systems, the very special property
holds that arriving customers find on average the same situation in the queueing system
as an outside observer looking at the system at an arbitrary point in time. More precisely,
the fraction of customers finding on arrival the system in some state A is exactly the same
as the fraction of time the system is in state A. This property is only true for Poisson
arrivals.
In general this property is not true. For instance, in a D/D/1 system which is empty
at time 0, and with arrivals at 1, 3, 5, . . . and service times 1, every arriving customer finds
an empty system, whereas the fraction of time the system is empty is 1/2.
This property of Poisson arrivals is called PASTA property, which is the acrynom for
Poisson Arrivals See Time Averages. Intuitively, this property can be explained by the
fact that Poisson arrivals occur completely random in time (see (2.2)). A rigorous proof of
the PASTA property can be found in [31, 32].
In the following chapters we will show that in many queueing models it is possible to
determine mean performance measures, such as E(S) and E(L), directly (i.e. not from
the distribution of these measures) by using the PASTA property and Little’s law. This
powerful approach is called the mean value approach.

27

3.6 Exercises
Exercise 12.
In a gas station there is one gas pump. Cars arrive at the gas station according to a Poisson
proces. The arrival rate is 20 cars per hour. An arriving car ﬁnding n cars at the station
immediately leaves with probability qn = n/4, and joins the queue with probability 1 − qn ,
n = 0, 1, 2, 3, 4. Cars are served in order of arrival. The service time (i.e. the time needed
for pumping and paying) is exponential. The mean service time is 3 minutes.

(i) Determine the stationary distribution of the number of cars at the gas station.

(ii) Determine the mean number of cars at the gas station.

(iii) Determine the mean sojourn time (waiting time plus service time) of cars deciding
to take gas at the station.

(iv) Determine the mean sojourn time and the mean waiting time of all cars arriving at
the gas station.

28

Chapter 4

M/M/1 queue

In this chapter we will analyze the model with exponential interarrival times with mean
1/λ, exponential service times with mean 1/µ and a single server. Customers are served
in order of arrival. We require that
λ
ρ= < 1,
µ
since, otherwise, the queue length will explode (see section 3.2). The quantity ρ is the
fraction of time the server is working. In the following section we will first study the
time-dependent behaviour of this system. After that, we consider the limiting behaviour.

4.1 Time-dependent behaviour
The exponential distribution allows for a very simple description of the state of the system
at time t, namely the number of customers in the system (i.e. the customers waiting in
the queue and the one being served). Neither we do have to remember when the last
customer arrived nor we have to register when the last customer entered service. Since the
exponential distribution is memoryless (see 2.1), this information does not yield a better
prediction of the future.
Let pn (t) denote the probability that at time t there are n customers in the system,
n = 0, 1, . . . Based on property (2.1) we get, for ∆t → 0,

p0 (t + ∆t) = (1 − λ∆t)p0 (t) + µ∆tp1 (t) + o(∆t),
pn (t + ∆t) = λ∆tpn−1 (t) + (1 − (λ + µ)∆t)pn (t) + µ∆tpn+1 (t) + o(∆t),
n = 1, 2, . . .

Hence, by letting ∆t → 0, we obtain the following infinite set of differential equations for
the probabilities pn (t).

p0 (t) = −λp0 (t) + µp1 (t),
(4.1)
pn (t) = λpn−1 (t) − (λ + µ)pn (t) + µpn+1 (t), n = 1, 2, . . .

29

It is difficult to solve these differential equations. An explicit solution for the probabilities
pn (t) can be found in [14] (see p. 77). The expression presented there is an infinite sum
of modified Bessel functions. So already one of the simplest interesting queueing models
leads to a difficult expression for the time-dependent behavior of its state probabilities. For
more general systems we can only expect more complexity. Therefore, in the remainder
we will focus on the limiting or equilibrium behavior of this system, which appears to be
much easier to analyse.

4.2 Limiting behavior
One may show that as t → ∞, then pn (t) → 0 and pn (t) → pn (see e.g. [8]). Hence, from
(4.1) it follows that the limiting or equilibrium probabilities pn satisfy the equations

0 = −λp0 + µp1 , (4.2)
0 = λpn−1 − (λ + µ)pn + µpn+1 , n = 1, 2, . . . (4.3)

Clearly, the probabilities pn also satisfy

∞
pn = 1, (4.4)
n=0

which is called the normalization equation. It is also possible to derive the equations (4.2)
and (4.3) directly from a flow diagram, as shown in figure 4.1.

© © ©

¡ ¢ £ ¤£¤£ ¨§¥
¡ ¦ ¥ ¤¤£
£ £

Figure 4.1: Flow diagram for the M/M/1 model

The arrows indicate possible transitions. The rate at which a transition occurs is λ for
a transition from n to n+1 (an arrival) and µ for a transition from n+1 to n (a departure).
The number of transitions per unit time from n to n + 1, which is also called the flow from
n to n + 1, is equal to pn , the fraction of time the system is in state n, times λ, the rate
at arrivals occur while the system is in state n. The equilibrium equations (4.2) and (4.3)
follow by equating the flow out of state n and the flow into state n.
For this simple model there are many ways to determine the solution of the equations
(4.2)–(4.4). Below we discuss several approaches.

30

4.2.1 Direct approach
The equations (4.3) are a second order recurrence relation with constant coefficients. Its
general solution is of the form

pn = c1 xn + c2 xn ,
1 2 n = 0, 1, 2, . . . (4.5)

where x1 and x2 are roots of the quadratic equation

λ − (λ + µ)x + µx2 = 0.

This equation has two zeros, namely x = 1 and x = λ/µ = ρ. So all solutions to (4.3) are
of the form

pn = c1 + c2 ρn , n = 0, 1, 2, . . .

Equation (4.4), stating that the sum of all probabilities is equal to 1, of course directly
implies that c1 must be equal to 0. That c1 must be equal to 0 also follows from (4.2) by
substituting the solution (4.5) into (4.2).
The coefficient c2 finally follows from the normalization equation (4.4), yielding that
c2 = 1 − ρ. So we can conclude that

pn = (1 − ρ)ρn , n = 0, 1, 2, . . . (4.6)

Apparantly, the equilibrium distribution depends upon λ and µ only through their ratio ρ.

4.2.2 Recursion
One can use (4.2) to express p1 in p0 yielding

p1 = ρp0 .

Substitution of this relation into (4.3) for n = 1 gives

p 2 = ρ2 p 0 .

By substituting the relations above into (4.3) for n = 2 we obtain p3 , and so on. Hence we
can recursively express all probabilities in terms of p0 , yielding

p n = ρn p 0 , n = 0, 1, 2, . . . .

The probability p0 finally follows from the normalization equation (4.4).

31

4.2.3 Generating function approach
The probability generating function of the random variable L, the number of customers in
the system, is given by
∞
PL (z) = pn z n , (4.7)
n=0

which is properly defined for z with |z| ≤ 1. By multiplying the nth equilibrium equation
with z n and then summing the equations over all n, the equilibrium equations for pn can
be transformed into the following single equation for PL (z),
0 = µp0 (1 − z −1 ) + (λz + µz −1 − (λ + µ))PL (z).
The solution of this equation is
∞
p0 1−ρ
PL (z) = = = (1 − ρ)ρn z n , (4.8)
1 − ρz 1 − ρz n=0
where we used that P (1) = 1 to determine p0 = 1 − ρ (cf. section 3.2). Hence, by equating
the coefficients of z n in (4.7) and (4.8) we retrieve the solution (4.6).

4.2.4 Global balance principle
The global balance principle states that for each set of states A, the flow out of set A is
equal to the flow into that set. In fact, the equilibrium equations (4.2)–(4.3) follow by
applying this principle to a single state. But if we apply the balance principle to the set
A = {0, 1, . . . , n − 1} we get the very simple relation
λpn−1 = µpn , n = 1, 2, . . .
Repeated application of this relation yields
p n = ρn p 0 , n = 0, 1, 2, . . .
so that, after normalization, the solution (4.6) follows.

4.3 Mean performance measures
From the equilibrium probabilities we can derive expressions for the mean number of cus-
tomers in the system and the mean time spent in the system. For the first one we get
∞
ρ
E(L) = npn = ,
n=0 1−ρ
and by applying Little’s law,
1/µ
E(S) = . (4.9)
1−ρ

32

If we look at the expressions for E(L) and E(S) we see that both quantities grow to inﬁnity
as ρ approaches unity. The dramatic behavior is caused by the variation in the arrival and
service process. This type of behavior with respect to ρ is characteristic for almost every
queueing system.
In fact, E(L) and E(S) can also be determined directly, i.e. without knowing the
probabilities pn , by combining Little’s law and the PASTA property (see section 3.5).
Based on PASTA we know that the average number of customers in the system seen by an
arriving customer equals E(L) and each of them (also the one in service) has a (residual)
service time with mean 1/µ. The customer further has to wait for its own service time.
Hence
1 1
E(S) = E(L) + .
µ µ
This relation is known as the arrival relation. Together with
E(L) = λE(S)
we ﬁnd expression (4.9). This approach is called the mean value approach.
The mean number of customers in the queue, E(Lq ), can be obtained from E(L) by
subtracting the mean number of customers in service, so
ρ2
E(Lq ) = E(L) − ρ = .
1−ρ
The mean waiting time, E(W ), follows from E(S) by subtracting the mean service time
(or from E(Lq ) by applying Little’s law). This yields
ρ/µ
E(W ) = E(S) − 1/µ = .
1−ρ

4.4 Distribution of the sojourn time and the waiting
time
It is also possible to derive the distribution of the sojourn time. Denote by La the number of
customers in the system just before the arrival of a customer and let Bk be the service time
of the kth customer. Of course, the customer in service has a residual service time instead
of an ordinary service time. But these are the same, since the exponential service time
distribution is memoryless. So the random variables Bk are independent and exponentially
distributed with mean 1/µ. Then we have
La +1
S= Bk . (4.10)
k=1

By conditioning on La and using that La and Bk are independent it follows that
La +1 ∞ n+1
P (S t) = P ( Bk t) = P( Bk t)P (La = n). (4.11)
k=1 n=0 k=1

33

The problem is to find the probability that an arriving customer finds n customers in the
system. PASTA states that the fraction of customers finding on arrival n customers in the
system is equal to the fraction of time there are n customers in the system, so
P (La = n) = pn = (1 − ρ)ρn . (4.12)
n+1
Substituting (4.12) in (4.11) and using that k=1 Bk is Erlang-(n + 1) distributed, yields
(cf. exercise 2)
∞ n
(µt)k −µt
P (S t) = e (1 − ρ)ρn
n=0 k=0 k!
∞ ∞
(µt)k −µt
= e (1 − ρ)ρn
k=0 n=k k!
∞
(µρt)k −µt
= e
k=0 k!
= e−µ(1−ρ)t , t ≥ 0. (4.13)
Hence, S is exponentially distributed with parameter µ(1 − ρ). This result can also be
obtained via the use of transforms. From (4.10) it follows, by conditioning on La , that
S(s) = E(e−sS )
∞
= P (La = n)E(e−s(B1 +...+Bn+1 ) )
n=0
∞
= (1 − ρ)ρn E(e−sB1 ) · · · E(e−sBn+1 ).
n=0

Since Bk is exponentially distributed with parameter µ, we have (see subsection 2.4.3)
µ
E(e−sBk ) = ,
µ+s
so
∞ n+1
n µ µ(1 − ρ)
S(s) = (1 − ρ)ρ = ,
n=0 µ+s µ(1 − ρ) + s
from which we can conclude that S is an exponential random variable with parameter
µ(1 − ρ).
To find the distribution of the waiting time W , note that S = W +B, where the random
variable B is the service time. Since W and B are independent, it follows that
µ
S(s) = W (s) · B(s) = W (s) · .
µ+s
and thus,
(1 − ρ)(µ + s) µ(1 − ρ)
W (s) = = (1 − ρ) · 1 + ρ · .
µ(1 − ρ) + s µ(1 − ρ) + s

34

From the transform of W we conclude (see subsection 2.3) that W is with probability
(1 − ρ) equal to zero, and with probability ρ equal to an exponential random variable with
parameter µ(1 − ρ). Hence

P (W t) = ρe−µ(1−ρ)t , t ≥ 0. (4.14)

The distribution of W can, of course, also be obtained along the same lines as (4.13).
Note that
P (W t)
P (W t|W 0) = = e−µ(1−ρ)t ,
P (W 0)
so the conditional waiting time W |W 0 is exponentially distributed with parameter
µ(1 − ρ).
In table 4.1 we list for increasing values of ρ the mean waiting time and some waiting
time probabilities. From these results we see that randomness in the arrival and service
process leads to (long) waiting times and the waiting times explode as the server utilization
tends to one.

ρ E(W ) P (W t)
t 5 10 20
0.5 1 0.04 0.00 0.00
0.8 4 0.29 0.11 0.02
0.9 9 0.55 0.33 0.12
0.95 19 0.74 0.58 0.35

Table 4.1: Performance characteristics for the M/M/1 with mean service time 1

Remark 4.4.1 (PASTA property)
For the present model we can also derive relation (4.12) directly from the flow diagram
4.1. Namely, the average number of customers per unit time finding on arrival n customers
in the system is equal to λpn . Dividing this number by the average number of customers
arriving per unit time gives the desired fraction, so
λpn
P (La = n) = = pn .
λ

4.5 Priorities
In this section we consider an M/M/1 system serving different types of customers. To keep
it simple we suppose that there are two types only, type 1 and 2 say, but the analysis can
easily be extended the situation with more types of customers (see also chapter 9). Type 1
and type 2 customers arrive according to independent Poisson processes with rate λ1 , and

35

λ2 respectively. The service times of all customers are exponentially distributed with the
same mean 1/µ. We assume that
ρ1 + ρ2 1,
where ρi = λi /µ, i.e. the occupation rate due to type i customers. Type 1 customers are
treated with priority over type 2 jobs. In the following subsections we will consider two
priority rules, preemptive-resume priority and non-preemptive priority.

4.5.1 Preemptive-resume priority
In the preemptive resume priority rule, type 1 customers have absolute priority over type
2 jobs. Absolute priority means that when a type 2 customer is in service and a type 1
customer arrives, the type 2 service is interrupted and the server proceeds with the type 1
customer. Once there are no more type 1 customers in the system, the server resumes the
service of the type 2 customer at the point where it was interrupted.
Let the random variable Li denote the number of type i customers in the system and
Si the sojourn time of a type i customer. Below we will determine E(Li ) and E(Si ) for
i = 1, 2.
For type 1 customers the type 2 customers do not exist. Hence we immediately have
1/µ ρ1
E(S1 ) = , E(L1 ) = . (4.15)
1 − ρ1 1 − ρ1
Since the (residual) service times of all customers are exponentially distributed with the
same mean, the total number of customers in the system does not depend on the order in
which the customers are served. So this number is the same as in the system where all
customers are served in order of arrival. Hence,
ρ1 + ρ2
E(L1 ) + E(L2 ) = , (4.16)
1 − ρ1 − ρ2
and thus, inserting (4.15),
ρ1 + ρ2 ρ1 ρ2
E(L2 ) = − = ,
1 − ρ1 − ρ2 1 − ρ1 (1 − ρ1 )(1 − ρ1 − ρ2 )
and applying Little’s law,
E(L2 ) 1/µ
E(S2 ) = = .
λ2 (1 − ρ1 )(1 − ρ1 − ρ2 )
Example 4.5.1 For λ1 = 0.2, λ2 = 0.6 and µ = 1, we ﬁnd in case all customers are
treated in order of arrival,
1
E(S) = = 5,
1 − 0.8
and in case type 1 customers have absolute priority over type 2 jobs,
1 1
E(S1 ) = = 1.25, E(S2 ) = = 6.25.
1 − 0.2 (1 − 0.2)(1 − 0.8)

36

4.5.2 Non-preemptive priority
We now consider the situation that type 1 customers have nearly absolute priority over
type 2 jobs. The difference with the previous rule is that type 1 customers are not allowed
to interrupt the service of a type 2 customers. This priority rule is therefore called non-
preemptive.
For the mean sojourn time of type 1 customers we find
1 1 1
E(S1 ) = E(L1 ) + + ρ2 .
µ µ µ
The last term reflects that when an arriving type 1 customer finds a type 2 customer
in service, he has to wait until the service of this type 2 customer has been completed.
According to PASTA the probability that he finds a type 2 customer in service is equal
to the fraction of time the server spends on type 2 customers, which is ρ2 . Together with
Little’s law,
E(L1 ) = λ1 E(S1 ),
we obtain
(1 + ρ2 )/µ (1 + ρ2 )ρ1
E(S1 ) = , E(L1 ) = .
1 − ρ1 1 − ρ1
For type 2 customers it follows from (4.16) that
(1 − ρ1 (1 − ρ1 − ρ2 ))ρ2
E(L2 ) = ,
(1 − ρ1 )(1 − ρ1 − ρ2 )
and applying Little’s law,
(1 − ρ1 (1 − ρ1 − ρ2 ))/µ
E(S2 ) = .
(1 − ρ1 )(1 − ρ1 − ρ2 )

Example 4.5.2 For λ1 = 0.2, λ2 = 0.6 and µ = 1, we get
1 + 0.6 1 − 0.2(1 − 0.8)
E(S1 ) = = 2, E(S2 ) = = 6.
1 − 0.2 (1 − 0.2)(1 − 0.8)

4.6 Busy period
In a servers life we can distinguish cycles. A cycle is the time that elapses between two
consecutive arrivals finding an empty system. Clearly, a cycle starts with a busy period BP
during which the server is helping customers, followed by an idle period IP during which
the system is empty.
Due to the memoryless property of the exponential distribution (see subsection 2.4.3),
an idle period IP is exponentially distributed with mean 1/λ. In the following subsections
we determine the mean and the distribution of a busy period BP .

37

4.6.1 Mean busy period
It is clear that the mean busy period divided by the mean cycle length is equal to the
fraction of time the server is working, so
E(BP ) E(BP )
= = ρ.
E(BP ) + E(IP ) E(BP ) + 1/λ
Hence,
1/µ
E(BP ) = .
1−ρ

4.6.2 Distribution of the busy period
Let the random variable Cn be the time till the system is empty again if there are now n
customers present in the system. Clearly, C1 is the length of a busy period, since a busy
period starts when the first customer after an idle period arrives and it ends when the
system is empty again. The random variables Cn satisfy the following recursion relation.
Suppose there are n( 0) customers in the system. Then the next event occurs after an
exponential time with parameter λ + µ: with probability λ/(λ + µ) a new customer arrives,
and with probability µ/(λ + µ) service is completed and a customer leaves the system.
Hence, for n = 1, 2, . . .,
Cn+1 with probability λ/(λ + µ),
Cn = X + (4.17)
Cn−1 with probability µ/(λ + µ),
where X is an exponential random variable with parameter λ + µ. From this relation we
get for the Laplace-Stieltjes transform Cn (s) of Cn that
λ+µ λ µ
Cn (s) = Cn+1 (s) + Cn−1 (s) ,
λ+µ+s λ+µ λ+µ
and thus, after rewriting,
(λ + µ + s)Cn (s) = λCn+1 (s) + µCn−1 (s), n = 1, 2, . . .
For fixed s this equation is a very similar to (4.3). Its general solution is
Cn (s) = c1 xn (s) + c2 xn (s),
1 2 n = 0, 1, 2, . . .
where x1 (s) and x2 (s) are the roots of the quadratic equation
(λ + µ + s)x = λx2 + µ,
satisfying 0 x1 (s) ≤ 1 x2 (s). Since 0 ≤ Cn (s) ≤ 1 it follows that c2 = 0. The
coefficient c1 follows from the fact that C0 = 0 and hence C0 (s) = 1, yielding c1 = 1.
Hence we obtain
Cn (s) = xn (s),
1

38

and in particular, for the Laplace-Stieltjes transform BP (s) of the busy period BP , we
find
1
BP (s) = C1 (s) = x1 (s) = λ+µ+s− (λ + µ + s)2 − 4λµ .
2λ
By inverting this transform (see e.g. [1]) we get for the density fBP (t) of BP ,
1
fBP (t) = √ e−(λ+µ)t I1 (2t λµ), t 0,
t ρ

where I1 (·) denotes the modified Bessel function of the first kind of order one, i.e.
∞
(x/2)2k+1
I1 (x) = .
k=0 k!(k + 1)!

In table 4.2 we list for some values of ρ the probability P (BP t) for a number of t
values. If you think of the situation that 1/µ is one hour, then 10% of the busy periods
lasts longer than 2 days (16 hours) and 5% percent even longer than 1 week, when ρ = 0.9.
Since the mean busy period is 10 hours in this case, it is not unlikely that in a month time
a busy period longer than a week occurs.

ρ P (BP t)
t 1 2 4 8 16 40 80
0.8 0.50 0.34 0.22 0.13 0.07 0.02 0.01
0.9 0.51 0.36 0.25 0.16 0.10 0.05 0.03
0.95 0.52 0.37 0.26 0.18 0.12 0.07 0.04

Table 4.2: Probabilities for the busy period duration for the M/M/1 with mean service
time equal to 1

4.7 Java applet
For the performance evaluation of the M/M/1 queue a JAVA applet is avalaible on the
World Wide Web. The link to this applet is http://www.win.tue.nl/cow/Q2. The applet
can be used to evaluate the mean value as well as the distribution of, e.g., the waiting time
and the number of customers in the system.

39

4.8 Exercises
Exercise 13. (bulk arrivals)
In a work station orders arrive according to a Poisson arrival process with arrival rate λ.
An order consists of N independent jobs. The distribution of N is given by

P (N = k) = (1 − p)pk−1

with k = 1, 2, . . . and 0 ≤ p 1. Each job requires an exponentially distributed amount
of processing time with mean 1/µ.

(i) Derive the distribution of the total processing time of an order.

(ii) Determine the distribution of the number of orders in the system.

Exercise 14. (variable production rate)
Consider a work station where jobs arrive according to a Poisson process with arrival rate
λ. The jobs have an exponentially distributed service time with mean 1/µ. So the service
completion rate (the rate at which jobs depart from the system) is equal to µ.
If the queue length drops below the threshold QL the service completion rate is lowered to
µL . If the queue length reaches QH , where QH ≥ QL , the service rate is increased to µH .
(L stands for low, H for high.)
Determine the queue length distribution and the mean time spent in the system.
Exercise 15.
A repair man ﬁxes broken televisions. The repair time is exponentially distributed with
a mean of 30 minutes. Broken televisions arrive at his repair shop according to a Poisson
stream, on average 10 broken televisions per day (8 hours).

(i) What is the fraction of time that the repair man has no work to do?

(ii) How many televisions are, on average, at his repair shop?

(iii) What is the mean throughput time (waiting time plus repair time) of a television?

Exercise 16.
In a gas station there is one gas pump. Cars arrive at the gas station according to a Poisson
process. The arrival rate is 20 cars per hour. Cars are served in order of arrival. The service
time (i.e. the time needed for pumping and paying) is exponentially distributed. The mean
service time is 2 minutes.

(i) Determine the distribution, mean and variance of the number of cars at the gas
station.

(ii) Determine the distribution of the sojourn time and the waiting time.

(iii) What is the fraction of cars that has to wait longer than 2 minutes?

40

An arriving car ﬁnding 2 cars at the station immediately leaves.

(iv) Determine the distribution, mean and variance of the number of cars at the gas
station.

(v) Determine the mean sojourn time and the mean waiting time of all cars (including
the ones that immediately leave the gas station).

Exercise 17.
A gas station has two pumps, one for gas and the other for LPG. For each pump customers
arrive according to a Poisson proces. On average 20 customers per hour for gas and 5
customers for LPG. The service times are exponential. For both pumps the mean service
time is 2 minutes.

(i) Determine the distribution of the number of customers at the gas pump, and at the
LPG pump.

(ii) Determine the distribution of the total number of customers at the gas station.

Exercise 18.
Consider an M/M/1 queue with two types of customers. The mean service time of all
customers is 5 minutes. The arrival rate of type 1 customers is 4 customers per hour and
for type 2 customers it is 5 customers per hour. Type 1 customers are treated with priority
over type 2 customers.

(i) Determine the mean sojourn time of type 1 and 2 customers under the preemptive-
resume priority rule.

(ii) Determine the mean sojourn time of type 1 and 2 customers under the non-preemptive
priority rule.

Exercise 19.
Consider an M/M/1 queue with an arrival rate of 60 customers per hour and a mean
service time of 45 seconds. A period during which there are 5 or more customers in the
system is called crowded, when there are less than 5 customers it is quiet. What is the
mean number of crowded periods per day (8 hours) and how long do they last on average?
Exercise 20.
Consider a machine where jobs arrive according to a Poisson stream with a rate of 20 jobs
per hour. The processing times are exponentially distributd with a mean of 1/µ hours.
The processing cost is 16µ dollar per hour, and the waiting cost is 20 dollar per order per
hour.
Determine the processing speed µ minimizing the average cost per hour.

41

Chapter 5

M/M/c queue

In this chapter we will analyze the model with exponential interarrival times with mean
1/λ, exponential service times with mean 1/µ and c parallel identical servers. Customers
are served in order of arrival. We suppose that the occupation rate per server,
λ
ρ= ,
cµ
is smaller than one.

5.1 Equilibrium probabilities
The state of the system is completely characterized by the number of customers in the
system. Let pn denote the equilibrium probability that there are n customers in the system.
Similar as for the M/M/1 we can derive the equilibrium equations for the probabilities pn
from the flow diagram shown in figure 5.1.
¢ ¢ ¢ ¢ ¢

¡ ¥¥¤
¤ ¤ ©§
¨ ¡ § ¥¥¤
¤ ¤ ¨ ¡ ¥¥¤
¤ ¤

£ £ ¦ £ § £ § £ §

Figure 5.1: Flow diagram for the M/M/c model

Instead of equating the flow into and out of a single state n, we get simpler equations
by equating the flow out of and into the set of states {0, 1, . . . , n − 1}. This amounts to
equating the flow between the two neighboring states n − 1 and n yielding
λpn−1 = min(n, c)µpn , n = 1, 2, . . .
Iterating gives
(cρ)n
pn = p0 , n = 0, . . . , c
n!

43

and
c
n n (cρ)
pc+n = ρ pc = ρ p0 , n = 0, 1, 2, . . .
c!
The probability p0 follows from normalization, yielding
c−1 −1
(cρ)n (cρ)c 1
p0 = + · .
n=0 n! c! 1−ρ

An important quantity is the probability that a job has to wait. Denote this probability
by ΠW . It is usually referred to as the delay probability. By PASTA it follows that

ΠW = pc + pc+1 + pc+2 + · · ·
pc
=
1−ρ
c−1 −1
(cρ)c (cρ)n (cρ)c
= (1 − ρ) + . (5.1)
c! n=0 n! c!

Remark 5.1.1 (Computation of ΠW )
It will be clear that the computation of ΠW by using (5.1) leads to numerical problems
when c is large (due to the terms (cρ)c /c!). In remark 11.3.2 we will formulate a numerically
stable procedure to compute ΠW .

5.2 Mean queue length and mean waiting time
From the equilibrium probabilities we directly obtain for the mean queue length,
∞
E(Lq ) = npc+n
n=0
pc ∞
= n(1 − ρ)ρn
1 − ρ n=0
ρ
= ΠW · , (5.2)
1−ρ
and then from Little’s law,
1 1
E(W ) = ΠW · · . (5.3)
1 − ρ cµ
These formulas for E(Lq ) and E(W ) can also be found by using the mean value technique.
If not all servers are busy on arrival the waiting time is zero. If all servers are busy and
there are zero or more customers waiting, then a new arriving customers ﬁrst has to wait
until the ﬁrst departure and then continues to wait for as many departures as there were
customers waiting upon arrival. An interdeparture time is the minimum of c exponential

44

(residual) service times with mean 1/µ, and thus it is exponential with mean 1/cµ (see
exercise 1). So we obtain

1 1
E(W ) = ΠW + E(Lq ) .
cµ cµ

Together with Little’s law we retrieve the formulas (5.2)–(5.3). Table 5.1 lists the delay
probability and the mean waiting time in an M/M/c with mean service time 1 for ρ = 0.9.

c ΠW E(W )
1 0.90 9.00
2 0.85 4.26
5 0.76 1.53
10 0.67 0.67
20 0.55 0.28

Table 5.1: Performance characteristics for the M/M/c with µ = 1 and ρ = 0.9

We see that the delay probability slowly decreases as c increases. The mean waiting time
however decreases fast (a little faster than 1/c). One can also look somewhat differently at
the performance of the system. We do not look at the occupation rate of a machine, but at
the average number of idle machines. Let us call this the surplus capacity. Table 5.2 shows
for fixed surplus capacity (instead of for fixed occupation rate as in the previous table) and
c varying from 1 to 20 the mean waiting time and the mean number of customers in the
system.

c ρ E(W ) E(L)
1 0.90 9.00 9
2 0.95 9.26 19
5 0.98 9.50 51
10 0.99 9.64 105
20 0.995 9.74 214

Table 5.2: Performance characteristics for the M/M/c with µ = 1 and a fixed surplus
capacity of 0.1 server

Although the mean number of customers in the system sharply increases, the mean
waiting time remains nearly constant.

45

5.3 Distribution of the waiting time and the sojourn
time
The derivation of the distribution of the waiting time is very similar to the one in section
4.4 for the M/M/1. By conditioning on the state seen on arrival we obtain
∞ n+1
P (W t) = P( Dk t)pc+n ,
n=0 k=1
where Dk is the kth interdeparture time. Clearly, the random variables Dk are independent
and exponentially distributed with mean 1/cµ. Analogously to (4.13) we ﬁnd
∞ n
(cµt)k −cµt n
P (W t) = e pc ρ
n=0 k=0 k!
∞ ∞
(cµt)k −cµt n
= e pc ρ
k=0 n=k k!
pc ∞ (cµρt)k −cµt
= e
1 − ρ k=0 k!
= ΠW e−cµ(1−ρ)t , t ≥ 0.
This yields for the conditional waiting time,
P (W t)
P (W t|W 0) = = e−cµ(1−ρ)t , t ≥ 0.
P (W 0)
Hence, the conditional waiting time W |W 0 is exponentially distributed with parameter
cµ(1 − ρ). To determine the distribution of the sojourn time we condition on the length of
the service time, so
P (S t) = P (W + B t)
∞
= P (W + x t)µe−µx dx
x=0
t ∞
= P (W t − x)µe−µx dx + µe−µx dx
x=0 x=t
t
= ΠW e−cµ(1−ρ)(t−x) µe−µx dx + e−µt
x=0
ΠW
= e−cµ(1−ρ)t − e−µt + e−µt
1 − c(1 − ρ)
ΠW ΠW
= e−cµ(1−ρ)t + 1 − e−µt .
1 − c(1 − ρ) 1 − c(1 − ρ)

5.4 Java applet
There is also a JAVA applet is avalaible for the performance evaluation of the M/M/c
queue. The WWW-link to this applet is http://www.win.tue.nl/cow/Q2.

46

5.5 Exercises
Exercise 21. (a fast and a slow machine)
Consider two parallel machines with a common buﬀer where jobs arrive according to a
Poisson stream with rate λ. The processing times are exponentially distributed with mean
1/µ1 on machine 1 and 1/µ2 on machine 2 (µ1 µ2 ). Jobs are processed in order of arrival.
A job arriving when both machines are idle is assigned to the fast machine. We assume
that
λ
ρ=
µ1 + µ2
is less than one.
(i) Determine the distribution of the number of jobs in the system.

(ii) Use this distribution to derive the mean number of jobs in the system.

(iii) When is it better to not use the slower machine at all?

(iv) Calculate for the following two cases the mean number of jobs in the system with
and without the slow machine.

(a) λ = 2, µ1 = 5, µ2 = 1;
(b) λ = 3, µ1 = 5, µ2 = 1.

Note: In [21] it is shown that one should not remove the slow machine if r 0.5 where
r = µ2 /µ1 . When 0 ≤ r 0.5 the slow machine should be removed (and the resulting
system is stable) whenever ρ ≤ ρc , where

2 + r2 − (2 + r2 )2 + 4(1 + r2 )(2r − 1)(1 + r)
ρc = .
2(1 + r2 )

Exercise 22.
One is planning to build new telephone boxes near the railway station. The question is
how many boxes are needed. Measurements showed that approximately 80 persons per
hour want to make a phone call. The duration of a call is approximately exponentially
distributed with mean 1 minute. How many boxes are needed such that the mean waiting
time is less than 2 minutes?
Exercise 23.
An insurance company has a call center handling questions of customers. Nearly 40 calls per
hour have to be handled. The time needed to help a customer is exponentially distributed
with mean 3 minutes. How many operators are needed such that only 5% of the customers
has to wait longer than 2 minutes?
Exercise 24.
In a dairy barn there are two water troughs (i.e. drinking places). From each trough only

47

one cow can drink at the same time. When both troughs are occupied new arriving cows
wait patiently for their turn. It takes an exponential time to drink with mean 3 minutes.
Cows arrive at the water troughs according to a Poisson process with rate 20 cows per
hour.

(i) Determine the probability that there are i cows at the water troughs (waiting or
drinking), i = 0, 1, 2, . . .

(ii) Determine the mean number of cows waiting at the troughs and the mean waiting
time.

(iii) What is the fraction of cows ﬁnding both troughs occupied on arrival?

(iv) How many troughs are needed such that at most 10% of the cows ﬁnd all troughs
occupied on arrival?

Exercise 25.
A computer consists of three processors. Their main task is to execute jobs from users.
These jobs arrive according to a Poisson process with rate 15 jobs per minute. The execu-
tion time is exponentially distributed with mean 10 seconds. When a processor completes
a job and there are no other jobs waiting to be executed, the processor starts to execute
maintenance jobs. These jobs are always available and they take an exponential time with
mean 5 seconds. But as soon as a job from a user arrives, the processor interrupts the
execution of the maintenance job and starts to execute the new job. The execution of the
maintenance job will be resumed later (at the point where it was interrupted).

(i) What is the mean number of processors busy with executing jobs from users?

(ii) How many maintenance jobs are on average completed per minute?

(iii) What is the probability that a job from a user has to wait?

(iv) Determine the mean waiting time of a job from a user.

48

Chapter 6

M/Er /1 queue

Before analyzing the M/G/1 queue, we first study the M/Er /1 queue. The Erlang dis-
tribution can be used to model service times with a low coefficient of variation (less than
one), but it can also arise naturally. For instance, if a job has to pass, stage by stage,
through a series of r independent production stages, where each stage takes a exponen-
tially distributed time. The analysis of the M/Er /1 queue is similar to that of the M/M/1
queue.
We consider a single-server queue. Customers arrive according to a Poisson process with
rate λ and they are treated in order of arrival. The service times are Erlang-r distributed
with mean r/µ (see subsection 2.4.4). For stability we require that the occupation rate
r
ρ=λ· (6.1)
µ
is less than one. In the following section we will explain that there are two ways in which
one can describe the state of the system.

6.1 Two alternative state descriptions
The natural way to describe the state of a nonempty system is by the pair (k, l) where k
denotes the number of customers in the system and l the remaining number of service phases
of the customer in service. Clearly this is a two-dimensional description. An alternative
way to describe the state is by counting the total number of uncompleted phases of work
in the system. Clearly, there is a one to one correspondence between this number and
the pair (k, l). The number of uncompleted phases of work in the system is equal to the
number (k − 1)r + l (for the customer in service we have l phases of work instead of r).
From here on we will work with the one-dimensional phase description.

6.2 Equilibrium distribution
For the one-dimensional phase description we get the flow diagram of figure 6.1.

49

¦ ¦

¡ ¢ ¤¤£
£ £ § ¨ ©§ ¡ ¤¤£
£ £

¥ ¥ ¥

Figure 6.1: One-dimensional flow diagram for the M/Er /1 model

Let pn be the equilibrium probability of n phases work in the system. By equating the
flow out of state n and the flow into state n we obtain the following set of equilibrium
equations for pn .

p0 λ = p1 µ, (6.2)
pn (λ + µ) = pn+1 µ, n = 1, . . . , r − 1, (6.3)
pn (λ + µ) = pn−r λ + pn+1 µ, n = r, r + 1, r + 2, . . . (6.4)

These equations may be solved as follows. We first look for solutions of (6.4) of the form

pn = xn , n = 0, 1, 2, . . . (6.5)

and then we construct a linear combination of these solutions also satisfying the boundary
equations (6.2)–(6.3) and the normalization equation
∞
pn = 1.
n=0

An alternative solution approach is based on generating functions (see exercise 27).
Substitution of (6.5) into (6.4) and then dividing by the common power xn−r yields the
polynomial equation

(λ + µ)xr = λ + µxr+1 . (6.6)

One root is x = 1, but this one is not useful, since we must be able to normalize the
solution of the equilibrium equations. Provided condition (6.1) holds, it can be shown that
equation (6.6) has exactly r distinct roots x with |x| 1, say x1 , . . . , xr (see exercise 26).
We now consider the linear combination
r
pn = ck xn ,
k n = 0, 1, 2, . . . (6.7)
k=1

For each choice of the coefficients ck this linear combination satisfies (6.4). This freedom is
used to also satisfy the equations (6.2)–(6.3) and the normalization equation. Note that,
since the equilibrium equations are dependent, equation (6.2) (or one of the equations in
(6.3)) may be omitted. Substitution of (6.7) into these equations yields a set of r linear

50

Queueing 2

More Related Content

Queueing 2