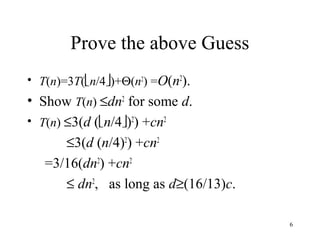Recurrence theorem

1
Asymptotic Efficiency of Recurrences
• Find the asymptotic bounds of recursive
equations.
– Substitution method
• domain transformation
• Changing variable
– Recursive tree method
– Master method (master theorem)
• Provides bounds for: T(n) = aT(n/b)+f(n) where
– a ≥ 1 (the number of subproblems).
– b>1, (n/b is the size of each subproblem).
– f(n) is a given function.

2
Recurrences
• MERGE-SORT
– Contains details:
• T(n) = Θ(1) if n=1
T(n/2)+ T(n/2)+ Θ(n) if n>1
• Ignore details, T(n) = 2T(n/2)+ Θ(n).
– T(n) = Θ(1) if n=1
2T(n/2)+ Θ(n) if n>1

3
The Recursion-tree Method
• Idea:
– Each node represents the cost of a single subproblem.
– Sum up the costs with each level to get level cost.
– Sum up all the level costs to get total cost.
• Particularly suitable for divide-and-conquer
recurrence.
• Best used to generate a good guess, tolerating
“sloppiness”.
• If trying carefully to draw the recursion-tree and
compute cost, then used as direct proof.

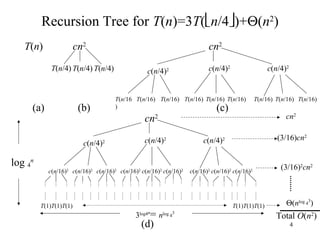
4
Recursion Tree for T(n)=3T(n/4)+Θ(n2
)
T(n)
(a)
cn2
T(n/4) T(n/4) T(n/4)
(b)
cn2
c(n/4)2 c(n/4)2
c(n/4)2
T(n/16) T(n/16) T(n/16)T(n/16)T(n/16)T(n/16
)
T(n/16) T(n/16) T(n/16)
(c)
cn2
c(n/4)2 c(n/4)2
c(n/4)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
c(n/16)2
cn2
(3/16)cn2
(3/16)2
cn2
T(1)T(1) T(1)T(1) T(1)T(1) Θ(nlog 4
3
)
3log4n
= nlog 4
3
Total O(n2
)
log 4
n
(d)

5
Solution to T(n)=3T(n/4)+Θ(n2
)
• The height is log 4
n,
• #leaf nodes = 3log4
n
= nlog4
3
. Leaf node cost: T(1).
• Total cost T(n)=cn2
+(3/16) cn2
+(3/16)2
cn2
+
⋅⋅⋅ +(3/16)log4
n-1
cn2
+ Θ(nlog4
3
)
=(1+3/16+(3/16)2
+ ⋅⋅⋅ +(3/16)log4
n-1
) cn2
+ Θ(nlog4
3
)
<(1+3/16+(3/16)2
+ ⋅⋅⋅ +(3/16)m
+ ⋅⋅⋅)
cn2
+ Θ(nlog4
3
)
=(1/(1-3/16)) cn2
+ Θ(nlog4
3
)
=16/13cn2
+ Θ(nlog4
3
)
=O(n2
).

6
Prove the above Guess
• T(n)=3T(n/4)+Θ(n2
) =O(n2
).
• Show T(n) ≤dn2
for some d.
• T(n) ≤3(d (n/4)2
) +cn2
≤3(d (n/4)2
) +cn2
=3/16(dn2
) +cn2
≤ dn2
, as long as d≥(16/13)c.

7
One more example
• T(n)=T(n/3)+ T(2n/3)+O(n).
• Construct its recursive tree (
Figure 4.2, page 71).
• T(n)=O(cnlg3/2
n) = O(nlg n).
• Prove T(n) ≤ dnlg n.

8
Recursion Tree of T(n)=T(n/3)+ T(2n/3)+O(n)

Recurrence theorem

More Related Content

Recurrence theorem