RSA暗号運用でやってはいけない n のこと #ssmjp
- 2. sonickun (@y_hag) 大学院生(4月から就職) #ssmjpで過去に2度発表しました 「ダークネットの話」 #ssmjp 2015/02 http://www.slideshare.net/sonickun/ss-44926963 「進化するWebトラッキングの話」 #ssmjp 2015/07 http://www.slideshare.net/sonickun/web-51132299 自己紹介
- 4. Ron Rivest、Adi Shamir、Leonard Adleman によって 発明された公開鍵暗号方式 桁数が大きな合成数の素因数分解が困難であること を安全性の根拠としている RSA暗号とは 平文 暗号文 公開鍵 秘密鍵
- 5. 鍵生成 素数𝒑, 𝒒を選ぶ 𝒏 = 𝒑 ∗ 𝒒, 𝝋(𝒏) = (𝒑 − 𝟏) ∗ (𝒒 − 𝟏) 𝝋(𝒏) と互いに素となるような 𝒆 を選ぶ 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) となる最小の 𝒅 を求める 𝒏, 𝒆 を公開鍵,𝒑, 𝒒, 𝒅 を秘密鍵とする RSA暗号のアルゴリズム 平文 𝒎 暗号文 𝒄 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏
- 8. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 RSA暗号運用でやってはいけない 𝒏 のこと その 1 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 公開鍵 𝒏 のビット数(鍵長)が 小さくてはいけない 𝑛 が小さいと容易に素因数分解できてしまう 最新の計算機環境では768bitの整数の素因数分解 に成功している (RSA Factoring Challenge) 2017年時点で1024bit以下は非推奨 (NIST)
- 9. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 2 𝒑, 𝒒 の片方が小さい値になってはいけない 𝑛 の大きさが十分であっても、片方の素数が小さい と、𝑛 を小さい素数から順に割っていくと素因数 分解できてしまう
- 10. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 3 近い値の素数 𝒑, 𝒒 を使ってはいけない フェルマー法で素因数分解可能 𝑝, 𝑞 の値が近いと、それらの値は 𝑛 の平方根の周辺 に限定される
- 11. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 素数 𝒑, 𝒒 を有名な素数(メルセンヌ素数など) にしてはいけない 𝟐^𝒏 − 𝟏(𝑛 は自然数)で表される自然数をメルセ ンヌ数といい、そのうち素数のものをメルセンヌ 素数という 現在見つかっているメルセンヌ素数は49個のみ 4
- 12. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 公開鍵 𝒏 の生成時に 同じ素数を使いまわしてはいけない 𝑛 = 𝒑 ∗ 𝑞, 𝑛’ = 𝒑 ∗ 𝑟 のとき、𝑛 と 𝑛’ の公約数を 計算することで 𝑝 が求まる 5
- 13. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 𝒆 の値が小さすぎてはいけない Low Public Exponent Attack が適用可能 𝑒 と 𝑛 が共に小さく( 𝑒 = 3など)、 𝑚^𝑒 < 𝑛 のとき、 𝑐 の 𝑒 乗根を計算することで m が求まる 6
- 14. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 𝒆 の値が大きすぎてはいけない Wiener‘s Attack が適用可能 𝑒 が大きいと相対的に 𝑑 が小さくなることを利用 して 𝑒 と 𝑛 から秘密鍵が求まる 𝑒 の値は 65537 (0x10001) が選ばれるのが一般的 7
- 15. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 同一の平文を異なる 𝒆 で暗号化した 暗号文を与えてはいけない Common Modulus Attack が適用可能 𝑚, 𝑛 が共通で 𝑒 が異なる 𝑒, 𝑐 の組があるとき、 拡張ユークリッド互除法を用いて平文𝑚を計算 できる 8
- 16. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 同一の平文を異なる 𝒏 で暗号化した 暗号文を与えてはいけない Håstad‘s Broadcast Attack が適用可能 同一の 𝑚 を異なる 𝑛 で暗号化した 𝑐 が 𝑒 個 得られ たとき、中国人剰余定理を用いて 𝑚 が求まる 9
- 17. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 任意の暗号文を復号した結果の 偶奇 (下位1bit) を知られてはいけない LSB Decryption Oracle Attack が適用可能 𝑐 に対して 𝑚 の偶奇がわかるとき、二分探索に よって 𝑚 が求まる 10
- 18. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 上位ビットが共通する二つの平文に対する 暗号文を知られてはいけない Franklin-Reiter Related Message Attack が 適用可能 二つの平文 𝑚1, 𝑚2 = 𝑎 ∗ 𝑚1 + 𝑏 と、それぞれの 暗号文が得られるとき、𝑚1を導出可能 11
- 19. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 素数 𝒑 の上位ビットまたは下位ビットが 知られてはいけない Coppersmith‘s Attack が適用可能 Coppersmithの定理を用いて素数 𝑝 の一部の情報 ( 𝑝 のビット数の1/2程度) から 𝑝 を特定できる 12
- 20. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 秘密鍵 𝒅 の下位ビットが知られてはいけない Coppersmith‘s Attack (Partial Key Exposure Attack) が適用可能 Coppersmithの定理を用いて秘密鍵 𝑑 の一部の情報 ( 𝑑 のビット数の1/4程度) から 𝑑 を特定できる 13
- 21. RSA暗号運用でやってはいけない 𝒏 のこと その 𝒏 = 𝒑 ∗ 𝒒, 𝝋 𝒏 = 𝒑 − 𝟏 ∗ 𝒒 − 𝟏 , 𝝋 𝒏 ⊥ 𝒆, 𝒅 ∗ 𝒆 ≡ 𝟏 (𝒎𝒐𝒅 𝝋(𝒏)) 暗号化: 𝒄 = 𝒎^𝒆 𝒎𝒐𝒅 𝒏 復号: 𝒎 = 𝒄^𝒅 𝒎𝒐𝒅 𝒏 平文 𝒎 の上位ビットまたは下位ビットが 知られてはいけない Coppersmith‘s Attack が適用可能 Coppersmithの定理を用いて平文 𝑚 の一部の情報 ( 𝑚 のビット数の 1 − 1/𝑒 程度) から 𝑚 を特定できる 14
- 22. 以上! ※ ホントは他にもあります RSA-CRT Fault Attack 適応的選択暗号文攻撃 Coppersmith's Short Pad Attack Boneh-Durfee Attack 乱数生成器の偏りを利用した攻撃 など…
- 23. 公開鍵 𝒏 のビット数(鍵長)が小さくてはいけない・𝒑, 𝒒 の片方が 小さい値になってはいけない・近い値の素数 𝒑, 𝒒 を使ってはいけ ない・素数 𝒑, 𝒒 を有名な素数(メルセンヌ素数など)にしてはいけ ない・公開鍵 𝒏 の生成時に同じ素数を使いまわしてはいけない・ 𝒆 の値が小さすぎてはいけない・𝒆 の値が大きすぎてはいけない・ 同一の平文を異なる 𝒆 で暗号化した暗号文を与えてはいけない ・同一の平文を異なる 𝒏 で暗号化した暗号文を与えてはいけな い・任意の暗号文を復号した結果の偶奇 (下位1bit) を知られては いけない・上位ビットが共通する二つの平文に対する暗号文を知 られてはいけない・素数 𝒑 の上位ビットまたは下位ビットが知ら れてはいけない・秘密鍵 𝒅 の下位ビットが知られてはいけない・ 平文 𝒎 の上位ビットまたは下位ビットが知られてはいけない RSA暗号運用でやってはいけない 14 のこと
- 24. RSA暗号 の 運用は難しい??
- 25. OpenSSL インターネット上で標準的に利用される暗号プロトコルを 実装したオープンソースのライブラリ 疑似乱数生成器を用いて安全なRSA鍵を生成してくれる OpenSSL で安全な鍵を作ろう コマンド例 秘密鍵の生成 公開鍵の生成 $ openssl genrsa 2048 > private-key.pem $ openssl rsa -pubout < private-key.pem > public-key.pem
- 26. こまめにアップデートを OpenSSLの脆弱性は頻繁に見つかる(2016年で34件*) 少し昔のバージョンではデフォルトの鍵長が短い 疑似乱数生成器の seed (種) は予測不可能なものに UNIX系であれば /dev/random または /dev/urandom EGD (UNIX) やEGADS (UNIX+Windows) などのエントロピー 収集ツール 望ましくない seed 例:時刻、特定のファイル、スクリーン ショット画像、キーストロークなど OpenSSL 使用上の注意点 *Openssl : CVE security vulnerabilities, versions and detailed reports http://www.cvedetails.com/product/383/Openssl-Openssl.html?vendor_id=217
- 28. つくってみた Cryptools - RSA実装+攻撃 Pythonライブラリ https://github.com/sonickun/cryptools CTF暗号問題Writeupまとめ https://github.com/sonickun/ctf-crypto-writeups おまけ
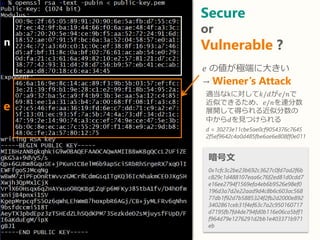
- 31. Secure or Vulnerable ? 暗号文 0x1cfc3c2be23b692c3627c0fd7ad2f6b c829c1d488107eaa6c76f2ed81d0cdd7 e16ee2794f1569efa4eb6b9526e98ef0 196d3a7d2e22aad9d4c8b6c603ac568 77db1f92d7b5885324f2fb2d2000e892 3402861ceb31f4ef63c7a2c950160717 d7195fb7fd4de794fd0b116e06ca5bff1 f964d79e1276291d2bb1e403371b971 eb n e 𝑒 の値が極端に大きい → Wiener’s Attack 適当なkに対して𝑘/𝑑が𝑒/𝑛で 近似できるため、𝑒/𝑛を連分数 展開して得られる近似分数の 中から𝑑を見つけられる d = 30273e11cbe5ae0cf9054376c7645 2f5ef9642c4a0d485fbe6ae6e808ff0e011
- 32. Secure or Vulnerable ?n e 𝑒 の値が極端に大きい → Wiener’s Attack 適当なkに対して𝑘/𝑑が𝑒/𝑛で 近似できるため、𝑒/𝑛を連分数 展開して得られる近似分数の 中から𝑑を見つけられる d = 30273e11cbe5ae0cf9054376c7645 2f5ef9642c4a0d485fbe6ae6e808ff0e011 平文 “Thank you !”