Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
SlideShare a Scribd company logo

第一原理計算と密度汎関数理論

•
•
D
dc1394
1 of 74
@dc1394 2016/2/3 Rev. 1.993 第一原理計算と密度汎関数理論
はじめに  このスライドは最初，第一原理計算と密度汎関数理論を， 「誰にでも」理解できるように，説明する目的で作り始めま した。  しかし残念ながら，著者の不勉強と理論の難解さで，とて も「誰にでも」理解できる内容にはなりませんでした。  また著者自身，密度汎関数理論を完全に理解できていな いので，間違っている部分があるかもしれません。  Richard P. Feynmanが言ったように，「高校生レベルの知識 層に説明して伝えることができなければ，その人は科学を 理解しているとは言えない。」のですが，このスライドが少 しでも皆様の理解の助けになれば幸いです。  なお，著者が特に尊敬している物理学者は，Wikipediaか ら拝借した写真を入れさせて頂きました。
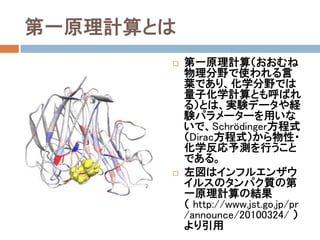
第一原理計算とは  第一原理計算（おおむね物 理分野で使われる言葉であ り，化学分野では量子化学 計算とも呼ばれる）とは，実 験データや経験パラメーター を用いないで，Schrödinger方 程式（Dirac方程式）から物 性・化学反応予測を行うこと である。  左図はインフルエンザウ イルスのタンパク質と，イ ンフルエンザ治療薬のタ ミフルの結合系の第一原 理計算の結果 （ http://www.jst.go.jp/pr/ann ounce/20100324/ より引用）
計算例：ケイ素のバンド分散 第一原理計算の一例 （著者の計算結果）。 ダイアモンド構造のケイ 素について計算を行い， バンド分散を図に示した。 バンドギャップが存在し， 半導体である。
第一原理計算の例  第一原理計算（量子化学計算）によって現在研究 されている対象を幾つか列挙してみる。  HIV，インフルエンザなど難病のメカニズムの解明， 治療薬の開発  光合成，植物の窒素固定のメカニズムの解明  高温超伝導，高効率の太陽電池，燃料電池，蓄 電池に必要な素材・物質…など。  以上のような機構，薬品・素材・物質の構造や合 成法が，コンピュータ上のシミュレーションで，少 なくとも理論上は完全にわかる。  →しかし現状はそうなっていない，なぜか？
第一原理計算の課題  全く近似なしでまともにSchrödinger方程式を解くと， 計算量のオーダーは…見積もった人は（たぶん） いない（Dirac方程式はさらに複雑）。  Schrödinger方程式において，Born-Oppenheimer近 似（後述）の下で，配置間相互作用（Full CI）法を 用いた計算（非常に小さな系を除いて，現在最も 厳密に近い解が得られる計算法）では，計算量は おおむねO(N!)となる（少なめに見積もっても，aを 定数としてO(aN)）。  ここで，Nはだいたい原子の個数と思ってよい（正 確には考慮する軌道の個数）。
第一原理計算の課題  1グラムの水でさえ1023個のオーダーの原子 を含むので，マクロな系については，世界中の スーパーコンピュータを全て用いても，現実的 な時間で結果を得ることは不可能である。  これは，Schrödinger方程式（Dirac方程式）が多 体問題であることに起因する。  Paul A. M. Diracの言葉：「物理の大部分と化学 の全体を数学的に取り扱うために必要な基本 的法則は完全にわかっている。これらの法則 を適用すると複雑すぎて解くことのできない方 程式に行き着いてしまうことだけが困難なので ある。」 Paul A. M. Dirac (1902-1984)
第一原理計算の課題  このスライドの主なテーマである密度汎関数理論でも， 計算量はO(N3)であり，マクロな系の計算を現実的な 時間で行うことは依然不可能である。  計算量が原子数に単に比例する，オーダーN密度汎 関数理論の開発も行われているが，今のところ最先 端の研究でも，地球シミュレータなどのスーパーコン ピュータを用いて，N～104の系が限界（「京」をフルに 用いればN～105，あるいはN～106の系を計算可能 か？）  また，CPU単一コアの性能の向上が鈍化した現在，大 規模計算にはSIMD，マルチスレッド，マルチプロセス， GPGPUなどによる並列化が必要不可欠である。
Schrödinger方程式とは  量子力学の（非相対論的な）基 礎方程式で，1926年にErwin R. J. A. Schrödingerが提出。  単一粒子について，時間に依存 しない定常状態でのSchrödinger 方程式（最も解きやすい表式）は， Erwin R. J. A. Schrödinger (1887-1961)
Dirac方程式とは  原子番号の大きい元素を扱う際は，（特殊）相対論効 果が無視できない→Dirac方程式。  Dirac方程式：Fermi粒子に対する相対論的量子力学 の基礎方程式で，1928年にPaul A. M. Diracが提出。  単一粒子について，時間に依存しない定常状態での Dirac方程式は（pだけベクトルの表記をBoldにした），  この方程式は4成分方程式であり，第一原理計算で は2成分相対論，スカラー相対論などで解く。  非常に難しいのでこのスライドではこれ以上扱いませ ん（著者も完全には理解していません）。
Hartree原子単位系  第一原理計算では，Schrödinger方程式の表式を簡潔 にするために，Hartree原子単位系が使用される （Rydberg原子単位系が使用されることもある）。  この単位系では，長さの単位はBohr半径a0 (1 [a0] = 5.29×10-11 [m]), 質量の単位は電子の質量me, 電荷 は電気素量e, エネルギーはHartree (1 [Hartree] = 4.36×10-18 [J] = 27.2 [eV])を用いる。  この単位系では，Dirac定数ℏと，Coulombポテンシャ ルの比例定数1 / (4πε0)が1となる。  単位を表す記号として，すべて atomic unit の省略形 である a.u. で表すことが多い。
水素原子に対するSchrödinger方程式  最も簡単な水素原子について，定常状態における Schrödinger方程式を以下に示す（以後，Hartree原子 単位系を用いる）。  ここで，  この方程式は（少なくとも見かけ上は）単純であり，ま た解析的に解くことができる（しかし実際に解こうとす ると大変：参考「水素原子におけるシュレーディンガー 方程式の解 – Wikipedia」 http://bit.ly/12nEHqV ）。  この方程式の解から，重要な情報がいくつも得られる。 Coulombポテンシャル電子の運動エネルギーポテンシャル
Born-Oppenheimer近似  一般に第一原理計算では，電子と（原子）核の二 つの粒子の質量の大きな差（水素原子の場合， 電子：核＝1：1837）から，Born-Oppenheimer近似 が用いられる。  この近似により，電子と核の運動を分離できる。  これは，電子が核に相対的に運動している間は， 核が「静止」していると見なすことに相当する。  通常，核の運動については，量子力学と古典的な Newton方程式を併用する（第一原理分子動力学 法，これも難しいのでこのスライドではこれ以上扱 いません）。
ヘリウム原子に対するSchrödinger方程式  次に，Born-Oppenheimer近似の下で，ヘリウム原 子に対するSchrödinger方程式を書いてみる。  この方程式は3次元×2=6次元の偏微分方程式 である（r1とr2は別の次元であることに注意）。  上記の方程式では省略しているが，本当は（電子 の）スピン次元も考えなければならない。 電子1の運動 エネルギー ポテンシャル 電子2の運動 エネルギー ポテンシャル 電子1の Coulombポテン シャル 電子2の Coulombポテン シャル 電子1と電子2間の Coulombポテンシャル →この項が問題
N電子系のSchrödinger方程式  ヘリウム原子の場合には，数値解法で無理矢理 解けなくもない。  しかし一般にN電子系では，3N次元（+スピン次 元）の偏微分方程式を解かなければならない（例 えば，リチウム原子では9次元，ベリリウム原子で は12次元，これにスピン次元が加わる）。  Nが大きくなると，数値解法で無理矢理解こうとす るのは明らかに無謀である。  →何かいい方法はないか？？
Hartree-Fock法  多体問題に対処する一つの方法として，多体問題を 一体問題に帰着（一電子近似）させる，Hartree-Fock 法がある。  この方法は，摂動の高次項を計算することで，系統的 に解の精度を改良できるのが特長であり，化学分野 では一般的に用いられている（例えば，このスライド の三枚目で紹介した図の計算は，実はこの方法に よっている）。  物理分野でも，この方法で得た知見は，Hybrid-GGA などに生かされている。  このスライドでは，この方法についてこれ以上触れな い。多体問題に対処するもう一つの方法については， 以降で詳しく述べる。
密度汎関数理論  粒子（ここでは電子に限る）の存在確率を求めた い場合，3N次元波動関数ψ(r1, r2,..., rN)ではなく， 波動関数の絶対値の2乗である，3次元の電子密 度の関数ρ(r)のみで計算できる（Bornの確率解釈）。  ならば，ρ(r)を用いて他の物理量を求めることもで きるのではないだろうか？  もしそうならば，複雑な3N次元波動関数ではなく， 3次元の電子密度の関数ρ(r)を求めればよい。  このような考えに基づいて，密度汎関数理論 （Density Functional Theory, DFT）が提出された。
Hohenberg-Kohnの第1定理  1964年，HohenbergとKohnは，この 定式化が実際に可能であることを 示した。  Hohenberg-Kohnの第1定理：エネル ギーのゼロ点の取り方を除いて， 基底状態の電子密度ρ(r)から外部 ポテンシャルv(r)が決定される。  これは，基底状態の電子密度ρ(r)と， 外部ポテンシャルv(r)が1対1対応す る，ということを述べている。 Walter Kohn (1923-2016)
Hohenberg-Kohnの第2定理  Hohenberg-Kohnの第2定理：どのような外部ポテ ンシャルv(r)に対しても成り立つ電子密度の汎関 数EHK[ρ]（Hohenberg-Kohnの「普遍的な」エネル ギー汎関数）が存在する。  与えられた外部ポテンシャルの下で，この汎関数 は，基底状態の電子密度ρ0(r)で最小値を与え，こ れは系の基底状態のエネルギーと等しい。  よって，電子密度を変化させて，最小のエネル ギーを与える電子密度を探索すれば，基底状態 の電子密度を求めることができる。
Hohenberg-Kohnの第2定理  要するに，色々な電子密度ρ(r)があり得るが， EHK[ρ]に代入すれば，得られるエネルギーが最小 となるような電子密度が「正解」である。  従って，そのような電子密度ρ0(r)を何とかして探し 出せばよい，と言うことを言っている。
拘束条件付きの最小化  以上の議論をより数学的に定式化すると，全電子 数が一定であるという拘束条件  の下で，EHK[ρ]を最小化すれば，基底状態の電子 密度が求められる，ということになる。すなわち， Lagrangeの未定乗数法を使って，電子密度ρ(r)が 停留条件  を満たすとき，それは「正解」の基底状態の電子 密度であり，一意的に定まる。ここで，μは Lagrangeの乗数（物理的にはFermiエネルギーあ るいは化学ポテンシャル）である。
N表示可能性  ここで，二つの重要な疑問が生まれる。  一つ目の疑問は，「可能な密度全てを表現できる Fermi粒子系に対する，反対称波動関数を作るこ とができるであろうか？」というもので，これは「N 表示可能性」と呼ばれる。  これは「可能」である。  ただし密度にいくつかの制限を課す必要がある。 その制限とは，  である。
v表示可能性  二つ目の疑問は，「（適当な）密度が，ある局所的 外部ポテンシャルv(r)に対する，基底状態の密度 となるようにすることは可能であろうか？」というも ので，これは「v表示可能性」と呼ばれる。  この疑問は，非常に興味深いことに，「不可能」で ある。つまり，どんなv(r)に対しても基底状態の密 度とならない，一見「もっともらしい」密度の多数の 例がある。  N表示可能性はv表示可能性の必要条件となって いる。
Levyの制限付き探索  変分原理において，前ページの議論を考慮すると， その密度ρ(r)がv表示可能かどうかを，その都度確 かめる必要がある，という結論に達する。  しかし，Levyは以下の式，  を用いれば，問題なくHohenberg-Kohnの定理が成 り立ち，多数ある密度ρ(r) の中から，ρ0(r)を探索す ることができる，ということを示した。  これをLevyの制限付き探索と呼ぶ。
Levyの制限付き探索  Levyの制限付き探索の具体的な手順は，以下のよう になる。  まず，密度ρ(r)を固定して，そのような特定のρ(r)を与 える波動関数ψρの組の中で，T + Veeを評価し，その 値を最小化するようなψρを探す。そして，その最小値 をQ[ρ]と定義する。  次に，今度は密度ρ(r)を固定せずに，  における左辺E[ρ]を最小化するようなρを探索する。  つまり，最小化を二段階に分けて行う。
Levyの制限付き探索  この方法によると，v表示可能なρ(r)の領域ではQ[ρ] は， と一致する。  一方，v表示可能な領域外でも，汎関数Q[ρ]が定義で きる。  この汎関数Q[ρ]を用いれば，ρ(r)がv表示可能な領域 にあるかどうかにかかわらず，Hohenberg-Kohnの第2 定理の変分原理が適用可能となる。  これは，以下のように例えることができる。  学校全体で一番背の高い生徒を見つけるのに，全員 を校庭に一列に並ばせる必要はない。単に，各教室 で一番背の高い生徒を校庭に呼び出して，一列に並 べれば良い。
汎関数  Hohenberg-Kohnの定理では，電子密度の「関数」では なく「汎関数」と言っている（その汎関数の表式につい ては何も言っていない）。  通常の関数は，入力は変数x, 出力は数値f(x)である。 しかし汎関数は，入力は関数f, 出力は数値I[f]である。 例えば，  を考えると，Iは関数f(x)の形に応じて値を変えるので， 汎関数である（合成関数とは異なるので注意）。  関数はf(x)と，()の中に変数を書くが，汎関数はI[f]と， []の中に関数を書く。
「普遍的な」汎関数を求めることの難 しさ  「普遍的な」汎関数を見つけるための手段は，多体波 動関数を使ったもとの定義より他には，全く与えられ ていない。  また， 「普遍的な」汎関数のすべての部分は，電子数 の関数として非解析的な振る舞いをするであろう。  従って，そのような「普遍的な」汎関数の明示的な形 を求めることは困難である。  現在でも，「普遍的な」汎関数を求めるべく努力が続 けられているが，現状では近似式が用いられている。  個人的な意見：「普遍的な」汎関数を求めることは不可能に近いと思われる。よ しんば求めることができたとしても，それは非常に複雑で，計算量は結局，3N次 元のSchrödinger方程式を解くのと同じになるのではないだろうか？
局所密度近似（LDA）  「普遍的な」汎関数はわからないので，「同じ密度を 持っている均質で一様な電子ガス」を考える。  このような，「一様な電子ガス」に対する汎関数は，解 析的に求めることができる。  そして，実際に計算したい系も，「一様な電子ガス」の ように「局所的に」振る舞うと仮定する。  これはポテンシャルについて，「汎関数」を「一様な電 子ガス」から求めた結果の，普通の「関数」で近似して しまうことを意味する。  これを局所密度近似（Local Density Approximation, LDA）という。  厳密には上記は間違いであり，相関汎関数（後述）だけは解析的に求めるこ とは不可能である。
注意  以後の局所密度近似（LDA）の導出は難しいので 割愛します。  詳しく知りたい方は，  R.G.パール, W.ヤング 『原子･分子の密度汎関数 法』シュプリンガー・フェアラーク東京（1996）  を図書館で借りて読んでみて下さい（買うと高い です）。ただし内容はかなり難しいです（著者も理 解できていないところが多々あります）。  また，後で述べるThomas-Fermi方程式の導出につ いても，かなり端折ります。
Thomas-Fermi-Diracのエネルギー汎関 数  LDAの下で，多電子系に対するエネルギー汎関数 ETFD[ρ]を書くと以下のようになる。  ただし，  これはThomas-Fermi-Diracのエネルギー汎関数と呼ば れる。そのためTFDというラベルを付けている。 運動エネルギー （電子－核間の） Coulombエネル ギー 電子-電子間の Coulombエネルギー （Hartreeエネルギー） 交換エネルギー
交換相互作用  交換（exchange）相互作用は電子のような同種 Fermi粒子の間で働く相互作用の一つである。  古典力学による交換相互作用の説明はできない。 典型的な量子力学の効果として説明される。  交換相互作用によるエネルギーを，交換エネル ギーといい，交換相互作用によるポテンシャルを 交換ポテンシャルという。
Thomas-Fermiエネルギー汎関数  第一近似として，交換エネルギー項を無視するな ら，  となる。これはThomas-Fermiエネルギー汎関数と 呼ばれる。そのためTFというラベルを付けている。 運動エネルギー （電子－核間の） Coulombエネル ギー 電子-電子間の Coulombエネルギー （Hartreeエネルギー） 交換エネルギー
Thomas-Fermi方程式を導く  実際に，原子に対するETF[ρ]を考えてみよう。原子 では， である（ここでZは原子番号）。  ここで，ETF[ρ]をρで汎関数微分すると，対応する Euler-Lagrange方程式が得られ，  である。ここで，μTFは化学ポテンシャル，φ(r)は古 典的なCoulombポテンシャルであり，  である。
Thomas-Fermi方程式を導く  中性原子を考えると，μTF = 0とならなければなら ない。従って，  である。これから，  である。ここで，古典的な電磁気学のPoisson方程 式をこの原子に適用すると，  である。
Thomas-Fermi方程式を導く  上記の二つの式を連立させ，変数変換を施すこと によって，最終的に  を得る。この非線形常微分方程式はThomas-Fermi 方程式と呼ばれる。ここで，  である（原子は球対称であることを用いた）。
Thomas-Fermi方程式を解く  上記のThomas-Fermi方程式は，非線形常微分方 程式であり，解析的には解けない。  従って，何らかの方法によって数値的に解く必要 がある。  著者は有限要素法（Finite Element Method, FEM） によって，数値的に解いた。  詳細は，Thomas-Fermi方程式のFEMによる解法 （ http://www.slideshare.net/dc1394/no-1- 27060987 ）を参照のこと。
Thomas-Fermiモデルの問題  残念ながら，Thomas-Fermi方程式の解から与えられる 結果（以下T-Fモデルと呼ぶ）は正しくない。  T-Fモデルの中性原子のエネルギーはおおむね- 0.7687Z7/3 (Hartree)となる（ここでZは原子番号であ る）。  ここで水素原子について考えれば，Schrödinger方程 式を解析的に解くことによって得られる，厳密な基底 状態のエネルギーは-0.5 (Hartree)であるが，T-Fモデ ルは54％も過大な値を与える。  その他の原子についても同様であり，ヘリウム原子で は35％，クリプトン原子では20％，そしてラドン原子 では15％過大な値を与える。
T-Fモデルの問題  T-Fモデルは，エネルギーのみならず，（電子）密度そのも のにおいても，物理的に誤った結果を与える。 水素原子におけるThomas- Fermi密度と厳密な密度 水素原子におけるThomas- Fermi密度と厳密な密度（y軸 対数目盛）密度が原点 で発散 密度が指数 関数で減衰 しない
T-Fモデルの問題  厳密な密度は，遠方で指数関数で減衰するが，T- Fモデルの密度は，遠方で距離rの6乗に反比例し て減衰する。  また，動径方向の電荷分布を示すr2ρ(r)も，原子 の正確な振る舞いを再現していない。 水素原子における動径方向のT-Fモデルでの電荷分布と厳密な電荷分布
T-Fモデルの問題  水素原子について，T-Fモデルにおける電荷分布 と，厳密な電荷分布を三次元プロットで示した。  T-Fモデルは，厳密な電荷分布を再現していない。 T-Fモデルの電荷分布 厳密な電荷分布
Thomas-Fermi-Diracモデル  Thomas-Fermi-Diracモデルでも，これは改善されな いばかりか，もっと悪くなる。  交換エネルギーは正であるので，与えられた電子 密度に対して，ETFD[ρ]はETF[ρ]よりもさらに，負の方 向に大きくなる。 運動エネルギー （電子－核間の） Coulombエネル ギー 電子-電子間の Coulombエネルギー （Hartreeエネルギー） 交換エネルギー
Thomas-Fermiモデルの改良と限界  Thomas-Fermiモデルの欠点を解決するため，改良さ れたモデルがいくつか提唱されている。  修正Thomas-Fermiモデル：Thomas-Fermiモデルの電子 密度は原点で不連続であるが，これを原点で連続に なるように改良する。  Thomas-Fermi-Dirac-Weizsackerモデル：Thomas-Fermi(- Dirac)モデルでは，原子（や分子）の電子密度の非一 様性を考慮していなかったため，精度が悪かった。そ こで，Thomas-Fermi運動エネルギーに対して，密度勾 配補正（Weizsacker補正）を加えて改良する。  …が，いずれも根本的な解決にはなっていない。
高次の密度勾配補正の限界  Thomas-Fermi運動エネルギーに対する，密度勾配補 正は，1粒子のGreen関数のWigner変換を半古典的 にℏ展開することで得られる（Weizsacker補正は2次の 密度勾配補正である）。  一見すると，高次の密度勾配補正を行えば，より高い 精度が得られるように思えるが，原子や分子の場合 には，これが正しいのは4次までである（6次の密度勾 配補正は発散してしまう）。  従って，この処方で精度を上げることは，見たところほ とんど不可能であり，代わりに現在では，次ページ以 降で述べるKohn-Sham法が使われている。
Kohn-Sham法  これまでのモデルのそもそもの問題点は，運動エ ネルギー汎関数T[ρ]の近似が粗すぎることにあっ た。  そこで，KohnとShamは1965年に，T[ρ]に対する， 巧妙な間接的アプローチを提案した。  この方法をKohn-Sham法と呼び，この方法によっ て，密度汎関数理論は，厳密な計算を行うための 実際的な道具となった。
Kohn-Shamの補助系  KohnとShamは，相互作用のある現実の系を，仮想 的な，「それと同じ密度を与える，相互作用のない 系の問題に置き換えて考える」ことを提案した。  これをKohn-Shamの補助系（Kohn-Sham auxiliary system）という。  この仮想的な系は，相互作用のない粒子からでき ているが，この系の基底状態の電子密度は，現実 の系の基底状態の電子密度と，全く同じである。  言い換えれば，この仮想的な系は，同じ密度（と 全エネルギー）を与える別の系である。
Kohn-Sham法の疑問  相互作用のある電子系の基底状態の密度はどの ようなものでも，相互作用のない電子系の基底状 態の密度として厳密に再現できるのだろうか？？  これは「相互作用のないv表示可能性」と呼ばれる。  この疑問に対する一般的な証明はない。  にもかかわらず，計算結果は非常に「理にかなっ て」いるように見えるので，Kohn-Sham法は正しい とされている（あるいは少なくともそう仮定されて いる）。  個人的には，なぜ「理にかなった」計算結果が得られるのか，非常に不 思議です。一般的な証明の論文が出たら，ぜひ読んでみたいです。
Kohn-Sham方程式  KohnとShamは，以上のような定式化に基づき，以 下の方程式を導いた。  これは，Kohn-Sham方程式と呼ばれる（簡単のた めスピン次元は省略した）。ここで，veff(r)は，  である。 （核による）外部 ポテンシャル 電子による古典的なCoulomb ポテンシャル（Hartreeポテン シャル） 運動エネルギーポテンシャル KS有効ポテンシャル KS有効ポテンシャル 交換相関ポテン シャル （エネルギー）固有値
相互作用のない系の意味  Kohn-Shamの補助系において，「相互作用のない系」 とは，電子－電子間の相互作用を全て無視する，と いう意味ではない。  例えば，他の電子から受ける古典的なCoulomb相互 作用は，Kohn-Sham方程式において，Hartreeポテン シャルとして取り入れられている。これは，電子の平 均的な電荷分布から生じる静電ポテンシャルである。  ところで，Kohn-Sham方程式には，直接的な電子－電 子間の相互作用の項が含まれていない。  結果として，Kohn-Sham方程式は一粒子に対する Schrödinger方程式の形をしている（一粒子近似）。こ れを「相互作用のない」と呼んでいる。
Kohn-Sham方程式の解法  Kohn-Sham方程式は，以下のような非線形連立偏 微分方程式であり，反復計算法によって解かなく てはならない。これを自己無撞着場の方法（Self- Consistent Field Method, SCF法）という。 この反復を，入力 と出力が一致する まで行う （＝SCFの達成）。 このとき，全電子 エネルギーEKS[ρ] は最小値をとる。
Kohn-Sham方程式の固有値と固有関 数の物理的意味  Kohn-Sham方程式の（エネルギー）固有値は，相互作 用していない仮想的な系の固有値であるので，直接 には（たった一つの例外を除き）どんな物理的な意味 も持っていない。  従って，Kohn-Sham方程式の固有値を実際の系のも のと見なすことはできない。  しかし，それはしばしば実験値と比較される。  なお，「たった一つの例外」とは有限の系の最も高い 固有値であり，これは系のイオン化エネルギーの符 号を変えたものと等しい。  また，固有関数（波動関数）においても，同じことが言 える（こちらは例外なく）。
Kohn-Sham法の全エネルギー  密度ρ(r)が求まったならば，N電子系のKohn-Sham 法の全電子エネルギーEKS[ρ]は以下の式で求めら れる。  すでに述べたとおり，SCFが達成されたとき， EKS[ρ]は（大局的な）最小値をとる。  全電子エネルギーは，各軌道の固有値の総和と ならないことに注意。 電子-電子間のCoulombエ ネルギー （Hartreeエネルギー） 各軌道の固有値の総 和 交換相関エネルギー おつりの項
Janakの定理  「Kohn-Sham方程式の固有値を実際の系のものと 見なすことはできない」が，それはまた「実験値と 比較される」と述べた。  これは，Kohn-Sham法において成り立つ，以下の Janakの定理により，ある程度正当化される。  ここでniは，軌道を電子が占有し，非整数による占 有が可能とした場合の軌道の占有数である。
Janakの定理  イオン化エネルギーを，i番目の軌道から，電子を 1個取り去るためのエネルギーだと定義する。  ここで，Hartree-Fock法におけるKoopmansの定理 によれば， であり，この-εiは，イオン 化エネルギーと等しい。  ここで，ENはN個の電子からなる系の基底状態に おける全エネルギーであり， EN-1は，その系から 電子を1個取り出した場合，つまりN-1個の電子か らなる系の全エネルギーである。  ただし，電子を取り去ることに対し，一電子波動関 数は不変であると仮定している。
Janakの定理  ここで，上式の左辺は差分ではなく微分になって おり，このため，エネルギー固有値εiはイオン化エ ネルギー（の符号を変えたもの）であるとは言えな い。  しかし同時に，差分と微分の差が小さいと仮定す れば， Kohn-Sham法においても，エネルギー固有 値を，イオン化エネルギーと見立てても良いとい うことになる。  こうして， 「実験値と比較する」ことが，ある程度正 当化される。
交換相関ポテンシャル  すでに紹介したように，同種Fermi粒子の間で働く相 互作用の一つである，交換相互作用によるポテン シャルを交換ポテンシャルという。  また，運動エネルギー，Coulomb相互作用，そして交 換相互作用以外の全ての相互作用を相関相互作用 といい、相関相互作用によるポテンシャルを相関ポテ ンシャルという。  交換ポテンシャルと相関ポテンシャルを合わせて，交 換相関ポテンシャルと書くことも多い。  Kohn-Sham法において，相関ポテンシャルには，「相 互作用のある」実際の系の運動エネルギーによるポ テンシャルと，「相互作用のない」仮想的な系の運動 エネルギーによるポテンシャルの差も含まれる。
相関相互作用について  相関相互作用によるエネルギー（相関エネルギー）は， 系にもよるが，概ね全エネルギーの1％程度に過ぎな い。  しかし，この相関相互作用を無視することは，しばし ば非物理的な結果をもたらす。  そして， 相関相互作用が重要である「強相関電子系」 と呼ばれる系（高温超伝導体がその一例）は，現在の 標準的な密度汎関数理論では，正確に物性を記述で きない（DFT+Uと呼ばれる方法もあるが，根本的な解 決にはなっていない）。  相関相互作用は，多体問題の理論における主要な問 題の一つであり，多大な研究努力が今なお続けられ ている。
交換相関汎関数  厳密な交換相関汎関数を探す試みは，未だに密 度汎関数理論における最大の挑戦課題である。  すでに紹介した局所密度近似（LDA）は最も簡単 な近似である。これに電子のスピンを考慮したも のを局所スピン密度近似（Local Spin Density Approximation, LSDA）という。  さらに，L(S)DAを密度の勾配∇ρ(r)を用いて補正し たものを一般化勾配近似（Generalized Gradient Approximation, GGA）という。
交換相関汎関数  この他，GGAを二次密度勾配∇2ρ(r)と運動エネ ルギー密度τ(r)を使って補正したmeta-GGAや， hybrid-GGAなどがある。  さらに，L(S)DA, GGAなどとひとくくりにされるグ ループの中にも，様々な表式が存在する。  従って，交換相関汎関数には様々なバリエーショ ンが生まれる。  これは，交換相関汎関数の厳密な表式（おそらく 非常に複雑なもの）を得るのがいかに難しいかを， 暗に示しているように思われる。
例：Kohn-Sham法で計算した水素原子 の電子密度  水素原子に対して，Kohn-Sham方程式を解き，得られた電 子密度を厳密な電子密度と比較した。なお，交換相関汎 関数にはGGA-PBEを用いた。  T-Fモデルの電子密度よりも，はるかに厳密な電子密度と 近いことが分かる。 水素原子におけるKohn- Sham密度と厳密な密度 水素原子におけるKohn- Sham密度と厳密な密度（y軸 対数目盛）
例：Kohn-Sham法で計算した水素原子 のエネルギーと電荷分布  GGA-PBE交換相関汎関数を用いた場合，Kohn- Sham方程式を解いて得られる水素原子の基底状 態のエネルギーは，-0.49999 (Hartree)であり，こ れは厳密な値の99.998％である。  また，動径方向の電荷分布を示すr2ρ(r)は，原子 の正確な振る舞いをほぼ再現している。 水素原子における動径方向のKohn-Sham法での電荷分布と厳密な電荷分布
例：Kohn-Sham法で計算した水素原子 の電荷分布  水素原子について，Kohn-Sham方程式を解いて得 られる電荷分布と，厳密な電荷分布を三次元プ ロットで示した。  Kohn-Sham法は，厳密な電荷分布を再現している。 Kohn-Sham法による電荷分布 厳密な電荷分布
交換相関汎関数（参考サイト，文献）  このスライドでは，様々な交換相関汎関数について， これ以上説明することは止めておきます（何より著者 自身が，具体的な交換相関汎関数の物理的背景を 全くといっていいほど理解できていない）。  交換相関汎関数についてより詳しく知りたい方は，ま ずは理化学研究所の方が書かれたスライドを読んで みることをおすすめします （ http://www.riken.jp/qcl/members/tsuneda/web/dft0 5-sec2.pdf ）。  この方が書かれた本も非常に参考になります：常田 貴夫 『密度汎関数法の基礎』講談社（2012）  これも買うと高いので，興味のある方は図書館で借り て読んでみることをおすすめします。
第一原理計算における計算手法  ここまで，密度汎関数理論（とKohn-Sham法）の概 略を紹介してきた。  現在行われている第一原理計算では，たいてい Kohn-Sham方程式を基礎方程式として，これを解く ことで何らかの意味のある物理量を得ている。  第一原理計算で用いられる，それ以外の方法とし ては，例えば量子モンテカルロ（Quantum Monte Carlo, QMC）法が挙げられる。この方法は，電子 の多体問題をより直接的に扱うため，精度は高い が計算コストも高い。  また，GW近似といわれる方法も存在する。
第一原理計算におけるさらなる工夫  第一原理計算において，実際にKohn-Sham方程式 を解くには，さらなる工夫が必要である。  この工夫とは，例えば基底の導入（平面波基底， Gauss関数基底，数値基底，有限要素基底など） や，擬ポテンシャルの導入などである。  さらに，この他にも様々な手法，例えばFP-LAPW (Full-Potential Linearized Augmented Plane Wave) 法，FP-LMTO (Full-Potential Linear Muffin-Tin Orbital)法，KKR (Korringa-Kohn-Rostoker)法などが ある。
第一原理計算ソフトウェア一覧  このような手法の違いにより，第一原理計算ソフト ウェアも，様々なものが存在している。  具体的なソフトウェア名は，例えばWikipediaの項 目（ http://bit.ly/16bblUu ）や，CMSI webの記述 （ http://bit.ly/16bbnvr ），あるいはPsi-k （ http://bit.ly/16bbszl ）を参照のこと。  この他にも，研究室で開発されているが，外部に 非公開のソフトウェアが多数あるのは間違いない。  実際，著者が某研究室に在籍していたとき，その 研究室のソフトウェアは内部のみの公開であった。
第一原理計算で得られる情報  固有関数（Kohn-Sham法では，厳密には波動関数と見 なせない）  バンド分散，状態密度，Fermi面，バンドギャップ  平衡格子定数，体積弾性率  電荷解析（Mulliken電荷，Voronoi電荷， ESPフィッティ ング等）  分極（これは難しい問題，「Berry位相」の第一原理シ ミュレーションもされている）  電気伝導特性，磁性  フォノン分散  …など，他にも多数
第一原理計算を試してみたい方へ  本格的に第一原理計算をするなら，自作するより既存のソフト ウェアを使った方がよい。  しかし，「第一原理計算を行う」ことと，「第一原理計算を理解す る」ことは別である。  一般に，たとえGPLライセンス等のオープンソースなソフトウェア であっても，ソースコードの全てに目を通し，また理解するのは困 難。  しかし，「第一原理計算を理解する」ためには，これは必要なス テップである（少なくとも、ソースコードの内容を理解する努力は 必要である）。  結局，既存のソフトウェアを使用することは，「入力ファイルを編集 して，バイナリを実行するだけ」となってしまう。  個人的には，第一原理計算（とそのコードの構造）を理解するには，既存のコードを参 考にしつつ，自分でコードを書いてみるのが一番手っ取り早いかなと思っています。
第一原理計算を試してみたい方へ  最近では，小規模な分子・固体といった系なら， PC上で計算できるようになった。  しかし，大規模な分子・固体といった巨大な系の 計算には，未だに大量のCPUコアとメモリを必要と する。  従って、そのような系の計算は，スーパーコン ピュータ（HPC）上で行われる。  しかし，それでも長い計算時間が必要（自分の経 験から言えば，少なくとも数日から一週間）。
参考文献  R.G.パール, W.ヤング 『原子･分子の密度汎関数 法』シュプリンガー・フェアラーク東京（1996）  R.M.マーチン 『物質の電子状態 上』シュプリン ガー・ジャパン株式会社（2010）  R.M.マーチン 『物質の電子状態 下』シュプリン ガー・ジャパン株式会社（2012）  J.M.ティッセン 『計算物理学』シュプリンガー・フェ アラーク東京（2003）
参考サイト  1.5 密度汎関数法 - 講義資料: http://www.riken.jp/qcl/members/tsuneda/web/p ages/siryo/qchem3-5.pdf  「密度汎関数法とは」（分子研・2005年12月）: http://www.riken.jp/qcl/members/tsuneda/web/df t05.html  第一原理計算と密度汎関数理論: http://www.cmp.sanken.osaka- u.ac.jp/~koun/Lecs/dft.pdf  第一原理バンド計算 - Wikipedia: http://bit.ly/16b9EpT
参考サイト  第一原理計算入門: http://www5.hp- ez.com/hp/calculations/page1  ５月１１日：密度汎関数理論 波動関数的世界観か ら密度的世界観へ - 物性物理学IA 平成19年度 前期東京大学大学院講義: http://takada.issp.u- tokyo.ac.jp/CMPIA-05-07.pdf  バンド計算関連用語集 – Important glossary for electronic structure calculations: http://www.geocities.co.jp/technopolis/4765/INTR O/yogo.html
参考サイト  A LDA+U study of selected iron compounds – SISSA: http://www.sissa.it/cm/thesis/2002/cococcioni.pdf  上記はLDA+U（DFT+Uの一種）についての論文（英 語）ですが，第一原理計算（そして平面波基底と 擬ポテンシャル）について，一通りのことがまと まっていて，非常に良い論文です。
参考サイト  「おまけ」で，前ページで紹介した論文を，著者が 和訳したもののURLを載せておきます（ただし第二 章の途中まで。間違っている場所が多数あると思 うので，あくまで「参考」に）。  第一章: http://www.slideshare.net/dc1394/a- ldau-study-of-selected-iron-compounds  第二章: http://www.slideshare.net/dc1394/a- ldau-study-of-selected-iron-compounds-26424474

More Related Content

第一原理計算と密度汎関数理論