Stacks.ppt

Templates in C++
 Template function in C++ makes it
easier to reuse classes and functions.
 A template may be viewed as a variable
that can be instantiated to any data
type, irrespective of whether this data
type is a fundamental C++ type or a
user-defined type.

Two min() Functions
int min(int a, int b) {
return a < b ? a : b;
}
double min(double a, double b) {
}
The following program shows the weakness of
strongly-typed languages:

The Template Solution
template <class Type>
Type min(Type a, Type b) {
}
main() {
// ok: int min(int, int);
min(10, 20);
// ok: double min(double, double);
min(10.0, 20.0);
}

What is a stack?
 It is an ordered group of homogeneous items of elements.
 Elements are added to and removed from the top of the stack
(the most recently added items are at the top of the stack).
 The last element to be added is the first to be removed (LIFO:
Last In, First Out).

The Stack ADT
 A stack is a list with the restriction
 that insertions and deletions can only be performed at the
top of the list
 The other end is called bottom
 Fundamental/Primitive operations:
 Push: Equivalent to an insert
 Pop: Deletes the most recently inserted element
 Empty: Examines whether the stack is empty

Stack ADT
 Stacks are less flexible
 but are more efficient and easy to
implement
 Stacks are known as LIFO (Last In, First
Out) lists.
 The last element inserted will be the first to
be retrieved

EXAMPLE
Push 5, 3, 1, Pop, Pop, Push 7
Push 5
Push 3 Push 1
Pop Pop Push 7
5 5
3 3
5
1
5
3
Get 1
5 5
7
Get 3

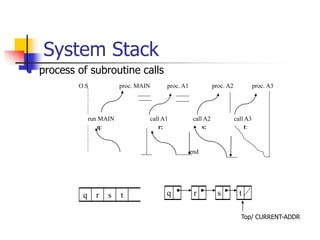
System Stack
 process of subroutine calls
q r s t q r s t
Top/ CURRENT-ADDR
O.S proc. MAIN proc. A1 proc. A2 proc. A3
run MAIN call A1 call A2 call A3
q: r: s: t:
end

Function Calls
When a subroutine calls another subroutine
(including itself) it must first store its register
contents.
So, it pushes the register contents into a stack.
The new function uses the registers.
When the program returns to the old function, pop
the stack.
Nested Function and Stack Overflow

ADT 3.1 Abstract Data Type
Stack
template <class KeyType>
class Stack
{ // objects: A finite ordered list with zero or more elements
public:
Stack (int MaxStackSize = DefaultSize);
~Stack();
// Create an empty stack whose maximum size is MaxStackSize
bool IsFull();
// if number of elements in the stack is equal to the maximum size
// of the stack, return TRUE(1) else return FALSE(0)
bool IsEmpty();
// if number of elements in the stack is 0, return TRUE(1) else return FALSE(0)

ADT 3.1 Abstract Data Type
Stack (cont.)
KeyType Top();
// Return top element of stack
void Push(const KeyType& item);
// if IsFull(), then StackFull(); else insert item into the top of the stack.
KeyType Pop( );
// if IsEmpty(), then StackEmpty() and return 0;
// else remove the top element of the stack.
};

Implementation of Stack by
Array
 Implementation of stack ADT
 use an one-dim array stack[MaxSize]
 bottom element is stored in stack[0]
 top points to the top element
 initially, top=-1 for an empty stack
 data member declarations in class
template < class KeyType >
class Stack
private:
int top;
KeyType *stack;
int MaxSize;
public:
......
a0
a1
a2
Array index
0 1 2 3 n-1
a0 a1 a2
an-1
an-1

Array (cont.)
 constructor definition
 member function IsFull()
Stack<KeyType>::Stack (int MaxStackSize) : MaxSize (MaxStackSize)
{
stack = new KeyType[MaxSize];
top = -1;
}
inline bool Stack<KeyType>::IsFull()
{
if (top == MaxSize-1) return TRUE;
else return FALSE;
}

Array (cont.)
 member function IsEmpty()
 member function Top()
inline bool Stack<KeyType>::IsEmpty() { return top == -1;}
inline KeyType& Stack<KeyType>::Top()
{
if (IsEmpty()) throw “Stack is empty”;
return stack[top];
}

Array (cont.)
 Push operation
 Pop operation
KeyType Stack<KeyType>::Pop()
{ // Remove top element from stack.
if (IsEmpty())
{cout << “Stack Overflow”; exit(-1);}
return stack[top--];
}
void Stack<KeyType>::Push(const KeyType& x)
{ // add x to stack
if (IsFull()) {cout << “Stack Overflow”; exit(-1);}
else stack[++top] = x;
}

Example
Consider a mathematical expression that includes several sets of nested
parenthesis.
7 – ((x * (( x + y) / (j - 3)) + Y) / (4 – 2))
In expression we want to check
1.There are an equal number of right and left parenthesis.
2. Every right parenthesis is preceded by a matching left parenthesis.
Expressions like ((A+B) or A+B( violates condition 1 and expressions like )A
+ B(-C violate condition 2.
Nested Depth: is the number of scopes that have been opened and not
yet closed.
Parenthesis count: no of left parenthesis – no of right parenthesis.

Example (Cont’d)
Expression id valid if following conditions are met.
1. Parenthesis count at end should be zero.
2. Parenthesis count at each point in expression should be non negative.
7 – ( ( x * ( ( x + y ) / ( j - 3 ) ) + Y ) / ( 4 – 2.5 ) )
0 0 1 2 2 2 3 4 4 4 4 3 3 4 4 4 4 3 2 2 2 1 1 2 2 2 2 1 0
( ( A + B ) and (A + B] is illegal
1 2 2 2 2 1

Algorithm for Example
valid = true
s = empty stack;
while (we have not read the entire string) {
read the next symbol (symb) in the string;
if (symb == ‘(’ || symb == ‘{’ || symb == ‘[’ )
s.push(symb);
if (symb == ‘)’ || symb == ‘}’ || symb == ‘]’ )
if (empty(s))
valid = false;
else{
i = s.pop();
if (i is not the matching opener of symb)
valid = false }
}// end of while
if (!s.empty()) valid = false;
if (valid)
cout << “String is valid”;
else cout << “String is not valid”;

Parenthesis Stack
Consider expression
[x + {y – (a + b)}]
[ [
{
[
{
[
{
(
[ [ x+{ [ x+{y-( [ x+{y-(a+b)
[
[ x+{y-(a+b)} [ x+{y-(a+b)}]

Polish Notations
Expression can be written in prefix, postfix or infix
notations
 + A B prefix operator precedes operands
 A B + postfix operator precedes operands
 A + B infix
 Unlike Infix notation no parenthesis are
required to enforce precedence.
 Expressions are evaluated from left to
right.

Converting to Prefix, Postfix Notation
Precedence rules are used to convert expression
1) Exponentiation, 2. Multiplication/ Division 3. Addition/Subtraction
Converting to Prefix Notation
 (A+B)*C = [+AB]*C = *+ABC
 A+(B*C) = A+[*BC) = +A*BC
 (A+B)/(C-D)= [+AB]/[-CD] = /+AB-CD
Converting to Postfix Notation
 Ex. A+B= AB+
 (A+B)*C= [AB+]*C= AB+C*
 A+(B*C) = A+[BC*]=ABC*+

Exercises
 A$B*C-D+E/F/(G+H)
 ((A+B)*C-(D-E))$(F+G)
 A-B/(C*D$E)
 (A+B$D)/(E-F)+G
 A*(B+D)/E-f*(G+H/K)

Example: postfix expressions
(cont.)

Postfix expressions: using
stacks (cont.)

Postfix expressions: Algorithm
using stacks (cont.)
opndstk = the empty stack;
while (not end of input){
symb = next input character;
if (symb is an operand)
opndstk.push(symb);
else{
opnd2 = opndstk.pop();
opnd1 = opndstk.pop();
value = result of applying symb to opnd1 and opnd2;
opndstk.push(value) }

EXERCISE
6 2 3 + - 3 8 2 / + * 2 $ 3 +
symb op1 op2 value opndstk
6
2
3
+
-
3
8
2
/
+
*
2
$
3
+
2
6
6
6
6
8
3
1
1
7
7
49
3
5
5
5
5
2
4
7
7
2
2
3
5
1
1
1
1
4
7
7
7
49
49
52
6
6 2
6 2 3
6 5
1
1 3
1 3 8
1 3 8 2
1 3 4
1 7
7
7 2
49
49 3
52

Algorithm to Convert Infix Exp
to Postfix Expression
1. opstk = the empty stack;
2. while (not end of input){
3. symb = next input character;
4. if (symb is an operand)
add symb to the postfix string
5. else{
6. while (!opstk.empty () && prcd(opstk.Top(), symb)){
7. topsymb = opstk.pop();
8. add topsymb to the postfix string;
} /* end while*/
9. opstk.push(symb);
} /* end else*/
} /* end while*/
10. while (!opstk.empty()){
11. Topsymb = opstk.pop();
12. add topsymb to the postfix string;
} /* end while*/

EXERCISE
A + B * C
symb Postfix string opstk
A
+
B
*
C
A
A
AB
AB
ABC
ABC*+
+
+
+ *
+*

EXERCISE
A * B + C
symb Postfix string opstk
A
*
B
+
C
A
A
AB
AB*
AB*C
AB*C+
*
*
+
+

Algorithm to Convert Infix Exp
to Postfix Expression
9. if (opstk.empty () || symb != ‘)’)
opstk .push(symb);
else
topsymb = opstk.pop();
Precedence rules for parenthesis:
prcd(‘(’,op) = FALSE
Prcd(op,’(’) = FALSE
prcd(op,’)’) = TRUE
prcd(‘)’,op) = undefined

Evaluation of Expressions
 Consider the following infix expression
 A+(B*C-(D/E$F)*G)*H
 Convert into Postfix using Stack
sumb postfix string opstk
A
+
(
B
*
C
-
(
D
/
E
$
F
)
*
G
)
*
H
+
+ (
+ (
+ ( *
+ ( *
+ ( -
+ (- (
+ ( - (
+ ( - ( /
+ ( - ( /
+ (- ( /$
+ ( - ( / $
+ ( -
+ ( - *
+ ( - *
+
+ *
+ *
A
A
A
A B
A B
A B C
A B C *
A B C *
A B C * D
A B C * D
A B C * D E
A B C * D E
A B C * D E F
A B C * D E F $ /
A B C * D E F $ / G
A B C * D E F $ / G * -
A B C * D E F $ / G * -
A B C * D E F $ / G * - H
A B C * D E F $ / G * - H * +

Converting Infix Expressions to Equivalent
Postfix Expressions
Figure 6.9
A trace of the algorithm that converts the infix expression a - (b + c * d)/e to postfix form

Stacks.ppt

More Related Content

Stacks.ppt