Thermal analysis of cooling effect on gas turbine blade

IJRET: International Journal of Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308
__________________________________________________________________________________________
Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 603
THERMAL ANALYSIS OF COOLING EFFECT ON GAS TURBINE
BLADE
Amjed Ahmed Jasim AL-Luhaibi1
, Mohammad Tariq2
1
Technical collage Kirkuk, Fuel and Energy Engineering Department, Foundation of Technical Education, Iraq
2
Assistant Professor, Department of Mechanical Engineering, SSET, SHIATS-DU, Allahabad
Abstract
Performance of a gas turbine is mainly depends on various parameters e.g. ambient temperature, compressor pressure ratio, turbine
inlet temperature etc. The most important parameter to increase the life of the turbine blade is the cooling of the blade, which is
necessary after reaching a certain temperature of the gases passing through the blades. Various types of cooling models are available
for a turbine blade cooling. The power output of a gas turbine depends on the mass flow rate through it. This is precisely the reason
why on hot days, when air is less dense, power output falls off. This paper is to analyze the film cooling technique that was developed
to cool gases in the initial stages of the turbine blades, where temperature is very high (>1122 K). It is found that the thermal
efficiency of a cooled gas turbine is less as compare to the uncooled gas turbine for the same input conditions. The reason is that the
temperature at the inlet of the turbine is decreased due to cooling and the work produced by the turbine is slightly decreased. It is also
found that the power consumption of the cool inlet air is of considerable concern since it decreases the net power output of gas
turbine. In addition, net power decreases on increasing the overall pressure ratio. Furthermore, the reviewed works revealed that the
efficiency of the cooled gas turbine largely depends on the inlet temperature of the turbine and previous research said that the
temperature above 1123K, require cooling of the blade.
Keywords: Gas turbine, Turbine blade cooling, film cooling technique, Thermal Efficiency
----------------------------------------------------------------------***--------------------------------------------------------------------
1. INTRODUCTION
In a bid to remain at the forefront of technological
development as well as a technical expert to United States
industry, NASA identified the need for an improved design
process within the civilian aero engine industry, in hopes of
improving their market share, reducing time to market, and
minimizing research costs [2]. Areas of interest included, but
were not limited to, high temperature materials, advancing
turbine analysis techniques, and improving the overall engine
design and analysis process. The latter interest called for the
impact assessment of engine component technologies from the
micro to system levels [2]. A good example of the need for
this type of analysis comes from determining the required
service life of a turbine blade, which is limited by the exit
temperature from the combustor and the material properties
that in turn, limits the performance of the gas turbine. Ideally,
the engine would operate at a high enough temperature to
achieve the highest possible thrust rating [3], while at the same
time maintaining an economic service life. Currently, to
address the issue of exit temperature, modern turbines utilize a
cooled turbine blade to improve the possible rotor inlet
temperature, and this necessary cooling flow has a strong
impact on the turbine efficiency [4, 5]. By improving cooling
technology for a gas turbine blade it is possible to increase the
combustor exit temperature sufficiently, therefore achieving
good improvement in turbine efficiency and thrust [6].
However, this improvement does not prove viable when
considering the complete process. The increase in cooling
flow to the turbine blades and vanes takes bleed air away from
the compressor, reducing its on efficiency. This detrimentally
affects the efficiency of the whole system, such that the
improvements in the turbine are eclipsed. Being able to track
all these whilst looking at a particular component within an
aircraft gas turbine, is obviously very desirable, especially at
the early stages of a design. A successful design process
incorporates flexibility and freedom at the early conceptual
stages and continuing as far into the design as possible, saving
time and money in fixing problems that would have arisen had
an investigation not taken place. Looking into technologies to
improve an engine, one needs to provide useful benchmarks
from which comparisons can be made. If a superior product is
going to be produced, analysis of the areas affected by the new
product needs to be considered. If this is not the case a lot of
money could be invested in designs that in the end prove to be
impractical. A new technique has been reviewed up to date
that was developed to cool inlet air to gas turbine [9]. The
techniques including the mechanical chillers, media type
evaporative coolers and absorption chillers have been
reviewed. It is found that the power consumption of the cool
inlet air is of considerable concern since it decreases the net
power output of gas turbine. Experimental tests to investigate
the film cooling performance of converging slot hole (console)
rows on the turbine blade have been performed [10]. Film
cooling effectiveness of each single hole row is measured

__________________________________________________________________________________________
under three momentum flux ratios based on the wide-band
liquid crystal technique. Measurements of the cooling
effectiveness with all the hole rows open are also carried out
under two coolant–mainstream flux ratios. Film cooling
effectiveness of cylindrical hole rows on the same blade model
is measured as a comparison. The thermodynamic
performance of MS9001 gas turbine based cogeneration cycle
having a two-pressure heat recovery steam generator (HRSG)
for different blade cooling means have compared. Internal
convection cooling technique, film cooling and transpiration
cooling techniques, employing steam or air as coolants, are
considered for the performance evaluation of the cycle[11].
The analysis is useful for power plant designers to select the
optimum compressor pressure ratio, turbine inlet temperature,
fuel utilization efficiency, power-to-heat ratio, and appropriate
cooling means for a specified value of plant specific work and
process heating requirement. The gas turbine plant
performance and the effects of turbine cooling have been
presented [8]. The thermal efficiencies are determined
theoretically, assuming air standard (a/s) cycles, and the
reductions in efficiency due to cooling are established; it is
shown that these are small, unless large cooling flows are
required. The theoretical estimates of efficiency reduction are
compared with calculations, assuming that real gases form the
working fluid in the gas turbine cycles.
2. METHODOLOGY
2.1 Open Gas Turbine Cycle
Fig. 1: Schematic for an open gas-turbine cycle
Fresh air enters the compressor at ambient temperature where
its pressure and temperature are increased. The high pressure
air enters the combustion chamber where the fuel is burned at
constant pressure. The high temperature (and pressure) gas
enters the turbine where it expands to ambient pressure and
produces work.
Fig 2 T-s representation of a gas turbine engine
2.2 Gas Model
The thermodynamic properties of air and products of
combustion are calculated by considering variation of specific
heat and with no dissociation. Table containing the values of
the specific heats against temperature variation have been
published in many references. Following equations are used to
calculate the specific heats of air and gas as a function of
temperatures.
For Ta ≤ 800 the value of cpa will be calculated from the
following equation.
cpa = 1.0189 × 103
− 0.13784 × Ta + 1.9843 ×
10−4×Ta2+4.2399×10−7×Ta3−3.7632×10−10×Ta4 (1)
In the above equations, T stands for gas or air temperature in
deg K and t =
T
100
Compressors are subjected to various aerodynamic losses
which are accounted here by introducing the concept of
polytropic efficiency. For a given polytropic efficiency,
pressure ratio and bleed point pressure, the temperature and
other variables for each stream are calculated. The mass and
energy balances yield the compressor work, as given below
Mass balance:
ma,i = ma,e + mcl (2)

__________________________________________________________________________________________
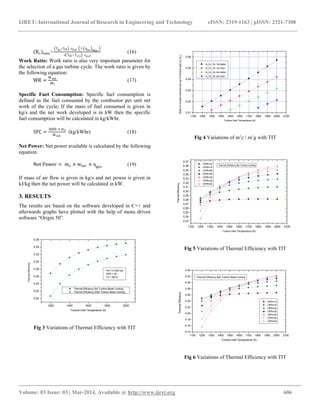
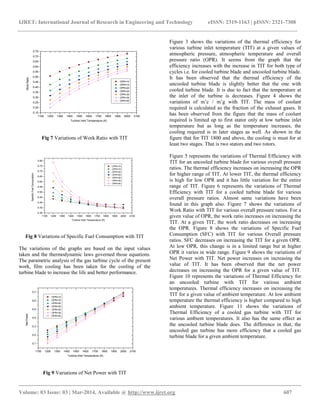
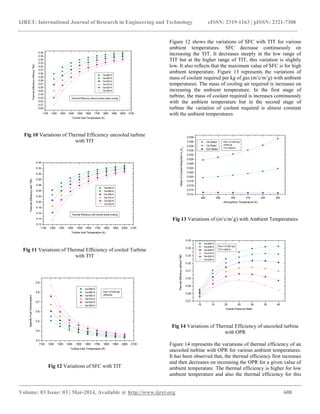
Energy balance:
Wc = ma,e . ha,e + mcl . hcl − ma,i. ha,i (3)
Where determination of mcl (mass of the cooling air) extracted
from the compressor, is given after turbine cooling flow
calculation.
p2 = p1
p2
p1
(4)
T2 − T1 =
T1
ηc
p2
p1
γ a −1
γ a
− 1 (5)
T2
T1
=
p2
p1
γa −1
ηpc .γ a
(6)
Where
p2
p1
is the overall pressure ratio of compressor and ηc
and ηpc are isentropic and polytropic efficiencies of the
compressor, respectively.
2.3 Combustion Chamber
The purpose of the combustion system of a gas turbine engine
is to increase the thermal energy of a flowing gas stream by
combustion which is an exothermic chemical reaction between
the hydrocarbon fuel and oxygen in the air-stream. Inflowing
air is diffused at the entrance of the burner. Kerosene is the
standard aviation fuel but the highly distilled forms of diesel
used make little difference in performance compared to
kerosene and hence diesel is used here for the analysis. The
mass and energy balances for combustor, with suffixes i and e
denoting its inlet and outlet sections, are given by
Mass balance:
mg = ma,i + mf,cc (7)
Energy balance:
ηcc
. mf,cc . LCVf = mg,e. hg,e − ma,i. ha,i (8)
The pressure at combustor exit is given by (Δpcc =2%
pressure drop has been assumed in the combustor)
pcc,e = p cc,i − Δpcc (9)
The fuel to air ratio (FAR) is calculated as,
mf,cc
ma
=
cpg .Te −cpa .Ti
ηcc .LCV f −cpg .Te
(10)
In this equation Te is the turbine inlet temperature, Ti is exit
temperature of compressor, ηcc
is the combustion efficiency of
the main combustion chamber, normally taken between 0.98
to 0.99 and LCVf is the lower calorific value of the fuel taken
as 42000 kJ/kgK assuming fuel as diesel. Values of specific
heat of air and gases are to be calculated from the gas model.
2.4 Cooled Gas Turbine
Turbine produced power to drive engine compressor due to
expansion of gas stream apart from the excess work developed
at the shaft of the turbine. A general model that represents the
gas turbine with turbine blade cooling has been developed.
The model is intended for use in cycle analysis applications.
Aerodynamic losses and hence the inefficiency of gas turbine
is taken care by considering polytropic efficiency of turbine.
Ti
Te
=
pi
pe
ηpt . γt−1
γt
(11)
Pressure ratio, the temperature and other variables for each
stream are calculated for a given polytropic efficiency. Wt is
the work developed by turbine, and ηm
is the mechanical
efficiency which is used to account for the losses due to
windage, bearing friction, and seal drag and is defined as
ηm
=
mechanical power output
mechanical power input
Mass and energy balances yield the turbine work, as given
below.
Mass balance:
mg,i = mg,e + mcl (12)
Where
mg,i = ma,i + mf,cc (13)
and mcl represents the sum of air coolant flow rates to the
stage (stator and rotor).
Energy balance:
mg,i. hg,i + mcl,i. hcl,i = mg,e. hg,e+ WT (14)
Mass of coolant required per kg of gas flow is given by
following equations as explained in [8].
mcl
mg
=0.0156. Rc trans (15)
ηiso film
= 0.4
Where

__________________________________________________________________________________________
Rc trans=
Tg,i-Tbl . cp,g. 1- ηiso film
ε Tbl−Tcl,i . cp,cl
(16)
Work Ratio: Work ratio is also very important parameter for
the selection of a gas turbine cycle. The work ratio is given by
the following equation:
WR =
Wnet
Wt
(17)
Specific Fuel Consumption: Specific fuel consumption is
defined as the fuel consumed by the combustor per unit net
work of the cycle; If the mass of fuel consumed is given in
kg/s and the net work developed is in kW then the specific
fuel consumption will be calculated in kg/kWhr.
SFC =
3600 × mf
Wnet
(kg/kWhr) (18)
Net Power: Net power available is calculated by the following
equation.
Net Power = ma × wnet × ηgen
(19)
If mass of air flow is given in kg/s and net power is given in
kJ/kg then the net power will be calculated in kW.
3. RESULTS
The results are based on the software developed in C++ and
afterwards graphs have plotted with the help of menu driven
software “Origin 50”.
1200 1400 1600 1800 2000
0.20
0.22
0.24
0.26
0.28
0.30
0.32
0.34
0.36
Pa=1.01325 bar
OPR = 30
Ta = 300 K
Thermal Efficiency (No Turbine Blade Cooling)
Thermal Efficiency (With Turbine Blade Cooling)
ThermalEfficiency
Turbine Inlet Temperature (K)
Fig 3 Variations of Thermal Efficiency with TIT
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.01
0.02
0.03
0.04
0.05
0.06
mc
'
/m
'
g
for 1st stator
mc
'
/m
'
g
for 1st rotor
mc
'
/m
'
g
for 2st stator
mc
'
/m
'
g
for 2st rotor
MassofCoolantrequiredperkgofExhaustgas(mc
'
/m
'
g
)
Fig 4 Variations of m’c / m’g with TIT
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.23
0.24
0.25
0.26
0.27
0.28
0.29
0.30
0.31
0.32
0.33
0.34
0.35
0.36
0.37
Thermal Efficiency No Turbine Cooling
OPR=10
OPR=15
OPR=20
OPR=25
OPR=30
OPR=35
OPR=40
ThermalEfficiency
Turbine Inlet Temperarture (K)
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.14
0.16
0.18
0.20
0.22
0.24
0.26
0.28
0.30
0.32
0.34
Thermal Efficiency with Turbine Blade Cooling
OPR=10
OPR=15
OPR=20
OPR=25
OPR=30
OPR=35
OPR=40
ThermalEfficiency

__________________________________________________________________________________________
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
0.65
0.70
0.75
OPR=10
OPR=15
OPR=20
OPR=25
OPR=30
OPR=35
OPR=40
WorkRatio
Fig 7 Variations of Work Ratio with TIT
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.30
0.35
0.40
0.45
0.50
0.55
0.60
0.65
0.70
0.75
0.80
OPR=10
OPR=15
OPR=20
OPR=25
OPR=30
OPR=35
OPR=40
SpecificFuelConsumption
Fig 8 Variations of Specific Fuel Consumption with TIT
The variations of the graphs are based on the input values
taken and the thermodynamic laws governed those equations.
The parametric analysis of the gas turbine cycle of the present
work, film cooling has been taken for the cooling of the
turbine blade to increase the life and better performance.
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.1
0.2
0.3
0.4
0.5
0.6
0.7
OPR=10
OPR=15
OPR=20
OPR=25
OPR=30
OPR=35
OPR=40
NetPower
Fig 9 Variations of Net Power with TIT
Figure 3 shows the variations of the thermal efficiency for
various turbine inlet temperature (TIT) at a given values of
atmospheric pressure, atmospheric temperature and overall
pressure ratio (OPR). It seems from the graph that the
efficiency increases with the increase in TIT for both type of
cycles i.e. for cooled turbine blade and uncooled turbine blade.
It has been observed that the thermal efficiency of the
uncooled turbine blade is slightly better that the one with
cooled turbine blade. It is due to fact that the temperature at
the inlet of the turbine is decreases. Figure 4 shows the
variations of m’c / m’g with TIT. The mass of coolant
required is calculated as the fraction of the exhaust gases. It
has been observed from the figure that the mass of coolant
required is limited up to first stator only at low turbine inlet
temperature but as long as the temperature increases, the
cooling required is in later stages as well. As shown in the
figure that for TIT 1800 and above, the cooling is must for at
least two stages. That is two stators and two rotors.
Figure 5 represents the variations of Thermal Efficiency with
TIT for an uncooled turbine blade for various overall pressure
ratios. The thermal efficiency increases on increasing the OPR
for higher range of TIT. At lower TIT, the thermal efficiency
is high for low OPR and it has little variation for the entire
range of TIT. Figure 6 represents the variations of Thermal
Efficiency with TIT for a cooled turbine blade for various
overall pressure ratios. Almost same variations have been
found in this graph also. Figure 7 shows the variations of
Work Ratio with TIT for various overall pressure ratios. For a
given value of OPR, the work ratio increases on increasing the
TIT. At a given TIT, the work ratio decreases on increasing
the OPR. Figure 8 shows the variations of Specific Fuel
Consumption (SFC) with TIT for various Overall pressure
ratios. SFC decreases on increasing the TIT for a given OPR.
At low OPR, this change is in a limited range but at higher
OPR it varies in wide range. Figure 9 shows the variations of
Net Power with TIT. Net power increases on increasing the
value of TIT. It has been observed that the net power
decreases on increasing the OPR for a given value of TIT.
Figure 10 represents the variations of Thermal Efficiency for
an uncooled turbine with TIT for various ambient
temperatures. Thermal efficiency increases on increasing the
TIT for a given value of ambient temperature. At low ambient
temperature the thermal efficiency is higher compared to high
ambient temperature. Figure 11 shows the variations of
Thermal Efficiency of a cooled gas turbine with TIT for
various ambient temperatures. It also has the same effect as
the uncooled turbine blade does. The difference in that, the
uncooled gas turbine has more efficiency that a cooled gas
turbine blade for a given ambient temperature.

__________________________________________________________________________________________
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.20
0.21
0.22
0.23
0.24
0.25
0.26
0.27
0.28
0.29
0.30
0.31
0.32
0.33
0.34
0.35
0.36
Thermal Efficiency without turbine blade cooling
Ta=280 K
Ta=290 K
Ta=300 K
Ta=310 K
Ta=320 K
Ta=330 K
ThermalEfficiencyWithoutTBC
Fig 10 Variations of Thermal Efficiency uncooled turbine
with TIT
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.12
0.14
0.16
0.18
0.20
0.22
0.24
0.26
0.28
0.30
0.32
0.34
Thermal Efficiency with turbine blade cooling
Ta=280 K
Ta=290 K
Ta=300 K
Ta=310 K
Ta=320 K
Ta=330 K
ThermalEfficiencywithTBC
Fig 11 Variations of Thermal Efficiency of cooled Turbine
with TIT
1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Pa=1.01325 bar
OPR=30
Ta=280 K
Ta=290 K
Ta=300 K
Ta=310 K
Ta=320 K
Ta=330 K
SpecificFuelConsumption
Fig 12 Variations of SFC with TIT
Figure 12 shows the variations of SFC with TIT for various
ambient temperatures. SFC decrease continuously on
increasing the TIT. It decreases steeply in the low range of
TIT but at the higher range of TIT, this variation is slightly
low. It also reflects that the maximum value of SFC is for high
ambient temperature. Figure 13 represents the variations of
mass of coolant required per kg of gas (m’c/m’g) with ambient
temperatures. The mass of cooling air required is increases on
increasing the ambient temperature. In the first stage of
turbine, the mass of coolant required is increases continuously
with the ambient temperature but in the second stage of
turbine the variation of coolant required is almost constant
with the ambient temperatures.
280 290 300 310 320 330
0.012
0.014
0.016
0.018
0.020
0.022
0.024
0.026
0.028
0.030
0.032
0.034
0.036
0.038
Pa=1.01325 bar
OPR=30
TIT=1500 K
1st Stator
1st Rotor
2nd Stator
(MassofCoolantRequired)m
'
c
/m
'
g
Atmospheric Temperature (K)
Fig 13 Variations of (m’c/m’g) with Ambient Temperatures
10 15 20 25 30 35 40
0.27
0.28
0.29
0.30
0.31
0.32
0.33
0.34
0.35
Pa=1.01325 bar
TIT=1500 K
Ta=280 K
Ta=290 K
Ta=300 K
Ta=310 K
Ta=320 K
Ta=330 K
ThermalEfficiencywithoutTBC
Overall Pressure Ratio
Fig 14 Variations of Thermal Efficiency of uncooled turbine
with OPR
Figure 14 represents the variations of thermal efficiency of an
uncooled turbine with OPR for various ambient temperatures.
It has been observed that, the thermal efficiency first increases
and then decreases on increasing the OPR for a given value of
ambient temperature. The thermal efficiency is higher for low
ambient temperature and also the thermal efficiency for this

__________________________________________________________________________________________
range of ambient temperature is continuously increases on
increasing the OPR.
10 15 20 25 30 35 40
0.220
0.225
0.230
0.235
0.240
0.245
0.250
0.255
0.260
0.265
0.270
0.275
0.280
0.285
0.290
0.295
0.300
Pa=1.01325 bar
TIT=1500 K
Ta=280 K
Ta=290 K
Ta=300 K
Ta=310 K
Ta=320 K
Ta=330 K
ThermalEfficiencywithTBC
Fig 15 Variations of Thermal Efficiency of cooled blade with
OPR
10 15 20 25 30 35 40
0.012
0.014
0.016
0.018
0.020
0.022
0.024
0.026
0.028
0.030
0.032
0.034
0.036
0.038
Pa=1.01325 bar
TIT=1500 K
Ta=300 K
m
'
c
/m
'
g
for 1st Stator
m
'
c
/m
'
g
for 1st Rotor
m
'
c
/m
'
g
for 2st Stator
MassofCoolantrequired(m
'
c
/m
'
g
)
Fig 16 Variations of (m’c/m’g) with OPR
Figure 15 shows the variations of thermal efficiency of a
cooled blade gas turbine with OPR for various ambient
temperatures. In this case, the natures of the curves are almost
similar to the previous graph. The difference is that, efficiency
is decreases for the entire range of the OPR after a slight
increase at the low range of OPR. Figure 16 shows the
variations of mass of coolant required (m’c/m’g) with OPR for
a given value of ambient temperature and turbine inlet
temperature. In the first stage of turbine, the mass of coolant
required is increases on increasing the OPR but for the second
stage the mass of coolant is required are decreases.
4. CONCLUSIONS
The gas turbine power plant has been analyzed for various
parameters. The most important parameter which has been
covered in this work is the new method of calculating the
coolant flow requirements for gas turbine blades especially at
higher temperatures. There are various types of cooling
method approach have already been published in various
literatures. In the present wok the film cooling has been taken
for the calculation of the blade cooling. It describes how the
cooling flow in each chordwise strip may be calculated,
assuming a particular internal cooling geometry. Comparisons
with a simplified method of calculation, assuming constant
blade temperature along the span, indicate broad agreement.
The new method presented should then give more reliable
evaluations than the semi-empirical methods, particularly for
the study of innovative cycles, where conventional fluids and
operating conditions cannot be assumed in the performance
calculations. It is hoped that such full development of the code
will provide a useful design tool for the turbine designer faced
with the necessity of blade cooling.
Table 1: Input parameters for calculation
S. No. Parameter Value
1 Atm. Press. 1.01325 bar
2 Turbine Efficiency 90%
3 Compressor Efficiency 90%
4 Mechanical Efficiency 99%
5 Mass of air flow 1 kg/s
6 Turbine Inlet Temp 1200-2000K
7 Overall Pressure Ratio 10-40
REFERENCES
[1]. Koff, B., Gas Turbine Technology Evolution: A
Designer's Perspective. Journal of Propulsion and Power, 2004
20(4): p. 577-595.
[2]. Tai, J. and e. al, University Research Engineering
Technology Institute (URETI) on Aeropropulsion and Power
Technology 2006, Georgia Institute of Technology.
[3]. Winstone, M., The Contribution of Advanced Nickel
Alloys to Future Aero-Engines. Journal of Defence Science
2000. 5(4): p. F65-F71.
[4]. Gauntner, J., Algorithm for Calculating Turbine Cooling
Flow and the Resulting Decrease in Turbine Efficiency,
N.L.R. Center, Editor. 1980, NASA: Cleveland, OH.
[5]. Esgar, J., R. Colladay, and A. Kaufman, An Analysis of
the Capabilities and Limitations of Turbine Air Cooling
Methods, N.L.R. Center, Editor. 1970, NASA: Cleveland, OH.
[6]. Torbidini, L. and A. Massardo, Analytical Blade Row
Cooling Model for Innovative Gas Turbine Cycle Evaluations
Supported by Semi-Empirical Air-Cooled Blade Data Journal
of Engineering for Gas Turbines and Power, 2004. 126: p.
498-506.
[7]. Vittal, S., P. Hajela, and A. Joshi, Review of Approaches
to gas turbine life management, in 10th AIAA/ISSMO
Multidisciplinary Analysis and Optimization. 2004, AIAA:
Albany, NY.
[8]. Horlock, J. H., Watson, D. T., and Jones, T. V., 2001,
“Limitations on Gas Turbine Performance Imposed by Large
Turbine Cooling Flows,” ASME J. Eng. Gas Turbines Power,
123, pp. 487–494.

__________________________________________________________________________________________
[9]. Thamir K. Ibrahim1*, M. M. Rahman1 and Ahmed N.
Abdalla2 Improvement of gas turbine performance based on
inlet air cooling systems: A technical review International
Journal of Physical Sciences Vol. 6(4), pp. 620-627, 18
February, 2011
[10]. Cun-liang Liu et al., “Film cooling performance of
converging slot-hole rows on a gas turbine blade”,
International Journal of Heat and Mass Transfer 53 (2010)
5232–5241
[11]. Sanjay Onkar Singh and B.N. Prasada, “Comparative
performance analysis of cogeneration gas turbine cycle for
different blade cooling means”, International Journal of
Thermal Sciences 48 (2009) 1432–1440
BIOGRAPHIES
Amjed Ahmed Jasim AL-Luhaibi born
on 8th Aug 1988 and completed B. Tech.
from Technical collage / Kirkuk in fuel
and energy engineering department,
Foundation of Technical Education, Iraq .
Currently pursuing M. Tech. in
Thermal engineering, Mechanical
engineering department Sam Higginbottom Institute of
Agriculture, Technology and Sciences (Formerly Allahabad
Agricultural Institute-Deemed University)
Dr. Mohammad Tariq, Assistant
Professor, Department of Mechanical
engineering, SSET, Sam Higginbottom
Institute of Agriculture, Technology and
Sciences (Formerly Allahabad
Agricultural Institute-Deemed
University), Allahabad, UP, India. I have
more than 14 years of academic experiences. About 20
articles/ papers have already been published in various
journals. More than 20 M. Tech. students have been
supervised. 5 students are doing Ph.D. under my supervision.

Thermal analysis of cooling effect on gas turbine blade

More Related Content

Thermal analysis of cooling effect on gas turbine blade