シンプレックス法
【英】:simplex method
概要
単体法と訳され, 1947年, ダンツィク(G.B. Dantzig) によって提案された,線形計画問題を解くための手法.理論的には有限回反復での収束性しか示されていないが,実用的には高速に最適解が得られることが知られている.また, 実用の際には, 単体法を改良した改訂単体法が良く用いられる.
詳説
ダンツイック(G. B. Dantzig)によって提案された単体法(simplex method)(シンプレックス法)は, カーマーカー法の出現する1984年までは線形計画問題を解くもっとも有効な解法とされていた. 単体法は問題の構造を巧妙に利用しており, いまでも, 線形計画, 整数計画, 組合せ最適化の多くの分野で使われている[2, 3, 4]. 以下, 次のような基準形と呼ばれる線形計画問題を考えることにする.
 |
ここで,  は実数,
は実数,  は
は 個の変数からなる
個の変数からなる 次元ベクトルである. すべての線形計問題は, 簡単な変換によって基準形に帰着できる. 問題(P)の制約条件を満たす
次元ベクトルである. すべての線形計問題は, 簡単な変換によって基準形に帰着できる. 問題(P)の制約条件を満たす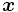 を実行可能解(feasible solution), その集まりを実行可能多面体(feasible polyhedron)と呼ぶ. 実行可能解のなかで目的関数を最大にするものを最適解(optimal solution)と呼ぶ.
を実行可能解(feasible solution), その集まりを実行可能多面体(feasible polyhedron)と呼ぶ. 実行可能解のなかで目的関数を最大にするものを最適解(optimal solution)と呼ぶ.
ここで, 問題(P)にスラック変数と呼ばれる非負の変数 を導入する
を導入する
 |
さらに, 目的関数を  と書き, 制約式左辺のスラック変数以外の項を移行すると, 上の問題は以下のようになる.
と書き, 制約式左辺のスラック変数以外の項を移行すると, 上の問題は以下のようになる.
|
|
制約式の左辺の変数を基底変数, 右辺の変数を非基底変数と呼ぶ. ここで, 非基底変数の添字を , 基底変数の添字を
, 基底変数の添字を とおき, 各変数の係数の添字も対応するものにする. 非基底変数の値を任意に固定すると基底変数の値は一意に定まるが, 特に非基底変数をすべて
とおき, 各変数の係数の添字も対応するものにする. 非基底変数の値を任意に固定すると基底変数の値は一意に定まるが, 特に非基底変数をすべて に固定して得られる解を基底解(basic solution)と呼ぶ. また, 上の等式系を辞書と呼ぶ. 係数
に固定して得られる解を基底解(basic solution)と呼ぶ. また, 上の等式系を辞書と呼ぶ. 係数 が非負のとき, 基底解は実行可能解であるが, このような辞書を実行可能辞書と呼ぶ. 線形計画問題の実行可能な基底解は実行可能多面体の頂点に対応する [3]. 単体法は目的関数の値を最大化する実行可能な基底解を求めるものであり, 辞書を等価な辞書へと繰り返し変換することによって実現される.
が非負のとき, 基底解は実行可能解であるが, このような辞書を実行可能辞書と呼ぶ. 線形計画問題の実行可能な基底解は実行可能多面体の頂点に対応する [3]. 単体法は目的関数の値を最大化する実行可能な基底解を求めるものであり, 辞書を等価な辞書へと繰り返し変換することによって実現される.
実行可能解をもつ問題に対して単体法が有限回で終了すれば, その問題は最適解をもつか, または非有界である. しかし, 辞書の右辺に の定数
の定数 を少なくとも1つ含むとき, 辞書は退化しており, 単体法は有限回で終わるとは限らない. このとき, ピボット演算を施しても, 基底解が変化しないことになり, 目的関数値も変化しない. 有限回収束を保証するための手段として, Blandのピボット選択規則 [1] が提案されており, これを用いると単体法は必ず有限回で収束する.
を少なくとも1つ含むとき, 辞書は退化しており, 単体法は有限回で終わるとは限らない. このとき, ピボット演算を施しても, 基底解が変化しないことになり, 目的関数値も変化しない. 有限回収束を保証するための手段として, Blandのピボット選択規則 [1] が提案されており, これを用いると単体法は必ず有限回で収束する.
先の説明で述べたように, 単体法の入力として実行可能な辞書が必要とされる. 現在の辞書が実行可能でない場合, 単体法を用いて実行可能な辞書を求めることができる. そのため, 新しい変数(人工変数)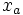 を用いて補助問題
を用いて補助問題
 |
を作る. 元問題が実行可能であることと補助問題の最適目的関数値が であることは等価なので, 補助問題を解くことにより, 元問題の実行可能解の有無を判定できる.
であることは等価なので, 補助問題を解くことにより, 元問題の実行可能解の有無を判定できる.
一般に, 基準形の線形計画問題を解く際には, 2段階単体法と呼ばれるものを用いる. 第1段階では, 補助問題を解き, 実行可能解の有無を判定し, 実行可能解が存在する場合は実行可能辞書を求める. 第2段階では, 求めた実行可能辞書を初期の辞書として, もう一度単体法を使い, 元問題を解く.
[1] R. G. Bland, "New finite pivot ruless for the simplex method", Mathematics of Operations Research 2(1977), 103-107.
[2] V. Chvátal, Linear Programming, W. H. Freeman and Company, 1983.
[3] G. B. Dantzig, Linear Programming and Extensions, Princeton Univesity Press, 1963.
[4] G. L. Nemhauser and L. A. Wolsey, Integer and Combinatorial Optimization, John Wiley & Sons, 1988.
単体法
【英】:simplex method
概要
1947年, ダンツィク(G.B. Dantzig) によって提案された,線形計画問題を解くための手法.理論的には有限回反復での収束性しか示されていないが,実用的には高速に最適解が得られることが知られている.また, 実用の際には, 単体法を改良した改訂単体法が良く用いられる.
詳説
ダンツイック(G. B. Dantzig)によって提案された単体法(simplex method)(シンプレックス法)は, カーマーカー法の出現する1984年までは線形計画問題を解くもっとも有効な解法とされていた. 単体法は問題の構造を巧妙に利用しており, いまでも, 線形計画, 整数計画, 組合せ最適化の多くの分野で使われている[2, 3, 4]. 以下, 次のような基準形と呼ばれる線形計画問題を考えることにする.
 |
ここで,  は実数,
は実数,  は
は 個の変数からなる
個の変数からなる 次元ベクトルである. すべての線形計問題は, 簡単な変換によって基準形に帰着できる. 問題(P)の制約条件を満たす
次元ベクトルである. すべての線形計問題は, 簡単な変換によって基準形に帰着できる. 問題(P)の制約条件を満たす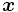 を実行可能解(feasible solution), その集まりを実行可能多面体(feasible polyhedron)と呼ぶ. 実行可能解のなかで目的関数を最大にするものを最適解(optimal solution)と呼ぶ.
を実行可能解(feasible solution), その集まりを実行可能多面体(feasible polyhedron)と呼ぶ. 実行可能解のなかで目的関数を最大にするものを最適解(optimal solution)と呼ぶ.
ここで, 問題(P)にスラック変数と呼ばれる非負の変数 を導入する
を導入する
 |
さらに, 目的関数を  と書き, 制約式左辺のスラック変数以外の項を移行すると, 上の問題は以下のようになる.
と書き, 制約式左辺のスラック変数以外の項を移行すると, 上の問題は以下のようになる.
|
|
制約式の左辺の変数を基底変数, 右辺の変数を非基底変数と呼ぶ. ここで, 非基底変数の添字を , 基底変数の添字を
, 基底変数の添字を とおき, 各変数の係数の添字も対応するものにする. 非基底変数の値を任意に固定すると基底変数の値は一意に定まるが, 特に非基底変数をすべて
とおき, 各変数の係数の添字も対応するものにする. 非基底変数の値を任意に固定すると基底変数の値は一意に定まるが, 特に非基底変数をすべて に固定して得られる解を基底解(basic solution)と呼ぶ. また, 上の等式系を辞書と呼ぶ. 係数
に固定して得られる解を基底解(basic solution)と呼ぶ. また, 上の等式系を辞書と呼ぶ. 係数 が非負のとき, 基底解は実行可能解であるが, このような辞書を実行可能辞書と呼ぶ. 線形計画問題の実行可能な基底解は実行可能多面体の頂点に対応する [3]. 単体法は目的関数の値を最大化する実行可能な基底解を求めるものであり, 辞書を等価な辞書へと繰り返し変換することによって実現される.
が非負のとき, 基底解は実行可能解であるが, このような辞書を実行可能辞書と呼ぶ. 線形計画問題の実行可能な基底解は実行可能多面体の頂点に対応する [3]. 単体法は目的関数の値を最大化する実行可能な基底解を求めるものであり, 辞書を等価な辞書へと繰り返し変換することによって実現される.
単体法
実行可能解をもつ問題に対して単体法が有限回で終了すれば, その問題は最適解をもつか, または非有界である. しかし, 辞書の右辺に の定数
の定数 を少なくとも1つ含むとき, 辞書は退化しており, 単体法は有限回で終わるとは限らない. このとき, ピボット演算を施しても, 基底解が変化しないことになり, 目的関数値も変化しない. 有限回収束を保証するための手段として, Blandのピボット選択規則 [1] が提案されており, これを用いると単体法は必ず有限回で収束する.
を少なくとも1つ含むとき, 辞書は退化しており, 単体法は有限回で終わるとは限らない. このとき, ピボット演算を施しても, 基底解が変化しないことになり, 目的関数値も変化しない. 有限回収束を保証するための手段として, Blandのピボット選択規則 [1] が提案されており, これを用いると単体法は必ず有限回で収束する.
先の説明で述べたように, 単体法の入力として実行可能な辞書が必要とされる. 現在の辞書が実行可能でない場合, 単体法を用いて実行可能な辞書を求めることができる. そのために, 新しい変数(人工変数)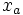 を用いて補助問題
を用いて補助問題
 |
を作る. 元問題が実行可能であることと補助問題の最適目的関数値が であることは等価なので, 補助問題を解くことにより, 元問題の実行可能解の有無を判定できる.
であることは等価なので, 補助問題を解くことにより, 元問題の実行可能解の有無を判定できる.
一般に, 基準形の線形計画問題を解く際には, 2段階単体法と呼ばれるものを用いる. 第1段階では, 補助問題を解き, 実行可能解の有無を判定し, 実行可能解が存在する場合は実行可能辞書を求める. 第2段階では, 求めた実行可能辞書を初期の辞書として, もう一度単体法を使い, 元問題を解く.
[1] R. G. Bland, "New finite pivot ruless for the simplex method", Mathematics of Operations Research 2(1977), 103-107.
[2] V. Chvátal, Linear Programming, W. H. Freeman and Company, 1983.
[3] G. B. Dantzig, Linear Programming and Extensions, Princeton Univesity Press, 1963.
[4] G. L. Nemhauser and L. A. Wolsey, Integer and Combinatorial Optimization, John Wiley & Sons, 1988.
シンプレックス法
(simplex method から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/08/24 09:42 UTC 版)
ナビゲーションに移動 検索に移動 |
シンプレックス法(英: simplex method、単体法)は、1947年にジョージ・ダンツィークが提案した、線型計画問題を解くアルゴリズムの中で最も広く使用されている方法である。線型計画法の1つ。
概要
シンプレックス法は、実行可能解 (超多面体の頂点) の1つから出発して目的関数の値をなるべく大きく (小さく) するようなところに移動させていく動作を繰り返して最適解を見つけ出す方法である。各ステップで必ず目的関数の値は改善される。
このアルゴリズムは、実用上は高速であり、変数の数・条件式の数の大きな方のオーダーの回数だけ反復を繰り返せばほとんど常に最適解に達する。このことは、1982年に スティーヴン・スメイル (Stephen Smale) が証明した。シンプレックス法は、用いるピボット規則により性能が左右される。有限回のピヴォットで終了することが保証されている規則として、Blandの提案した最小添字規則が知られている。Dantzigの提案したピボット規則は問題の規模にたいして指数時間かかる問題例があることが知られている。現在のところ、線型計画問題を多項式時間で解くピボット規則の存在性は未解決問題である。
単体法という名前は、Dantzig が提案した特殊な図解法においては、アルゴリズムの進行に従って単体が下に落ちていくように見えることに由来する。
アルゴリズム
 | この節の加筆が望まれています。 |
一般的な流れは以下のとおりである。
- 線型計画問題を制限標準型に変形する。
- スラック変数を加え、標準型に変形する。制約条件のうち、不等式を含む物がなくなり、全て等式となる。
- 人工変数を加え、制限標準型に変形する。等式化された問題の目的関数を z とおく。z を最大化 (最小化) する線型計画問題にする。
- ここまで行った作業を基にシンプレックス表 (Simplex Tableau、線型計画問題の係数を表にまとめたもの) を作成する。
- 式の数だけ基底変数を定める。目的関数zは必ず基底変数に選ばなければならない。
- 初期の基底変数から得られた連立方程式の解が最適かどうかを調べる。最適とみなすことができた場合は終了。終了しなかった場合は以下の作業をおこなう。
- 基底変数と非基底変数の組合せを変更する。
参考文献
- William H. Press(著)、William T. Vetterling(著)、Saul A. Teukolsky(著)、Brian P. Flannery(著)、丹慶 勝市(翻訳)、佐藤 俊郎(翻訳)、奥村 晴彦(翻訳)『ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ』技術評論社、1993年6月1日。ISBN 978-4874085608。
- 水野 眞治, 『シンプレックス法の巡回とその回避』
- 松井 知己, 『Bland の最小添字規則の有限性 -単体法の非巡回ピヴォット規則- 』
外部リンク
| ||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
「simplex method」の例文・使い方・用例・文例
- simplex methodのページへのリンク

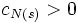 となる
となる を
を を
を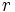 を
を だけをできる
だけをできる )を
)を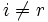 ) に
) に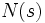 と
と を
を





