創刊号から先月号までPDFでお読みになれます。 お読みいただくには「Adobe Reader」が必要です。標準でPCにはインストール済みと思いますが、お持ちでない方は、http://get.adobe.com/jp/reader/からダウンロードしてインストールしてください。

「みんなの世界史」(世界史のまとめ/日本史のまとめ) noteコンテンツの総目次です。 全部合わせると、100万字以上あると思いますが、全文無料です。 since 2018.10- 基本コンセプト 昔と今を、今と未来をつなぐ。 世界の中の日本、日本の中の世界をつなぐ。 世界史を26ピースに「輪切り」にし、 深く、たのしく、わかりやすく”翻訳”する。 コンテンツの一覧【1】ゼロからはじめる世界史のまとめ(世界史×ゼロから) 【2】同時に学ぶ! 世界史と地理(世界史×地理) 【3】世界史のまとめ × SDGs(世界史×未来) 【4】"世界史のなかの" 日本史のまとめ(世界史×日本史) 【5】世界史の教科書を最初から最後まで(世界史×教科書) 【6】新科目「歴史総合」を読む(歴史総合) 【7】新科目「世界史探究」を読む(世界史探究) 【8】歴史の扉(歴史×モノ) 【9】歴史のことば(書評) 【1

『日本言語地図』(1966年〜1974年刊)は,全国各地の方言で,どのような語形や発音がどこに現れるかを項目ごとに表示した地図集です。 本ページでは,『日本言語地図』所載の全地図の画像をPDF形式で公開しています。 地図画像は縮刷版(1981年〜1985年刊)から作成しました。また、『日本言語地図』各集の別冊・付録は国立国語研究所学術情報リポジトリで閲覧・ダウンロードすることができます。 『日本言語地図』第1集~第2集の地図画像は クリエイティブ・コモンズ パブリック・ドメイン・マーク 1.0 ライセンスの下に提供されています。 『日本言語地図』第3集~第6集の地図画像は クリエイティブ・コモンズ 表示 4.0 国際 ライセンスの下に提供されています。 『日本言語地図』 第1集 言語地図 (50枚),参考地図 (1枚),付録A,付録B 『日本言語地図』第1集の地図画像は クリエイティブ・コ
「アラブ世界では代数学が発展した」とはよく聞くけど、どうも自分の中でしっくりきていなかったというか、要するにあんな難しいものがどうやって始まり発展したのだろう? と気になっていたのですが、最近思うのです。代数学の始まりとは、「イコールの学問」だったのではないか? と。 つまり、「ある数を2乗して1引いたら元の数と同じになるような数はあるかな?」とか、「1引いてから2乗したら元の数の2倍になるような数があったら面白そうじゃない?」みたいな素朴な疑問から始まったのではないかと思うのです。なにかの操作をした数と別の操作をした数が「同じ」、すなわちイコールの学問ではないかと。 これは現代の言葉で言えば前者は「」、後者は「」のことになります。これはまさに方程式です。「代数学が発展した」「方程式の学問が発展した」っていきなり言われても実感がわかないけど、こういう素朴な疑問から始まったとしたら、最初期の
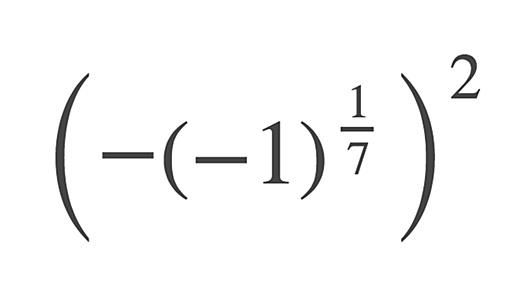
manavee.comは、2017年3月31日を以って、サービスの運営を終了いたしました。 【利用者の皆様へ】 利用者の皆様には、ご不便をおかけして申し訳ありません。 授業動画は、YouTube上で引き続き掲載しております。講義で前提になっている資料は、別のページで利用可能にしております。 しかし、授業動画を引き続き掲載するかどうかは、それぞれの先生の判断に委ねられておりますので、利用ができなくなる場合もございます。 どうぞご容赦ください。 NPO法人manavee代表理事 花房孟胤 【支援していただいた皆様へ】 本サービスについては、個人寄付、法人寄付をはじめとして、様々な形で応援していただきました。それは、本サービスの継続的な発展が期待されていたからであったと考えております。この度、manavee.comの運営を終了することで、そうした未来への可能性が閉ざされることになります。皆様の期
1. Nunokawa (2010) Nunokawa, K. (2010). Multiplication: introduction, 日本数学教育学会誌, No.92, Vol.11, pp.122-123. http://ci.nii.ac.jp/naid/110007994852 Students are required to clearly distinguish between multiplicands and multipliers at this stage because this distinction helps them understand the meaning of multiplication. Teachers pay attention to whether their students understand that multiplicands

かけ算の式の順序にこだわってバツを付ける教え方は止めるべきである 黒木玄 2012年12月24日更新 (2010年11月23日作成) (2015年11月4日に「ひとつあたり」を「一つ分」に置換した) ------------------------------------------------------------------------------ この文書は長過ぎるので以下の2つを最初に読んでおくと良いかもしれない。 掛順こだわり教育に関する資料[2012年10月17日] (中日新聞取材受諾メールに書いた資料) ベネッセの回答へのコメント (ベネッセによる回答のすべての段落にコメント) ------------------------------------------------------------------------------ ◇A59にまとめがあります。最初に読んで
This Domain Has Expired, To Renew Please Contact Your Provider.
先日の記事 誰もがどこかでつまずいた→小学校の算数から大学数学まで126の難所を16種類に分類した 読書猿Classic: between / beyond readers を読んだ人から「やりなおし魂に火をつけるだけつけて放置するのは無責任だ、何をやればいいのか教えろ」という問い合わせがあった。 小学校の算数レベルから微積分など高校+αまで、ついている予備テストをやれば、どの章は飛ばしていいか、どこの章のどの問題を勉強すればよいかを教えてくれる往年の名著(が復刻してた) を紹介しようと思ったが(科学を志さない人にも勧められる)、買い損なった場合と人のために、web上の教材をリストにして、先の記事の補いとする。 (2017.9.6 リンク切れ等、訂正しました) 小学校〜高校 小学校の算数 中学校の数学 高校数学 大学数学基礎 小学校〜高校 小学校「算数科」,中学校・高等学校「数学科」の内容

数学嫌いはどこから生まれてくるのか? よく聞かれる「役に立たないから」なる理由は、実のところ良くて後付け悪くて言い訳であって、その実態は、算数や数学につまずいて分からなくなった人たちが、イソップ寓話のキツネよろしく「あのブドウ(数学)は酸っぱい(役に立たない)」と言い広めているのである。 ならば撃つべきは〈算数・数学のつまずき〉である。 以下に示すのは、小学校の算数から大学基礎レベルの数学まで、「つまずいて分からなくなる」箇所を集めて16のカテゴリーに分類したものである。 一度もつまずかず専門レベルまで一気に駆け上がることのできた一握りの天才を除けば、数学が得意な人も不得意な人もみなどこかでつまずいたであろう、さまざまな算数・数学の難所が挙げられている。 この分類が示そうとしていることのひとつは、同じ〈根っこ〉をもったつまずきが、小・中・高・大の各レベルで繰り返し出現することである。 たと

その内うちの子用に必要になりそうなので、備忘録的に。 昔というのは十数年前。一応このやり方で、大体の子は三桁÷二桁の割り算の筆算ができるところまでもってこれてた。教職免許もちではないので、実際の教壇でどう教えるのかは知らない。 対象者は、「割り算の筆算が分からない」という子。対象年齢は小学校高学年、場合によっては中学校低学年。三桁÷二桁なのは、二桁×二桁の掛け算が出来るかどうかもついでに確認出来るから、というのが理由。 仮に、205÷17という割り算の問題を想定する。途中の掛け算がシンプルなのと、余りが1出るので教えやすい、というのが理由。当時も大体この式を使っていた。 前提その一。教え方をステップ化して、どこでつまづくかを確認する。全部一度に理解出来る子は、少なくとも私が教えた中では滅多にいなかった。また、小4くらいで算数が苦手な子は、かなり初歩でつまづいたままなんとなく放置している場合
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く