Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2025-01-01T20:44:55.941Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE STRUCTURE OF COMPUTABLE REDUCIBILITY ON EQUIVALENCE RELATIONS OF NATURAL NUMBERS

Part of: Computability and recursion theory

Published online by Cambridge University Press:  12 April 2022

URI ANDREWS ,
DANIEL F. BELIN  and
LUCA SAN MAURO
URI ANDREWS*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN MADISON, WI 53706-1388, USA E-mail: dbelin@wisc.edu
DANIEL F. BELIN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN MADISON, WI 53706-1388, USA E-mail: dbelin@wisc.edu
LUCA SAN MAURO
Affiliation:
DEPARTMENT OF MATHEMATICS “GUIDO CASTELNUOVO” SAPIENZA UNIVERSITY OF ROME ROME, ITALY E-mail: luca.sanmauro@uniroma1.it
*
E-mail: andrews@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the degree structure $\operatorname {\mathrm {\mathbf {ER}}}$ of equivalence relations on $\omega $ under computable reducibility. We examine when pairs of degrees have a least upper bound. In particular, we show that sufficiently incomparable pairs of degrees do not have a least upper bound but that some incomparable degrees do, and we characterize the degrees which have a least upper bound with every finite equivalence relation. We show that the natural classes of finite, light, and dark degrees are definable in $\operatorname {\mathrm {\mathbf {ER}}}$. We show that every equivalence relation has continuum many self-full strong minimal covers, and that $\mathbf {d}\oplus \mathbf {\operatorname {\mathrm {\mathbf {Id}}}_1}$ needn’t be a strong minimal cover of a self-full degree 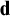$\mathbf {d}$. Finally, we show that the theory of the degree structure $\operatorname {\mathrm {\mathbf {ER}}}$ as well as the theories of the substructures of light degrees and of dark degrees are each computably isomorphic with second-order arithmetic.

Keywords

computable reducibilitycountable equivalence relationscomputably enumerable equivalence relationssecond-order arithmetic

MSC classification

Primary: 03D55: Hierarchies
Secondary: 03D30: Other degrees and reducibilities
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 3 , September 2023 , pp. 1038 - 1063
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, U., Badaev, S., and Sorbi, A.. A survey on universal computably enumerable equivalence relations , Computability and Complexity , Springer, Cham, 2017, pp. 418–451.10.1007/978-3-319-50062-1_25CrossRefGoogle Scholar
Andrews, U., Lempp, S., Miller, J. S., Ng, K. M., San Mauro, L., and Sorbi, A., Universal computably enumerable equivalence relations, this Journal, vol. 79 (2014), no. 1, pp. 60–88.Google Scholar
Andrews, U., Schweber, N., and Sorbi, A., Self-full ceers and the uniform join operator. Journal of Logic and Computation , vol. 30 (2020), no. 3, pp. 765–783.10.1093/logcom/exaa023CrossRefGoogle Scholar
Andrews, U., Schweber, N., and Sorbi, A., The theory of ceers computes true arithmetic. Annals of Pure and Applied Logic , vol. 171 (2020), no. 8, p. 102811.CrossRefGoogle Scholar
Andrews, U. and Sorbi, A., Joins and meets in the structure of ceers. Computability , vol. 8 (2019), nos. 3–4, pp. 193–241.CrossRefGoogle Scholar
Bard, V., Uniform martin’s conjecture, locally. Proceedings of the American Mathematical Society , vol. 148 (2020), no. 12, pp. 5369–5380.10.1090/proc/15159CrossRefGoogle Scholar
Bazhenov, N., Mustafa, M., San Mauro, L., Sorbi, A., and Yamaleev, M., Classifying equivalence relations in the Ershov hierarchy. Archive for Mathematical Logic , vol. 59 (2020), nos. 7–8, pp. 835–864.CrossRefGoogle Scholar
Bazhenov, N. A., Mustafa, M., San Mauro, L., and Yamaleev, M. M., Minimal equivalence relations in hyperarithmetical and analytical hierarchies. Lobachevskii Journal of Mathematics , vol. 41 (2020), no. 2, pp. 145–150.10.1134/S199508022002002XCrossRefGoogle Scholar
Bernardi, C. and Sorbi, A., Classifying positive equivalence relations, this Journal, vol. 48 (1983), no. 03, pp. 529–538.Google Scholar
Coskey, S., Hamkins, J. D., and Miller, R., The hierarchy of equivalence relations on the natural numbers under computable reducibility. Computability , vol. 1 (2012), no. 1, pp. 15–38.10.3233/COM-2012-004CrossRefGoogle Scholar
Ershov, Y. L., Teoriya Numeratsii , Nauka, Moscow, 1977.Google Scholar
Ershov, Y. L., Theory of numberings , Handbook of Computability Theory (Griffor, E. G., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North-Holland, Amsterdam, 1999, pp. 473–503.10.1016/S0049-237X(99)80030-5CrossRefGoogle Scholar
Fokina, E., Rossegger, D., and San Mauro, L., Measuring the complexity of reductions between equivalence relations. Computability , vol. 8 (2019), nos. 3–4, pp. 265–280.CrossRefGoogle Scholar
Fokina, E. B., Friedman, S.-D., Harizanov, V., Knight, J. F., McCoy, C., and Montalbán, A., Isomorphism relations on computable structures, this Journal, vol. 77 (2012), no. 1, pp. 122–132.Google Scholar
Gao, S., Invariant Descriptive Set Theory , CRC Press, Boca Raton, FL, 2008.CrossRefGoogle Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence relations. Studia Logica , vol. 67 (2001), pp. 27–59.10.1023/A:1010521410739CrossRefGoogle Scholar
Hjorth, G., Borel equivalence relations , Handbook of Set Theory , Springer, Dordrecht, 2010, pp. 297–332.CrossRefGoogle Scholar
Ianovski, E., Miller, R., Ng, K. M., and Nies, A., Complexity of equivalence relations and preorders from computability theory, this Journal, vol. 79 (2014), no. 3, pp. 859–881.Google Scholar
Lavrov, I. A., Effective inseparability of the set of identically true formulas and the set of formulas with finite counterexamples for certain elementary theories. Algebra Logika , vol. 2 (1962), pp. 5–18.Google Scholar
Nerode, A. and Shore, R. A., Second Order Logic and First Order Theories of Reducibility Orderings , Studies in Logic and the Foundations of Mathematics, vol. 101, Elsevier, Amsterdam, 1980, pp. 181–200.Google Scholar
Ng, K. M. and Hongyuan, Y., On the degree structure of equivalence relations under computable reducibility. Notre Dame Journal of Formal Logic , vol. 60 (2019), no. 4, pp. 733–761.CrossRefGoogle Scholar
Simpson, S. G., First-order theory of the degrees of recursive unsolvability. Annals of Mathematics , vol. 105 (1977), no. 1, pp. 121–139.CrossRefGoogle Scholar
Slaman, T. A. and Woodin, W. H., Definability in the enumeration degrees. Archive for Mathematical Logic , vol. 36 (1997), nos. 4–5, pp. 255–267.CrossRefGoogle Scholar
Soare, R. I., Turing Computability: Theory and Applications , Springer, Berlin, 2016.CrossRefGoogle Scholar