Coherent transient exciton transport in disordered polaritonic wires

3.1 Polariton-mediated exciton wave packet propagation

Selected wave packet snapshots are given in Figure 2, along with the corresponding time-dependent exciton RMSD, P _M , and migration probability χ. The main effect of static disorder can be observed in these examples. From Figure 2a–c, as disorder is increased, the wave packet mobility is significantly reduced, and its spread is strongly suppressed. Simultaneously, we find the photonic content and its time-dependent fluctuations monotonically decrease and become small under strong disorder (e.g., P _M (t) is relatively stable around 0.97 when σ _M /Ω _R = 100 %). In contrast, photon content fluctuations are large under weak disorder (σ _M /Ω _R → 0). The effect of disorder on photon content fluctuations may be directly understood from Rabi oscillations, which occur unperturbed at weak disorder while being strongly damped as σ _M approaches Ω _R [33]. These observations illustrate how the oscillatory energy exchange between radiation and matter leads to enhanced coherent exciton transport. Since we are examining very large values of disorder (σ _M /Ω _R ≥ 100 %), we include in our SI (Section 8) an analysis of how the signatures of strong light–matter coupling change under increasingly stronger static disorder.

Figure 2:

Average exciton wave packet profiles at different time delays and relative disorder strength (σ _M /Ω _R ) of 5 %, 20 %, and 100 % for (a), (b) and (c), respectively. Probabilities are grouped in bins containing 50 dipoles spanning 0.5 μm. P _M , RMSD, and χ are defined in Equations (8)–(10), respectively. In all cases, Ω _R = 0.1 eV and σ _x = 120 nm.

In Figure 3, the average exciton migration probability (Equation (10)) and RMSD are shown for excitons propagating over 4 ps under different values of relative disorder strength (σ _M /Ω _R ). The migration probability, seen in Figure 3a, increases rapidly before achieving a steady state (dχ(t)/dt ≈ 0) around 2 ps irrespective of the disorder strength. Conversely, disorder plays a crucial role in the sub-300 fs phase of the dynamics, where we find from the inset that in all considered cases, an increase in σ _M leads to a slower initial exciton migration. From the behavior of χ(t) at large t, we find the steady-state exciton migration probability at weak disorder is largely suppressed when σ _M is increased. Nevertheless, the strongly disordered cases (σ _M /Ω _R ≥ 1) suggest that beyond a particular disorder strength, χ(t ≫ 0) becomes approximately independent of σ _M . Figures S6 and 7 provide χ(t) for Ω _R = 0.2 eV and Ω _R = 0.3 eV under different levels of disorder and verify the disorder effects on χ(t) described above are in fact generic.

Figure 3:

Propagation of exciton wave packets at different disorder strengths measured by (a) migration probability (Equation (10)) and (b) RMSD (Equation (8)). The dotted lines in (b) are linear fits of the early propagation (<500 fs) from which slopes are used to measure the initial ballistic velocity (v ₀). Insets show a zoomed-in view into the sub 500-fs region. In all cases, Ω _R = 0.1 eV and σ _x = 120 nm.

In the SI Section 2, we show the initial growth of χ(t) can be approximated in the weak and strong disorder limits by analyzing the disorder-averaged properties of |⟨0; n|ψ(t)⟩|². This leads to the conclusion that ∂χ(t)/∂t → 0 as t → 0⁺, so that the quantity G = (1/2)∂² χ(t)/∂t ², t → 0⁺ controls the early growth of χ(t). In the weak and strong disorder limits, G satisfies, respectively

where A and B are eigenstates, A _n and B _n the probability amplitude to detect an exciton at the nth dipole when the system is in the A and B eigenstates, respectively, I = [ n min , n max ] (see Equation (10) and accompanying description), N I is the number of sites in I , c _n is the nth exciton amplitude in the initial wave packet, and f ̄ is the disorder average of quantity f. Both approximations to G, in the weakly and strongly disordered regimes suggest ultrafast increase in the exciton migration probability depends on the existence of eigenstates with large energy differences and significant contributions from the dipoles comprising the initial wave packet.

From Equation (12), we infer (i) the steep increase of χ(t) at early times is enhanced by raising Ω _R at fixed energetic disorder (as the energy difference between polariton modes formed from near-resonant photon and excitons increase with Ω _R ) and (ii) increasing disorder with fixed Ω _R leads to initial slower growth of χ t → 0 + , due to the greater tendency of localization of the nth exciton into strongly localized eigenmodes. Importantly, while the summand of Equation (11) has the same form as that of Equation (12), the former has several more non-negligible contributions than the latter ( N I 2 in the approximation given in Equation (11)), and therefore, a much steeper early increase occurs in χ(t) under weak disorder.

In summary, as measured by χ(t), indeed, disorder slows down the ability of excitons to migrate at very early times, and increasing the Rabi splitting leads to faster initial migration probability for dipoles in photonic wires. Similar considerations can be made on the asymptotic (t → ∞) behavior of χ(t): disorder averaging and the lack of correlation between the excitation energy at distinct sites suppresses cross-terms in the strong disorder limit relative to weak and, therefore, a reduced σ _M favors a larger steady-state value of χ(t). Additionally, Figure 3a suggests a steady-state time for χ(t) that is almost independent of disorder. This contrasts with the RMSD behavior shown in Figure 3b, implying that the approximately disorder-independent χ(t) steady-state times correspond to a feature specific to the nonstandard observable χ(t). For the rest of this manuscript, we characterize the transport velocity using the RMSD; therefore, we leave a detailed analysis of χ(t) for future studies.

The RMSD measure reported in Figure 3b also indicates that the excitonic propagation is fastest in the fs time scale. Both χ(t → ∞) and RMSD(t → ∞) drop when the σ _M /Ω _R is increased from 20 % to 40 %. However, comparing the 40 % and 100 % relative disorder strength cases in Figure 3b, we note the emergence of a disorder-enhanced transport regime (DET) as reported in previous studies of dipole chains under strong light–matter interactions [31], [33], [34], [40]. This DET regime clearly leaves no signature in χ(t) (Figure 3a) but may be understood based on earlier studies of exciton transport in a polaritonic wire. In this regime, weakly coupled states are expected to be exponentially localized but can have slowly decreasing extended tails [31], [34]. These tails carry a small probability away from the initial excitation spot and contribute to the greater RMSD values reported with increasing σ _M /Ω _R . Conversely, the extended tails associated with DET leave no signature in χ(t), as this quantity only tracks the probability in the bulk of the wave packet. These points are corroborated by Figures S3–5 of the SI, where we show the decay profile of wave packets and the emergence of the extended tails responsible for DET.

We reinforce that the asymptotic behavior seen in both Figure 3a and b can be attributed to Anderson localization and not to finite-size artifacts. To demonstrate that, we show in Figure S1 the shape of the wave packets at long propagation times, whereas Figure S2 reveals that, under sufficiently strong disorder, the exciton probability at x ₀ ± L _x /2 (i.e., where periodic boundary conditions are enforced) remains negligible throughout the simulation.

In Figure 3b, dotted lines represent linear fits obtained from the first 500 fs of simulation. This initial linear behavior (minimum coefficient of determination R ² = 0.98) characterizes the excitonic ballistic spread. In the next sections, we will use this value as a measure of the initial exciton spread velocity (v ₀). Our choice of a 500-fs time interval aimed to average out complicated features at very early times and to avoid localization effects observed around 1 ps. We checked that all reported qualitative trends are unaffected by a choice of initial time interval that satisfies the described conditions (see Figures S10–12 for a comparison of v ₀ obtained using different initial time intervals).

The existence of a short-lived ballistic regime even under strong disorder (σ _M /Ω _R ≥ 1) is a generic feature of sufficiently narrow wave packets. It follows from the fact that the nth exciton probability at early times t → 0 is given by P _n (t) ≈ P _n (0) + a _n t ², where a _n is a site-dependent constant [41]. Therefore, RMSD²(t) at sufficiently small t is equal to RMSD²(0) + ∑ n ( x n − x 0 ) 2 a n t 2 . Hence, there is a short time frame where RMSD(t) = RMSD 2 ( 0 ) + c t 2 , where c = ∑ n ( x n − x 0 ) 2 a n . If RMSD(0) is small enough, then there exists a short time interval RMSD(t) is proportional to t regardless of the amount of disorder.

To conclude this subsection, we note the polariton-mediated ultrafast exciton transport described here shows intriguing differences relative to bare exciton transport analyzed in a recent study by Cui et al. [35]. Their work showed that transient ultrafast energy transfer mediated by direct short-range interactions benefits from the existence of static disorder, leading to faster transport (relative to a perfectly ordered system) in the femtosecond timescale. Cui et al. ascribe their observation of transient disorder enhancement of transport to the suppression of destructive interference induced by the heterogeneity of the matter excitation energies [35]. Here, we find the opposite feature: disorder always reduces the initial transport velocity. Even in the DET regime, Figure 3b shows a narrow window at early times where transport is subdiffusive [33]. This contrast points toward a fundamental difference in how static disorder affects direct and polariton-mediated coherent exciton transport.

3.2 Ballistic exciton transport

In Figure 4, the initial exciton spread velocity (v ₀) is shown as a function of relative disorder σ _M /Ω _R . We examine v ₀ obtained for systems with variable collective light–matter interaction strength Ω _R (with fixed relative disorder σ _M /Ω _R ) and two selected initial wave packet sizes (σ _x in Equation (6)). In both cases, we observe an initial steep decay of v ₀ with increasing σ _M /Ω _R , which is followed by a plateau until the DET regime is reached at σ _M /Ω _R ≈ 1. However, a salient difference in the variation of v ₀ with Ω _R at low disorder is observed between the narrow (σ _x = 120 nm) and the broader (σ _x = 480 nm) wave packets in Figure 4a and b, respectively. This difference vanishes quickly when disorder is increased, demonstrating the initial state preparation is less important to the dynamics under strong disorder. Nevertheless, the distinct Ω _R dependence of v ₀ is observable in a sizable range of disorder strengths (0 ∼ 30 %), thereby warranting a mechanistic explanation. We pursue that by analyzing below the (excitonic) spread velocity of the wave packet in the absence of disorder.

Figure 4:

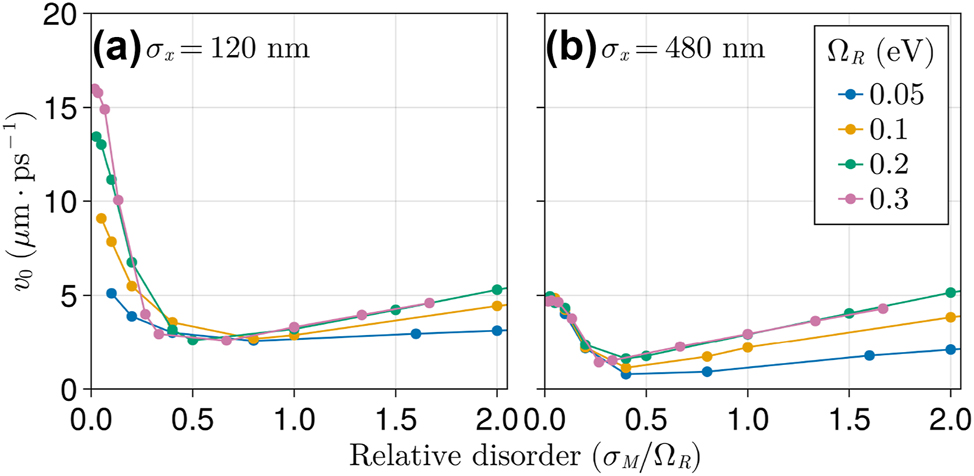
Initial ballistic velocity (v ₀) for various wave packets with a (a) narrow and (b) broad initial spread values (σ _x , see Equation (6)). v ₀ was computed as the slope of a linear fit of RMSD values in the initial 500 fs of simulation (see Figure 3).

The detailed mathematical treatment of the spread velocity, which we summarize below, is provided in Section 1 of the SI. We first emphasize that the treatment of the ballistic transport regime is unconventional even in the zero-disorder case because (a) our initial wave packets range from strongly localized (σ _x = 120 nm) to moderately delocalized (σ _x = 480 nm) in real space, (b) the wave packet has LP and UP components, and (c) the polariton dispersion is not quadratic. These features imply the basic treatment of Gaussian wave packet transport in a quadratic medium, generally valid for sufficiently narrow wave packets in q-space, is inapplicable [42]. With these considerations, we show (see SI) that the dominant contribution to the exciton transport velocity v ₀ is given by

where P(q) is the t = 0 exciton probability distribution in q-space. From Equation (7), the width σ _q of P(q) is inversely proportional to the real-space width of the initial wave packet σ _x . The effective group velocity v α q eff (where α is UP or LP) is defined as

where Π _αq is the total exciton content of the polariton mode α with wave number q, and ∂ ω α q ∂ q is the (conventional) group velocity v g α q of the same mode. The polaritonic group velocity weighted by the corresponding exciton content Π _αq yields the effective exciton group velocity v α q eff of mode α q . The total matter content Π _αq plays a key role because even though high energy regions of the UP branch yield the largest v g α q , their small Π _αq results in negligible v α q eff values. From Equation (13) one can see that v ₀ is controlled by the effective group velocity v α q eff weighted by the exciton P(q) distribution. Hence, as we demonstrate below, the different ways P(q) and v α q eff overlap explain the varying mobility of differently prepared excitons in weakly and moderately disordered systems.

Effective group velocities v α q eff for systems with Ω _R = 0.1 and Ω _R = 0.2 eV are presented with an overlay of P(q) for several initial exciton wave packets in Figure 5. The first relevant observation is the substantial increase of v α q eff with Ω _R for both α = LP and UP with q > 0.003 nm⁻¹. The Rabi splitting does not affect the effective group velocity for polariton modes with q < 0.003 nm⁻¹. This feature explains the Rabi splitting dependence of v ₀ observed in Figure 4b in weakly and moderately disordered systems. Specifically, a broad wave packet in real space (e.g., σ _x = 480 nm) is narrow in q-space and is only non-vanishing at a small interval of q near zero (the wave packet center in q space) where v α q eff is nearly identical for all values of Ω _R examined here. Therefore, as seen in Figure 4b, sufficiently broad wave packets show no significant dependence on Ω _R when σ _M /Ω _R is not too large (up to 40 % in Figure 4).

Figure 5:

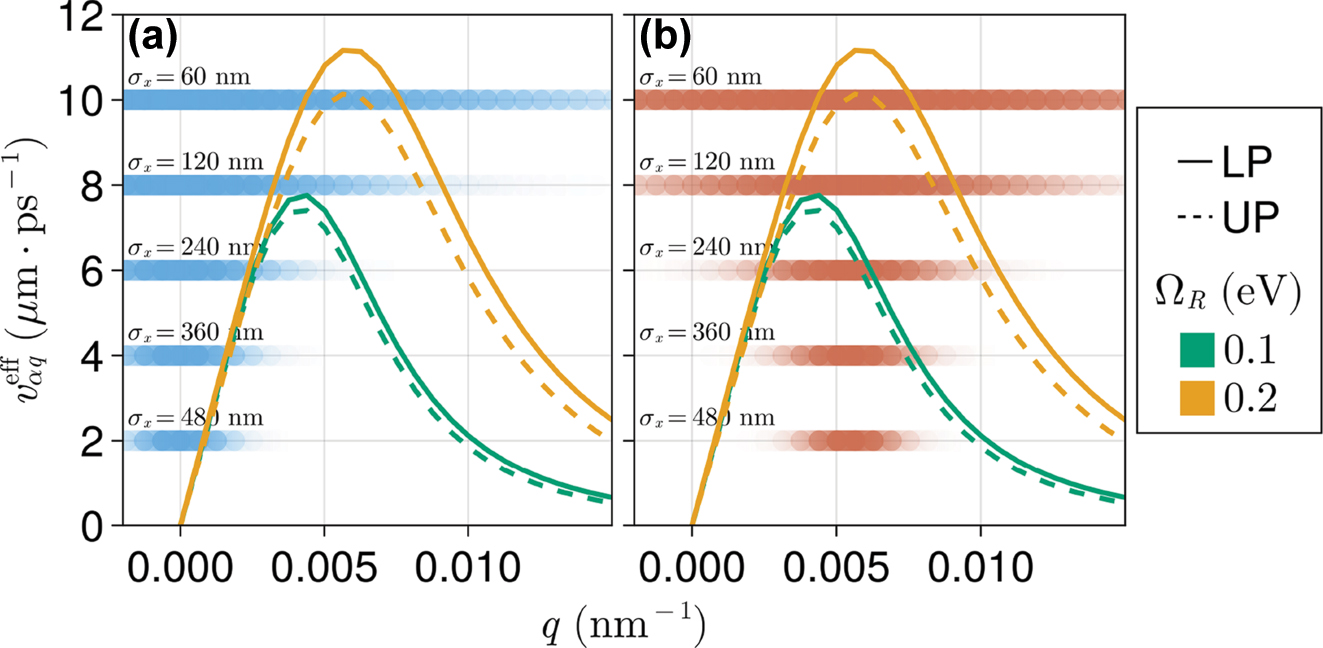
Effective group velocity (Equation (14)) for different values of Ω _R . Horizontal gradient bars represent the P(q) distribution for different exciton wave packets (see Equation (6)) with (a) q ̄ 0 = 0.0 and (b) q ̄ 0 = 0.0055 nm⁻¹. The overlap between the gradient bars (P(q)) and the v α q eff curves yields the exciton ballistic velocity v ₀ (Equation (13)). See text for more details.

In Figure 6, we present quantitative evidence that Equations (13) and (14) appropriately describe the early-time exciton wave packet propagation rate under small and moderate disorder conditions. In particular, Figure 6 shows v ₀ versus σ _x at various relative disorder strengths (σ _M /Ω _R ). As shown in Figure 6a, in almost every case considered, when the initial state has zero average momentum ( q ̄ 0 = 0 ) , an increase in σ _x results in a slower propagation. This generic behavior at weak and moderate disorder can be readily understood from Figure 5a and b. As σ _x broadens, the width of the P(q) distribution (centered at q ̄ 0 = 0 ) is reduced, and v ₀ decreases due to the increasing dominance of contributions with small effective group velocities in Equation (13).

Figure 6:

Initial ballistic velocity (v ₀) dependency on the wave packet initial spread (σ _x ) with: (a) q ̄ 0 = 0 and (b) q ̄ 0 = 0.0056 nm⁻¹. Gray dotted curves are values obtained from Equation (13).

The gray dotted curves in Figure 6 follow from Equation (13). This equation not only captures the overall qualitative trend at small and moderate disorder but also reproduces the local maximum at σ _x = 120 nm in Figure 6a. This peak can be explained again based on Figure 5: by increasing the wave packet width in q-space, polariton components with larger v α q eff become relevant and v ₀ (Equation (13)) increases, but if P(q) becomes too broad (e.g., σ _x = 60 nm), polaritons with smaller v α q eff (with q greater than the maxima in v α q eff ) start to contribute significantly to v ₀ (at the expense of high exciton group velocity components) leading to an overall reduction in the magnitude of v ₀.

Figure 6b shows analogous results for an exciton prepared with q ̄ 0 = 0.005654 nm⁻¹. Indeed, in this case, broader wave packets display higher mobility than narrow ones as measured by v ₀. This is expected based on Equations (13) and (14) as here a smaller uncertainty in q (increased σ _x ) localizes P(q) around q ≈ q ̄ 0 ≠ 0 where the corresponding v α q eff values are appreciable (see Figure 5b). Overall, these results give a simple prescription to optimize polariton-mediated coherent exciton transport by preparing a sufficiently broad initial state (large σ _x and small σ _q ) with average momentum ( q ̄ 0 ) centered at the maximum of v α q eff .

Note that polariton states no longer have well-defined q values in the presence of nonvanishing disorder, and strictly speaking, the arguments above based on uncertainty relations break down. However, in Figure 6, this breakdown is only observed when σ _M /Ω _R = 1.0, where v ₀ is nearly independent of σ _x . Our analysis in terms of uncertainty relations and Equations (13) and (14) is seen to hold qualitatively for σ _M /Ω _R < 40 %, indicating that the model presented here can be used for examination of coherent exciton transport at early times even in systems with moderate disorder.

To conclude, we investigate the effect of light–matter detuning δ = ℏω ₀ − E _M on polariton-assisted exciton propagation. This study is motivated by detuning being a simple controllable microcavity parameter [1] and by previous work, which reported greater steady-state exciton migration probability under negative detuning (red-shifted cavities, where E _M > ℏω ₀) [43]. We investigate the early dynamics in detuned microcavities by computing v ₀ for a variable E _M and fixed cavity lowest-energy mode ℏω ₀ = 2.0 eV. To gain insight into the long-time properties of the wave packet, we also show the maximum RMSD value observed over 5 ps.

In Figure 7, we find detuning effects on v ₀ and the maximum RMSD are very similar. Under weak disorder (σ _M /Ω _R < 0.4), both v ₀(δ) and RMSD(δ) are peaked at δ = 0, i.e., the coherent exciton motion is faster when the cavity is in resonance with the dipolar excitation. This can be rationalized with Figure 8a, which shows a strong dependence of v α q eff on detuning. Blue-shifted microcavities lead to the slowest exciton motion as evidenced by the consistently smaller v α q eff obtained for δ = 0.2 eV in Figure 8. On the other hand, red-shifted microcavities have small v α q eff at q close to zero but higher values (compared to the resonant cavity) at sufficiently large q. Since the initial wave packets of Figure 7 have q ̄ 0 = 0 , the dominant polariton contributions to the evolution are those for which v α q eff is larger at zero-detuning in comparison to the red-shifted case. Nevertheless, comparison between v α q eff at zero and negative detuning in Figure 8b suggests that polariton-mediated exciton wave packet transport can be much faster in red-shifted cavities when the initial-state is prepared with q ̄ 0 close to the maximum of v α q eff . Indeed, we show numerical results in our supporting information (Figure S13) that confirm this prediction.

Figure 7:

Disorder-dependent detuning effects on coherent exciton transport measured by (a) the initial spread velocity (v ₀) and (b) the maximum RMSD over 5 ps. In all cases, Ω _R = 0.1 eV and σ _x = 240 nm.

Figure 8:

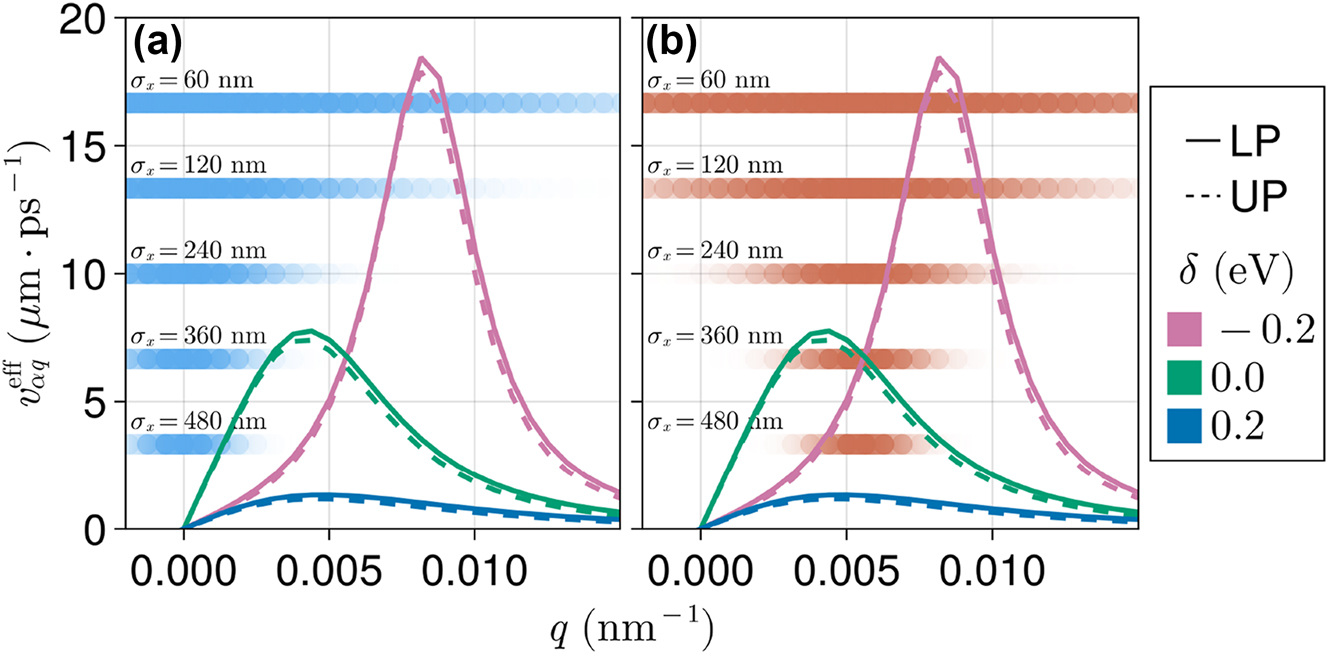
Effective group velocity (Equation (14)) for variable detuning δ = ℏω ₀ − E _M . Horizontal gradient bars represent the P(q) distribution for distinct exciton wave packets (see Equation (6)) with (a) q ̄ 0 = 0.0 and (b) q ̄ 0 = 0.0055 nm⁻¹. The overlap between the gradient bars (P(q)) and the v α q eff curves yields the exciton spread velocity v ₀ (Equation (13)). See text for more details.

In the presence of stronger disorder (σ _M > 0.4Ω _R ), Figure 7 shows the condition δ = 0 no longer provides a maximum RMSD and v ₀, and the optimal detuning value is shifted toward negative values. Therefore, under sufficient disorder, red-shifting the microcavity enhances the exciton ballistic transport and the transport distance regardless of the initial wave packet preparation. This feature may be understood by noting that in the presence of a significant amount of static disorder, many dipoles will have excitation energies below the lowest-energy microcavity mode. In this case, it becomes advantageous to employ negative detuning, since it supports lower energy photon modes that can interact resonantly with the dipoles with lower excitation energy. Conversely, raising ℏω ₀ − E _M to positive values leads to a reduction in the light–matter spectral overlap and, therefore, the maximum RMSD and v ₀ consistently decrease as the microcavity is blue-shifted (δ > 0). Despite an optimum not being visible in Figure 7, we show in Figure S14 that both v ₀ and the maximum RMSD reach a plateau between δ = −1 eV and δ = −2 eV. However, we highlight that under such extreme values of negative detuning, the energy gap between the dipole excitation (E _M ) and higher photonic bands (e.g., n _y = 1, n _z = 2 and vice-versa) is about the same as the gap between the dipole excitation and the lowest photon mode (q = 0, n _y = n _z = 1). In this case, higher energy photon bands may start contributing to the dynamics just as much as EM modes in the n _y = n _z = 1 band. Therefore, a systematic analysis at large negative detunings must include multiple microcavity bands. We present these results here as they show a well-defined theoretical limit for the employed single-band model.

3.3 Losses and dynamical disorder

We finalize our discussion by offering brief considerations of how the exciton transport phenomena examined in this article would be affected by photon leakage and dynamical disorder (e.g., represented by time-dependent stochastic fluctuations of excitonic transition energies, dipole orientations, or intersite distances).

Photon leakage through imperfect mirrors is an unavoidable characteristic of physics in optical microcavities [1]. However, the impact of photon losses on the polariton-assisted exciton transport discussed here is minimal, especially at moderate and large disorder. Under these conditions, the typical time-dependent photon content is small enough (see Figure 2 and S1) that wave packet decay by photon loss is a slow process. For example, if the empty cavity photon lifetime is 50 fs, the corresponding wave packet lifetime is at least one or two orders of magnitude bigger, depending on its photonic content. Therefore, while cavity leakage could prevent observation of DET and subsequent Anderson localization in moderate and strongly disordered systems, the ultrafast ballistic regime would be almost unaffected.

In the weakly disordered scenario where photon content fluctuations can reach a significant value (Figure 2 and S1), the fast decay of the wave packet would prevent efficient energy transport. Nevertheless, even in this case, incorporation of cavity losses is unlikely to change the main qualitative trends observed for v ₀ as this quantity is computed at ultrafast times (e.g., Figures S10–12 show that the behavior of v ₀ with varying disorder and Rabi splitting is independent of the linear fit cutoff time).

The interplay between static and dynamical disorder is an interesting topic that we aim to address in detail in future work. Here, we simply point out some expected effects of dynamical disorder on the examined polariton-assisted exciton transport. First, dynamical disorder suppresses Rabi oscillations and may slow down the relatively efficient ultrafast exciton transport we observe at weak disorder. On the other hand, recent work by Cui and Nitzan has shown that dynamical disorder boosts the early-time exciton transport [35]. Further, it is well known that dynamical disorder prevents Anderson localization and leads to diffusive behavior at long times [41]. The latter behavior is generic so we expect it to persist in the moderate and strong (static) disorder regimes of polariton-assisted exciton transport. A recent study [32] suggests that excitonic interaction with a dynamical (finite-temperature) environment shortens the ballistic transport regime time interval and leads to a quick crossover to diffusive behavior. We expect similar features will emerge when dynamical disorder is incorporated into our model, but future work is necessary to determine the interplay between the effects of static and dynamical disorder in the investigated polariton-assisted exciton transport.