Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction
Abstract
:1. Introduction
2. Proposed Method
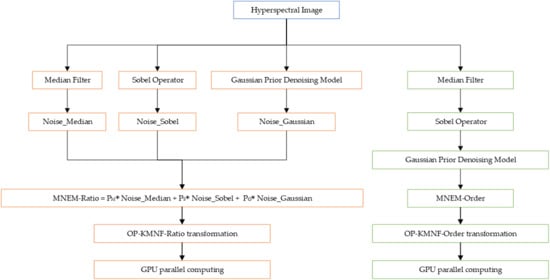
2.1. Mixed Noise Estimation Model
| Algorithm 1. The procedure of determining and in MENM-Ratio |
| Input: hyperspectral image Y. |
| Step 1: input Y into the median filter to obtain the median filter denoised image Y_Median. |
| Step 2: Sobel operator is used in Y to get the Sobel denoised image Y_DeNoise_Sobel = Y − Y_Sobel. |
| Step 3: Y is input into the Gaussian prior denoising model to obtain the denoised image Y_Gaussian. |
| Step 4: calculate the MSAD values , and between the input image and the denoised images Y_Median, Y_DeNoise_Sobel and Y_Gaussian. |
| Step 5: take the reciprocals, that is , and . |
| Step 6: , and . |
| Output: the values of and . |
2.2. Optimized Kernel Minimum Noise Fraction (OP-KMNF) Transformation
| Algorithm 2. The procedure of OP-KMNF-Ratio |
| Input: hyperspectral image Y |
| Step 1: input Y into the median filter to obtain Y_Median, and then Noise_Median = Y − Y_Median. |
| Step 2: Sobel operator is used in Y to get Noise_Sobel = Y_Sobel. |
| Step 3: Y is input into the Gaussian prior denoising model to obtain Y_Gaussian, and then Noise_Gaussian = Y − Y_Gaussian. |
| Step 4: noise estimation: MNEM-Ratio=PM × Noise_Median+ PS × Noise_Sobel + PG × Noise_Gaussian. |
| Step 5: transformation and kernelization of noise fraction according to Equation (10). |
| Step 6: calculate the eigenvectors of , and obtain the matrix of b. |
| Step 7: map all pixels onto the transformation matrix using Equation (14). |
| Output: hyperspectral image feature extraction result . |
| Algorithm 3. The procedure of OP-KMNF-Order |
| Input: hyperspectral image Y |
| Step 1: input Y into the median filter to obtain Y_Median. |
| Step 2: Sobel operator is used in Y_Median to get Noise_Sobel, and then Y_Sobel = Y_Median + Noise_Sobel. |
| Step 3: Y_Sobel is input into the Gaussian prior denoising model to obtain Y_Gaussian, and then MNEM-Order = Y − Y_Gaussian. |
| Step 4: transformation and kernelization of noise fraction according to Equation (10). |
| Step 5: calculate the eigenvectors of , and obtain the matrix of b. |
| Step 6: map all pixels onto the transformation matrix using Equation (14). |
| Output: hyperspectral image feature extraction result . |
2.3. Graphics Processing Units (GPU)-Based Parallel Computing
3. Results
3.1. Input Data
3.1.1. Salinas Dataset
3.1.2. Indian Pines Dataset
3.1.3. Xiong’an Dataset
3.2. Experiments on Noise Estimation
3.3. Experiments on OP-KMNF
3.4. Adaptability of OP-KMNF to Hyperspectral Images with Different Spatial Resolutions
3.5. Adaptability of OP-KMNF to Hyperspectral Images with Different Spectral Resolutions
3.6. GPU Implementation of OP-KMNF
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Gao, L.; Du, Q.; Zhang, B.; Yang, W.; Wu, Y. A Comparative study on linear regression-based noise estimation for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 488–498. [Google Scholar] [CrossRef] [Green Version]
- Jia, J.; Wang, Y.; Chen, J.; Guo, R.; Shu, R.; Wang, J. Status and application of advanced airborne hyperspectral imaging technology: A review. Infrared Phys. Technol. 2020, 104, 103115. [Google Scholar] [CrossRef]
- Bruce, L.; Koger, C.; Li, J. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, L.; Liao, W.; Zhang, B. A new kernel method for hyperspectral image feature extraction. Geospat. Inf. Sci. 2017, 20, 309–318. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Dimension Reduction Using Spatial and Spectral Regularized Local Discriminant Embedding for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1082–1095. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Xia, Y.; Xun, L.; Yan, Q.; Zhang, D. Class-Probability Based Semi-Supervised Dimensionality Reduction for Hyperspectral Images. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 September 2018; pp. 460–463. [Google Scholar]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Mutual-information-based semi-supervised hyperspectral band selection with high discrimination, high information, and low redundancy. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2956–2969. [Google Scholar] [CrossRef]
- Chen, W.; Yang, Z.; Cao, F.; Yan, Y.; Wang, M.; Qing, C.; Cheng, Y. Dimensionality reduction based on determinantal point process and singular spectrum analysis for hyperspectral images. IET Image Process. 2019, 13, 299–306. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef] [Green Version]
- Bajcsy, P.; Groves, P. Methodology for hyperspectral band selection. Photogramm. Eng. Remote Sens. 2004, 70, 793–802. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Su, H.; Sheng, Y. An efficient method for supervised hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2010, 8, 138–142. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Su, H.; Du, Q.; Chen, G.; Du, P. Optimized hyperspectral band selection using particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2659–2670. [Google Scholar] [CrossRef]
- Martínez-Usómartinez-Uso, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Clustering-based hyperspectral band selection using information measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K.; Le Moan, S. BandClust: An unsupervised band reduction method for hyperspectral remote sensing. IEEE Geosci. Remote Sens. Lett. 2010, 8, 565–569. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, J.; Gong, M. Unsupervised hyperspectral band selection by fuzzy clustering with particle swarm optimization. IEEE Geosci. Remote Sens. Lett. 2017, 14, 773–777. [Google Scholar] [CrossRef]
- Li, J.-M.; Qian, Y.-T. Clustering-based hyperspectral band selection using sparse nonnegative matrix factorization. J. Zhejiang Univ. Sci. C 2011, 12, 542–549. [Google Scholar] [CrossRef]
- Li, S.; Qi, H. Sparse Representation-Based Band Selection for Hyperspectral Images. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 2693–2696. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, L.; Du, B.; Li, W.; Lai, Y.M. Band selection using improved sparse subspace clustering for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2784–2797. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Y.; Zhao, Z. Optimal Band Selection for Hyperspectral Image Classification Based on Inter-Class Separability. In Proceedings of the 2010 Symposium on Photonics and Optoelectronics, Chengdu, China, 19–21 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Sildomar, T.-M.; Yukio, K. A Particle Swarm Optimization-Based Approach for Hyperspectral Band Selection. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3335–3340. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef] [Green Version]
- Berry, M.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef] [Green Version]
- Casalino, G.; Gillis, N. Sequential dimensionality reduction for extracting localized features. Pattern Recognit. 2017, 63, 15–29. [Google Scholar] [CrossRef] [Green Version]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Roger, R.E. Principal Components transform with simple, automatic noise adjustment. Int. J. Remote Sens. 1996, 17, 2719–2727. [Google Scholar] [CrossRef]
- Green, A.; Berman, M.; Switzer, P.; Craig, M. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.; Kuo, B.-C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Wong, W.K.; Zhao, H. Supervised optimal locality preserving projection. Pattern Recognit. 2012, 45, 186–197. [Google Scholar] [CrossRef]
- Roweis, S.T. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P.; Jiao, L.; Liu, F.; Gou, S.; Zhao, J.; Zhao, Z. Dimensionality reduction of hyperspectral imagery using sparse graph learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1165–1181. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Müller, K.-R. Kernel Principal Component Analysis. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin, Germany, 1997; pp. 583–588. [Google Scholar]
- Nielsen, A.A. Kernel maximum autocorrelation factor and minimum noise fraction transformations. IEEE Trans. Image Process. 2010, 20, 612–624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gillis, N.; Plemmons, R.J. Sparse nonnegative matrix underapproximation and its application to hyperspectral image analysis. Linear Algebra Appl. 2013, 438, 3991–4007. [Google Scholar] [CrossRef]
- Bachmann, C.; Ainsworth, T.; Fusina, R. Exploiting manifold geometry in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 441–454. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Nielsen, A.A.; Camps-Valls, G. Explicit Signal to Noise Ratio in Reproducing Kernel Hilbert Spaces. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3570–3573. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Vestergaard, J.S. Parameter Optimization in the Regularized Kernel Minimum Noise Fraction Transformation. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 370–373. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, B.; Chen, Z.; Lei, L. Study on the Issue of Noise Estimation in Dimension Reduction of Hyperspectral Images. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, L.; Zhang, B. An Optimized Method of Kernel Minimum Noise Fraction for Dimensionality Reduction of Hyperspectral Imagery. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 48–51. [Google Scholar] [CrossRef]
- Nielsen, A.A. An Extension to a Filter Implementation of a Local Quadratic Surface for Image Noise Estimation. In Proceedings of the 10th International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; pp. 119–124. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Du, Q.; Yang, W.; Zhang, B. A Comparative Study on Noise Estimation for Hyperspectral Imagery. In Proceedings of the 4th Workshop on Hyperspectral Image and Signal Processing, Shanghai, China, 4–7 June 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, B.; Sun, X.; Li, S.; Du, Q.; Wu, C. Optimized maximum noise fraction for dimensionality reduction of Chinese HJ-1A hyperspectral data. EURASIP J. Adv. Signal Process. 2013, 2013, 65. [Google Scholar] [CrossRef] [Green Version]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Huang, Z.; Huang, X.; Luo, F.; Ye, R. An adaptive nonlocal gaussian prior for hyperspectral image denoising. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1487–1491. [Google Scholar] [CrossRef]
- Sullivan, R. Introduction; Greenleaf Publishing Limited: Sheffield, UK, 2013; pp. 13–20. [Google Scholar]
- Xie, T.; Li, S.; Sun, B. Hyperspectral images denoising via nonconvex regularized low-rank and sparse matrix decomposition. IEEE Trans. Image Process. 2019, 29, 44–56. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y.; Wang, Y.; Wang, D.; Peng, C.; He, G. Denoising of hyperspectral images using nonconvex low rank matrix approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5366–5380. [Google Scholar] [CrossRef]
- Fykse, E. Performance Comparison of GPU, DSP and FPGA Implementations of Image Processing and Computer Vision Algo-rithms in Embedded Systems. Ph.D. Thesis, Department of Electronic Systems, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Fowers, J.; Brown, G.; Wernsing, J.; Stitt, G. A performance and energy comparison of convolution on GPUs, FPGAs, and multicore processors. ACM Trans. Arch. Code Optim. 2013, 9, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Barrachina, S.; Castillo, M.; Igual, F.D.; Mayo, R.; Quintana-Orti, E.S. Evaluation and Tuning of the Level 3 CUBLAS for Graphics Processors. In Proceedings of the 22nd IEEE International Parallel & Distributed Processing Symposium, Miami, FL, USA, 14–18 April 2008; pp. 1–8. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Bientinesi, P.; Gunnels, J.A.; Myers, M.E.; Quintana-Ortí, E.S.; Van De Geijn, R.A. The science of deriving dense linear algebra algorithms. ACM Trans. Math. Softw. 2005, 31, 1–26. [Google Scholar] [CrossRef]
- Fujimoto, N. Faster Matrix-Vector Multiplication on GeForce 8800GTX. In Proceedings of the 2011 IEEE International Parallel & Distributed Processing Symposium, Anchorage, AK, USA, 16–20 May 2008; pp. 1–8. [Google Scholar]
- Barrachina, S.; Castillo, M.; Igual, F.D.; Mayo, R.; Quintana-Ortí, E.S.; Quintana-Ortí, G. Exploiting the capabilities of modern GPUs for dense matrix computations. Concurr. Comput. Pract. Exp. 2009, 21, 2457–2477. [Google Scholar] [CrossRef]
- Jia, J.; Wang, Y.; Cheng, X.; Yuan, L.; Zhao, D.; Ye, Q.; Zhuang, X.; Shu, R.; Wang, J. Destriping algorithms based on statistics and spatial filtering for visible-to-thermal infrared pushbroom hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4077–4091. [Google Scholar] [CrossRef]
- Jia, J.; Zheng, X.; Guo, S.; Wang, Y.; Chen, J. Removing stripe noise based on improved statistics for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Cen, Y.; Zhang, L.; Zhang, X.; Wang, Y.; Qi, W.; Tang, S.; Zhang, P. Aerial hyperspectral remote sensing classification dataset of Xiong’an new area (Matiwan Village). J. Remote Sens. 2020, 24, 1299–1306. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Wang, Y. Preflight spectral calibration of airborne shortwave infrared hyperspectral imager with water vapor absorption characteristics. Sensors 2019, 19, 2259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.; Yuan, L.; Wang, S.; Yu, H.; Zhang, C.; He, D.; Han, G.; Wang, J.; Wang, Y. Wide swath and high resolution airborne hyperspectral imaging system and flight validation. Sensors 2019, 19, 1667. [Google Scholar] [CrossRef] [Green Version]
















| Parameter | GeForce GTX 745 | GeForce RTX 2060 |
|---|---|---|
| CUDA Cores | ||
| Global Memory | 4096 MBytes | 6144 MBytes |
| Shared Memory | 49,152 bytes | 49,152 bytes |
| Constant Memory | 65,536 bytes | 65,536 bytes |
| Clock Rate | 1.03 GHz | 1.20 GHz |
| Memory Bus Width | 128 bit | 192 bit |
| Method | MPSNR | MSSIM | MSAD |
|---|---|---|---|
| Salinas | |||
| KMNF-NE | 38.43 | 0.9889 | 2.3579 |
| SSDC | 33.73 | 0.9377 | 8.1005 |
| MNEM-Order | 26.97 | 0.9734 | 2.3828 |
| MNEM-Ratio | 43.69 | 0.9985 | 0.4701 |
| Indian Pines | |||
| KMNF-NE | 29.78 | 0.9487 | 2.1644 |
| SSDC | 26.47 | 0.8793 | 6.0796 |
| MNEM-Order | 46.29 | 0.9794 | 0.1983 |
| MNEM-Ratio | 29.76 | 0.9519 | 0.5402 |
| Xiong’an | |||
| KMNF-NE | 33.58 | 0.9785 | 2.0654 |
| SSDC | 37.86 | 0.9864 | 0.8181 |
| MNEM-Order | 43.71 | 0.9787 | 0.5339 |
| MNEM-Ratio | 36.96 | 0.9907 | 1.3098 |
| Classes | Salinas | Classes | Indian Pines | ||
|---|---|---|---|---|---|
| Samples | Training | Samples | Training | ||
| Broccoli_green_weeds_1 | 2009 | 502 | Alfalfa | 46 | 12 |
| Broccoli_green_weeds_2 | 3726 | 932 | Corn_notill | 1428 | 357 |
| Fallow | 1976 | 494 | Corn_mintill | 830 | 208 |
| Fallow_rough_plow | 1394 | 349 | Corn | 237 | 59 |
| Fallow_smooth | 2678 | 670 | Grass_pasture | 483 | 121 |
| Stubble | 3959 | 990 | Grass_trees | 730 | 183 |
| Celery | 3579 | 895 | Grass_pasture_mowed | 28 | 7 |
| Grapes_untrained | 11,271 | 2818 | Hay_windrowed | 478 | 120 |
| Soil_vineyard_develop | 6203 | 1551 | Oats | 20 | 5 |
| Corn_senesced_green_weeds | 3278 | 820 | Soybean_notill | 972 | 243 |
| Lettuce_romaine_4wk | 1068 | 267 | Soybean_mintill | 2455 | 614 |
| Lettuce_romaine_5wk | 1927 | 482 | Soybean_clean | 593 | 148 |
| Lettuce_romaine_6wk | 916 | 229 | Wheat | 205 | 51 |
| Lettuce_romaine_7wk | 1070 | 268 | Woods | 1265 | 316 |
| Vineyard_untrained | 7268 | 1817 | Buildings_Grass_Trees_Drives | 386 | 97 |
| Vineyard_vertical_trellis | 1807 | 452 | Stone_Steel_Towers | 93 | 23 |
| Classes | Samples | Training |
|---|---|---|
| Corn | 84,496 | 21,124 |
| Soybean | 10,562 | 2641 |
| Pear_trees | 1303 | 326 |
| Grassland | 27,703 | 6926 |
| Sparsewood | 9292 | 2323 |
| Robinia | 25,761 | 6440 |
| Paddy | 30,029 | 7507 |
| Populus | 5534 | 1384 |
| Sophora japonica | 811 | 203 |
| Peach_trees | 1498 | 375 |
| Salinas | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Features | 3 | 4 | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| PCA | 82.04 2.13 | 85.07 1.50 | 86.53 0.95 | 90.54 1.71 | 90.93 1.55 | 90.85 1.71 | 91.02 1.75 | 91.23 1.57 | 91.22 1.44 |
| MNF | 88.42 1.44 | 89.15 1.64 | 89.22 1.44 | 92.30 0.97 | 92.80 ± 1.22 | 92.74 1.62 | 92.59 1.65 | 92.53 ± 1.59 | 92.40 1.69 |
| OMNF | 88.55 ± 1.30 | 89.27 1.55 | 89.31 1.31 | 92.30 1.17 | 92.78 1.30 | 92.74 1.60 | 92.54 1.66 | 92.42 1.79 | 92.29 1.85 |
| FA | 85.87 0.21 | 89.04 1.58 | 89.02 1.63 | 91.66 1.65 | 92.15 1.78 | 92.01 2.08 | 93.12 1.44 | 93.80 0.97 | 93.76 0.84 |
| KPCA | 86.14 0.61 | 88.37 0.67 | 88.48 0.84 | 90.26 ± 1.61 | 90.85 1.75 | 91.09 1.87 | 91.37 1.84 | 91.45 1.96 | 91.40 1.95 |
| KMNF | 88.42 1.44 | 89.15 ± 1.64 | 89.22 1.44 | 92.30 0.97 | 92.80 1.22 | 92.74 1.62 | 92.60 1.64 | 92.54 1.58 | 92.41 1.68 |
| OKMNF | 87.32 1.19 | 88.55 1.13 | 88.43 1.05 | 92.01 1.14 | 92.97 1.32 | 93.21 1.29 | 93.25 1.31 | 93.59 1.46 | 93.66 1.26 |
| LDA | 86.27 1.84 | 86.72 1.47 | 88.61 1.85 | 90.79 2.12 | 91.46 1.96 | 91.37 1.88 | 91.35 1.83 | 91.49 1.51 | 91.48 ± 1.53 |
| LPP | 86.30 0.96 | 88.86 1.43 | 89.22 1.43 | 91.36 2.28 | 91.94 1.90 | 92.05 2.00 | 91.91 1.88 | 91.88 1.81 | 91.85 2.04 |
| OP-KMNF-Ratio | 87.25 0.46 | 91.12 1.62 | 91.64 1.70 | 93.92 1.16 | 94.25 1.20 | 94.50 1.36 | 94.63 1.59 | 94.61 1.72 | 94.69 1.81 |
| OP-KMNF-Order | 89.86 0.45 | 90.80 1.66 | 90.66 1.44 | 93.27 0.98 | 94.02 1.21 | 94.36 1.62 | 94.23 1.64 | 94.12 1.59 | 94.09 1.67 |
| Indian Pines | |||||||||
| Number of Features | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| PCA | 36.45 3.49 | 43.97 3.43 | 44.92 1.79 | 44.83 1.46 | 49.87 1.05 | 52.91 2.93 | 53.65 1.98 | ||
| MNF | 55.33 0.04 | 57.84 1.32 | 58.88 0.79 | 59.66 2.25 | 60.97 0.85 | 61.85 1.38 | 60.94 2.20 | ||
| OMNF | 54.49 0.59 | 57.06 1.40 | 58.40 1.06 | 59.38 2.59 | 60.97 1.70 | 61.83 1.21 | 60.94 1.91 | ||
| FA | 47.14 0.52 | 54.49 0.94 | 55.94 0.59 | 57.40 3.57 | 59.22 2.67 | 61.41 0.12 | 61.13 1.54 | ||
| KPCA | 36.36 0.63 | 39.69 0.61 | 41.55 0.69 | 43.85 0.76 | 47.01 0.23 | 47.60 0.12 | 52.86 0.42 | ||
| KMNF | 52.25 1.18 | 55.05 0.70 | 55.83 1.38 | 58.54 0.43 | 56.87 0.09 | 58.38 0.04 | 60.90 2.30 | ||
| OKMNF | 32.67 0.42 | 43.99 1.79 | 43.51 1.75 | 46.30 0.31 | 49.55 1.68 | 51.30 2.17 | 54.47 2.10 | ||
| LDA | 31.92 0.98 | 39.32 0.12 | 49.51 1.83 | 52.44 0.28 | 54.86 1.15 | 54.90 0.60 | 55.57 1.17 | ||
| LPP | 36.55 0.68 | 42.49 0.26 | 44.94 1.32 | 55.86 5.62 | 54.76 3.73 | 58.20 2.78 | 59.26 0.62 | ||
| OP-KMNF-Ratio | 56.00 0.19 | 58.54 0.20 | 59.54 0.64 | 55.99 0.35 | 56.54 1.36 | 60.80 1.04 | 60.71 0.87 | ||
| OP-KMNF-Order | 53.72 0.20 | 57.25 1.04 | 56.88 0.08 | 61.50 1.47 | 61.79 0.52 | 61.90 0.29 | 62.98 1.27 | ||
| Xiong’an | |||||||||
| Number of Features | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| PCA | 31.05 1.78 | 31.70 1.91 | 36.03 2.64 | 36.82 2.97 | 37.00 2.75 | 44.25 3.04 | 46.36 1.94 | ||
| MNF | 38.12 0.45 | 51.98 1.37 | 55.93 2.62 | 60.17 1.69 | 62.83 0.85 | 64.11 1.95 | 67.03 0.90 | ||
| OMNF | 38.15 0.51 | 53.39 ± 1.47 | 58.54 2.63 | 60.01 1.77 | 62.94 0.81 | 63.98 1.98 | 66.91 0.88 | ||
| FA | 40.39 2.56 | 51.82 1.94 | 54.59 2.14 | 57.03 1.55 | 57.88 1.24 | 58.74 0.97 | 59.54 1.14 | ||
| KPCA | 29.60 2.54 | 34.12 1.40 | 34.75 1.90 | 34.83 1.64 | 35.58 1.71 | 37.97 1.77 | 38.34 1.65 | ||
| KMNF | 43.82 2.30 | 51.27 2.16 | 54.37 2.40 | 58.61 1.56 | 61.71 2.15 | 60.57 1.87 | 63.38 2.11 | ||
| OKMNF | 39.42 1.74 | 53.34 1.32 | 58.98 1.48 | 59.61 1.66 | 61.41 2.17 | 63.18 0.85 | 65.71 0.83 | ||
| LDA | 37.57 2.35 | 40.93 3.65 | 42.25 3.21 | 43.00 1.11 | 44.94 2.31 | 49.51 2.18 | 55.88 2.19 | ||
| LPP | 30.03 1.13 | 41.48 3.86 | 46.29 3.96 | 47.75 4.06 | 52.96 3.69 | 53.21 2.32 | 54.35 2.05 | ||
| OP-KMNF-Ratio | 43.99 2.02 | 54.03 1.69 | 58.47 1.46 | 61.42 0.99 | 64.42 1.30 | 68.03 0.52 | 70.14 0.23 | ||
| OP-KMNF-Order | 48.36 0.98 | 54.32 1.20 | 59.53 2.95 | 61.73 0.75 | 62.38 1.42 | 65.60 2.16 | 67.35 1.97 | ||
| Classes | Corn | Soybean | Pear_Trees | Grassland | Sparsewood | Robinia | Paddy | Populus | Sophora Japonica | Peach_Trees |
|---|---|---|---|---|---|---|---|---|---|---|
| PCA | 69.72 | 28.10 | 51.11 | 39.88 | 8.09 | 69.22 | 63.74 | 13.28 | 29.10 | 91.32 |
| MNF | 79.33 | 88.54 | 77.13 | 65.15 | 47.18 | 78.34 | 75.48 | 23.49 | 48.46 | 87.25 |
| OMNF | 79.25 | 88.62 | 76.90 | 64.94 | 46.86 | 78.37 | 75.39 | 23.40 | 48.09 | 87.25 |
| FA | 74.98 | 76.97 | 73.98 | 46.20 | 29.60 | 75.40 | 66.89 | 25.03 | 36.00 | 90.39 |
| KPCA | 69.17 | 19.63 | 37.68 | 33.76 | 3.95 | 69.06 | 50.52 | 6.27 | 0.00 | 93.32 |
| KMNF | 77.40 | 83.59 | 77.21 | 61.32 | 44.64 | 77.21 | 59.73 | 31.91 | 31.44 | 89.32 |
| OKMNF | 76.54 | 83.13 | 74.52 | 52.80 | 40.17 | 83.32 | 77.75 | 32.62 | 47.84 | 88.38 |
| LDA | 73.54 | 73.69 | 70.22 | 43.43 | 22.31 | 70.98 | 72.47 | 29.80 | 12.08 | 90.25 |
| LPP | 71.13 | 63.98 | 73.98 | 46.16 | 30.28 | 68.72 | 67.16 | 32.06 | 0.00 | 89.99 |
| OP-KMNF (Ratio) | 78.17 | 87.67 | 75.98 | 52.60 | 44.19 | 80.54 | 81.14 | 42.84 | 69.30 | 88.99 |
| 1Rank 2Improve | 3 −1.16 | 3 −0.87 | 4 −1.23 | 5 −12.55 | 4 −2.99 | 2 −2.77 | 1 +3.39 | 1 +10.22 | 1 +20.84 | 7 −4.33 |
| OP-KMNF (Order) | 79.42 | 84.65 | 76.82 | 45.35 | 44.07 | 83.42 | 76.39 | 43.02 | 48.71 | 91.66 |
| Rank Improve | 1 +0.09 | 3 −3.89 | 4 −0.39 | 7 −19.80 | 5 −3.11 | 1 +0.10 | 2 −1.36 | 1 +10.40 | 1 +0.25 | 2 −1.66 |
| Classes | Spatial_Resolution_1 (0.5 m) | Spatial_Resolution_2 (1 m) | Spatial_Resolution_3 (2 m) | |||
|---|---|---|---|---|---|---|
| Samples | Training | Samples | Training | Samples | Training | |
| Corn | 84,496 | 21,124 | 20,728 | 5182 | 4925 | 1231 |
| Soybean | 10,562 | 2641 | 2474 | 618 | 523 | 130 |
| Pear_trees | 1303 | 326 | 312 | 78 | 71 | 18 |
| Grassland | 27,703 | 6926 | 6734 | 1683 | 1583 | 396 |
| Sparsewood | 9292 | 2323 | 2254 | 563 | 534 | 133 |
| Robinia | 25,761 | 6440 | 6274 | 1568 | 1508 | 377 |
| Paddy | 30,029 | 7507 | 7364 | 1841 | 1761 | 440 |
| Populus | 5534 | 1384 | 1345 | 336 | 318 | 80 |
| Sophora japonica | 811 | 203 | 182 | 45 | 36 | 9 |
| Peach_trees | 1498 | 375 | 348 | 87 | 73 | 18 |
| Classes | Spectral_Resolution_1 (2.4 nm) | Spectral _Resolution_2 (4.8 nm) | Spectral _Resolution_3 (9.6 nm) | |||
|---|---|---|---|---|---|---|
| Samples | Training | Samples | Training | Samples | Training | |
| Corn | 84,496 | 21,124 | 84,496 | 21,124 | 84,496 | 21,124 |
| Soybean | 10,562 | 2641 | 10,562 | 2641 | 10,562 | 2641 |
| Pear_trees | 1303 | 326 | 1303 | 326 | 1303 | 326 |
| Grassland | 27,703 | 6926 | 27,703 | 6926 | 27,703 | 6926 |
| Sparsewood | 9292 | 2323 | 9292 | 2323 | 9292 | 2323 |
| Robinia | 25,761 | 6440 | 25,761 | 6440 | 25,761 | 6440 |
| Paddy | 30,029 | 7507 | 30,029 | 7507 | 30,029 | 7507 |
| Populus | 5534 | 1384 | 5534 | 1384 | 5534 | 1384 |
| Sophora japonica | 811 | 203 | 811 | 203 | 811 | 203 |
| Peach_trees | 1498 | 375 | 1498 | 375 | 1498 | 375 |
| Data Sizes | CPU Runtime | GPU1 Runtime | Speedups1 | GPU2 Runtime | Speedups2 |
|---|---|---|---|---|---|
| OP-KMNF-Order | |||||
| 100 × 100 × 250 | 307.730 s | 20.924 s | 14.92× | 12.251 s | 25.12× |
| 150 × 150 × 250 | 678.703 s | 30.373 s | 22.35× | 17.352 s | 39.11× |
| 200 × 200 × 250 | 1177.293 s | 44.535 s | 26.44× | 23.923 s | 49.21× |
| 250 × 250 × 250 | 1837.850 s | 63.312 s | 29.03× | 34.143 s | 53.83× |
| 300 × 300 × 250 | 2627.564 s | 85.893 s | 30.59× | 45.275 s | 58.04× |
| 350 × 350 × 250 | 3586.769 s | 113.238 s | 31.67× | 58.944 s | 60.85× |
| 400 × 400 × 250 | 4682.999 s | 142.582 s | 32.84× | 73.232 s | 63.95× |
| OP-KMNF-Ratio | |||||
| 100 × 100 × 250 | 317.973 s | 21.906 s | 14.52× | 12.511 s | 25.42× |
| 150 × 150 × 250 | 704.654 s | 32.255 s | 21.85× | 18.161 s | 38.80× |
| 200 × 200 × 250 | 1234.365 s | 46.222 s | 26.71× | 24.101 s | 51.22× |
| 250 × 250 × 250 | 1918.372 s | 66.053 s | 29.04× | 34.686 s | 55.31× |
| 300 × 300 × 250 | 2742.355 s | 88.857 s | 30.86× | 46.064 s | 59.53× |
| 350 × 350 × 250 | 3739.979 s | 119.276 s | 31.36× | 59.001 s | 63.39× |
| 400 × 400 × 250 | 4877.802 s | 151.954 s | 32.10× | 75.891 s | 64.27× |
| Program × Execution | OP-KMNF-Order | OP-KMNF-Ratio | ||||
|---|---|---|---|---|---|---|
| CPU Runtime | GPU1 Runtime | GPU2 Runtime | CPU Runtime | GPU1 Runtime | GPU2 Runtime | |
| Data reading | 29.342 s | 29.342 s | 3.365 s | 29.342 s | 29.342 s | 3.365 s |
| Noise estimation | 2300.203 s | 82.571 s | 61.605 s | 2471.537 s | 91.206 s | 63.606 s |
| KMNF transformation | 2402.198 s | 13.804 s | 4.292 s | 2402.198 s | 13.804 s | 4.292 s |
| Output | 31.525 s | 31.525 s | 0.202 s | 31.525 s | 31.525 s | 0.202 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, T.; Wang, Y.; Chen, Y.; Jia, J.; Wen, M.; Guo, R.; Wu, T.; Deng, X. Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sens. 2021, 13, 2607. https://doi.org/10.3390/rs13132607
Xue T, Wang Y, Chen Y, Jia J, Wen M, Guo R, Wu T, Deng X. Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sensing. 2021; 13(13):2607. https://doi.org/10.3390/rs13132607
Chicago/Turabian StyleXue, Tianru, Yueming Wang, Yuwei Chen, Jianxin Jia, Maoxing Wen, Ran Guo, Tianxiao Wu, and Xuan Deng. 2021. "Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction" Remote Sensing 13, no. 13: 2607. https://doi.org/10.3390/rs13132607
APA StyleXue, T., Wang, Y., Chen, Y., Jia, J., Wen, M., Guo, R., Wu, T., & Deng, X. (2021). Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sensing, 13(13), 2607. https://doi.org/10.3390/rs13132607