1. 서 론
근래, 저탄소에너지개발에 대한 세계적 추세는 재생에너지 및 청정에너지에 의한 발전에 관심이 집중되고 있다. 이는 화석에너지의 확충에 따른 지구온난화와 환경오염 및 원자력발전에 대한 안전성 등의 문제에 대한 대안으로 연구 · 개발이 시작되었으며, 현재 지구온난화에 따른 환경변화를 적극적으로 대처하면서 탈원전을 정부시책으로 하는 유럽을 필두로 많은 국가에서 재생에너지 및 청정에너지에 대규모 투자를 실시하고 있다. 재생에너지 및 청정에너지 중에 파력발전은 기존 혹은 신규방파제나 호안에 관련시설을 설치하는 경우 청정도와 경제성이 높기 때문에 국내외적으로 실현장에 많이 계획 · 설치되고 있으며, 국내에서도 제주도에 그 사례(Ryu et al., 2007)를 볼 수 있다.
Falcão(2010)는 파력발전구조물(WEC; Wave Energy Converter)을 운동에너지의 변환방식에 따라 진동수주형, 가동물체형 및 월파형으로 분류하였다. 실해역에 파력발전구조물이 설치된 사례로 1985년에 노르웨이 해안에 건설되어 몇년 동안 가동된 월류형 파력발전구조물인 TAPCHAN(Tapered Channel Wave Power Device)을 들 수 있고, 1985년 노르웨이 Toftestallen(Bønke and Ambli, 1986), 1990년 일본 Sakata(Ohneda et al., 1991), 1990년 인도 Vizhinjam(Ravindran and Koola, 1991), 1999년 포르투갈 Pico(Falcão, 2000), 2000년 스코틀랜드 Islay(LIMPET; Land Installed Marine Power Transmitter; Heath et al., 2000)에 각각 건설된 진동수주형(OWC; Oscillating Water Column) 파력발전구조물을 들 수 있으며, 파랑에너지로부터 추출되는 전기동력은 60~500 kW의 범위에 있다. 여기서, 유용성이 가장 큰 것으로 알려진 진동수주형은 공기실 내부에서 파의 상하운동을 공기흐름으로 변환하여 공기터빈을 구동시키는 방식으로, 입사파랑의 주파수가 공기실의 고유주파수와 일치하게 되면 공진현상이 발생하게 되고, 결과적으로 공기실 내에 수면의 상하운동을 크게 증폭시킬 수 있으므로 에너지효율을 극대화시킬 수 있다(Cho, 2002).
이상의 진동수주형 파력발전구조물(OWC-WEC)에 있어서 파랑-구조물-내부공기의 상호간섭에 대한 연구를 해석적인 방법과 수치적인 방법으로, 그리고 입사파랑의 관점에서 분류하면 해석해로는 대표적으로 Evans and Porter(1997)의 연구를 들 수 있고, 수치해석에서는 대상파랑을 2차원규칙파랑(Evans and Porter, 1995; Greenhow and White, 1997; Malmo and Reitan, 1985; Kyoung et al., 2006; Nakamura and Nakahashi, 2005), 2차원불규칙파랑(Boccotti, 2007a, b; Gouaud et al., 2010; Falcão and Justino, 1999; Gervelas et al., 2011; Falcão and Rodrigues, 2002; Falcão, 2002; Yin et al., 2010), 3차원규칙파랑(EI Marjani et al., 2008; Josset and Clément, 2007; Paixão Conde and Gato, 2008; Cho, 2002), 그리고 3차원불규칙파랑(Delauré and Lewis, 2003)으로 각각 대별할 수가 있다. 수치해석기법으로 구분하면 고유함수전개법(Evans and Porter, 1995; Malmo and Reitan, 1985; Gouaud et al., 2010; Cho, 2002), 경계요소법(Josset and Clément, 2007; Delauré and Lewis, 2003), 유한요소법(Kyoung et al., 2006), Green 함수법(Nakamura and Nakahashi, 2005) 및 유한차분법(EI Marjani et al., 2008; Paixão Conde and Gato, 2008; Yin et al., 2010)이 있고, 여기서 다양한 수치기법이 적용되고 있는 것을 알 수 있다.
여기서, 공기실 내의 공기압의 변동은 공기실 내의 수면변동으로부터 발생되는 것으로 하여 공기압축성에 관한 상태방정식으로부터 변동공기압을 산정하는 것이 거의 대부분이다. 이로부터 Wells 터빈을 통과한 후의 공기압과의 차이로부터 Wells 터빈에 의한 전기에너지로의 변환효율을 검토한다. 실제로, 공기실 내의 공기흐름속도를 직접적으로 평가한 연구는 혼상류해석법에 의한 Lee et al.(2011, 2013b)과 Park(2013) 등이 있고, 간접적으로 평가한 연구는 CADMAS-SURF 모델(CDIT, 2001)과 3D-NIT 모델로부터 공기실 내에서 수위변동을 산정하여 공기흐름속도를 도출한 Lee et al.(2011, 2012, 2013a) 등이 있지만 이들을 제외하면 연구가 매우 미흡한 실정이다. 한편, RANS(Reynolds Averaged Navier-Stokes Solver) 및 k-ε 난류모델에 기초한 FLUENT code를 적용하여 유한차분법으로 해석하는 기법(EI Marjani et al., 2008; Paixão Conde and Gato, 2008; Yin et al., 2010)이 적용되고 있지만 3차원공기흐름을 충분히 재현하고 있지는 못하다.
본 연구에서는 단독으로 독립된 WEC를 설치하는 경우는 비경제적이라는 점을 고려하고, 또한 이형블록으로 피복된 기존 혹은 신규방파제에 WEC를 설치하는 경우 상대적으로 반사율이 증가되어 전면해역의 파랑환경이 악화될 수 있는 점 등을 감안하여 기존 OWC-WEC의 하부에 방파제의 전 · 후를 관통하는 해수소통구를 구비한 신형식의 OWC-WEC를 상정한다. 해수소통구는 방파제의 전면에서 고파랑에너지를 후면으로 소통시켜 방파제 전면에서 파고를 감소시킬 수 있고, 동시에 해수교환을 통해 항내 수질의 유지 · 개선을 도모할 수 있다. 이러한 해수교환기능을 고려한 경우로 Nakamura and Nakahashi(2005)와 Lee et al.(2013a)에 의한 연구를 대표사례로 들 수 있지만 Nakamura and Nakahashi(2005)의 경우는 공기실 내부에서 형성되는 와류를 이용한 발전을 고려하였고, Lee et al.(2013a)은 본 연구와 동일한 OWC-WEC를 고려하였다.
이상에서 기술한 해수소통기능을 겸비한 본 연구의 OWC-WEC에 대해 공기실 내에서 공기흐름, 해수소통구에서 해수흐름 및 구조물에 의한 반사율 등을 해석하기 위하여 3차원혼상류수치모델인 OLAFLOW(Higuera et al., 2018)를 이용하며, 대상의 파랑은 규칙파랑으로 한정한다. OLAFLOW(Higuera et al., 2018)는 RANS에 유한체적법을 적용하는 공개된 CFD code로, 불규칙파랑도 해석가능하다. 해석에서는 자유수면추적에 VOF 법(Kissling et al., 2010)을, 난류해석에 LES 모델(Smagorinsky, 1963)을 각각 적용하며, Multipaddle piston 방식의 조파기능과 Cutting-edge 기술로부터 감쇠영역을 구현한 3차원수치파동수조를 적용한다.
먼저, 본 연구의 OWC-WEC에 대해 공기실 내의 상단에 설치된 노즐에서 OLAFLOW에 의한 공기유출속도와 기존의 수치해석 및 수리모형실험으로부터 얻어진 값을 비교 · 검토하고, 또한 공기실 내에서 수면변동 등에 대해서도 기존의 수치해석과 수리실험에 의한 결과를 서로 비교 · 검토하여 OLAFLOW 모델의 타당성을 검증한다.
이상과 같은 OLAFLOW 모델의 적용성을 근거로, 해수소통구를 겸비한 OWC-WEC에 있어서 입사파고와 주기의 변화에 따른 공기실 내에서 수위변동, 상단 노즐에서 공기유출속도, 해수소통구 내에서 해수흐름 및 반사율 등의 변동특성을 면밀히 검토한다.
2. 수치해석이론
본 연구에서 이용한 3차원혼상류의 수치해석모델인 OLAFLOW(Higuera et al., 2018)는 비혼합 · 비압축성의 혼상유체(액체 및 기체)의 해석을 위하여 식(1)의 연속방정식과 식(2)의 RANS(Reynolds-Averaged Navier-Stokes) 방정식을 유한체적법에 기초하여 이산화한다.
여기서, t는 시간, xi는 공간벡터좌표, ρ는 유체의 밀도, ui(i = x, y, z)는 유체속도의 Cartesian 성분, p*는 Pseudodynamic 압력, Xj는 위치벡터, gi는 중력가속도를 각각 나타내며, μeff는 μ + νturb로 μ는 점성계수, νturb는 난류동점성계수이다.
액체와 기체의 경계면은 계산격자 내에서 유체가 점유하는 체적을 나타내는 VOF 함수 F를 이용하는 VOF 법을 적용하며, VOF 법에서는 액체셀의 경우 F = 1, 기체셀의 경우 F = 0, 그리고 액체와 기체를 모두 포함하고 있는 경계셀의 경우는 0 < F < 1의 값을 갖는다. VOF 함수 F는 식(3)의 이류방정식에 의해 계산된다.
여기서, uic는 인공압축항으로, |uic| =min[cα|ui|, max(|ui|)]과 같이 주어지며, 본 연구에서는 cα = 1을 적용하였다. 또한, 각각의 계산셀에서 유체의 밀도 ρ와 점성계수 μ는 VOF 함수를 가중치로 적용하여 다음과 같이 산정될 수 있다.
또한, 전술한 난류동점성계수 νturb는 LES 모델(Smagorinsky, 1963)을 적용하여 산정하였으며, 그 밖의 OLAFLOW(Higuera et al., 2018)에 대한 상세한 수치해석기법은 OLAFLOW의 매뉴얼 (https://github.com/phicau/olaFlow/tree/master/reference)을 참조하기 바란다.
3. 수치해석의 검증
3.1 OWC-WEC의 공기실 내에서 수위변동과 노즐에서 공기흐름속도
먼저, 본 절에서는 Fig. 1에 제시한 OWC-WEC의 공기실 내에서 수위변동 η와 상단 노즐에서 공기유출 · 입속도 V를 실험적으로 검토한 Iturrioz et al.(2015)의 결과와 3차원혼상류의 OLAFLOW 모델(Higuera et al., 2018)에 의한 수치해석결과를 비교 · 검토한다. Fig. 2는 Iturrioz et al.(2015)의 수리모형실험 Case C24(입사파고 H = 8 cm, 입사주기 T = 1.3 s)에서 수행된 실험결과와 OLAFLOW에 의한 수치결과를 비교한 것으로, Fig. 2(a)가 내부 공기실에서 수위변동을, Fig. 2(b)가 상단 노즐을 유 · 출입하는 공기흐름속도를 각각 나타낸 것이다. 먼저, 수위변동을 살펴보면 상대적으로 파봉에서 평탄하고, 파곡에서 뾰족한 비선형현상을 나타내고 있고, 수치해석결과가 실험치보다 약간 큰 값의 변동을 나타내지만 전반적으로 시간변동에 따른 실험치의 변화를 매우 합리적으로 재현하고 있는 것을 알 수 있다. 다음으로, 공기흐름속도의 경우 수위변동과는 달리 상대적으로 평탄한 파곡과 뾰족한 파봉으로 주어지는 비선형 현상에 대한 실험결과를 잘 구현하고 있고, 전술한 수위변동보다는 공기흐름속도의 경우가 시간변동에 따라 실험결과와 수치결과의 대응성이 우수하다는 것을 확인할 수 있다. 따라서, 이상과 같은 수위변동과 공기흐름속도에 관한 두 결과의 비교 · 검토로부터 본 수치연구의 타당성을 확인할 수 있다.
3.2 OWC-WEC의 공기실 전면과 내부에서 수위변동 및 노즐에서 최대공기흐름속도
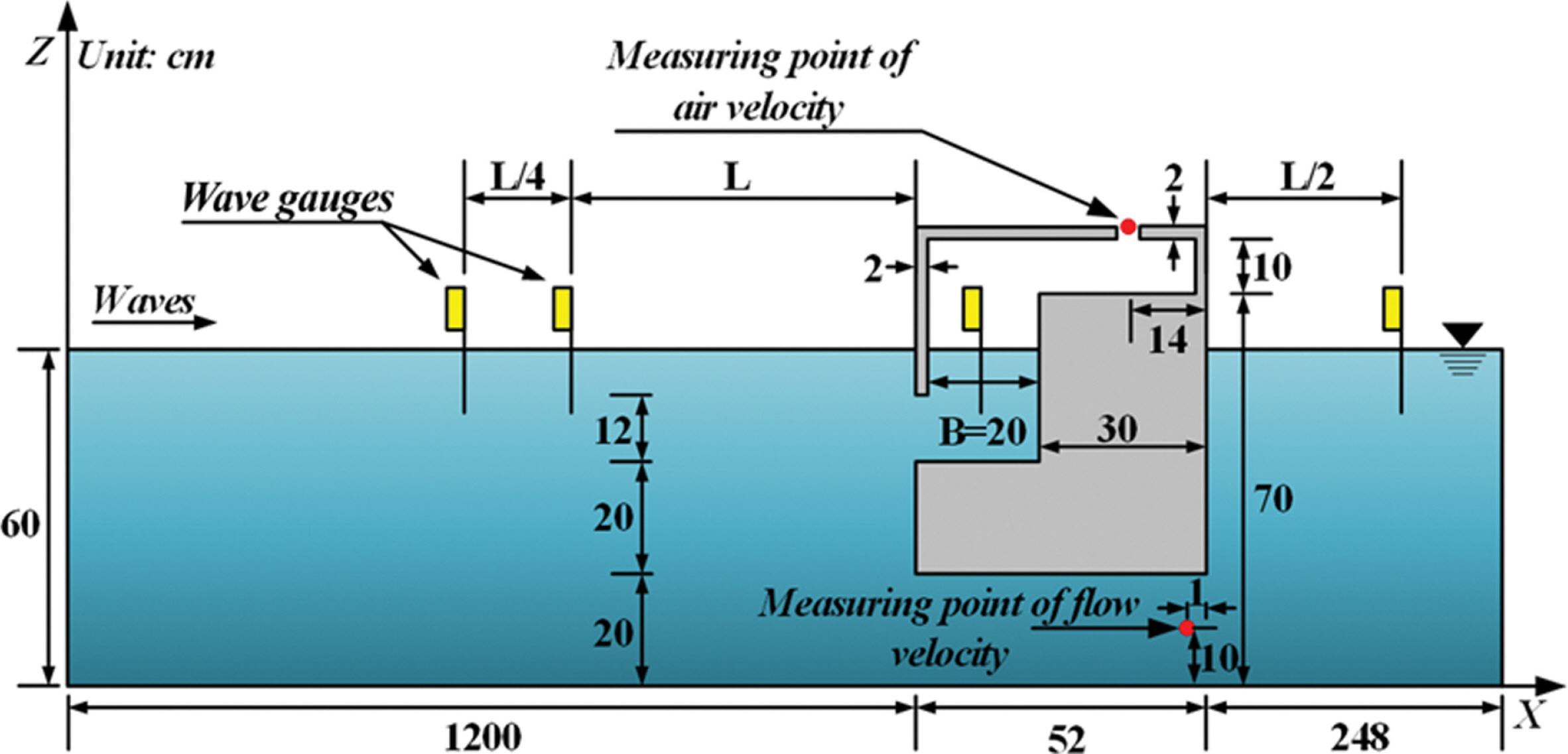
OLAFLOW 모델(Higuera et al., 2018)에 의한 3차원수치파동수조에서 OWC-WEC에 관한 수치해석결과의 타당성을 확인하기 위하여 Lee et al.(2012)에 의한 실험 및 수치결과와 비교한다. Lee et al.(2012)은 Fig. 3에 제시된 OWC-WEC에 대해 공기실 전면 및 내부에서 수위변동과 상단의 노즐에서 공기흐름속도를 실험으로부터 계측하였고, 또한 그들이 개발한 3D-NIT 모델을 적용하여 실험치를 재현하였으며, 특히 공기실 내에서의 수위변동으로부터 간접적인 방법을 사용하여 공기흐름속도를 산정하여 그의 특성을 평가하였다. 본 연구에서는 Fig. 3에 나타낸 바와 같이 Lee et al.(2012)과 동일한 구조물의 형상과 크기를 적용하고, 그리고 그들과 동일한 입사파랑조건을 사용하여 OLAFLOW 모델로부터 도출된 수치해석결과와 각각 비교한다.
Figs. 4와 5는 Lee et al.(2012)에 의한 실험결과와 3D-NIT 모델(Lee et al., 2012)에 의한 수치해석결과 및 본 연구에서 수행된 OLAFLOW(Higuera et al., 2018)에 의한 수치해석결과를 각각 비교한 것으로, Fig. 4가 Fig. 3에서 나타내는 바와 같이 공기실 전면에서 1 cm 이격된 지점에서 수위변동이고, Fig. 5가 공기실 내부의 중앙지점에서 수위변동을 각각 나타낸다. 그림에서 T는 입사파의 주기, H는 입사파고, B는 공기실의 폭, L은 입사파장을 각각 나타내며, 수심 h는 20 cm로 고정되었다.
먼저, Fig. 4를 살펴보면 Fig. 4(a)→(b)→(c)로 갈수록 파동에서 비선형성의 척도를 나타내는 Ursell수 Ur(= HL2/h3)을 산정하면 각각 Ur = 1.36, 7.74, 9.79로 산정되며, 따라서 비선형성분이 점차로 강하게 나타나는 것을 확인할 수 있다. Fig. 4(a)를 제외하면 전체적으로 파봉에서 본 수치해석결과가 실험치보다 약간 큰 값을 나타내지만 전체적으로 Ursell 수의 증가에 따른 상 · 하 및 좌 · 우에서 비대칭성의 발달과정이 실험결과와 잘 일치하는 것으로 판단된다. 그리고, 3D-NIT(Lee et al., 2012)에 의한 수치해석결과와 비교하면 실험결과를 거의 동일한 정도로 재현하는 것을 알 수 있지만 3D-NIT는 실험치보다 다소 작은 값을 나타내는 반면, OLAFLOW(Higuera et al., 2018)는 실험치보다 다소 큰 값을 각각 나타낸다.
다음으로, Fig. 5는 공기실 내부의 중앙에서 수위변동을 측정한 것으로, 그림에서 입사파랑조건은 Fig. 4의 각 경우와 동일하다. 그림으로부터 OLAFLOW(Higuera et al., 2018)에 의한 수치결과가 3D-NIT(Lee et al., 2012)에 의한 수치결과보다 실험치에 더 가까운 결과를 나타내며, 특히 Fig. 5(c)의 파곡부분에 이러한 경향이 강하게 나타난다는 것을 확인할 수 있다. 전체적으로는 전술한 Fig. 4의 공기실 전면에서보다 비선형성분이 약하게 나타나고, 파형에서 좌우대칭성이 상대적으로 강하게 나타난다는 것을 알 수 있다.
한편, 다음의 Fig. 6은 공기실 내부의 상단에 고정된 노즐에서 최대공기흐름속도 Vmax를 나타낸 결과이며, 그림에서는 혼상류해석모델인 TWOPM-3D(Park, 2013)에 의한 결과도 병기한다. 그림에서 TWOPM-3D와 OLAFLOW(Higuera et al., 2018)에 의한 두 결과는 혼상류해석모델이기 때문에 직접적으로 도출된 결과이고, 3D-NIT 모델(Lee et al., 2012)은 전술한 바와 같이 공기실 내부의 수위변동의 시간변화율에 연속방정식을 적용하여 공기흐름속도를 간접적으로 도출한 결과이다. 결과를 살펴보면 최대공기흐름속도는 공기실 폭이 고정되어 있기 때문에 파장이 길어질수록 실험 및 수치결과 모두 커지는 경향을 나타내며, 혼상류해석모델인 TWOPM-3D(Park, 2013)와 OLAFLOW(Higuera et al., 2018)에 의한 두 결과는 실험결과를 고정도로 재현할 수 있다는 것을 알 수 있다. 반면, 3D-NIT 모델(Lee et al., 2012)에 의한 수치결과는 실험치와는 다소 상이한 결과를 나타내고, 또한 TWOPM-3D와 OLAFLOW에 의한 두 결과보다 큰 결과를 나타낸다.
이상으로부터 공기실 내에서 수위변동과 공기흐름속도에 대한 기존의 수리실험결과와 수치해석결과 및 OLAFLOW(Higuera et al., 2018)에 의한 수치해석결과를 각각 비교 · 검토함으로서 본 논문의 OWC-WEC에 대해 산정되는 OLAFLOW에 의한 수치결과의 타당성을 충분히 검증하였다. 이하에서는 해수소통구를 구비한 신형식의 OWC-WEC를 대상으로 입사파랑조건의 여러 변화에 따른 반사율, 공기흐름속도 및 해수소통구에서 흐름속도 등을 해석하여 그의 특징을 면밀히 검토 · 논의한다.
4. 수치해석
4.1 수치해석 조건
본 연구에서는 제체하부에 해수소통구를 구비한 OWC-WEC에서 구조물에 의한 입사파의 반사율과 전달율, 노즐을 유 · 출입하는 공기흐름속도 및 해수소통구를 통한 해수의 유 · 출입속도의 특성을 규명하기 위하여 이하에서 OLAFLOW(Higuera et al., 2018)에 의한 3차원수치시뮬레이션을 수행하였다. 본 연구에서 적용한 3차원수치파동수조는 Fig. 7과 같이 길이 1,500 cm, 폭 54 cm, 높이 150 cm 및 60 cm의 일정수심으로 구성되며, 높이 20 cm의 해수소통구를 가진다. OWC-WEC는 폭 20 cm의 공기실을, 그 상단에 직경 4 cm의 노즐을 갖는다.
수위변동은 구조물 전면에 2점(구조물 전면에서 L과 5L/4 이격된 지점) 및 구조물 후면(구조물 배면에서 L/2 이격된 지점)에 1점에서 각각 측정되며, 공기흐름속도는 노즐 중심에서 외측인 좌표점(12.38 m, 0.27 m, 0.82 m)에서 측정된다. 또한, 해수소통구에서 흐름속도는 중앙위치인 좌표점(12.26 m, 0.27 m, 0.1 m)에서 측정되고, 평균유속은 중앙위치(x = 1,226 cm)에서 단면평균된 값이다.
Fig. 8은 OWC-WEC의 형상과 크기에 대한 상세도이다. 구조물의 두께는 2 cm의 평판으로 구성되어 있고, 해수소통구는 50 cm의 폭과 20 cm의 높이의 단면을 가진다. 파랑이 유입되는 상단부의 단면은 50 cm의 폭과 12 cm의 높이를 가지며, 내부 공기실은 너비 50 cm이다. 공기실에서 공기는 구조물의 상단에 위치하는 지름 4 cm의 노즐을 통해 유 · 출입된다. Fig. 9는 노즐에서 공기흐름속도와 해수소통구 내에서 유속의 측정위치와 좌표점을 각각 나타낸다.
Table 1은 본 수치해석에 적용한 규칙파랑의 제원과 Ursell 수 및 공기실 폭에 대한 조건을 나타낸다. 계산영역에서 격자크기는 수평방향으로 0~1,200 cm까지는 가변격자를 적용한 Δx = 6~2 cm, Δy = 2 cm, Δz = 2 cm로 각각 구성하고, 1,200~1,500 cm까지는 일정격자로 구성하였다. 구성된 격자에 대한 Courant 상수는 0.5 이하가 되도록 시간간격을 조정하면서 수치실험을 수행하였다. 경계조건으로는 계산영역의 모든 벽면에서 Neumann조건을 적용하였다.
4.2 반사율과 전달율
다음의 Fig. 10은 Table 1에 제시한 입사파랑조건을 모두 적용하여 OLAFLOW 모델(Higuera et al., 2018)로부터 산정된 구조물 주변에서의 수위변동으로부터 구조물에 의한 반사율 Kr과 전달율 Kt을 추정한 결과이다. 여기서, 반사율은 Goda and Suzuki(1976)의 2점법으로 얻어졌으며, 전달율은 구조물의 후면에 설치된 파고계로부터 전달에너지를 산정하고 이에 입사에너지를 나누어서 얻어졌다. 그림으로부터 반사율은 L/B≒ 9에서 최소값을 나타내고, 이를 중심으로 좌우의 L/B로 갈수록 증가하는 경향을 나타내지만 L/B > 11의 영역에서는 상대적으로 완만한 증가를 나타내므로 증가율이 그다지 크지 않다. 반면, 전달율의 경우는 L/B의 특정치에서 최소 혹은 최대를 나타내지 않고, L/B가 증가할수록, 즉 입사주기가 증가할수록 전반적으로 증가하는 경향을 보인다.
4.3 노즐에서의 공기흐름속도
4.3.1 공기흐름속도의 시계열
Fig. 9(a)에 나타낸 노즐에서 공기흐름속도를 3차원혼상류의 OLAFLOW 모델(Higuera et al., 2018)로부터 직접적으로 도출하여 그의 시계열을 나타낸 것이 다음의 Fig. 11이다. 그림에는 Table 1에 제시된 모든 입사파랑조건에 대해 제시하고 있다. 그림에서 (+)는 공기실 내에서 파봉이 형성되어 압축공기가 공기실 내부에서 외부로 유출되는 경우이고, (−)는 역으로 공기실 내에 파곡이 형성되어 외부의 비압축공기가 공기실 내부로 유입되는 경우에 해당한다. 전체적으로, CASE 01→CASE 02→…→CASE 13으로 전이될수록 Table 1에 나타낸 바와 같이 Ursell수가 커지는 상황이며, 이에 따른 공기흐름속도의 상 · 하진폭이 증폭되는 경향을 나타낸다. 이러한 결과는 전술한 Fig. 6에서의 경향과 일치한다. 한편, 공기유출속도의 상 · 하진폭을 살펴보면 (+)의 진폭이 (−)의 진폭보다 큰 값을 나타내는 것을 알 수 있고, 따라서 공기실 내부에서 외부로 유출되는 공기속도가 외부에서 공기실 내부로 유입되는 공기속도보다 더 크다는 것을 나타낸다.
다음의 Fig. 12는 Table 1의 CASE 10의 경우에 공기실 내부에서 수위변동과 상단에 놓인 적은 단면적의 노즐을 통하여 유 · 출입되는 공기흐름속도의 벡터를 시 · 공간적으로 나타낸 결과이다. 먼저, Fig. 12(a)는 공기실 내부에서 수위가 상승하는 단계에서 수위변동 및 공기흐름속도의 벡터를 나타낸 것으로, 그림으로부터 공기가 노즐에서 외부로 향하여 강한 흐름으로 유출되는 것을 시각적으로 볼 수 있다. 그리고, Fig. 12(b)는 공기실 내부에서 수위가 최고점 근방에 도달한 시각에서 수위변동 및 공기흐름속도의 벡터를 나타낸 것으로, 그림에서 공기가 노즐을 통하여 외부로 유출되는 것을 볼 수 있지만 전술한 Fig. 12(a)보다는 강도가 상대적으로 적다는 것을 알 수 있다. 여기서, 전술한 두 경우에 공기실 전면에서 수위변동과 공기실 내부에서 수위변동 사이에 큰 위상차가 발생한다는 것을 확인할 수 있다. 한편, Fig. 12(c)의 경우는 공기실 내부에서 수위가 하강하는 단계에서 수위변동 및 공기흐름속도의 벡터를 나타낸 것으로, 외부의 비압축공기가 노즐을 통하여 공기실 내부로 강하게 유입되는 것을 시각적으로 볼 수 있다. 반면, Fig. 12(d)는 공기실 내부에서 수위가 최저점 근방에 도달한 시각에서 수위변동 및 공기흐름속도의 벡터를 나타낸 것으로, 외부공기가 노즐을 통하여 내부로 약간 유입되지만 Fig. 12(c)보다는 강도가 많이 적으며, 공기실 내부의 공기가 와류를 형성한다는 것을 볼 수 있다.
이상으로부터 노즐을 통한 공기흐름은 공기실 내부의 수면변동과 직접적인 관계로 나타나며, 실제는 수면변동의 시간변화율(수면변동속도)의 함수로 주어진다(Lee et al., 2012). 따라서, 공기실 내부의 수위변동이 최고점과 최저점 근방에 도달한 Figs. 12(b)와 (d)에서 공기흐름속도가 상대적으로 적은 값을 나타내는 것은 수면의 시간변화율이 적기 때문이다.
4.3.2 최대공기흐름속도
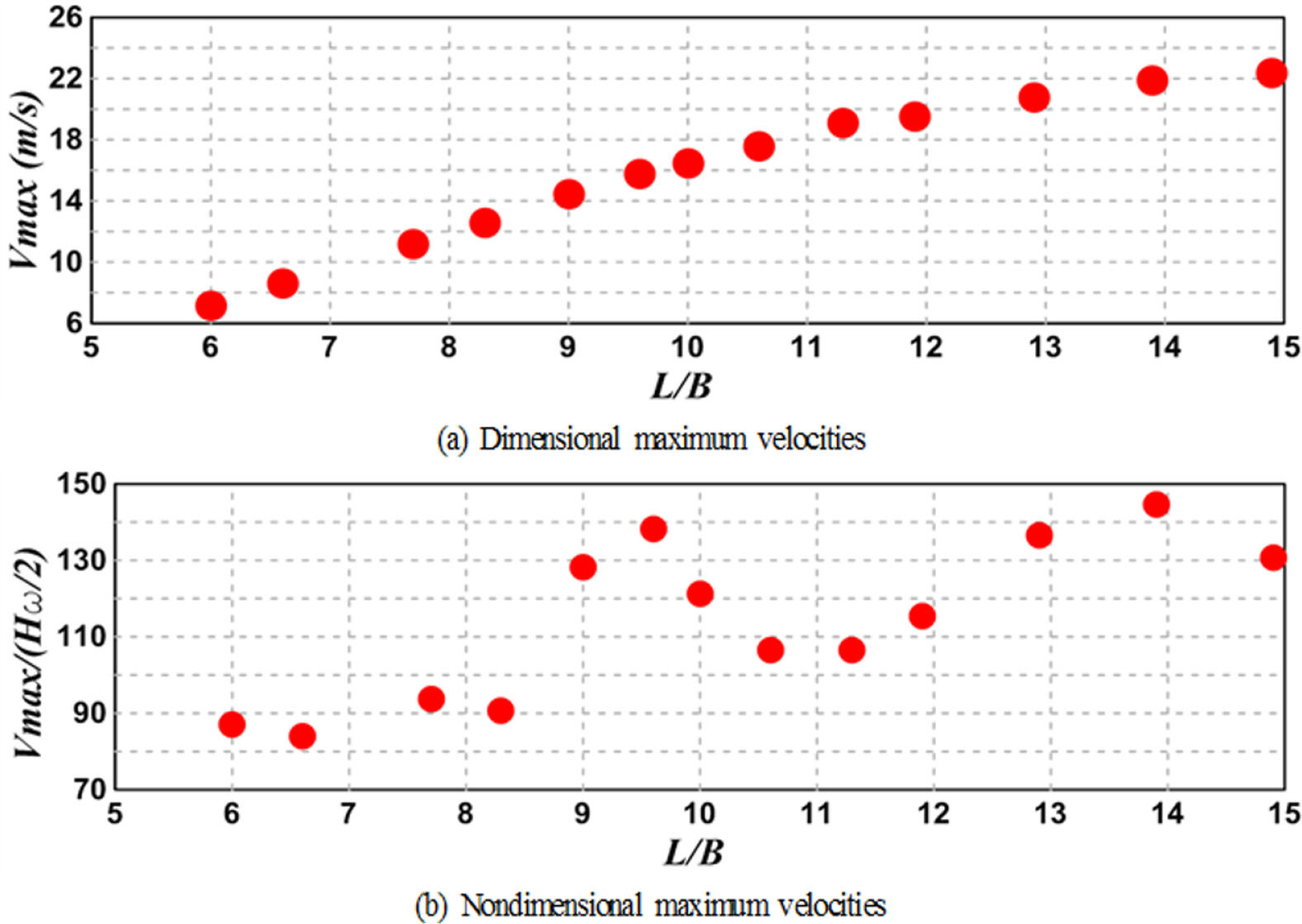
다음의 Fig. 13은 Fig. 11에서 나타낸 공기흐름속도의 시계열에서 최대치 Vmax만을 취해 도시한 것이며, Fig. 13(a)는 최대치의 실측치를 그대로 나타낸 것이고, Fig. 13(b)는 무차원값을 나타낸 것이며, 그림에서 ω(= 2π/T)는 각주파수를 나타낸다. Fig. 13(a)를 살펴보면 L/B가 증가함에 따라 노즐을 통한 최대공기흐름속도 Vmax가 증가하는 결과를 나타내며, L/B가 커질수록 최대공기흐름속도의 증가율은 상대적으로 완만해지는 경향을 나타낸다. 이러한 결과는 Fig. 11에 제시된 공기흐름속도에서 (+)진폭의 변화과정으로부터도 유추될 수 있다. 한편, Fig. 13(a)에서는 입사파고 H의 영향이 반영되지 않았으므로 Fig. 13(b)에서는 입사파고 H, 주기 T 및 수심 h의 영향을 모두 고려한 무차원최대공기흐름속도 Vmax/(Hω/2)와 L/B의 관계를 도시한다. 결과에 따르면 전술한 Fig. 13(a)의 경향과는 상이하게 무차원최대공기흐름속도 Vmax/(Hω/2)가 L/B≒ 9.7, 13.9에서 극대치를 나타내고, L/B≒ 11.0에서 극소치를 나타내는 것을 확인할 수 있다. 이러한 관계로부터 최대공기흐름속도는 입사파랑조건과 구조물의 크기에 각각 영향을 받는다는 것을 추정할 수 있고, 최대발전을 도모하기 위해서는 주어진 입사파랑조건에 적절한 크기의 구조물이 선정될 필요가 있다.
4.4 해수소통구에서의 평균유속
4.4.1 해수소통구에서에서 유속의 시계열
Fig. 9(b)에 나타낸 해수소통구의 중앙위치에서 흐름속도를 3차원혼상류의 OLAFLOW 모델(Higuera et al., 2018)로부터 직접적으로 도출하여, 그의 시계열을 나타낸 것이 다음의 Fig. 14이다. 그림에는 Table 1에 제시된 모든 입사파랑조건에 대한 각각의 결과를 제시하고 있다. 그림에서 (+)는 OWC-WEC의 전면에 파봉이 형성되어 항외측에서 항내측으로 유입되는 경우이고, (−)는 역으로 OWC-WEC의 전면에 파곡이 형성되어 항내측에서 항외측으로 유입되는 경우에 각각 해당한다. 전술한 바와 같이 CASE 01→CASE 02→…→CASE 13으로 전이될수록 Ursell수가 커지는 결과이며, 이에 따른 해수소통구 내 흐름속도의 상 · 하진폭이 크게 증폭되는 경향을 나타낸다. 이러한 결과는 전술한 Fig. 11에서 공기실 상단의 노즐에서 공기흐름속도의 경향과 일치하며, 이는 기본적으로 주기가 길어질수록, 그리고 입사파고가 클수록 수평방향의 물입자속도가 빨라지기 때문이다. 한편, 해수소통구 내부의 중앙위치에서 흐름속도의 상 · 하진폭을 살펴보면 (+)의 진폭이 (−)의 진폭보다 큰 값을 나타내는 것을 알 수 있고, 따라서 항외측에서 항내측으로 유입되는 흐름속도가 항내측에서 항외측으로 유입되는 흐름속도보다 더 크다는 것을 나타낸다. 이로부터 항내측에서 해수교환이 촉진되고, 항내수질이 유지 혹은 개선되는 효과가 발생한다.
4.4.2 해수소통구에서에서 평균유속
Fig. 15는 해수소통구 내 중앙위치에서 단면평균한 평균유속 U U
5. 결 론
본 연구에서는 Navier-Stokes solver에 기초한 유한체적법의 수치기법으로 3차원혼상류를 해석하는 공개된 CFD code인 OLAFLOW(Higuera et al., 2018)를 해수소통구를 구비한 진동수주형 파력발전장치(OWC-WEC)에 적용하여 일정수심의 규칙파 작용 하 구조물에 의한 반사율과 전달율, 노즐에서의 공기흐름속도 및 해수소통구 내에서 유속의 변동특성을 검토하였다. 이로부터 얻어지는 해의 타당성을 검증하기 위하여 기존의 실험결과 및 수치해석결과와 본 연구에 적용한 OLAFLOW(Higuera et al., 2018)의 수치해석결과와 서로 비교 · 검토하였다. 이러한 과정으로부터 3차원혼상류해석에 대한 OLAFLOW의 고정도를 충분히 확인할 수 있었다.
이상으로부터 규칙파동장에 설치된 해수소통구를 겸비한 OWC-WEC의 주변파동장에서 수위변동과 공기실 내에서 공기흐름속도 및 해수소통구에서 흐름속도의 추정에 OLAFLOW를 적용하여 수행된 본 연구의 범위 내에서 다음과 같은 중요한 사항을 알 수 있었다.
(1) 특정의 무차원공기실폭에서 최소반사율을 나타내고, 이를 중심으로 좌우의 무차원공기실폭으로 갈수록 반사율이 증가한다. 반면, 전달율은 입사주기가 증가할수록 전반적으로 증가한다.
(2) Ursell수가 커질수록 노즐에서 공기흐름속도가 증가하며, 공기실 내부에서 외부로 유출되는 공기속도가 외부에서 공기실 내부로 유입되는 공기속도보다 더 크다.
(3) 무차원최대공기흐름속도는 무차원공기실폭에 따라 극대치 혹은 극소치를 나타내며, 최대발전을 얻기 위해서는 주어진 입사파랑조건에 적절한 크기의 OWC-WEC가 선정될 필요가 있다.
(4) Ursell수가 커지면 해수소통구 내 흐름속도가 증가하며, 항외측에서 항내측으로 유입되는 흐름속도가 항내측에서 항외측으로 유입되는 흐름속도보다 더 크다.
(5) 해수소통구 내에서 평균흐름은 항외측에서 항내측으로 흐르며, Ursell수가 증가함에 따라 증가한다. 무차원평균유속은 특정한 무차원공기실폭에서 극대치와 극소치를 나타내지만 전체적으로는 주기가 길수록 증가하는 경향을 나타낸다. 따라서, 항내수질의 개선을 위해서는 주어진 입사파랑조건에 적절한 크기의 해수소통구가 선정될 필요가 있다.