Kraft

I fysikken er en kraft enhver interaksjon som forsøker å endre bevegelsen eller formen til et legeme, om det ikke er andre krefter som motvirker dette. Med andre ord kan en kraft føre til at et objekt med masse endrer sin hastighet, hvilket betyr at det endrer sin fart fra stillestående, eller fra én hastighet til en annen. En kraft kan også beskrives intuitivt som et skyv eller et drag. Krefter har både styrke og retning, noe som gjør at de betraktes som vektorer. I SI-systemet måles en kraft i Newton og blir ofte representert med symbolet $F$ eller, om det er snakk om en vektor, med $\mathbf {F}$ .

Newtons tre lover brukes for å analysere krefter og deres påvirkning. Den første loven sier at et legeme kun kan endre hastighet dersom det utsettes for en netto kraft. Den opprinnelige formen for Newtons andre lov sier at netto kraft som virker på en gjenstand er lik forandringen over tiden av bevegelsesmengden. Dersom massen til objektet er konstant, innebærer denne loven at akselerasjon av et legeme er direkte proporsjonal med nettokraft som virker på det, er i retning av denne nettokraften, og er omvendt proporsjonal med massen av objektet. Den tredje loven sier at når et legeme virker med en kraft på et annet legeme, vil det andre legemet også virke med en kraft på det første. Disse kreftene er like store og motsatt rettet. Dette innebærer at alle krefter er interaksjoner mellom ulike legemer, dermed finnes det ikke noe slikt som en ensrettet kraft eller en kraft som virker på bare et legeme.

Beslektede begreper til kraft er: skyvekraft, som øker hastigheten til et legeme, luftmotstand, som virker til å redusere hastigheten til et objekt, og dreiemoment som gir endring av rotasjonshastighet til et legeme. For et utvidet legeme vil hver del vanligvis virke med krefter på de tilstøtende parter; fordelingen av slike krefter gjennom legemet kalles for mekanisk spenning (eller stress). Trykk er en annen enkel form for spenning. Spenning fører vanligvis til deformasjon av faste materialer, eller strømninger i væskeer.

I moderne fysikk operere en bare med fire fundamentalkrefter: De sterke og svake kjernekrefter, den elektromagnetiske kraften som virker mellom elektriske ladninger, og gravitasjonskraft som virker mellom masser. Kjernekrefter virker bare på svært korte avstander, elektromagnetiske krefter virker på elektriske ladninger og tyngdekraften virker på alle masser i universet. Alle andre krefter er sammensatt av slike.

Den spesielle relativitetsteorien endret den moderne fysikks bilde av krefter, der blant annet betraktningen rundt krefter blir annerledes om hastighetene er svært store. Til tross for dette har Newtons bevegelseslover fremdeles stor relevans innenfor mekanikk, ettersom mange prosesser skjer ved relativt lave hastigheter.

Notasjon og måleenhet

I SI-systemet er enhet for kraft er newton, med symbol N. Denne størrelsen er definert som er den kraft som er nødvendig for å akselerere et legeme med én masse på ett kilo med en hastighet på én meter pr sekund i kvadrat, eller $kg\cdotm\cdots -2$ .^[1] Et mye brukt symbol for kraft er $F$ . Dersom kreftene representeres ved hjelp av vektorer, hvilket gir informasjon om retningen kreftene virker i, brukes fet skrift, $\mathbf {F}$ .

Historie

Filosofene i antikken

Aristoteles er berømt for sin beskrivelse av kraft som noe som fører et objekt til å gjennomgå «unaturlig bevegelse».

Foto: Eric Gaba

Filosofer i antikken, inkludert Aristoteles og Arkimedes, anvendte begrepet kraft i studiet av stasjonære og bevegelige gjenstander. Imidlertid hadde de grunnleggende feil i sin forståelsen av fenomenet. Delvis skyldes dette ufullstendig forståelse friksjon, som ikke alltid er en åpenbar kraft, og dermed utilstrekkelig syn på årsaken til naturlige bevegelser.^[2]

Siden antikken har begrepet kraft blitt anerkjent som en integrert funksjon av hvert av de såkalte enkle maskiner, som består av blant annet skråplanet, skruen, kilen vektstangen, hjulet med aksling og trinsen . Analyse av egenskapene til krefter kulminerte til slutt i arbeidet til Arkimedes. Spesielt er han kjent for sin behandling av oppdriftskraften som oppstår i væsker.^[2]

Aristoteles ga en filosofisk drøfting av begrepet om en kraft som en integrert del av sin aristoteliske kosmologi. I Aristoteles syn er den jordiske sfære bestående av fire elementer som kommer til hvile på forskjellige «naturlige steder» deri. Aristoteles mente at ubevegelige gjenstander på jorda hovedsakelig består av elementene jord og vann, og for å være i sin naturlige plass vil de være på bakken, hvor de vil holde seg hvis de blir overlatt alene. Han skilte mellom medfødt tendens til objekter til å finne sin «naturlige plass» (for eksempel for tunge legemer til å falle), noe som førte til «naturlig bevegelse», i motsetning til «unaturlig-» eller «tvungen bevegelse», som krevde kontinuerlig anvendelse av en kraft.^[3] Denne teorien var basert på den daglige opplevelsen av hvordan objektene beveger seg, som for eksempel den konstante anvendelsen av en kraft som er nødvendig for å holde en vogn i bevegelse. Men teorien hadde konseptuelle vanskeligheter med å forklare virkemåten til prosjektiler, for eksempel bevegelsen til en pil. Stedet hvor bueskytter setter prosjektilet i beveger var ved starten av banen, og mens prosjektilet seilte gjennom luften, kan det ikke observeres noen påvirkning som får den til å fare gjennom luften. Aristoteles var klar over dette problemet og foreslo at luften som fortrenges gjennom prosjektilets bane også bærer det til sitt mål. Denne forklaringen krever generelt at et kontinuum som luft er tilstede for enhver endring av plasseringen av et legeme.^[4]

Aristotelisk fysikk begynte å utsettes for kritikk i middelalderen, først med John Philoponus i på 600-tallet.^[5]

Galileo Galilei

Svakhetene ved aristotelisk fysikk ble ikke fullt ut korrigert før på 1600-tallet med arbeidet til Galileo Galilei, som var påvirket av den senere ideen fra middelalderen om at objekter i tvungen bevegelse bærer med seg en naturlig kraft, den såkalte impetus. Galilei konstruerte et eksperiment der steiner og kanonkuler begge ble satt til å rullet ned et skråplan for å motbevise Aristoteles teori om bevegelse tidlig på 1600-tallet. Han viste at legemer ble akselerert av tyngdekraften i en grad som var uavhengig av deres masse og hevdet at gjenstandene beholde sin hastighet hvis de ikke påvirkes av en kraft, for eksempel friksjon.^[6]

Galilei var også den første til å introdusere ideen om relative hastigheter.^[7] Fysikkens lover er de samme i hvert treghetssystem, det vil si i alle rammer som knyttes sammen av en galileitransformasjon. Nærmere bestemt vil det være slik at i systemer hvor legemer beveger seg med forskjellige hastigheter, er det umulig å bestemme hvilket legemer som er «i bevegelse», og hvilke som er «i ro». All bevegelse er relativ til annen bevegelse, og en gjenstand som er «i ro» har bare samme hastighet som andre gjenstander i samme treghetssystem.^[8]

Isaac Newton

En av de mest kjente anekdoter innenfor vitenskapshistorien er at et eple falt i Isaac Newtons hodet. Hendelsen ga ham briljant forståelse av tyngdekraftens natur, slik at lovene som er oppkalt etter ham omgående kunne nedtegnes. Det som imidlertid er bekreftet er at han snakket om at han fikk inspirasjon til sine arbeider om bevegelseslovene av å se fallende epler på sine eldre dager.^[9]

Foto: Klaus-Uwe Gerhardt

Isaac Newton beskrev bevegelse av alle objekter ved å bruke begrepene treghet og kraft, og dermed fant han at de følger visse bevaringslover. I 1687 publisere Newton sin avhandling Philosophiae Naturalis Principia Mathematica.^[10]^[11] I dette arbeidet formulerte Newton tre lover om bevegelse som fremdeles i dag er brukt for å beskrive krefter i fysikken.^[11]

Newtons første lov om bevegelse sier at legemer fortsetter å bevege seg i en tilstand av konstant hastighet med mindre de samlet sett blir påvirket av en kraft.^[11] Denne loven er en forlengelse av Galileis innsikt om at konstant hastighet var assosiert med en mangel på netto kraft. Newton foreslo at ethvert legeme med masse har en naturlig hviletilstand i den hastigheten det allerede har. Det vil si at Newtons empiriske første lov motsier den intuitive aristoteliske oppfatningen om at en netto kraft er nødvendig for å holde et objekt i bevegelse med konstant hastighet. Ved å gjøre «hvile» fysisk umulig å skille fra «ikke-null konstant hastighet», kobler Newtons første lov direkte treghet med begrepet relative hastigheter.

Newtons andre lov om bevegelse sier at kraften som påvirker et legeme er proporsjonalt med dets akselerasjon. I Principa Mathematica ble dette formulert som en endelig differanse basert på impuls.

Kraft og determinisme

Med hjelp av Newtons lover er det mulig å forutsi den tidsmessige utvikling av et fysisk system fra en gitt utgangssituasjonen og de virkende krefter. Dette gjelder ikke bare for enkelte eksperimenter i laboratoriet, men kanskje i prinsippet til universet som helhet? Denne konklusjonen bidro til oppfatningen av et deterministisk verdensbilde på 1700-tallet. Følgelig vil alle hendelser være fundamentalt forhåndsbestemte, selv om de beregninger som kreves for en forutsigelse er vanskelig i praktisk. Men i begynnelsen av 1900-tallet fant en ut at formler innenfor klassisk fysikk ikke var gyldige på atomnivå. Det deterministiske syn på verden som hadde blitt utledet fra formlene måtte derfor bli avvist i sin opprinnelige form.^[12]

Kraft i klassisk mekanikk

Newtons mekanikk

Utdypende artikkel: Newtons bevegelseslover

Første lov

Newtons første lov om bevegelse sier at legemer fortsetter å bevege seg i en tilstand av konstant hastighet med mindre de påvirket av en ytre netto kraft.^[11] Bevegelsen vil være rettlinjet, ikke for eksempel i en kurve, og gjelder relativt til annen bevegelse som skjer i samme treghetssystem. For eksempel vil det også være gyldig inni en bil eller et fly, dersom disse beveger seg med konstant hastighet.

Kraften vil regnes som en vektorsum, det vil si at dersom man for eksempel har tre krefter $\mathbf {F} _{1}$ , $\mathbf {F} _{2}$ og $\mathbf {F} _{2}$ vil det være den samlede kraften

\mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _{2}+\mathbf {F} _{3}

som gir netto kraft som virker på gjenstanden.

I praksis vil det alltid være krefter som virker på alle gjenstander til enhver tid. Likevel kan man tenke seg situasjoner der disse har veldig lite å si, som for eksempel en bevegelse i vakuum med neglisjerbar friksjon, slik at observerte endringer likevel er i tråd med denne loven.

Selv om Isaac Newton's mest berømte ligning er

\scriptstyle {\mathbf {F} =m\mathbf {a} }

, skrev han faktisk sin andre lov om bevegelse på en form som ikke bruker differensialregning.

Foto: Godfrey Kneller

Andre lov

Newtons andre lov kan skrives som

\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},

der $\mathbf {p}$ er bevegelsesmengden til systemet, og $\mathbf {F}$ er netto (vektorsum) av kraften. I likevekt er det per definisjon null netto kraft, men (balanserte) krefter kan uansett være til stede. I motsetning til dette fremgår det av andre lov at en ubalansert kraft som virker på en gjenstand vil resultere i at legemets bevegelsesmengde over tid endres.^[11]

Med definisjonen av bevegelsesmengde, kan uttrykket over skrives:

\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} \left(m\mathbf {v} \right)}{\mathrm {d} t}},

hvor m er masse og $\mathbf {v}$ er hastighet.^[13]^:9-1,9-2

Newtons andre lov gjelder bare for et system med konstant masse,^[a] og dermed kan m flyttes utenfor operatøren for den deriverte. Likningen blir da:

\mathbf {F} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}.

Ved å erstatte definisjonen av akselerasjon kan den algebraiske versjon av Newtons andre lov avledes:

\mathbf {F} =m\mathbf {a} .

Newton formulerte aldri eksplisitt formelen i sin redusert form som ovenfor.^[15] Med forhold der kraft og hastighet virker i samme retning kan formelen forenkles slik: ${F}=m\cdot {a}.$

Newtons andre lov sier at det er en direkte proporsjonalitet mellom akselerasjon og kraft, mens det er en invers forholdsmessigheten mellom akselerasjon og masse. Akselerasjoner kan defineres gjennom kinematiske målinger. Mens kinematikk er godt beskrevet gjennom referansesystemanalyse i avansert fysikk, er det fortsatt dype spørsmål som forblir ubesvart angående en riktige definisjon av masse. Generell relativitet gir en likeverdighet mellom romtid og masse, men mangler en sammenhengende teori om kvantegravitasjon. Det er uklart om hvordan, eller om, denne sammenhengen er relevant på mikronivå. Med en viss rett kan Newtons andre lov tas som en kvantitativ definisjon av masse ved å skrive loven som en likning, de relative enheter av kraft og masse er dermed faste.

Bruk av Newtons andre lov som en definisjon av kraft har blitt nedvurdert i noen av de mer strenge lærebøker,^[13]^:12-1^[16]^:59^[b] fordi det egentlig er en matematisk truisme. Kjente fysikere, filosofer og matematikere som har søkt en mer eksplisitt definisjon av begrepet kraft er Ernst Mach, Clifford Truesdell og Walter Noll.^[17]^[18]

Newtons andre lov kan anvendes for å måle styrken til krefter. For eksempel kan kunnskap om massene av planeter sammen med akselerasjonen til deres baner gjør det mulig for forskere å beregne tyngdekraften på planeter.

Tredje lov

Newtons tredje lov er blant annet vanlig å illustrere med to personer med skøyter som skyver hverandre. Hver av dem utveksler krefter, disse er motsatte og like store.

Newtons tredje lov er et resultat av å bruke symmetri på situasjoner der krefter kan tilskrives tilstedeværelse av ulike objekter. Den tredje loven innebærer at alle krefter er interaksjoner mellom ulike legemer,^[19]^[c] og dermed at det ikke finnes noe slikt som en ensrettet kraft eller en kraft som virker på bare et legeme. Når en først legemet utøver en kraft $\mathbf {F}$ på et annen legeme, vil det andre legemet utøver en kraft $-\mathbf {F}$ på det første legemet. $\mathbf {F}$ og $-\mathbf {F}$ er like i størrelse og motsatt i retning. Denne loven er noen ganger referert til som loven om reaksjon, med $\mathbf {F}$ kalt «aksjon» og $-\mathbf {F}$ «reaksjon». Aksjon og reaksjon skjer samtidig mellom to legemer kalt henholdsvis 1 og 2:

\mathbf {F} _{1,2}=-\mathbf {F} _{2,1}.

Hvis legeme 1 og legeme 2 anses å være i det samme systemet, så er netto kraften på systemet på grunn av samspillet mellom legemene 1 og 2 null siden

\mathbf {F} _{1,2}+\mathbf {F} _{\mathrm {2,1} }=0

\sum {\mathbf {F} }=0.

Dette betyr at i en lukket system av partikler, er det ingen indre krefter som er ubalansert. Det vil si at om aksjons-reaksjonskraften deles mellom hvilke som helst to legemer i et lukket system, ikke vil føre til at massesentrumet av systemet akselererer. Det er bestanddelene som bare akselerere i forhold til hverandre, selve systemet forblir uakselerert. Alternativt, hvis en ytre kraft virker på systemet, da vil senteret av massen oppleve en akselerasjon proporsjonal med størrelsen av den ytre kraft dividert med massen av systemet. Altså etter beskrivelsen som Newtons andre lov gir.^[13]^:19-1^[16]

Kombineres Newtons andre og tredje lov er det mulig å vise at lineær bevegelsesmengde til et system er bevart. Ved hjelp av

\mathbf {F} _{1,2}={\frac {\mathrm {d} \mathbf {p} _{1,2}}{\mathrm {d} t}}=-\mathbf {F} _{2,1}=-{\frac {\mathrm {d} \mathbf {p} _{2,1}}{\mathrm {d} t}}

og ved integrering med hensyn på tid, blir ligningen

\Delta {\mathbf {p} _{1,2}}=-\Delta {\mathbf {p} _{2,1}}

er oppnådd. For et system som omfatter legemene 1 og 2:

\sum {\Delta {\mathbf {p} }}=\Delta {\mathbf {p} _{1,2}}+\Delta {\mathbf {p} _{2,1}}=0

,

som er bevaring av lineær bevegelsesmengde.^[21] Brukes lignende argumenter er det mulig å generalisere dette til et system av et vilkårlig antall legemer. Dette viser at utveksling av fart mellom bestanddeler ikke vil påvirke netto bevegelsesmengde av et system. Generelt er det mulig å definere et system slik at netto bevegelsesmengde aldri går tapt eller vinnes, så lenge alle krefter skyldes interaksjonen av objekter med masse.^[13]^[16]

Beskrivelse av virkningen av krefter

Bruk av vektorer

Fritt-legeme-diagram (belastningsdiagram) av en kloss på et flatt underlag og et skråplan. Kreftene er dekomponert og lagt sammen for å bestemme deres størrelser og netto kraft.

Siden krefter blir oppfattet som skyv eller trekk kan dette gi en intuitiv forståelse for å beskrive krefter.^[10] Som med andre fysiske begreper (for eksempel temperatur), er den intuitive forståelse av kreftene kvantifisert ved hjelp av presise operasjonell definisjoner som er forenlig med direkte observasjoner og sammenlignet med en standardisert måleskala. Gjennom eksperimentering er det fastslått at laboratoriumsmålinger av krefter er i full overensstemmelse med den begrepsmessige definisjon av kraft som gis av newtonsk mekanikk.

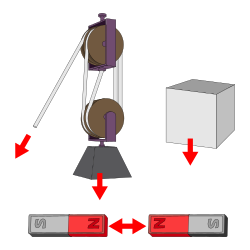
Krefter virker i en bestemt retning og har en størrelse avhengig av hvor sterk skyvet eller trekket er. På grunn av disse egenskapene er kreftene klassifisert som vektor størrelser. Dette betyr at krefter følger et annet sett av matematiske regler enn fysiske størrelser som ikke har retning (som kalles for skalare størrelser). For eksempel når det skal bestemmes hva som skjer når to krefter virker på samme legeme, er det nødvendig å kjenne både størrelsen og retningen av begge krefter for å beregne resultatet. Hvis begge disse opplysninger ikke er kjent for hver enkelt kraft, er situasjonen tvetydig. For eksempel hvis en vet at to personer drar på samme tau med kjente størrelser av kraften, men en ikke vet hvilken retning hver av personene trekker i, er det umulig å avgjøre hva akselerasjonen av tauet egentlig vil bli. De to personene kan trekke mot hverandre som i tautrekking, eller de to personene kan trekke i samme retning. I dette enkle endimensjonale eksemplet, er det umulig å bestemme hvorvidt nettokraft er et resultat av å legge sammen de to kraftstørrelsene eller trekke dem fra hverandre, uten å vite retningen av kreftene. Ved å knytte vektorer til krefter unngår en slike problemer. Illustrasjonen over til høyre viser et legeme som ligger på et bord med like store og motsatte krefter (øverst), mens legemet på skråplanet påvirkes av krefter slik at nettoresultatet gir bevegelse (nederst).

Historisk sett ble krefter først undersøkt kvantitativt i betingelser med statisk likevekt hvor flere kreftene kansellert hverandre. Slike eksperimenter demonstrerer viktige egenskaper som at krefter er vektorstørrelser, altså at de har størrelse og retning.^[10] Når to kreftene virker på en punktpartikkel er den resulterende kraft, altså resulterende (nettokraft), noe som kan bestemmes ved å følge parallellogramloven om vektoraddisjon: Summering av to vektorer som representert sidene i et parallellogram gir en tilsvarende resulterende vektor som er lik i størrelse og retning til den tverrgående linjen i parallellogrammet.^[13]^[16] Størrelsen av den resulterende kraften varierer fra differansen mellom de to størrelsene av de to kreftene, til sum av dem, alt avhengig av vinkelen mellom dem. Hvis imidlertid forskjellige krefter virker på et utvidet legeme, må deres respektive angrepspunktet på legemet hensynstas for å kunne bestemme virkningen for bevegelsen av legemet.

Fritt-legeme-diagram (belastningsdiagram) kan brukes som en praktisk måte å holde styr på krefter som virker på et system. Ideelt sett er disse diagrammene tegnet med vinkler og relative størrelsene av snittkrefter slik at grafisk summering av vektorer kan utføres. Kan gjøres for å bestemme netto kraft.^[22]

I tillegg til summering, kan krefter også dekomponeres i uavhengige komponenter som da står vinkelrett på hverandre. For eksempel kan en horisontal kraft som peker nordøst derfor deles opp i to krefter, en som peker mot nord og en som peker øst. Summeres disse komponentstyrkene med hjelp av vektoraddisjon fås den opprinnelige kraften. Illustrasjonen til høyre viser eksempel på dekomponering av tyngdekraften som virker på et legeme på et skråplan (nederst). Dekomponering av snittkrefter i komponenter av et sett med basisvektorer er ofte en bedre matematisk måte å beskrive krefter enn å bruke størrelser og retning.^[23] Årsaken er at for ortogonale komponenter blir komponentene til vektorsummen entydig bestemt av skalaraddisjonen av komponentene i de individuelle vektorene. Ortogonale komponenter er uavhengige av hverandre fordi krefter som virker vinkelrett på hverandre ikke har noen virkning på størrelsen eller retningen av den andre. Når valg av et sett av ortogonale basisvektorer gjøres, tas valget på grunnlag av en vurdering av hvilket sett av basisvektorer som være gjøre matematikken mest praktisk. Å velge en basisvektor som er i den samme retning som en av kreftene er ønskelig, ettersom kraften da vil ha bare en komponent forskjellig fra null. Ortogonale kraftvektorer kan være tredimensjonale med den tredje komponent i rett vinkel på de to andre.^[13]^[16]

Statisk likevekt

Likevekt inntreffer når den resulterende kraft som virker på en punkt partikkel er null (det vil si at er vektorsummen av alle krefter er null). Ved behandling av et utvidet legeme er det også nødvendig at nettomomentet i det er null. Generelt finnes det to typer likevekt, statisk- og dynamisk likevekt.

Statisk likevekt ble forstått godt før utviklingen av klassisk mekanikk. Objekter som er i ro har null netto kraft som virker på dem.^[24]

Det enkleste tilfelle av statisk likevekt oppstår når to krefter er like i størrelse, men har motsatte retninger. For eksempel er en gjenstand på et plant underlag trukket nedover mot sentrum av jorden på grunn av tyngdekraften. På samme tid vil overflatekrefter motstå den nedadrettede kraften med lik oppadrettet kraft (kalt normalkraften). Situasjonen gir null netto kraft og ingen akselerasjon. Press mot et objekt på en friksjonsflate, for eksempel et skråstilt bord, kan resultere i en situasjon hvor legemet ikke beveger seg, fordi den påførte kraft motvirkes av statisk friksjon, som oppstår mellom objektet og bordflaten. For en situasjon uten bevegelse vil den statiske friksjonskraft eksakt balansere den påførte kraften, noe som ikke gir akselerasjon. Den statiske friksjon øker eller minker i respons til den påførte kraften opp til en øvre grense. Denne øvre grensen er bestemt av egenskapene til kontaktflaten mellom bordflaten og legemet.^[10] Illustrasjonen over viser begge disse tilfellene, der kreftene er påført som vektorer (piler).

En statisk likevekt mellom to krefter er den mest vanlige måten å måle krefter på, og kan skje ved hjelp av enkle instrumenter som en vekt. For eksempel vil et legeme opphengt i en vertikal fjærvekt oppleve tyngdekraften som virker på den, balansert mot en kraft som utøves av fjærreaksjonskraften. Denne kraften tilsvarer objektets vekt. Ved hjelp av slike verktøy ble noen kvantitative lover om kraft oppdaget: at tyngdekraften er proporsjonal med volumet for legemer med konstant tetthet (allment utnyttet i årtusener for å definere standardvekter), Arkimedes' prinsipp for oppdrift, Arkimedes' analyse av Vektstang, Boyle-Mariottes lov for gasstrykk, og Hookes lov for fjærer. Disse ble alle formulert og eksperimentelt verifisert før Isaac Newton forklarte sine tre bevegelseslover.^[10]^[13]^[16]

Dynamisk likevekt

Galileo Galilei var den første til å peke ut de iboende motsetningene som finnes i Aristoteles' beskrivelse av krefter.

Foto: Justus Sustermans

Dynamisk likevekt ble først beskrevet av Galilei som la merke til at visse forutsetninger i den aristoteliske fysikken ble motsagt av observasjoner og logikk. Galilei innså at enkel hastighets addering krever et begrepet om «absolutt ro», noe som ikke kan eksisterer. Han konkluderte med at bevegelse i en konstant hastighet ble helt ekvivalent med ro. Dette var i strid med Aristoteles begrep om en «naturlig tilstand» av ro, og at legemer med masse tilstreber seg denne. Enkle eksperimenter viste at Galileis forståelse av likeverdighet mellom konstant hastighet og ro var riktige. For eksempel om en sjømann slipper en kanonkule fra utkikstønnen på et skip som beveger seg med en konstant hastighet, ville aristotelisk fysikk hevde at kulen faller rett ned mens skipet flytter seg under den fallende kulen. Konsekvensen blir at i et aristotelisk univers vil den fallende kanonkulen lande et stykke bak foten av masten til et skip i bevegelse. Men når dette eksperimentet faktisk blir gjennomført vil kanonkulen alltid falle rett ned ved foten av masten, som om kanonkulen «vet» at den reise med et skip, til tross for å være atskilt fra skipet under fallet. Siden det ikke er noen horisontal kraft som påføres i fremoverretning på kanonkulen når den faller, er den eneste konklusjon som er igjen at den fortsetter å bevege seg med samme hastighet som båten som før den faller. Dermed er det heller ingen kraft som kreves for å holde kanonkulen i bevegelse i konstant hastighet fremover.^[6]

Videre må et hvilken som helst legeme som beveger seg med en konstant hastighet være gjenstand for null nettokraft (resulterende kraft). Dette er definisjonen av dynamisk likevekt: når alle kreftene på et legeme balanseres vil det fortsatt bevege seg med konstant hastighet.

Et enkelt tilfelle av dynamisk likevekt oppstår under bevegelse av et legeme med konstant hastighet over en flate med kinetisk friksjon. I en slik situasjon påføres en kraft i bevegelsesretningen, mens den kinetiske friksjonskraften nøyaktig motsetter seg den påførte kraften. Dette resulterer i null netto kraft, men ettersom legemet startet med en hastighet forskjellig fra null, vil det fortsette å bevege seg. Aristoteles feiltolket denne bevegelsen som noe som er forårsaket av den påførte kraften. Men når kinetisk friksjon er tatt i betraktning er det klart at det ikke er noen netto kraft som forårsaker bevegelse med konstant hastighet.^[13]^[16]

Ikke-grunnleggende krefter

Normalkraften

F_N representerer normalkraften som utøves på et legeme og virker i normalt på det.

Når en bok ligger på et bord virker tyngdekraften på boken, altså ned mot jordens senter. Normalkraften er den som virker fra bordet mot boken, den er like stor og i motsatt retning av tyngdekraften som boken utsettes for. Om en plate har helning virker normalkraften fremdeles rett opp mot legemet, slik som figuren til høyre viser.

Normalkraften er også den kraften som virker når en ytre kraft skyver på et fast legeme. Et eksempel på normalkraften i aksjon er støtkraften på en gjenstand som krasjer i et ubevegelig underlag.^[13]^[16] Normalkraften er en konsekvens av de grunnleggende kreftene. Idealisert modeller anvendes for å gi fysisk innsikt, slik som den enkle figuren til høyre. Normalkraften virker på grunn av frastøtende krefter fra interaksjonen mellom atomer i nær kontakt. Når deres elektronskyer overlapper hverandre vil paulifrastøting (på grunn av fermionisk natur til elektroner) følge som resultat av den kraften som virker i rett vinkel på overflaten i grensesnittet mellom to objekter.^[25]^:93

Friksjon

Utdypende artikkel: Friksjon

Friksjon er en overflatekraft som motsetter seg relative bevegelser. Friksjonskraften er direkte relatert til normalkraften som virker for å holde to faste legemer adskilt ved kontaktpunktet. Det er to brede klassifiseringer av friksjonskrefter, nemlig statisk- og kinetisk (eller dynamisk, eller glidende) friksjon.

Den statiske friksjonskraften ( $\mathbf {F} _{\mathrm {sf} }$ ) vil nøyaktig motvirke de krefter som brukes på et legeme parallelt med en overflatekontakt opp til grensen som er angitt av koeffisienten for glide friksjon ( $\mu _{\mathrm {sf} }$ ) multiplisert med normalkraften ( $\mathbf {F} _{N}$ ). Med andre ord vil størrelsen av den kinetiske friksjonskraften tilfredsstille ulikheten:

0\leq \mathbf {F} _{\mathrm {sf} }\leq \mu _{\mathrm {sf} }\mathbf {F} _{\mathrm {N} }.

For forskjellige materialer som er i kontakt må forskjellige koeffisienter ( $\mu _{\mathrm {sf} }$ ) benyttes, disse finnes i egne tekniske tabeller.

Den kinetiske friksjonskraften ( $\mathbf {F} _{\mathrm {kf} }$ ) er uavhengig av både de krefter som virker og legemets bevegelse. Således vil størrelsen av den kinetiske friksjonskraften være:

\mathbf {F} _{\mathrm {kf} }=\mu _{\mathrm {kf} }\mathbf {F} _{\mathrm {N} },

der $\mu _{\mathrm {kf} }$ er koeffisienten for kinetisk friksjon. For de fleste overflategrenseflater, er koeffisienten til rullefriksjon mindre enn koeffisienten for kinetisk friksjon.

Strekk

Under en dragkamp virker det krefter på et tau som kalles strekkrefter. I den høyre delen av illustrasjonen er det vist et segment av tauet der aksjon-reaksjonspar av strekkreftene T er markert. Disse kreftene virker alltid aksialt. Hvert segment av tauet trekkes fra hverandre ved de to nabosegmentene, hvilket gir spenninger i materialet.

Mekanisk strekk er den trekkraften $\mathbf {T}$ som overføres aksialt ved hjelp av en streng, kabel, kjetting, eller lignende endimensjonal sammenhengende objekt, eller ved hver ende av en stang, fagverksbjelkeelement, eller tilsvarende tre-dimensjonale objekt. Strekk kan også beskrives som aksjon-reaksjonspar av krefter som virker i hver ende av slike sammenhengende elementer. Det motsatte av strekk er komprimering.

Bildet til høyre viser en dragkamp, og en del av tauet som er illustrert som et element viser aksjon-reaksjonspar kreftene som virker på det. Strekket vil endres langs lengden av et tauet, etter som det blir stadig færre som drar i tauet desto lengre ut mot tapene en kommer.

Et relatert begrep er mekanisk spenning som blir definert som kraft per arealenhet. Generelt blir formelen for spenning uttrykt ved:

\ {\sigma }={\frac {F}{A}}\,

Hvor $\ {\sigma }$ er spenning, ofte kalt normalspenning, $\ F$ er kraften som virker normalt på flaten med areal $\ A$ .

Dette begrepet brukes også i kontinuumsmekanikk, der en fullstendig beskrivelse skjer med en spennings-tensor. Denne formalismen inkluderer trykkbegrepet knyttet til kreftene som virker normalt på tverrsnittsareal (matrisediagonaler til tensoren) samt skjærkraftbegrepet knyttet til kreftene som virker parallelt til tverrsnittsarealet. Spenningstensoren står for krefter som forårsaker deformasjoner inkluderer strekkspenning og kompresjoner.^[10]^[16]^:133–134^[26]^{:38-1–38-11}

Elastisk kraft

F_k er kraften som reagerer på belastningen fra loddet i fjæren.

En elastisk kraft virker til å returnere en fjær til sin opprinnelige lengde. En ideell fjær vil være masseløst, friksjonsfri, uknuselig, og uendelig elastisk. Slike fjærer utøver krefter som presser når de sammenpresses, eller drar når de utvides, dette skjer i forhold til graden av forskyvning av fjæren fra sin likevektsposisjon.^[27] Denne lineær sammenhengen ble beskrevet av Robert Hooke i 1676, som Hookes lov er oppkalt etter. Hvis $\Delta x$ er forskyvningen så er kraften som utøves av en enkelt fjær er lik:

\mathbf {F_{k}} =-k\Delta \mathbf {x}

hvor $k$ er fjærkonstanten som er gitt av selve fjæren. Minustegnet står for tendensen kraften $\mathbf {F} _{k}$ har til å virke i opposisjon til den påførte belastningen.^[13]^[16] Se illustrasjon der påført belastning er mg, altså tyngden til loddet.

Kontinuumsmekanikk

Når dragkraften (

F_{d}

) forbundet med luftmotstanden blir lik i størrelse med tyngdekraften på et fallende legeme (

F_{g}

), har objektet en tilstand kalt dynamisk likevekt ved terminalfart.

Newtons lover og mekanikk generelt ble først utviklet for å beskrive hvordan krefter påvirker idealiserte punktpartikler heller enn for tredimensjonale objekter. Imidlertid vil materie ha en utvidet struktur i den virkelige verden, og krefter som virker på en del av et legeme kan påvirke andre deler av det. For situasjoner hvor gitterstrukturer som holder sammen atomene i et materiale som er i stand til å flyte, komprimeres, ekspandere, eller på annen måte endre form, er det utviklet teorier innenfor kontinuumsmekanikk som beskrive hvordan krefter påvirker materialet. For eksempel i utvidede væsker vil forskjeller i trykk resulere i krefter som er rettet langs trykk gradienter som følger:

{\frac {\mathbf {F} }{V}}=-\mathbf {\nabla } P

der $V$ er volumet til legemet i væsken, $\mathbf {\nabla }$ er Nabla-operatoren og $P$ er en skalar funksjon som beskriver trykket på alle steder i rommet. Trykkgradienter og differensialer resultere i oppdriftskraften for legemer som senkes ned i væsker i et gravitasjonsfelt, vind i atmosfæren, og løft knyttet til aerodynamikk og fly.^[13]^[16]

Et spesifikt eksempel på en slik kraft som er knyttet til det dynamiske trykket er væskemotstand, som er en kraft som virker på et legeme som beveger seg gjennom et fluid på grunn av viskositeten. Denne strømningsmotstand er en kraft som er tilnærmet proporsjonal med hastigheten, men motsatt i retning:

\mathbf {F} _{\mathrm {d} }=-b\mathbf {v} \,

hvor $b$ er en konstant som er avhengig av egenskapene til fluidet og dimensjonene av den gjenstand (vanligvis dets tverrsnittsareal), og $\mathbf {v}$ som er hastigheten til legemet.^[13]^[16] Se illustrasjon.

Trykk

Når en kraft påføres på en overflate er trykket som oppstår $p$ , gitt av størrelsen av vektoren som representerer denne kraften $\mathbf {F} _{\perp }$ vinkelrett på overflaten dividert på arealvektoren $\mathbf {A}$ :

p={\frac {|\mathbf {F} _{\perp }|}{\mathbf {A} }}

Legg merke til at trykk er en skalar enhet. Trykket er en såkalt intensiv tilstandsstørrele som brukes til å beskrive termodynamiske systemer. Andre slike tilstandsstørrelser er temperatur og entalpi.

Fiktive krefter

Det er krefter som er avhengig av referansesystem, noe som betyr at de oppleves på grunn av innføringen av et ikke-newtonsk referansesystem (det vil si referanseramme uten treghet). Slike krefter inkludere sentrifugalkraften og corioliskraften.^[28] Disse kreftene blir betraktet som fiktiv fordi de ikke finnes i referanserammer som ikke akselererer.^[13]^[16] Fordi disse kreftene ikke er ekte er de også referert til som «pseudo krefter».^[13]^:12-11

I generelle relativitet er gravitasjon en fiktiv kraft som oppstår i situasjoner der romtid avviker fra flategeometri. Som en forlengelse, Kaluza–Klein-teorien og strengteori tilskrives elektromagnetisme og andre fundamentale krefter, henholdsvis til krumningen av ulikt skalert dimensjoner, noe som til slutt ville innebære at alle krefter er fiktive.

Energibetraktninger

Kinematisk integraler

Hester som pløyer utfører arbeid. Arbeidet er proporsjornalt med kraftkomponenten i horisontal retning og tilbakelagt strekning, mens effekten er produktet av denne kraftkomponenten og hastigheten.

Foto: Ralf Roletschek/fahrradmonteur.de

Krefter kan anvendes for å definere en rekke fysiske konsepter ved integrering med hensyn på kinematiske variabler. For eksempel vil integrering av en kraft med hensyn på tid gi definisjonen av impuls:^[29]

\mathbf {I} =\int _{t_{1}}^{t_{2}}{\mathbf {F} \mathrm {d} t},

som ved bruk av Newtons andre lov vil tilsvare endringen i fart (som gir impuls).

Tilsvarende vil integrering med hensyn til posisjon gi en definisjon av utført arbeid av en kraft:^[13]^:13-3

W=\int _{\mathbf {x} _{1}}^{\mathbf {x} _{2}}{\mathbf {F} \cdot {\mathrm {d} \mathbf {x} }},

noe som tilsvarer forandringer av kinetisk energi (som gir arbeidet-energiteoremet).^[13]^:13-3

Effekt P er endringstakten dW/dt av arbeidet W etter som banen som et legeme blir forlenget beskrives med en posisjonsendring ${d}\mathbf {x}$ i et tidsintervall dt:^[13]^:13-2

{\text{d}}W\,=\,{\frac {{\text{d}}W}{{\text{d}}\mathbf {x} }}\,\cdot \,{\text{d}}\mathbf {x} \,=\,\mathbf {F} \,\cdot \,{\text{d}}\mathbf {x} ,\qquad {\text{ slik at }}\quad P\,=\,{\frac {{\text{d}}W}{{\text{d}}t}}\,=\,{\frac {{\text{d}}W}{{\text{d}}\mathbf {x} }}\,\cdot \,{\frac {{\text{d}}\mathbf {x} }{{\text{d}}t}}\,=\,\mathbf {F} \,\cdot \,\mathbf {v} ,

der ${\mathbf {v} {\text{ }}={\text{ d}}\mathbf {x} /{\text{d}}t}$ er hastigheten.

Om kraften og hastigheten er konstante kan uttrykket for arbeid forenkles til $W=F\,x$ og likeledes kan uttrykket for effekt $P=F\,v$ . I tilfeller der kraften ikke virker vinkelrett på legemet som flyttes kan følgende sammenheng benyttes for arbeid $W=F\,x\,\cos \alpha$ og for effekt $P=F\,v\,\cos \alpha$ der $\alpha$ er vinkelen mellom kraften og bevegelsesretningen.

Potensiell energi

Hooverdammen demmer opp Coloradoelven i USA. Den kunstige innsjøen heter Lake Mead, og inneholder en enorm mengde potensiell energi i form av vann i jordens tyngdefelt som kan omgjøres til elektrisk energi.

Utdypende artikkel: Potensiell energi

I stedet for kraft kan ofte det matematisk relatert konseptet med potensiell energi noen ganger brukes for enkelhets skyld. For eksempel kan gravitasjonskraften som virker på et legeme betraktes som virkningen av gravitasjonsfeltet som er til stede der legemet befinner seg. Omarbeides den matematisk definisjonen av energi (via definisjonen av arbeid), er et skalarfelt ${U(\mathbf {r} )}$ er definert som det feltet som har en gradient lik og motsatt av den kraften som produseres på hvert punkt:

\mathbf {F} =-{\boldsymbol {\nabla }}U.

Krefter kan klassifiseres som konservativt eller ikke-konservativt. Konservative krefter er lik gradienten til et potensial, mens ikke-konservative krefter ikke er det.^[13]^[16]

Konservative krefter

En konservativ kraft som virker på et lukket system har et tilhørende mekanisk arbeid som muliggjør at energi bare kan konverteres som kinetisk eller potensielle former. Dette betyr at for et lukket system er netto mekanisk energi konservert når en konservativ kraft virker på systemet. Denne kraften er derfor knyttet direkte til forskjellen i potensiell energi mellom to forskjellige steder i rommet,^[30] og kan anses å være en egenskap ved potensialfeltet på samme måte at retningen og mengden av en vannstrøm kan anses for å være en egenskap for et kotekart som beskriver landhevingen for et område.^[13]^[16]

Konservative krefter er gravitasjon, elektromagnetisk kraft, og fjærkraft. Hver av disse kreftene betraktes med modeller som er avhengig av en posisjon som ofte gitt som en radial vektor $\mathbf {r}$ som kommer fra sfærisk symmetriske potensialer.^[31] Noen eksempler på dette er:

For tyngdekraft:

\mathbf {F} =-{\frac {Gm_{1}m_{2}\mathbf {r} }{r^{3}}}

der $G$ er gravitasjonskonstanten, og $m_{n}$ er massen av legemet n.

For elektrostatiske krefter:

\mathbf {F} ={\frac {q_{1}q_{2}\mathbf {r} }{4\pi \epsilon _{0}r^{3}}}

der $\epsilon _{0}$ er den elektriske primitiviteten for vakuum, og $q_{n}$ er elektrisk ladning for legemet n .

For fjærkrefter:

\mathbf {F} =-k\mathbf {r}

der $k$ er fjærkonstanten.^[13]^[16]

Ikke-konservativ krefter

For visse fysiske systemer er det mulig å modellere krefter som har sitt opphav fra gradienter i potensialer. Dette skyldes ofte makroskopiske betraktninger som anser krefter å oppstå fra en makroskopisk statistisk gjennomsnittsbetraktning innenfor mikrotilstander. For eksempel er friksjon forårsaket av gradientene for mange elektrostatiske potensialer mellom atomer, men manifesterer seg som en kraft som er uavhengig av enhver makroposisjonsvektor. Andre ikke-konservative krefter, utenom friksjonen, er kontaktkraft, spenning, kompresjon og drag. Imidlertid vil en med en tilstrekkelige detaljerte beskrivelse alle disse kreftene se at de er resultatet av konservative krefter, siden hver av disse makroskopiske kreftene er nettoresultatet av gradientene av mikroskopiske potensialer.^[13]^[16]

Sammenhengen mellom makroskopiske ikke-konservativ krefter og mikroskopiske konservative krefter beskrives ved detaljert behandling innenfor statistisk mekanikk. I makroskopiske lukkede systemer, virker ikke-konservativ krefter til å endre den indre energien til systemet, og er ofte forbundet med overføringen av varme. Ifølge termodynamikkens andre lov vil ikke-konservative krefter nødvendigvis resultere i energiovergang innenfor et lukkede system, fra ordnede til mer tilfeldige forhold ettersom entropien øker.^[13]^[16]

Translatoriske bevegelser

Rotasjon og dreiemoment

Forholdet mellom kraft (F), moment (τ), og drivmoment vektorer (p og L) i et roterende system.

Krefter som forårsaker at legmer med en viss utstrekning roterer er forbundet med dreiemoment ${\boldsymbol {\tau }}$ . Matematisk er moment forårsaket av en kraft $\mathbf {F}$ er definert i forhold til et vilkårlig referansepunkt som kryssproduktet:

{\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F}

der $\mathbf {r}$ er posisjonsvektoren til belastningspunktet i forhold til referansepunktet. Ofte kaller en dette produktet «kraft ganger arm».

Dreiemoment er en rotasjonsekvivalent til kraft, på den samme måte som vinkel er rotasjonsekvivalent for posisjon, vinkelhastigheten en ekvivalent til hastighet og drivmoment til bevegelsesmengde. Som en konsekvens av Newtons første lov om bevegelse finnes det treghetsmoment som gjør at alle legemer opprettholde sin rotasjonsbevegelse med mindre de blir påvirket av et ubalansert moment. Likeledes kan Newtons andre lov om bevegelse brukes til å utlede en analog ligning for den momentane vinkelakselerasjon til et stivt legeme:

{\boldsymbol {\tau }}=I{\boldsymbol {\alpha }}

der $I$ er treghetsmoment til legemet og ${\boldsymbol {\alpha }}$ er vektoren for vinkelakselerasjonen til legemet.

Dette gir en definisjon for treghetsmoment, som er en rotasjonsekvivalent for masse. I mer avanserte behandlinger av mekanikk, hvor rotasjonen i løpet av et tidsintervall er beskrevet, må treghetsmomentet være substituert med en treghetsmomenttensor. Når denne skal analyseres bestemmer den fullt ut egenskapene til rotasjonen, inkludert presesjon og nutasjon.

Ekvivalent med Newtons andre lov på differensial form gir en alternativ definisjon av dreiemoment:

{\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {dt} }},

der $\mathbf {L}$ er dreieimpuls til partikkelen.^[32]

Newtons tredje lov om bevegelse krever at alle objekter som øver dreiemomenter, selv utsettes for like og motsatte dreiemomenter,^[33] noe som også direkte impliserer at bevaring av drivmoment for lukkede systemer som opplever rotasjon på grunn av påvirkning av interne drivmomenter.

Sentripetalkraft

Under sleggekast utøves det en sentripetalkraft på kulen som får den til å følge en sirkelbane. Denne kraften er proporsjornal med massen og kvadratet av den tangensielle komponenten av fartenen, men omvent proporsjornal med radius til kulens bane.

For et legeme som akselererer i sirkulære bevegelser vil den ubalanserte kraften som virker på det være:^[34]

\mathbf {F} =-{\frac {mv^{2}{\hat {r}}}{r}}

der $m$ er massen til legemet, $v$ er hastigheten til det og $r$ er avstanden til sentrum av den sirkulær bane som det beskriver og ${\hat {r}}$ er en enhetsvektor som peker i radial retning utover fra sentrum. Dette betyr at den ubalanserte sentripetalkraften som utøves på et hvilken som helst legeme alltid er rettet mot sentrum av dets kurvebane. Slike krefter virker vinkelrett på hastighetsvektoren som er knyttet til bevegelsen av en gjenstand, og endrer derfor ikke farten til legemet. Derimot endrer den konstant retningen til hastighetsvektoren, selv om altså selve størrelsen av hastigheten er den samme. Den ubalanserte kraften som akselererer et legeme kan dekomponeres i en komponent som er perpendikulær til banen, og en som er tangentiell til banen. Dette gir både tangential kraft, som akselererer legemet ved enten å bremse det ned eller akselrerer det opp, og radial (sentripetal) kraft, som skifter retning.^[13]^[16]

På sitt enkleste kan sentripetalkraftens absoluttverdi skrives slik:

F=m{v^{2} \over r}

forutsatt at farten og hastigheten er konstant. Det er forøvrig vanlig å definere leddet etter massen $m$ i formelen som (absoluttverdien) av sentripetalakselerasjonen:

\ a={\frac {v^{2}}{r}},

også her under forutsetning om konstante verdier.

Kraft i den spesielle relativitetsteorien

Newtons bevegelseslover holdt seg uforandret i nesten tre hundre år før de ble forbedret.^[10] Ved begynnelsen av det 1900-tallet utviklet Albert Einstein sin relativitetsteori som beskriver virkningen av krefter på objekter med økende bevegelsesmengde nær lysets hastighet. Teorien ga også innsikt i de krefter som produseres av gravitasjon og treghet.

I henhold til den spesielle relativitetsteorien er masse og energi ekvivalente størrelser (som kan sees ved å beregne det arbeidet som kreves for å akselerere et legeme). Når et legemes hastigheten øker, øker også dets energi og dermed dens masseekvivalent (bevegelsesmengde). Det kreves derfor mer kraft for å akselerere det samme massen ved stor hastighet, enn den gjorde ved en lavere hastighet. Newtons andre lov

\mathbf {F} =\mathrm {d} \mathbf {p} /\mathrm {d} t

er gyldig fordi det er en matematisk definisjon.^[25]^:855–876 Men for å være konservert, må relativistisk bevegelsesmengde omdefineres slik:

\mathbf {p} ={\frac {m_{0}\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}}

hvor

\mathbf {v}

er hastigheten,

c

er lysets hastighet, og

m_{0}

er hvilemassen.

Det relativistiske uttrykket som knytter kraft og akselerasjon til en partikkel med konstant ikke-null hvilemasse $m$ som beveger seg i $x$ retning er:

F_{x}=\gamma ^{3}ma_{x}\,

F_{y}=\gamma ma_{y}\,

F_{z}=\gamma ma_{z}\,

hvor den såkalte Lorentz-faktoren benyttes:

\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}.

^[35]

I den tidlige utviklingen til relativistisk fysikk ble uttrykkene $\gamma ^{3}m$ og $\gamma m$ ble kalt longitudinal og transversal masse. Den relativistiske kraften produserer ikke en konstant akselerasjon, men en stadig avtagende akselerasjon etter som gjenstanden nærmer seg med lysets hastighet. Merk at $\gamma$ er udefinert for en partikkel med en ikke-null hvilemasse ved lysets hastighet, og teorien gir ingen prediksjon ved den hastigheten.

Hvis $v$ er svært liten i forhold til $c$ , vil dermed $\gamma$ være svært nær 1 og dermed er

F=ma

en nær tilnærming. Selv for bruk i relativistiske sammenhenger kan en imidlertid gjenopprette formen

F^{\mu }=mA^{\mu }\,

ved bruk av firevektorer. Dette forholdet er riktig i relativistisk sammenheng når $F^{\mu }$ er en firerkraft, $m$ er hvilemasse, og $A^{\mu }$ er firerakselerasjon.^[36]

Kraft i kvantemekanikk

Ti viktige bidragsytere til kvantemekanikken: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger og Richard Feynman.

Utdypende artikler: Kvantemekanikk og Paulis eksklusjonsprinsipp

Fra kontinuerlige til diskrete krefter

Med moderne innsikt i kvantemekanikk og teknologi som kan akselerere partikler nær lysets hastighet, har en via partikkelfysikken utviklet Standardmodellen for å beskrive krefter mellom partikler som er mindre enn atomer. Standardmodellen forutsier at utveksling av partikler som kalles gaugebosoner er den grunnleggende årsak til at krefter frigjøres og absorberes. Bare fire viktigste interaksjoner er kjent, etter avtagende styrke er dette: Sterk-, elektromagnetisk-, svak- og gravitasjonskraft.^[13]^:2–10^[16]^:79 Observasjoner innenfor Høyenergi partikkelfysikk som gjort i løpet av 1970 og 1980 bekreftet at de svake og elektromagnetiske krefter er uttrykk for en mer grunnleggende elektrosvak vekselvirkning.^[37]

Begrepet «kraft» beholder sin mening innenfor kvantemekanikk, selv om en nå arbeider med operatører i stedet for klassiske variabler, og fysikken beskrives av Schrödinger-ligningen i stedet for klassisk mekanikk. Dette har den konsekvens at resultatene av en måling nå ofte er «kvantifisert», det vil si at de forekommer i diskrete størrelser. Det er selvsagt vanskelig å tenke seg i forbindelse med krefter. Imidlertid vil potensialet $V(x,y,z)$ , eller felter, hvorfra de krefter som vanligvis kan utledes vil bli behandlet på lignende måte som klassiske posisjonsvariable, det vil si som $V(x,y,z)\to {\hat {V}}({\hat {x}},{\hat {y}},{\hat {z}})$ . Dette blir annerledes bare innenfor rammen av kvantefeltteori, hvor disse feltene også blir kvantifisert.

Allerede i kvantemekanikk er det en «påminnelse», nemlig at de partikler som virker inn på hverandre ikke bare har en romlig variabel, men også en diskret indre dreiemoment-lignende variabel kalt spinn, gitt av Paulis eksklusjonsprinsipp om rom og spinnvariabler. Avhengig av verdien av spinnet, er identiske partikler delt inn i to ulike klasser, nemlig fermioner og bosoner. Hvis to identiske fermioner (for eksempel elektroner) har et symmetrisk spinnfunksjon (for eksempel parallelle spinn) må de romlige variabler være asymmetriske. Det vil si at de utelukker hverandre fra sine plasser, mye som om det var en frastøtende kraft. Vice versa det vil si at for antiparallelle spinn må posisjons variablene være symmetrisk (det vil si den tilsynelatende kraften må være tiltrekkende). Således vil det i tilfelle av to fermioner være en strengt negativ korrelasjon mellom romlige- og spinnvariabler, mens for to bosoner (for eksempel kvanter av elektromagnetiske bølger, fotoner) er korrelasjonen strengt positiv. Dermed mister begrepet «kraft» en del av sin mening.

Feynman-diagram

Feynman-diagram for nedbryting av et nøytron til et proton. W-boson er mellom to hjørnene indikerer en frastøting.

Foto: Joel Holdsworth

I moderne partikkelfysikk er krefter og akselerasjonen av partikler forklart som en matematisk biprodukt ved utveksling av bevegelsesmengde-førende Gauge-bosoner. Med utviklingen av kvantefeltteori og generelle relativitet ble det innsett at kraft er et overflødig begrep som stammer fra bevaring av bevegelsesmengde (4-bevegelsesmengde) i relativitetsteorien og bevegelsesmengde av virtuelle partikkeler i Kvanteelektrodynamikk). Bevaring av bevegelses kan direkte avledes av homogenitet eller symmetri av rom som vanligvis blir ansett som mer fundamental enn konseptet med en kraft. Dermed er de nå kjente fundamentalkreftene ansett som mer presist å være «fundamentalinteraksjoner».^[37]^:199–128

Når partikkel A avgir (skaper) eller absorberer (tilintetgjør) en virtuelle partikkel B, vil bevaring av bevegelsesmengden resulterer i rekylen av partikkel A fører til frastøting eller tiltrekning mellom partiklene A og A' til utveksling av B. Denne beskrivelsen gjelder for alle krefter som oppstår fra fundamentale interaksjoner. Avanserte matematiske beskrivelser er nødvendig for å forutsi fullt ut det nøyaktig resultat av slike interaksjoner. Derimot er det begrepsmessig enkelt å beskrive slike interaksjoner gjennom bruk av Feynman-diagram. I et Feynman-diagram er hver enkelt partikkel representert som en rett linje (verdenslinje) som går gjennom tiden, noe som normalt øker opp eller til høyre i diagrammet. Materie og anti-materiepartikler er identiske med unntak av deres forplantningsretning gjennom Feynman-diagrammet. Verdenslinjer av partikler som skjærer hverandre i interaksjonvertikaler, og Feynman-diagrammet representerer en hvilken som helst kraft som oppstår fra en vekselvirkning som forekommer ved toppunktet med en tilhørende umiddelbar endring i retningen av partikkels verdenslinje. Gauge-bosoner emiteres borte fra toppunktet som bølgete linjer, og i tilfelle av virtuelle partikkel utveksling absorberes disse på et tilstøtende toppunkt.^[38]

Nytten av Feynman-diagram er at andre typer fysiske fenomener som er en del av det generelle bildet av fundamentalkreftene, men er konseptuelt atskilt fra krefter, også kan beskrives ved hjelp av de samme reglene. For eksempel kan et Feynman-diagram beskrive i konsis detalj hvordan et nøytron nedbrytes til et elektron, proton og nøytrino, en interaksjon mediert av den samme gauge-bosonet som er ansvarlig for den svake kjernekraften.^[38]

De fundamentale kreftene

De fire fundamentale kreftene og forsøket på en forening

Alle kreftene i universet er basert på fire fundamentalkrefter. Den sterk- og svakekjernekrefter er krefter som bare virker på svært korte avstander, og er ansvarlig for samspillet mellom subatomære partikler, inkludert nukleoner og sammensatte nukleoner. Den elektromagnetiske kraften virker mellom elektrisk ladninger, og gravitasjonskraft virker mellom masseer. Alle andre krefter i naturen utledes fra disse fire fundamentalkreftene. For eksempel er friksjon en manifestasjon av den elektromagnetiske kraften som virker mellom atomer mellom to flater, samt Paulis eksklusjonsprinsipp (Pauliprinsippet),^[39] som ikke tillater atomer å passere gjennom hverandre. Tilsvarende er krefter i en fjær som modelleres etter Hookes lov, egentlig et resultat av elektromagnetiske krefter og eksklusjonsprinsippet som virker sammen for å returnere et objekt tilbake til sin likevekts stilling. Og sentrifugal kreftene er akselerasjons kreftene som oppstår bare på grunn av akselerasjonen av et roterende referansesystem.^[13]^:12-11^[16]^:359

Utvikling av grunnleggende teorier for krefter gikk langs linjene av forening av ulike ideer. For eksempel forente Isaac Newton den kraften som er ansvarlig for at gjenstander faller på overflaten av jorden, med kraften som er ansvarlig for banene til planetene i sin universelle gravitasjonsteori. Michael Faraday og James Clerk Maxwell vist at elektriske og magnetiske krefter ble forent gjennom en konsistent teori om elektromagnetisme. På 1900-tallet førte utvikling av kvantemekanikk til en moderne forståelse av at de første tre fundamentale kreftene (alle unntatt gravitasjon) er manifestasjoner av materie (fermioner) i samspill med utveksling av virtuell partikkeler kalt Gauge-bosoner.^[40] Standardmodellen for partikkelfysikk tar gitt en likhet mellom kreftene og ledet forskere til å forutsi forenelighet mellom de svake og elektromagnetiske krefter i teorien om elektrosvak vekselvirkning som senere er bekreftet ved observasjoner. Den fullstendige formulering av standardmodellen predikerer en hittil uobservert Higgs mekanisme, men observasjoner som nøytrinooscillasjoner tyder på at standardmodellen er ufullstendig. En storforenet teori slik at for kombinasjonen av elektrosvak vekselvirkning med den sterke kraften holdes frem som en mulighet med kandidatteorier som supersymmetri er foreslått å imøtekomme noen av de utestående uløste problemer i fysikk. Fysikere forsøker fortsatt å utvikle en konsekvent forening mellom modeller som skal kombinere alle de fire fundamentalkreftene i Teorien om alt. Einstein prøvd og feilet med dette arbeidet, men for tiden er den mest populære tilnærming for å svare på dette spørsmålet strengteori.^[37]^:212–219

**De fire fundamentalkreftene i naturen**^[41]
Egenskap/Interaksjon	Gravitasjon	Svak	Elektromagnetisk	Sterk
Egenskap/Interaksjon	Gravitasjon	(Elektrosvak)		Fundamental	Gjenværende
Virker på:	Masse - Energi	Svak ladning	Elektrisk ladning	Fargeladning	Atomær nukleon
Partikler opplever:	Alle	Kvarker, leptoner	Elektrisk ladet	Kvarker, Gluoner	Hadroner
Partikler formidler:	Graviton (enda ikke observert)	W⁺ W⁻ Z⁰	γ	Gluoner	Mesoner
Styrke i skala som kvarker:	10⁻⁴¹	10⁻⁴	1	60	Ikke aktuelt for kvarker
Styrke i skala med protoner/nøytroner:	10⁻³⁶	10⁻⁷	1	Ikke aktuelt for hadroner	20

Gravitasjonskraft

Utdypende artikkel: Tyngdekraft

Bilder av en fritt fallende basketball tatt med stroboskop med 20 blink per sekund. Distanseenhetene til høyre er multipler av omtrent 12 millimeter. Basketball starter i ro. På tidspunktet for det første blinket (avstand null) der den slippes, hvoretter antall enheter den faller er lik kvadratet av antall blink.

Foto: Michael Maggs

Det som nå kalles tyngdekraften ble ikke identifisert som en universell kraft før Isaac Newton gjorde sitt banebrytende arbeid. Før Newton ble tendensen til gjenstander til å falle mot jorda ikke forstått til å ha noen knytning til bevegelsen av himmellegemene. Galilei var medvirkende til å beskrive egenskapene til fallende gjenstander ved å bestemme at akselerasjonen til alle legemer i fritt fall var konstant og uavhengig av massen til legemet. I dag er tyngdeakselerasjonen mot jordoverflaten vanligvis definert som $\mathbf {g}$ og har en størrelse på cirka 9,81 meter per sekund i andre (ved havnivå og kan variere avhengig av geografisk plassering), og peker mot midten av jorden.^[42] Denne observasjonen betyr at tyngdekraften på et legeme på jordas overflate er direkte proporsjonal med dets masse. Dermed vil et legeme som har en masse på $m$ oppleve en kraft:

\mathbf {F} =m\mathbf {g}

I fritt fall er denne kraften uten motstand og derfor er netto kraft på legemet dets vekt. For legemer som ikke er i fritt fall er tyngdekraften motvirket av reaksjonskrefter fra deres støtteflater. For eksempel vil en person som står på bakken erfare null netto kraft, siden hans vekt er balansert med en normalkraft som utøves av bakken oppover.^[13]^[16]

Newtons bidrag til gravitasjonsteorien var å forene bevegelsene til himmellegemene, som Aristoteles hadde antatt var i en naturlig tilstand av konstant bevegelse, med fallbevegelse observert på Jorden. Han kom opp med det som for ettertiden er kjent som Newtons gravitasjonslov. Denne kunne redegjøre for de himmelske bevegelsene som hadde blitt beskrevet tidligere med Keplers lover.^[43]

Newton kom til å innse at virkningene av tyngdekraften kan observeres på forskjellige måter ved større avstander. Spesielt har Newton fastslått at akselerasjonen til månen i sin bane rundt jorden kunne tilskrives den samme tyngdekraften som virker på jordoverflaten ved at tyngdekraften avtar med kvadratet av avstanden fra jorden. Videre innså Newton at tyngdekraften er proporsjonal med massen av legemet som utøver tiltrekningen.^[43] Ved å kombinere disse ideene gis en formel som relaterer denne massen M og avstand r fra jorden til gravitasjonsakselerasjonen:

\mathbf {g} =-{\frac {GM}{r^{2}}}{\hat {r}}

hvor vektorens retningen er gitt av ${\hat {r}}$ , som er enhetsvektoren rettet utover fra midten av jorden.^[11]

I denne ligningen brukes en dimensjonal konstant $G$ til å beskrive den relative styrken av tyngdekraften. Denne konstante har kommet for å bli kjent som Newtons gravitasjonskonstant,^[44] skjønt verdien var ukjent i Newton levetid. Ikke før 1798 var Henry Cavendish i stand til å gjøre den første målingen av $G$ ved hjelp av en torsjonsfjær. Dette forsøket ble viden rapportert i datidens aviser som en måling av massen til jorden siden størrelsen av $G$ åpner for å løse likningen over for å beregne Jordens masse. Newton innså imidlertid at siden alle himmellegemer fulgt de samme bevegelseslover, måtte hans tyngdelov være universell. Kort sagt: Newtons lov om gravitasjon sier at kraften på et sfærisk legeme med masse $m_{1}$ på grunn av gravitasjonskraften fra massen $m_{2}$ er:

\mathbf {F} =-{\frac {GMm}{r^{2}}}{\hat {r}}

der $r$ er avstanden mellom de to legemes massesentra og ${\hat {r}}$ er enhetsvektoren som peker i retning bort fra midten av det første legemet mot midten av det andre legemet.^[11]

Denne formelen var kraftig nok til å stå som grunnlag for alle påfølgende beskrivelser av bevegelsene innenfor solsystemet opp til 1900-tallet. I løpet av den tiden ble sofistikerte metoder for Perturbasjons analyse oppfunnet,^[45] dette for å beregne avvikene i baneer på grunn av påvirkning fra flere legemer på en planet, for eksempel månen, kometer eller asteroideer. Formalismen var nøyaktig nok til å tillate matematikere å forutsi eksistensen av planet Neptun før det ble observert.^[46]

Det var bare banen til planeten Merkur at Newtons tyngdelov ikke virket til fullt ut å forklare. Noen astrofysikere forutså eksistensen av en annen planet (Vulkan) som ville forklare avviket, til tross for noen tidlige indikasjoner ble ingen slik planet funnet. Når senere Albert Einstein formulerte sin teori om generell relativitet vendte han sin oppmerksomhet til problemet med Merkurs bane og fant ut at hans teori ga en korreksjon, noe som kunne kompensere for avviket. Dette var første gang noen hadde vist at Newtons gravitasjonsteori var mindre riktig enn et alternativ.^[47]

Siden da har den generelle relativitetsteorien blitt anerkjent som den teorien som best forklarer gravitasjon. I generell relativitet er tyngdekraften ikke sett på som en kraft, men snarere objekter som beveger seg fritt i gravitasjonsfelt og reiser underlagt sin egen bevegelsesmengde i rette linjer i et buet romtid. Her i betydningen den korteste veien i romtid mellom to hendelser relatert til romtid. Fra perspektivet til legemet skjer all bevegelse som om det ikke var noen gravitasjon overhodet. Det er bare når den observere bevegelsen skjer i en global betydning at krumningen av romtid kan observeres, og kraften utledes fra legemets buete bane. Således er den lineære banen i romtid sett på som en buet linje i rommet, og det kalles for en ballistisk trajektor av legemet. For eksempel vil en basketball som kastes fra bakken beveger seg i en parabel som om den er i et enhetlig gravitasjonsfelt. Dens bane i romtid (når den ekstra dimensjonen blir tilført) er nesten en rett linje, svakt buet (med krumningsradius av størrelsesorden noen få lysår). Den tidsderiverte av den skiftende bevegelsesmengden til et legeme er hva en vil kalle «gravitasjonskraft».^[16]

Elektromagnetisk kraft

Elektrostatiske krefter virker på små papirbitter etter at en CD har fått et overskudd av elektrisk ladning.

Utdypende artikkel: Elektromagnetisme

Den elektrostatiske kraften ble først beskrevet i 1784 av Charles Augustin Coulomb som en kraft som eksisterte mellom to elektrisk ladninger.^[25]^:519 Egenskapene til den elektrostatiske kraften var at den varierte som en invers avstandskvadratlov i radial retning, der den oppstår både som tiltrekning og frastøting (det var iboende polaritet). Videre var kraften uavhengig av massen til de ladede legmene, samt at den fulgte superposisjonsprinsippet. Coulombs lov forener alle disse observasjonene til et konsist utsagn.^[48]

Etterfølgende matematikere og fysikere fant at konseptet om et elektrisk felt for å være nyttig for bestemmelse av den elektrostatiske kraften på en elektrisk ladning i ethvert punkt i rommet. Det elektriske feltet ble basert på bruk av en hypotetisk testladning hvor som helst i rommet, og deretter bruke Coulombs lov til å bestemme den elektrostatisk kraften.^[26]^{:4-6 to 4-8} Således er det elektriske felt $\mathbf {E}$ definert hvor som helst i rommet er definert som:

\mathbf {E} ={\mathbf {F}  \over {q}}

der $q$ er størrelsen av en hypotetisk testladning, $\mathbf {F}$ er kraften på testladninge.

Lorentzkraften virker på en partikkel (til venstre) eller en elektrisk strøm (til høyre) som beveger seg gjennom et magnetfelt.

I mellomtiden ble Lorentzkraften som er et fenomen relatert til magnetisme oppdaget å eksistere mellom to elektrisk strømmer. Den har samme matematiske struktur som Coulombs lov med forbehold om at strømmer i samme retning tiltrekker og i motsatte retninger virker frastøtende. I likhet med det elektriske felt, kan konseptet om et magnetfelt benyttes til å bestemme den magnetiske kraften $\mathbf {F}$ på en elektrisk strøm $I$ i ethvert punkt i rommet. I dette tilfelle er størrelsen av det magnetiske feltet \mathbf{B} (flukstetthet) bestemt til å være:

\mathbf {B} ={\mathbf {F}  \over {I\ell }}

der $\ell$ er lengden på den hypotetiske lederen som teststrømmen går gjennom. Det magnetiske feltet utøver en kraft på alle magneter, som for eksempel en kompassnål. Det faktum at Jordens magnetfelt er konsentrert tett langs jordens akse fører til at et kompass blir orientert i denne retningen, på grunn av den magnetiske kraften som trekke på kompassnålen.

Gjennom å kombinere definisjonen av elektrisk strøm som tidsendringstakten for en elektrisk ladning, kan en regel basert på vektor multiplikasjon kalt Lorentz lov etableres som beskriver kraften på en ladning som beveger seg i et magnetisk felt.^[26] Sammenhengen mellom elektrisitet og magnetisme åpner for beskrivelse av en enhetlig elektromagnetiske kraften som virker på ladninger. Denne kraften kan skrives som en sum av den elektrostatiske kraft (på grunn av det elektriske felt), og den magnetiske kraft (på grunn av det magnetiske felt). Fullt oppgitt er denne loven:

\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )

der $\mathbf {F}$ er den elektromagnetiske kraften, $q$ er størelsen av ladningen for partikkel, $\mathbf {E}$ er styrken av det elektriske feltet, $\mathbf {v}$ er hastigheten til partikkelen som er gitt av kryssproduktet med magnetfeltets flukstetthet ( $\mathbf {B}$ ).

Naturen til elektriske og magnetiske felt ble ikke fullt ut forstått før i 1864 da James Clerk Maxwell samlet en rekke tidligere teorier i et sett av 20 skalarlikninger, som senere ble omformulert til fire vektorligninger av Oliver Heaviside og Josiah Willard Gibbs.^[49] Maxwells likninger er en fullstendig beskrivelse av kildene til feltene som stasjonære og bevegelige ladninger, og interaksjoner av feltene selv. Dette førte til at Maxwell oppdage at elektriske og magnetiske felt kan være «selvgenererende» i form av en bølger som beveger seg med en hastighet som han regnet for å være lyshastigheten. Denne innsikten forent den gryende vitenskapen om elektromagnetisk teori med optikk og førte direkte til en fullstendig beskrivelse av elektromagnetisk spekter.^[50]

Men forsøk på å forene elektromagnetisk teori med to observasjoner, fotoelektrisk effekt, og ikke-eksistens av den såkalte ultrafiolette katastrofen, ble vanskelig. Gjennom arbeidet utført av ledende teoretiske fysikere, ble en ny teori om elektromagnetisme utviklet ved hjelp av kvantemekanikk. Denne siste modifikasjonen av elektromagnetisk teori førte til slutt til Kvanteelektrodynamikk, som fullt ut beskriver alle elektromagnetiske fenomener som blir formidlet av bølgepartikler som kalles fotoner. I kvanteelektrodynamikk er fotoner den grunnleggende utvekslingspartikkelen som beskrev alle interaksjoner knyttet til elektromagnetisme, inkludert den elektromagnetiske kraften.

Det er en vanlig misforståelse å tilskrive stivhet og fasthet i fast stoff til frastøting av like ladninger under påvirkning av den elektromagnetiske kraften. Men disse egenskapene skyldes faktisk Pauliprinsippet. Siden elektroner er fermioner, kan de ikke okkupere samme kvantemekaniske tilstand som andre elektroner. Når elektronene i et materiale er tett pakket sammen, er det ikke nok lavere energinivåer i form av kvantemekaniske tilstander for dem alle, så noen av dem må være i høyere energitilstander. Dette betyr at det trengs energi for å pakke dem sammen. Selv om denne effekten er manifestert makroskopisk som en strukturell kraft, er det teknisk bare et resultat av eksistensen av et begrenset sett av elektrontilstander.

Sterk kjernekraft

Det er to «kjernekrefter» som det i dag er vanlig å beskrive som interaksjoner som beskrives i den del av kvanteteorier som omhandler partikkelfysikk. Den sterke kjernekraften^[25]^:940 er kraften som er ansvarlig for den strukturelle integriteten til atomkjernene mens svak kjernekraft^[25]^:951 er ansvarlig for nedbrytning av visse nukleoner til leptoner og andre typer hadroner.^[13]^[16]

Den sterke kjernekraften er i dag forstått å representere interaksjon mellom kvarker og gluoner s som er beskrevet av teorien om kvantekromodynamikk^[51] Den sterke kjernekraft er en fundamentalkraft formidlet av gluoner, virker på kvarker, antikvarker, og gluoner selv. Den sterk kjernekraft er «sterkeste» av de fire fundamentale kreftene, derav navnet.

Den sterke kjernekraften virker bare direkte på elementærpartikler. Imidlertid er en rest av den kraften som observert mellom hadroner. Det mest kjente eksempel er den kraften som virker mellom nukleoner i atomkjerner som nukleærkraft. Her virker den sterk kjernekraften indirekte, overføres som gluoner, som utgjør en del av de virtuelle pi og rho mesoner, som klassisk overfører kjernekraften. De mange mislykkede søk etter frie kvarer har vist at elementærpartiklene som er berørt ikke er direkte observerbare. Dette fenomenet kalles fargesperring.

Svak kjernekraft

Den svake kjernekraft har sitt opphav i utveksling av tunge W- og Z-bosoner. Den mest kjente effekten er betahenfall (av nøytroner i atomkjerner) og den tilhørende radioaktivitet. Ordet «svak» er på grunn av det faktum at feltstyrken er rundt 10¹³ ganger mindre enn den for sterk kjernekraft. Likevel er den sterkere enn tyngdekraften over korte avstander. En konsistent elektrosvak teorien har også blitt utviklet, noe som viser at elektromagnetiske krefter og den svake kjernekraft er umerkbar ved temperaturer på i overkant av cirka 10¹⁵ Kelvin. Slike temperaturer har blitt undersøkt i moderne partikkelakseleratorer og viser forholdene i universet i de tidlige øyeblikk av Big Bang.

Måling av kraft

En skålvekt sammenligner tyngdekraften som virker på et legeme med et annet legeme med kjent masse som kalles lodd.

Foto: Poussin jean

En mye brukt kraftmåler er vektstangen. Den virker slik at en ukjent kraft sammenlignes med en kjent styrke. I det enkleste tilfellet brukes en vekt med armer som enten er like lange, eller ulik lange armer. For eksempel kan vekten av et legeme med kjent masse (kjent vekt) i den ene vektarmen, sammenlignes med kraften som virker på den andre armen som er påvirket av kraft med ukjent størrelse. I tilknytning til vektarmene kan det være en skala som er gradert med newton eller eventuelt enn annen måleenhet. Om det er en vekt for måling av masse er skalaen gradert i kg, som er avledet av vekten.

En kraft kan bestemmes på forskjellige måter ved deformasjon på et objekt som følge av den. Mye brukt er endringen av lengden til en fjær. Mye brukt er fjærvekter slik som vist i illustrasjonen til høyre. Her er det Hookes lov som kommer til anvendelse ved at lengdeutvidelsen av fjæren vil være proporsjonal med kraften:

\mathbf {F} =-k\Delta \mathbf {x}

hvor $k$ er fjærkonstanten som er gitt av selve fjæren og $\Delta \mathbf {x}$ er lengdeendringen til fjæren.

En kraft som virker på et legeme som beveger seg kan bestemmes ved at en måler tilbakelagt strekning over tid. Om legemets masse er kjent kan en benytte Newtons andre lov, altså $F=m\cdot a$ , der $F$ er kraft, $m$ er massen og $a$ er akselerasjonen. Målingen blir enklest om akselerasjonen er konstant.

En mye brukt metode innenfor teknologiske og fysiske sammenhenger er måling av elektrisk motstand i såkalte strekklapper. En strekklapp klistres på for eksempel en stålaksling som utsettes for kraft slik at den strekkes. Strekklappen vil følge med denne bevegelsen og motstanden som måles vil være proporsjonal med kreftene som virker.

Atomkraftmikroskop er et spesielt instrument som brukes til å målinger på makroskopisk nivå.

Størrelsen av krefter i forskjellige sammenhenger

Vekten av et eple er cirka 1 N

Foto: Lily.Smith

Gravitasjonskraften er generelt den svakeste av de fire kreftene i naturen. Den svakeste kraften en kjenner til er gravitasjonskreftene mellom et proton og et elektron i et hydrogenatom som er på 3,6×10⁻⁴⁷ N.^[52] I den motsatte enden av kjente krefter er gravitasjonskraften mellom solen og Sagittarius A* som er på 1,2×10⁴⁴ N. For øvrig er Sagittarius A* en ekstremt lyssterk og kompakt radioaktiv kilde i Melkeveiens sentrum.

Av mer kjente størrelser i dagliglivet er vekten av et eple 1 N,^[53] og vekten av en liter vann (1 kg) 9,81 N.

Se også

Noter

Type nummerering

^ «Det er viktig å merke seg at en ikke kan utlede et generelt uttrykk Newtons andre lov for variable massesystemer ved å behandle massen i $F=dP/dt=d(Mv)$ som en variabel... Vi kan bruke $F=d(P/dt)$ å analysere variable massesystemer bare hvis vi bruker den for hele systemet med konstant masse å ha deler blant disse der det foregår en utveksling av masse.»^[14]
^ Et unntak fra dette er:Landau, L. D.; Akhiezer, A. I.; Lifshitz, A. M. (196). General Physics; mechanics and molecular physics (First English utg.). Oxford: Pergamon Press. ISBN 0-08-003304-0. Oversatt av: J. B. Sykes, A. D. Petford, og C. L. Petford. Library of Congress Catalog Number 67-30260. I kapittel 7, side 12-14, denne boken definerer kraft som dp/dt.
^ «Enhver enkelt kraft er bare ett aspekt av et gjensidig samspill mellom to legemer.»^[20]

Referanser

^ Wandmacher, Cornelius; Johnson, Arnold (1995). Metric Units in Engineering. ASCE Publications. s. 15. ISBN 0-7844-0070-9.
^ ^a ^b Heath, T.L. The Works of Archimedes (1897). The unabridged work in PDF form (19 MB).
^ Lang, Helen S. (1998). The order of nature in Aristotle's physics : place and the elements (1. publ. utg.). Cambridge: Cambridge Univ. Press. ISBN 9780521624534.
^ Hetherington, Norriss S. (1993). Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives. Garland Reference Library of the Humanities. s. 100. ISBN 0-8153-1085-4.
^ Wildberg, Christian (11. mars 2003). «John Philoponus». The Stanford Encyclopedia of Philosophy.
^ ^a ^b Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5
^ Machamer, Peter (4. mars 2005). «Galileo Galilei». The Stanford Encyclopedia of Philosophy.
^ Hugo D. Young og Roger A. Freedman (2008). University Physics (på engelsk) (XII utg.). Addison Wesley. s. 113–114. ISBN 978-0-321-50130-1.
^ Steve Connor. «The core of truth behind Sir Isaac Newton's apple». www.independent.co.uk. Besøkt 11. januar 2017.
^ ^a ^b ^c ^d ^e ^f ^g University Physics, Sears, Young & Zemansky, pp.18–38
^ ^a ^b ^c ^d ^e ^f ^g Newton, Isaac (1999). The Principia Mathematical Principles of Natural Philosophy. Berkeley: University of California Press. ISBN 0-520-08817-4.
^ Carl Hoefer: Causal Determinism. Artikel in der Stanford Encyclopedia of Philosophy (englisch).
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^æ Feynman volume 1
^ Halliday, Resnick, Krane: Physics v. 1, side 199.
^ Howland, R. A. (2006). Intermediate dynamics a linear algebraic approach (Online-Ausg. utg.). New York: Springer. s. 255–256. ISBN 9780387280592.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x Kleppner & Kolenkow 2010
^ Jammer, Max (1999). Concepts of force : a study in the foundations of dynamics (Facsim. utg.). Mineola, N.Y.: Dover Publications. s. 220–222. ISBN 9780486406893.
^ Noll, Walter (April 2007). (pdf). Carnegie Mellon University http://www.math.cmu.edu/~wn0g/Force.pdf. Besøkt 28. oktober 2013. Manglende eller tom |tittel= (hjelp)
^ C. Hellingman (1992). «Newton's third law revisited». Phys. Educ. 27 (2): 112–115. Bibcode:1992PhyEd..27..112H. doi:10.1088/0031-9120/27/2/011. «Newton sier i Principia : Det er ikke en kraft fra solen som tiltrekker Jupiter, og en annen fra Jupiter som tiltrekker Solen; men det er en kraft der Solen og Jupiter gjensidig forsøke å komme nærmere sammen.»
^ Halliday, Resnick, Krane: Physics v. 1 side 78-79.
^ Dr. Nikitin (2007). «Dynamics of translational motion». Arkivert fra originalen 11. september 2009. Besøkt 4. januar 2008.
^ «Introduction to Free Body Diagrams». Physics Tutorial Menu. University of Guelph. Arkivert fra originalen 16. januar 2008. Besøkt 2. januar 2008. «Arkivert kopi». Arkivert fra originalen 16. januar 2008. Besøkt 15. januar 2017.
^ Henderson, Tom (2004). «The Physics Classroom». The Physics Classroom and Mathsoft Engineering & Education, Inc. Arkivert fra originalen 1. januar 2008. Besøkt 2. januar 2008. «Arkivert kopi». Arkivert fra originalen 1. januar 2008. Besøkt 15. januar 2017.
^ «Static Equilibrium». Physics Static Equilibrium (forces and torques). University of the Virgin Islands. Arkivert fra originalen 19. oktober 2007. Besøkt 2. januar 2008.
^ ^a ^b ^c ^d ^e Cutnell & Johnson 2003
^ ^a ^b ^c Feynman volume 2
^ Nave, Carl Rod. «Elasticity». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.
^ Mallette, Vincent (1982–2008). «Inwit Publishing, Inc. and Inwit, LLC – Writings, Links and Software Distributions – The Coriolis Force». Publications in Science and Mathematics, Computing and the Humanities. Inwit Publishing, Inc. Besøkt 4. januar 2008.
^ Hibbeler, Russell C. (2010). Engineering Mechanics, 12th edition. Pearson Prentice Hall. s. 222. ISBN 0-13-607791-9.
^ Singh, Sunil Kumar (25. august 2007). «Conservative force». Connexions. Besøkt 4. januar 2008.
^ Davis, Doug. «Conservation of Energy». General physics. Besøkt 4. januar 2008.
^ Nave, Carl Rod. «Newton's 2nd Law: Rotation». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.
^ Fitzpatrick, Richard (7. januar 2007). «Newton's third law of motion». Besøkt 4. januar 2008.
^ Nave, Carl Rod. «Centripetal Force». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.
^ «Seminar:Visualizing Special Relativity». The Relativistic Raytracer. Besøkt 4. januar 2008.
^ Wilson, John B. «Four-Vectors (4-Vectors) of Special Relativity: A Study of Elegant Physics». The Science Realm: John's Virtual Sci-Tech Universe. Arkivert fra originalen 26. juni 2009. Besøkt 4. januar 2008. «Arkivert kopi». Archived from the original on 26. juni 2009. Besøkt 23. februar 2021. CS1-vedlikehold: Uheldig URL (link)
^ ^a ^b ^c Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books USA. ISBN 0-679-74408-8.
^ ^a ^b Shifman, Mikhail (1999). ITEP lectures on particle physics and field theory. World Scientific. ISBN 981-02-2639-X.
^ Nave, Carl Rod. «Pauli Exclusion Principle». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.
^ «Fermions & Bosons». The Particle Adventure. Arkivert fra originalen 18. desember 2007. Besøkt 4. januar 2008. «Arkivert kopi». Archived from the original on 18. desember 2007. Besøkt 15. januar 2017. CS1-vedlikehold: Uheldig URL (link)
^ «Standard model of particles and interactions». Contemporary Physics Education Project. 2000. Arkivert fra originalen 2. januar 2017. Besøkt 2. januar 2017.
^ Cook, A. H. (1965). «A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory». Nature. 208 (5007): 279. Bibcode:1965Natur.208..279C. doi:10.1038/208279a0.
^ ^a ^b Young, Hugh; Freedman, Roger; Sears, Francis and Zemansky, Mark (1949) University Physics. Pearson Education. Side 59–82
^ «Sir Isaac Newton: The Universal Law of Gravitation». Astronomy 161 The Solar System. Besøkt 4. januar 2008.
^ Watkins, Thayer. «Perturbation Analysis, Regular and Singular». Department of Economics. San José State University. Arkivert fra originalen 10. februar 2011. Besøkt 15. januar 2017.
^ Kollerstrom, Nick (2001). «Neptune's Discovery. The British Case for Co-Prediction.». University College London. Arkivert fra originalen 11. november 2005. Besøkt 19. mars 2007.
^ Siegel, Ethan (20. mai 2016). «When Did Isaac Newton Finally Fail?». Forbes. Besøkt 3. januar 2017.
^ Coulomb, Charles (1784). «Recherches théoriques et expérimentales sur la force de torsion et sur l'élasticité des fils de metal». Histoire de l'Académie Royale des Sciences: 229–269.
^ Scharf, Toralf (2007). Polarized light in liquid crystals and polymers. John Wiley and Sons. s. 19. ISBN 0-471-74064-0. , Chapter 2, p. 19
^ Duffin, William (1980). Electricity and Magnetism, 3rd Ed. McGraw-Hill. s. 364–383. ISBN 0-07-084111-X.
^ Stevens, Tab (10. juli 2003). «Quantum-Chromodynamics: A Definition – Science Articles». Arkivert fra originalen 16. oktober 2011. Besøkt 4. januar 2008. «Arkivert kopi». Arkivert fra originalen 16. oktober 2011. Besøkt 15. januar 2017.
^ Hugh D. Young, University Physics 4th Ed, 1992, Addison-Wesley Publishing Co, Inc.
^ Glenn Elert. «Weight of an Apple». The Physics Factbook. Besøkt 11. januar 2017.

Litteratur

Corben, H.C. (1994). Classical Mechanics. New York: Dover publications. s. 28–31. ISBN 0-486-68063-0.
Cutnell, John D.; Johnson, Kenneth W. (2003). Physics, Sixth Edition. Hoboken, New Jersey: John Wiley & Sons Inc. ISBN 0471151831.
Feynman, Richard P.; Leighton; Sands, Matthew (2010). The Feynman lectures on physics. Vol. I: Mainly mechanics, radiation and heat (New millennium utg.). New York: BasicBooks. ISBN 978-0465024933.
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2010). The Feynman lectures on physics. Vol. II: Mainly electromagnetism and matter (New millennium utg.). New York: BasicBooks. ISBN 978-0465024940.
Halliday, David; Resnick, Robert; Krane, Kenneth S. (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
Kleppner, Daniel; Kolenkow, Robert J. (2010). An introduction to mechanics (3. print utg.). Cambridge: Cambridge University Press. ISBN 0521198216.
Parker, Sybil (1993). «force». Encyclopedia of Physics. Ohio: McGraw-Hill. s. 107,. ISBN 0-07-051400-3.
Sears F., Zemansky M. & Young H. (1982). University Physics. Reading, Massachusetts: Addison-Wesley. ISBN 0-201-07199-1.
Serway, Raymond A. (2003). Physics for Scientists and Engineers. Philadelphia: Saunders College Publishing. ISBN 0-534-40842-7.
Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th utg.). W. H. Freeman. ISBN 0-7167-0809-4.
Verma, H.C. (2004). Concepts of Physics Vol 1. (2004 Reprint utg.). Bharti Bhavan. ISBN 8177091875.

Eksterne lenker

(en) Forces (physics) – kategori av bilder, video eller lyd på Commons

Wiktionary: Kraft – ordbokoppføring

[15] «Det er viktig å merke seg at en ikke kan utlede et generelt uttrykk Newtons andre lov for variable massesystemer ved å behandle massen i $F=dP/dt=d(Mv)$ som en variabel... Vi kan bruke $F=d(P/dt)$ å analysere variable massesystemer bare hvis vi bruker den for hele systemet med konstant masse å ha deler blant disse der det foregår en utveksling av masse.»^[14]

[18] Et unntak fra dette er:Landau, L. D.; Akhiezer, A. I.; Lifshitz, A. M. (196). General Physics; mechanics and molecular physics (First English utg.). Oxford: Pergamon Press. ISBN 0-08-003304-0. Oversatt av: J. B. Sykes, A. D. Petford, og C. L. Petford. Library of Congress Catalog Number 67-30260. I kapittel 7, side 12-14, denne boken definerer kraft som dp/dt.

[23] «Enhver enkelt kraft er bare ett aspekt av et gjensidig samspill mellom to legemer.»^[20]

[metric_units-1] Wandmacher, Cornelius; Johnson, Arnold (1995). Metric Units in Engineering. ASCE Publications. s. 15. ISBN 0-7844-0070-9.

[Archimedes-2] Heath, T.L. The Works of Archimedes (1897). The unabridged work in PDF form (19 MB).

[3] Lang, Helen S. (1998). The order of nature in Aristotle's physics : place and the elements (1. publ. utg.). Cambridge: Cambridge Univ. Press. ISBN 9780521624534.

[Hetherington-4] Hetherington, Norriss S. (1993). Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives. Garland Reference Library of the Humanities. s. 100. ISBN 0-8153-1085-4.

[5] Wildberg, Christian (11. mars 2003). «John Philoponus». The Stanford Encyclopedia of Philosophy.

[Galileo-6] Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5

[7] Machamer, Peter (4. mars 2005). «Galileo Galilei». The Stanford Encyclopedia of Philosophy.

[8] Hugo D. Young og Roger A. Freedman (2008). University Physics (på engelsk) (XII utg.). Addison Wesley. s. 113–114. ISBN 978-0-321-50130-1.

[9] Steve Connor. «The core of truth behind Sir Isaac Newton's apple». www.independent.co.uk. Besøkt 11. januar 2017.

[uniphysics_ch2-10] ^ ^a ^b ^c ^d ^e ^f ^g University Physics, Sears, Young & Zemansky, pp.18–38

[Principia-11] ^ ^a ^b ^c ^d ^e ^f ^g Newton, Isaac (1999). The Principia Mathematical Principles of Natural Philosophy. Berkeley: University of California Press. ISBN 0-520-08817-4.

[12] Carl Hoefer: Causal Determinism. Artikel in der Stanford Encyclopedia of Philosophy (englisch).

[FeynmanVol1-13] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^æ Feynman volume 1

[14] Halliday, Resnick, Krane: Physics v. 1, side 199.

[16] Howland, R. A. (2006). Intermediate dynamics a linear algebraic approach (Online-Ausg. utg.). New York: Springer. s. 255–256. ISBN 9780387280592.

[Kleppner-17] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x Kleppner & Kolenkow 2010

[19] Jammer, Max (1999). Concepts of force : a study in the foundations of dynamics (Facsim. utg.). Mineola, N.Y.: Dover Publications. s. 220–222. ISBN 9780486406893.

[20] Noll, Walter (April 2007). (pdf). Carnegie Mellon University http://www.math.cmu.edu/~wn0g/Force.pdf. Besøkt 28. oktober 2013. Manglende eller tom |tittel= (hjelp)

[21] C. Hellingman (1992). «Newton's third law revisited». Phys. Educ. 27 (2): 112–115. Bibcode:1992PhyEd..27..112H. doi:10.1088/0031-9120/27/2/011. «Newton sier i Principia : Det er ikke en kraft fra solen som tiltrekker Jupiter, og en annen fra Jupiter som tiltrekker Solen; men det er en kraft der Solen og Jupiter gjensidig forsøke å komme nærmere sammen.»

[22] Halliday, Resnick, Krane: Physics v. 1 side 78-79.

[24] Dr. Nikitin (2007). «Dynamics of translational motion». Arkivert fra originalen 11. september 2009. Besøkt 4. januar 2008.

[25] «Introduction to Free Body Diagrams». Physics Tutorial Menu. University of Guelph. Arkivert fra originalen 16. januar 2008. Besøkt 2. januar 2008. «Arkivert kopi». Arkivert fra originalen 16. januar 2008. Besøkt 15. januar 2017.

[26] Henderson, Tom (2004). «The Physics Classroom». The Physics Classroom and Mathsoft Engineering & Education, Inc. Arkivert fra originalen 1. januar 2008. Besøkt 2. januar 2008. «Arkivert kopi». Arkivert fra originalen 1. januar 2008. Besøkt 15. januar 2017.

[27] «Static Equilibrium». Physics Static Equilibrium (forces and torques). University of the Virgin Islands. Arkivert fra originalen 19. oktober 2007. Besøkt 2. januar 2008.

[Cutnell-28] Cutnell & Johnson 2003

[FeynmanVol2-29] Feynman volume 2

[30] Nave, Carl Rod. «Elasticity». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.

[31] Mallette, Vincent (1982–2008). «Inwit Publishing, Inc. and Inwit, LLC – Writings, Links and Software Distributions – The Coriolis Force». Publications in Science and Mathematics, Computing and the Humanities. Inwit Publishing, Inc. Besøkt 4. januar 2008.

[32] Hibbeler, Russell C. (2010). Engineering Mechanics, 12th edition. Pearson Prentice Hall. s. 222. ISBN 0-13-607791-9.

[33] Singh, Sunil Kumar (25. august 2007). «Conservative force». Connexions. Besøkt 4. januar 2008.

[34] Davis, Doug. «Conservation of Energy». General physics. Besøkt 4. januar 2008.

[35] Nave, Carl Rod. «Newton's 2nd Law: Rotation». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.

[36] Fitzpatrick, Richard (7. januar 2007). «Newton's third law of motion». Besøkt 4. januar 2008.

[37] Nave, Carl Rod. «Centripetal Force». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.

[38] «Seminar:Visualizing Special Relativity». The Relativistic Raytracer. Besøkt 4. januar 2008.

[39] Wilson, John B. «Four-Vectors (4-Vectors) of Special Relativity: A Study of Elegant Physics». The Science Realm: John's Virtual Sci-Tech Universe. Arkivert fra originalen 26. juni 2009. Besøkt 4. januar 2008. «Arkivert kopi». Archived from the original on 26. juni 2009. Besøkt 23. februar 2021. CS1-vedlikehold: Uheldig URL (link)

[final_theory-40] Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books USA. ISBN 0-679-74408-8.

[Shifman-41] Shifman, Mikhail (1999). ITEP lectures on particle physics and field theory. World Scientific. ISBN 981-02-2639-X.

[42] Nave, Carl Rod. «Pauli Exclusion Principle». HyperPhysics. University of Guelph. Besøkt 28. oktober 2013.

[43] «Fermions & Bosons». The Particle Adventure. Arkivert fra originalen 18. desember 2007. Besøkt 4. januar 2008. «Arkivert kopi». Archived from the original on 18. desember 2007. Besøkt 15. januar 2017. CS1-vedlikehold: Uheldig URL (link)

[44] «Standard model of particles and interactions». Contemporary Physics Education Project. 2000. Arkivert fra originalen 2. januar 2017. Besøkt 2. januar 2017.

[45] Cook, A. H. (1965). «A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory». Nature. 208 (5007): 279. Bibcode:1965Natur.208..279C. doi:10.1038/208279a0.

[uniphysics_ch4-46] Young, Hugh; Freedman, Roger; Sears, Francis and Zemansky, Mark (1949) University Physics. Pearson Education. Side 59–82

[47] «Sir Isaac Newton: The Universal Law of Gravitation». Astronomy 161 The Solar System. Besøkt 4. januar 2008.

[48] Watkins, Thayer. «Perturbation Analysis, Regular and Singular». Department of Economics. San José State University. Arkivert fra originalen 10. februar 2011. Besøkt 15. januar 2017.

[Neptdisc-49] Kollerstrom, Nick (2001). «Neptune's Discovery. The British Case for Co-Prediction.». University College London. Arkivert fra originalen 11. november 2005. Besøkt 19. mars 2007.

[50] Siegel, Ethan (20. mai 2016). «When Did Isaac Newton Finally Fail?». Forbes. Besøkt 3. januar 2017.

[Coulomb-51] Coulomb, Charles (1784). «Recherches théoriques et expérimentales sur la force de torsion et sur l'élasticité des fils de metal». Histoire de l'Académie Royale des Sciences: 229–269.

[52] Scharf, Toralf (2007). Polarized light in liquid crystals and polymers. John Wiley and Sons. s. 19. ISBN 0-471-74064-0. , Chapter 2, p. 19

[53] Duffin, William (1980). Electricity and Magnetism, 3rd Ed. McGraw-Hill. s. 364–383. ISBN 0-07-084111-X.

[54] Stevens, Tab (10. juli 2003). «Quantum-Chromodynamics: A Definition – Science Articles». Arkivert fra originalen 16. oktober 2011. Besøkt 4. januar 2008. «Arkivert kopi». Arkivert fra originalen 16. oktober 2011. Besøkt 15. januar 2017.

[Hugh_D._Young_1992-55] Hugh D. Young, University Physics 4th Ed, 1992, Addison-Wesley Publishing Co, Inc.

[56] Glenn Elert. «Weight of an Apple». The Physics Factbook. Besøkt 11. januar 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[a]

[15]

[16]

[b]

[17]

[18]

[19]

[c]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[14]

[20]