Raiz da unidade

Em matemática, as raízes n-ésimas da unidade, ou números de de Moivre, são todos os números complexos que resultam 1 quando são elevados a n. Raízes da unidade são usadas em muitas áreas da matemática, sendo especialmente importantes para a teoria dos números, para a representação de caráter em teoria dos grupos, e para a transformada discreta de Fourier. Pode-se demonstrar que estão localizados no círculo unitário do plano complexo e que nesse plano formam os vértices de um polígono regular de n lados com um vértice sobre 1.

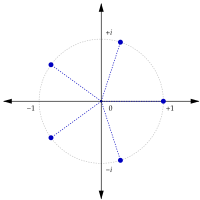
Raízes cúbicas da unidade no plano complexo		Raízes quintas da unidade no plano complexo

Uma raiz n-ésima da unidade é chamada de primitiva (ou seja, uma raiz primitiva n-ésima da unidade) quando ela não é também uma raiz m-ésima da unidade para m < n. Por exemplo, i é uma raiz quarta e raiz oitava da unidade, mas é apenas uma raiz quarta primitiva da unidade.

Definição

Diz-se que uma raiz n-ésima da unidade, onde n é um inteiro positivo (n = 1, 2, 3, …), é um número complexo z que satisfaça a equação

$z^{n}=1$,

que, pelo teorema fundamental da álgebra, possui $n$ raízes no conjunto $\mathbb {C}$ dos números complexos.

Soluções

Uma das soluções sempre será o número $1$, já que $1^{n}=1$ para qualquer $n$ inteiro positivo. As demais soluções podem ser obtidas reescrevendo o número $1$ de forma conveniente através da fórmula de Euler:

$e^{ix}=\cos \left(x\right)+{\text{i}}\,\operatorname {sen} \left(x\right).$

Substituindo-se $x=2\pi \mathrm {k}$, onde $k\in \mathbb {Z}$ obtém-se:

$e^{{\text{i}}(2\pi \mathrm {k} )}=\cos \left(2\pi \mathrm {k} \right)+{\text{i}}\,\operatorname {sen} \left(2\pi \mathrm {k} \right)=1$

Implicando que o número $1$ pode ser escrito da seguinte forma:

$1=e^{2\pi \mathrm {i} k}$

Resolve-se, então, a equação que define as raízes da unidade:

$z^{n}=1\implies z=1^{1 \over n}=(e^{2\pi \mathrm {i} k})^{1 \over n}=e^{2\pi \mathrm {i} k \over n}$

Então $z$ pode ser escrito como:

$z=\cos \left({2\pi \mathrm {k} \over n}\right)+{\text{i}}\,\operatorname {sen} \left({2\pi \mathrm {k} \over n}\right)$, $k\in \mathbb {Z}$

A princípio, tal expressão aponta para um número infinito de soluções. No entanto, dado a periodicidade das funções seno e cosseno, há mais de um $k$ associado a uma mesma raiz. De fato, há infinitos $k'$ associados a um mesmo valor de $z$ que seja dado por um valor principal $k$. A relação de congruência entre $k'$ e $k$ é, por análise:

$k'\equiv k{\pmod {n}}.$

Desse modo, a solução resume-se a $n$ raízes para $z$, dadas por:

$z_{k+1}=\cos \left({2\pi \mathrm {k} \over n}\right)+{\text{i}}\,\operatorname {sen} \left({2\pi \mathrm {k} \over n}\right),$

$k=0,1,2,...,n-1$

Propriedades aritméticas

Soma das raízes

A soma das raízes da unidade é igual a $0$, $\forall \,n\geqslant 2$. Uma maneira de provar isso, é utilizando a soma de uma progressão geométrica.

$\sum _{k=0}^{n-1}e^{2\pi {\text{i}}k \over n}$ $=e^{2\pi {\text{i}}.(0) \over n}+e^{2\pi {\text{i}}.(1) \over n}+\cdots +e^{2\pi {\text{i}}.(n-1) \over n}$ $=\underbrace {e^{2\pi {\text{i}}\cdot (0)/n}} _{1}\cdot {\cfrac {\overbrace {e^{2\pi {\text{i}}\cdot (n)/n}} ^{1}-1}{e^{2\pi {\text{i}}/n}-1}}$ $=0$

Outra maneira de provar essa propriedade, é considerar as relações de Girard. Observando o polinômio $z^{n}+0.z^{n-1}-1=0$ , é fácil notar que a soma das raízes é igual a $0$.

Produto das Raízes

Através das relações de Girard, pode-se deduzir que o produto das raízes é $1$ para $n$ ímpar e $-1$ para $n$ par.

Equação Ciclotômica

Ver artigos principais: Equação ciclotômica e Corpo ciclotômico

Teorema de Gauss-Wantzel

Carl Friedrich Gauss demonstrou que o problema de resolver a equação $x^{p}=1$, também denominada ciclotômica, pode ser reduzido a resolver uma série de equações quadráticas, para quando $p$ for um primo de Fermat, isto é, para quando for um primo e puder ser escrito como $p=2^{2^{n}}+1$, onde $n\in \mathbb {N}$. Pierre Laurent Wantzel provou posteriormente, em 1836, que tal condição não só é suficiente, mas necessária.

O teorema de Gauss-Wantzel possui um importante valor histórico por promover uma ligação entre análise complexa e geometria euclidiana, visto que implica na especificação de quais polígonos são construtíveis a partir de régua e compasso, problema milenar enfrentado pelos matemáticos desde a Grécia antiga. Nesse contexto, ele prova que o polígono de 17 lados, o heptadecágono, é construtível pelo número de lados ser um primo de Fermat, contrastando com polígonos menores como o heptágono e o eneágono, que não são construtíveis.

Bibliografia

• Lang, Serge (2002). Algebra, 3rd revised edition. Nova York: Springer-Verlag. ISBN 0-387-95385-X.