Abstract
In drug discovery, protonation states and tautomerization are easily overlooked. Through a Merck–Rutgers collaboration, this paper re-examined the initial settings and preparations for the Thermodynamic Integration (TI) calculation in AMBER Free-Energy Workflows, demonstrating the value of careful consideration of ligand protonation and tautomer state. Finally, promising results comparing AMBER TI and Schrödinger FEP+ are shown that should encourage others to explore the value of TI in routine Structure-based Drug Design.
Keywords: Protonation, Tautomerization, Free energy calculation, Thermodynamic integration, Free energy perturbation, Protein–ligand binding affinity
Introduction
Molecular modelling, especially free energy calculations, are widely implemented in predicting the protein–ligand binding affinities or at least ranking the order of the candidates in small molecule structure-based drug design (SBDD). Structure-based, in silico binding affinity prediction is playing a more and more important role in both pre-lead and lead optimization [1–6]. Rigorous alchemical methods such as Thermodynamic Integration (TI) and Free Energy Perturbation (FEP) have shown considerable success in making accurate predictions [1, 2, 4, 5]. However, the application of such approaches in structure-based virtual screening is obstructed for the non-expert users by the prerequisite of knowledge of the methods and parameter settings and reduced interest for experienced users due to tedious, time-consuming and error-prone setup.
The increasing demand for fast and accurate computational predictions draws attention to automate these free energy calculation methods. Several commercial and academic workflows have been developed to simplify the setups in recent years. Schrödinger MCPRO+ is a program built upon the MCPRO [7] application supporting lead optimization. It automates the setup of FEP calculation using Monte Carlo sampling. Schrödinger FEP+ [2] is a program which automates the setup of FEP using molecular dynamics (MD) simulations. Another tool FESetup [8] supports the setup of alchemical free energy such as TI and FEP utilizing Maximum Common Substructure Search (MCSS) mapping, and post-processing methods like Molecular Mechanics-Generalized Born Surface Area (MM-GBSA), Molecular Mechanics-Poisson Boltzmann Surface Area (MM-PBSA), Linear Interaction Energy (LIE) simulations for modelling packages-AMBER, GROMACS, Sire and NAMD. LOMAP [9] is a tool to systematically plan relative binding free energy calculations. It optimizes the ligand pair transformation maps by considering the structural similarity, properly treating rings and net charges, which reduce the error accumulation. Combining with recent developed python tools alchemical-setup.py [10] and alchemical-analysis.py [11], it provides a full tool sets for planning, setting up and analyzing relative free energy calculations in GROMACS. The PMX software [12] provides the setup of alchemical free energy calculations to determine binding free energy or protein stability resulting from amino acid mutation. The Binding Affinity Calculator (BAC) [13] automates the MM-PBSA calculations in AMBER for protein–ligand binding free energy predictions encompassing the entropic contribution from normal-mode analysis. The AMBER FEW program [14] provides command-line, multistep workflows to automate four scoring methods, MM-GBSA, MM-PBSA, LIE and TI and supports both protein–ligand [14] and membrane protein–ligand systems [15]. AMBER FEW program significantly reduces the amount of time to setup the calculations. Through a Merck–Rutgers collaboration, an in-house high quality free energy calculation platform has been built upon AMBER FEW at Merck, which not only provides access to the well-developed SBDD computational predictions of MMGBSA, MMPBSA, LIE and TI, but also facilitates adding new free energy calculations modules as they arise.
Protonation states and tautomerization are easily overlooked in drug discovery. In this work, we re-examined the same data set in the FEW study [14], scrutinized various parameter settings, and investigated the effect of correct protonation and suitable tautomerization on the calculated ligand binding affinity by using the TI workflow in AMBER FEW. To our knowledge, there is currently no comparison study between academic workflow AMBER FEW with commercial software Schrodinger FEP+ [2], an arising accurate prediction tool in industry and showing increasing success in drug design. Furthermore, we compared the performance of TI calculations using AMBER FEW with Schrödinger FEP calculations. We hope the current study would timely encourage the application of AMBER FEW TI workflow in structure-based drug design.
Methods
Structure preparation of FXa data set
The structures of ligand and receptor were carefully prepared based on the high resolution Factor Xa–L51a crystal complex structure (PDB code: 2RA0, resolution: 2.3Å) with no missing residues. The structure of Factor Xa was first separated from the crystal complex with all crystallographic water molecules. Back mutation was modeled for L88V mutation in the L chain. N-methyl-capping group (NME) was added to the C-termini of both chain A and L, while Acetyl-capping group (ACE) was only added to the N-termini of the chain L which is in the exterior of the protein. The missing but structurally important Ca2+ and Na+ ions were placed and aligned with PDB structure 2W26. The structure of L51a in the crystal complex structure was used as the starting point to build models for ligand L51b–L51k. For details of the system preparation, please refer to Homeyer and Gohlke’s work in the Ref. [14]. The prepared structures were used as input structures for FEW and Schrödinger FEP+ workflows after checking the correctness by visual inspection on the assignment of residue protonation states, rotamers, disulfide bond connections, ions, termini, ligand atom types and starting conformations. The apparent pKa prediction (pKaapp) from the ACD Labs/pKa DB (v.11.02, Advanced Chemistry Development, Inc., Toronto, Ontario, Canada) is based on experimental data and is widely accepted as providing quality pKa predictions. We estimated the protonated state structures of the inhibitors using the ACD Labs/pKa DB calculation algorithm [16, 17] (see Table 1), leading to significant changes from the neutral state of the inhibitors exclusively used in the original FEW paper [14]. The preferred, protonated input structures of receptor and inhibitors were used in comparisons of the FEP+ and AMBER TI predictions later.
Table 1.
Structures, apparent pKa, experimental Ki and converted binding affinities of the Factor X a inhibitors
 | ||||
|---|---|---|---|---|
| Ligand | R1 (Charged) | pKaapp (charged) | Kia | ΔGb |
| L51a |  |
7.84 | 15.9 | −10.71 |
| L51b |  |
8.41 | 1.4 | −12.15 |
| L51btc |  |
7.55 | 1.4 | −12.15 |
| L51c | 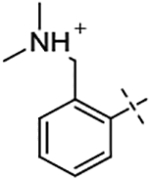 |
8.60 | 8.1 | −11.11 |
| L51d |  |
7.66 | 2255.0 | −7.75 |
| L51ed |  |
7.38 | 147.0 | −9.38 |
| L51f |  |
7.66 | 3.0 | −11.70 |
| L51g |  |
7.42 | 4.4 | −11.47 |
| L51hd |  |
6.91 | 4.1 | −11.51 |
| L51i |  |
8.92 | 690.0 | −8.46 |
| L51k |  |
8.62 | 4.9 | −11.41 |
Experimentally measured Ki (unit: nM) are taken from Ref. [18]
Free energies (unit: kcal/mol) are converted based on experimental Ki values by ΔG = −RT lnKi with T = 300 K
L51bt is the tautomer structure of L51b
Protonated structure was used as the corrected ligand structure of L51e, L51h since their pKaapp are close to 7.4
AMBER FEW TI calculations
The AMBER FEW thermodynamic integration approach was used to calculate relative binding free energies using the AMBER14 suite [19]. Nine ligand transformations based on the structural similarity score in the Ref. [14] were preserved in this work. Within the workflow, atom types of the inhibitors were automatically assigned from General Amber Force Field (GAFF) [20], atomic partial charges were prepared using the AM1-BCC approach [21, 22], and the relative binding free energies (ΔΔGbind) between two structurally similar ligands was determined by the dual topology, soft-core approach [23]. For each transformation, the alchemical space was divided into nine λ-values from 0.1 to 0.9 with Δλ = 0.1. Simulations at the endpoints (λ = 0 and λ = 1) were not conducted, as recommended for the soft-core approach in AMBER. A default of 5 ns simulation length was run in each of the nine λ windows. Both of the ff99SB and ff12SB force fields were employed to calculate Δ3ΔGbind of the original data sets, and the ff12SB were applied as the default force field. The convergence was repeatedly measured every 250 ps, and the simulation at the given λ step will be terminated once it is below the defined threshold.
| (1) |
The differences in the free energies for the complex and ligand transformation were calculated according to Eq. (1), respectively. Binding free energy was computed by numerical integration employing the calculation approaches with and without linear extrapolation of dV/dλ to the physical end states at λ = 0 and 1.
| (2) |
Since the same receptor was used, by taking the difference of these values, Eq. (2) gives the relative binding free energy. (Details of the TI setup protocol and determination of the ligand pairs for the transformation simulations are described in Ref. [14]).
Schrödinger FEP calculations
The relative binding free energies were estimated using the Desmond FEP+ module in Schrödinger Maestro Suite 2015 [24]. The OPLS2005 force field was used to describe the protein and ligand. The setup of the FEP [25] calculation was automated by the FEP+ module, in which the CM1A-BCC method was used to prepare ligand atomic partial charges [26]. Unlike the AMBER TI workflow, the Desmond FEP+ has been implemented on a graphics processing unit (GPU) platform. A FEP/REST (free energy perturbation/replica exchange with solute tempering) algorithm [27, 28] was employed to accelerate conformational sampling by effectively locally heating the binding region [28]. The ligand transformations were determined by using the FEP Mapper module based on the similarity scores. The direct transformations (no intermediate ligands involved) which contain the same ligand pairs as the TI calculations were selected for the final FEP calculations. Cycle closure calculations [29] were used for error analysis. Details of the method were described in Ref. [2].
Results and discussion
Re-examination of AMBER force fields, convergence methods and linear extrapolation
In the showcase example of Homeyer and Gohlke’s work [14], the AMBER ff99SB force field was used to conduct the TI calculations for the ligands in their neutral states using convergence method 1 (details of the convergence methods are described in below). By taking the FEW TI workflow approach, we repeated the TI calculations with the same settings and additionally carried out calculations with the newer ff12SB force field. Similar TI ΔΔG predictions were generated as the Ref. [14] using the ff99SB force field with a correlation R2 = 0.88 to the result with linear extrapolation at the endpoints (see data in Table S1, Fig. S1). Compared to the AMBER ff99SB, the ff12SB force field markedly improved the correlation of the relative binding free energy with the experimental result regardless of which convergence method was used, shown in Table 2. The ff12SB force field was thereafter used as the default.
Table 2.
Correlation R2 of AMBER TI relative binding affinity predictions to the experimental results using ff99SB and ff12SB force fields
| Approach | ΔΔGTI etp,c1 | ΔΔGTI etp,c2 | ΔΔGTI noetp,c1 | ΔΔGTI noetp,c2 |
|---|---|---|---|---|
| ff99SB | 0.29 | 0.29 | 0.35 | 0.34 |
| ff12SB | 0.41 | 0.39 | 0.42 | 0.42 |
| Ligand Correctiona | 0.63 | 0.64 | 0.71 | 0.73 |
TI calculations with linear extrapolation (etp) or without extrapolation (noetp) coupled with convergence method 1 (c1) and method 2 (c2) are listed in the table
Ligands were corrected with protonation state at pH = 7.4 (charged form) and optimal tautomerization and ff12SB force field was applied for the calculations
Two approaches were employed to check the convergence of the dV/dλ values as implemented in FEW, where method 1 evaluated the difference in the standard error of the mean dV/dλ values [23] with error limit 0.01 kcal/mol in two successive checking steps, and method 2 examined the deviation of the true mean of dV/dλ from the sample mean by using the Student’s distribution and a confidence limit of 95 % with error limit 0.2 kcal/mol. We found method 2 converged slightly more slowly than method 1. However, the differences in the uncertainties of the calculated ΔΔGbind values are trivial, and there is almost no difference in the overall correlations to the experimental result (details of the result are shown Table S1).
Consistent with the finding in the Ref. [14], the ΔΔG predictions without extrapolation at the end states using both convergence methods were markedly improved over the linear extrapolation result, which is commonly understood by the nonlinear dV/dλ curves.
Improvement of AMBER TI predictions with ligand protonation state and tautomerization correction
In drug discovery, protonation states and tautomerization are easily overlooked. By using the commonly applied apparent pKa prediction tool ACD Labs/pKa DB, of which prediction algorithm [16, 17] is based on experimental data and is widely accepted as providing quality pKa predictions, we determined the protonation states of each ligand at pH = 7.4 (data are shown in Table 1). TI predictions of the relative binding affinities of charged ligand transformations are listed in Table S2. Generally, a thermodynamically stable tautomer is favored at equilibrium. Experimentally, ligand L51b is about 11 fold more potent than L51a, resulting in a −1.45 kcal/mol experimental ΔΔG, while the calculation suggested a +1.52 kcal/mol ΔΔG. Quantum Mechanics calculations indicated the tautomer state of ligand L51b is preferred. By considering the alternative tautomer of ligand L51b (referred as ligand L51bt), we found that the predicted relative binding affinity of L51bt to L51a was significantly improved and ΔΔG was now −1.17 kcal/mol. The rank was false predicted by using L51b structure, where 2.23 kcal/mol (3.73 kcal/mol by using ff99SB) was found by using neutral state of the inhibitors, and 1.52 kcal/mol in charged state; by using the L51bt structure, the ΔΔGbind reduced to 0.16 kcal/mol in neutral state, and moved to −1.17 kcal/mol in charged state which captured the correct rank in a tolerated error.
The effect on overall correlations of AMBER TI predicted relative binding affinities are shown in Table 2, demonstrating the importance of incorporating ligand state at pH = 7.4 and tautomerization correction. After correcting the ligand structures, the correlation R2 of AMBER TI prediction was improved remarkably from 0.41 to 0.63 (up to 0.73 without linear extrapolation), and the root mean squared error (RMSE) was reduced to less than 1.0 kcal/-mol within the experimental error (shown in Fig. 1).
Fig. 1.
Correlation of AMBER TI relative binding affinity predictions with convergence method 2 and no linear extrapolation coupled to the experimental results (The left panel shows the TI calculations using ff99SB force field with original neutral ligands, and the right panel shows the TI calculations using ff12SB force field with corrected charged ligands and tautomer)
Schrödinger FEP prediction
By taking the Schrödinger FEP+ workflow using Desmond, we conducted the FEP calculations for the ligand transformations determined by the FEP Mapper tool. The uncorrected FEP-predicted relative binding affinities and cycle closure corrected energetics for the ligands in both neutral state and charged state are shown in Table S3. By fitting to the experimental results, a correlation coefficient R2 of 0.38 was found for the neutral ligand pair transformations and 0.49 for the charged ligand pairs. Interestingly, the cycle closure correction contributed no improvement to the correlation.
Comparison of Schrödinger FEP and AMBER TI workflows
By taking the same input structures, the calculation results by using Schrödinger FEP (corrected predictions) were highly correlated with the AMBER TI predictions (with linear extrapolation). They are almost equivalent with a correlation R2 = 0.80, RMSE = 0.64 kcal/mol at neutral state, and R2 = 0.96, RMSE = 0.30 kcal/mol when the charges and protonation states are corrected for all the ligands (the correlation of Amber TI and Schrödinger FEP are shown in Fig. 2).
Fig. 2.
Correlation of AMBER FEW TI prediction with Schrödinger FEP for the relative binding affinities of ligand transformations at neutral state (left panel) and charged state (right panel) (Note Both plots showed the AMBER TI result using extrapolation and convergence method 1. Similar correlations were found by using no extrapolation or convergence method 2, shown in Fig. S2)
The Schrödinger FEP and AMBER TI workflows are then comparable except for the speed: for the AMBER TI workflow, it takes approximately 1 week to perform one transformation with TI calculation on a state-of-the-art computer cluster using 64 CPU cores (16 cores/node) per λ window, but it only takes a day or less to complete one Schrödinger FEP calculation using 4 GPU cores per transformation. GPU supported AMBER TI module is in active development and is expected to be available in the AMBER16 release [30].
Conclusion
Herein, we first repeated the calculation with the same data set as used in the original FEW [14] work which led to similar correlation R2 to the experiments. Then, we carefully examined the influences of using different force fields and control parameters, and further investigated the effect of protonation and tautomerization states on the calculated ligand binding affinity. Variation of the convergence methods in AMBER FEW makes negligible difference to the correlation of the prediction to experimental data. However, linear extrapolation slightly reduced the accuracy of the predictions. As expected, the AMBER ff12SB improves the correlation R2 to the experiments from 0.29 to 0.41 (or from 0.35 to 0.42) compared to the ff99SB force field.
Compared to the published predictions based on Factor X inhibitors in their neutral state, the usage of correct protonation states boosted both AMBER TI and Schrödinger FEP, where the result R2 correlation was improved up to 0.49 in Schrödinger FEP and 0.73 in AMBER TI. Using the right tautomer state significantly reduced the prediction error, and corrected the ranking between the example inhibitors transformation (e.g. L51a to L51b).
We further benchmarked the AMBER TI in FEW with the Schrödinger FEP+. To our knowledge, this is the first performance comparison of predictions between the AMBER FEW with the Schrödinger FEP+. Although the AMBER TI calculation is relatively slow, the accuracy of both methods is almost equivalent. It proves that the AMBER TI method can be valuable for accurately determining relative binding affinity of chemically similar, pharmaceutical-like compounds.
Supplementary Material
Acknowledgments
We are grateful to Merck Research Laboratories (MRL) Postdoctoral Research Fellows Program for financial support provided by a fellowship (Y. H.). We thank the AMBER FEW developers Nadine Homeyer and Holger Gohlke for valuable help and discussions in building the workflows. We thank the High Performance Computing (HPC) support at Merck.
Abbreviations
- TI
Thermodynamic integration
- FEP
Free energy perturbation
- MM-GBSA
Molecular mechanics-generalized born surface area
- MM-PBSA
Molecular mechanics-Poisson Boltzmann surface area
- LIE
Linear interaction energy
- MCSS
Maximum common substructure search
- FEW
Free-energy workflows
- SBDD
Structure-based drug design
- MD
Molecular dynamics
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s10822-016-9920-5) contains supplementary material, which is available to authorized users.
References
- 1.Lovering F, Aevazelis C, Chang J, Dehnhardt C, Fitz L, Han S, Janz K, Lee J, Kaila N, McDonald J, Moore W (2016) Imidazotriazines: spleen tyrosine kinase (Syk) inhibitors identified by free-energy perturbation (FEP). ChemMedChem 11:217–233 [DOI] [PubMed] [Google Scholar]
- 2.Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, Lupyan D, Robinson S, Dahlgren MK, Greenwood J, Romero DL (2015) Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J Am Chem Soc 137:2695–2703 [DOI] [PubMed] [Google Scholar]
- 3.Armacost KA, Goh GB, Brooks CL III (2015) Biasing potential replica exchange multisite λ-dynamics for efficient free energy calculations. J Chem Theory Comput 11:1267–1277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jiang W, Roux B (2010) Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J Chem Theory Comput 6:2559–2565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chodera JD, Mobley DL, Shirts MR, Dixon RW, Branson K, Pande VS (2011) Alchemical free energy methods for drug discovery: progress and challenges. Curr Opin Struct Biol 21:150–160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Michel J, Essex JW (2010) Prediction of protein–ligand binding affinity by free energy simulations: assumptions pitfalls and expectations. J Comput Aided Mol Des 24:639–658 [DOI] [PubMed] [Google Scholar]
- 7.Jorgensen WL, Tirado-Rives J (2005) Molecular modeling of organic and biomolecular systems using BOSS and MCPRO. J Comput Chem 26:1689–1700 [DOI] [PubMed] [Google Scholar]
- 8.Loeffler HH, Michel J, Woods C (2015) FESetup: automating setup for alchemical free energy simulations. J Chem Inf Model 55:2485–2490 [DOI] [PubMed] [Google Scholar]
- 9.Liu S, Wu Y, Lin T, Abel R, Redmann JP, Summa CM, Jaber VR, Lim NM, Mobley DL (2013) Lead optimization mapper: automating free energy calculations for lead optimization. J Comput Aided Mol Des 27:755–770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Klimovich PV, Shirts MR, Mobley DL (2015) Guidelines for the analysis of free energy calculations. J Comput Aided Mol Des 29:397–411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Klimovich PV, Shirts MR, Mobley DL (2015) A Python tool to set up relative free energy calculations in GROMACS. J Comput Aided Mol Des 29:1007–1014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gapsys V, Michielssens S, Seeliger D, de Groot BL (2015) pmx: automated protein structure and topology generation for alchemical perturbations. J Comput Chem 36:348–354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sadiq SK, Wright D, Watson SJ, Zasada SJ, Stoica I, Coveney PV (2008) Automated molecular simulation based binding affinity calculator for ligand-bound HIV-1 proteases. J Chem Inf Model 48:1909–1919 [DOI] [PubMed] [Google Scholar]
- 14.Homeyer N, Gohlke H (2013) FEW: a workflow tool for free energy calculations of ligand binding. J Comput Chem 34:965–973 [DOI] [PubMed] [Google Scholar]
- 15.Homeyer N, Gohlke H (2015) Extension of the free energy workflow FEW towards implicit solvent/implicit membrane MM–PBSA calculations. Biochim Biophys Acta Gen Subj 1850:972–982 [DOI] [PubMed] [Google Scholar]
- 16.Liao CZ, Nicklaus MC (2009) Comparison of nine programs predicting pK(a) values of pharmaceutical substances. J Chem Inf Model 49:2801–2812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meloun M, Bordovska S (2007) Benchmarking and validating algorithms that estimate pK(a) values of drugs based on their molecular structures. Anal Bioanal Chem 389:1267–1281 [DOI] [PubMed] [Google Scholar]
- 18.Pinto DJ, Orwat MJ, Wang S, Fevig JM, Quan ML, Amparo E, Cacciola J, Rossi KA, Alexander RS, Smallwood AM, Luettgen JM (2001) Discovery of 1-[3-(Amino-methyl) phenyl]-N-[3-flu oro-2′-(methylsulfonyl)-[11′-biphenyl]-4-yl]-3-(trifluoromethyl)-1 H-pyrazole-5-carboxamide (DPC423) a highly potent selective and orally bioavailable inhibitor of blood coagulation factor Xa 1. J Med Chem 44:566–578 [DOI] [PubMed] [Google Scholar]
- 19.Case DA, Berryman JT, Betz RM, Cerutti DS, Cheatham TE III, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko A, Lee TS, LeGrand S, Li P, Luchko T, Luo R, Madej B, Merz KM, Monard G, Needham P, Nguyen H, Nguyen HT, Omelyan I, Onufriev A, Roe Roitberg A, Salomon-Ferrer R, Simmerling CL, Smith W, Swails J, Walker RC, Wang J, Wolf RM, Wu X, York DM, Kollman PA (2015) AMBER 2015. University of California, San Francisco [Google Scholar]
- 20.Wang J, Wolf R, Caldwell J, Kollamn P, Case D (2004) Development and testing of a general amber force field. J Comput Chem 25:1157–1174 [DOI] [PubMed] [Google Scholar]
- 21.Jakalian A, Bush B, Jack D, Bayly C (2000) Fast efficient generation of high-quality atomic charges AM1-BCC model: I Method. J Comput Chem 21:132–146 [DOI] [PubMed] [Google Scholar]
- 22.Jakalian A, Jack D, Bayly C (2002) Fast efficient generation of high-quality atomic charges AM1-BCC model: II parameterization and validation. J Comput Chem 23:1623–1641 [DOI] [PubMed] [Google Scholar]
- 23.Steinbrecher T, Joung I, Case DA (2011) Soft-core potentials in thermodynamic integration: comparing one and two-step transformations. J Comput Chem 32:3253–3263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Desmond Molecular Dynamics System, version 4.3, D. E. Shaw Research, New York, NY, 2015. Maestro-Desmond Interoperability Tools, version 4.3, Schrödinger, New York, NY, 2015 [Google Scholar]
- 25.Zwanzig RW (1954) High-temperature equation of state by a perturbation method I nonpolar gases. J Chem Phys 22:1420–1426 [Google Scholar]
- 26.Storer J, Giesen D, Cramer C, Truhlar D (1995) Class IV charge models: a new semiempirical approach in quantum chemistry. J Comput Aided Mol Des 9:87–110 [DOI] [PubMed] [Google Scholar]
- 27.Liu P, Kim B, Friesner RA, Berne B (2005) Replica exchange with solute tempering: a method for sampling biological systems in explicit water. J Proc Natl Acad Sci USA 102:13749–13754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang L, Berne BJ, Friesner RA (2012) On achieving high accuracy and reliability in the calculation of relative protein–ligand binding affinities. Proc Natl Acad Sci USA 109:1937–1942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang L, Lin T, Abel R, Schrödinger LLc (2013) Cycle closure estimation of relative binding affinities and errors. US Patent Application 13/840039
- 30.Case DA, Betz RM, Cerutti DS, Cheatham TE III, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko A, Lee TS, LeGrand S, Li P, Lin C, Luchko T, Luo R, Madej B, Mermelstein D, Merz KM, Monard G, Nguyen H, Nguyen HT, Omelyan I, Onufriev A, Roe DR, Roitberg A, Sagui C, Simmerling CL, Botello-Smith WM, Swails J, Walker RC, Wang J, Wolf RM, Wu X, Xiao L, Kollman PA (2016) AMBER 2016. University of California, San Francisco [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




