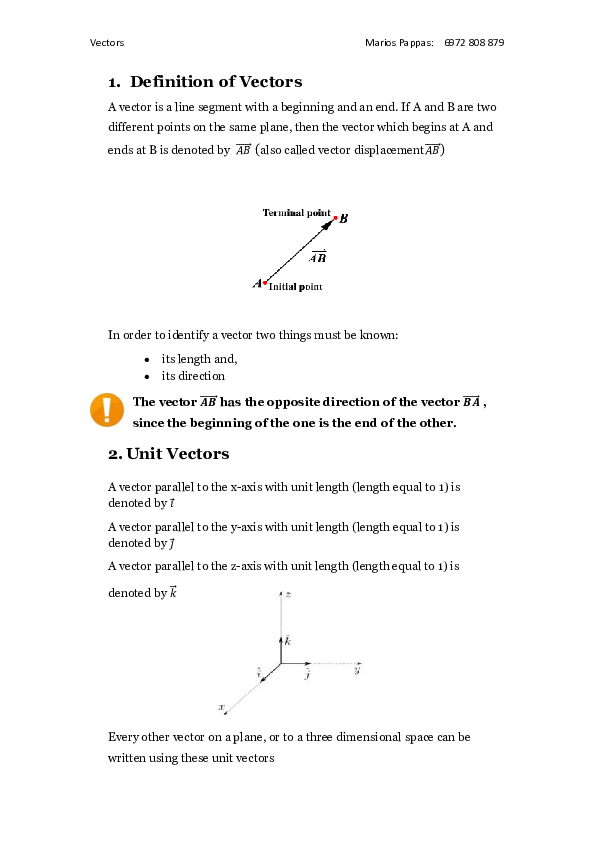
Vectors Marios Pappas: 6972 808 879 1. Definition of Vectors A vector is a line segment with a beginning and an end. If A and B are two different points on the same plane, then the vector which begins at A and ends at B is denoted by (also called vector displacement ) In order to identify a vector two things must be known:   its length and, its direction The vector has the opposite direction of the vector since the beginning of the one is the end of the other. 2. Unit Vectors A vector parallel to the x-axis with unit length (length equal to 1) is denoted by A vector parallel to the y-axis with unit length (length equal to 1) is denoted by A vector parallel to the z-axis with unit length (length equal to 1) is denoted by Every other vector on a plane, or to a three dimensional space can be written using these unit vectors , Vectors Marios Pappas: 6972 808 879 You may see unit vectors called as base vectors 3. Scalar Multiplication If a vector is multiplied by a real number b, then a vector is produced which has length of units and the same direction with if b> 0 or the opposite direction of if b< 0. If b=0 then the product is the zero vector 0, with no length or direction. 4. Vector Addition In order to add two vectors and , we consider the vector the same beginning with and the end of at the end of through a parallelogram. + which has when the beginning of is put Vectors Marios Pappas: 6972 808 879 5. Cartesian Notation In order to identify a vector and to perform vector operations, we use the Cartesian notation. Then the vector is written in column vector form. Each number in each row of the column represents the x, y or z component of the vector. For example the vector = 3 + 2 − 5 could be represented as 3 = 2 −5 Performing operations with vectors is now an easy task. For the scalar multiplication we have to multiply each component with the considered real number, and for the vector addition we have to perform addition by component. Example: 2 = 1 and 3 Consider two given vectors = −2 1 4 Then, 10 5∙2 5 = 5∙1 = 5 15 5∙3 + 2 + (−2) 0 = = 2 1+1 7 4+3 is point A(xα,yα,zα) and the end is point If the beginning of the vector B(xb,yb,zb), then and = (xb– xα,yb - yα, zb - zα) Example:Consider the vectors A = (2,1,-7) and B = (0,1,1). = Then = 0−2 −2 1−1 = 0 1 − (−7) 8 2−0 1−0 = −7 − 1 As you can see 2 0 −8 = (−1) ∙ Vectors Marios Pappas: 6972 808 879 If two vectors and are parallel, we can write that =t for some scalar t. 6. Position Vector Every point P on a plane (or on the 3 dimensional space) can be where O(0,0) (or O(0,0,0) for the 3 represented by its position vector dimensional). ℎ So if P= ℎ � −0 −0 = −0 = 7. Angles If we need to find an angle between two lines then we may consider the vectors lines. and and use them to find the cosine of the angle between the 1 If = 2 1 and = 3 2 3 then �1∙ cosθ= 1+ 2 ∙ 2 + 3 ∙ 3 ∙ The expression in the numerator called inner product or dot product of by ∙ If ∙ =0 then the vectors and ∙ ∙ + and + ∙ is and is notated are perpendicular 8. Distances 1 By using Pythagorean Theorem for a vector distance from the origin to the end of the vector is This value is called the magnitude of = we can find the 2 3 2 1 + and is denoted by 2 . 2 + 3 2. Vectors Marios Pappas: 6972 808 879 The distance between points with position vectors Two vectors and may not be equal. and is − . may have the same magnitudes, but they 9. Vector Product For every two vectors a, b another product can be defined which gives a new vector as a result: �1 � If α = 2 and b = �3 �2 α� = �3 1 − �3 1 − �1 2 − �2 3 1 2 then 3 2 3 1 α� is called the vector product (or cross product) of α and b. The vector product of αand b, denoted by α� has magnitude � ���, where θis the angle between αand b. The direction of α� is perpendicular to both αand b as shown. Algebraic properties of the vector product �� = −��� Vectors Marios Pappas: 6972 808 879 �� � = (�� ) + = �� + (�� ) �� If vectors α and b are parallel then �� =0. If vectors α and b are perpendicular then �� = � . Area of a triangle formed by vectors By using the vector product, the area of the triangle whose two sides are αand b is equal to 10. �� . Vector equation of a line. The expression r = �+ is a vector equation of a line. The vector is the direction vector of the line and � is the position vector of one point of the line. Example: Find the vector equation of the line passing through points A(3,2) and B(5,3). The vector equation of the line is �= = So, = 5 3 = �+ 2 5−3 = 1 3−2 = 2 5 +� 1 3 The angle between two lines is equal to the angle between their direction vectors. Two lines with direction vectors 1 and 2 are: Vectors   Marios Pappas: 6972 808 879 Parallel if 1 = Perpendicular if 11. 2 1 ∙ 2 =0 Cartesian equation of a line 1 Consider the equation of the line = 2 + 3 Assuming that r= , we write 1 = 2 + 3 Then x=1+3 3 5 . −5 3 5 . −5 y=2+5 z=3-5 If we solve each equation for : = −1 = −2 = hence, 12. −1 3 = −2 5 = 3− 5 3 5 3− 5 represents the Cartesian equation of the line. Intersection of two lines Example: Find the point of intersection of the lines 1: = 5 2 + −1 1 −2 −3 and 2: = 2 0 + 4 The coefficients must me equal: x = 5+ = 2+ y = 2-2 = 2 z = -1-3 = 4Solving the system of these 3 equations we can find the values of and Hence, = -1 and =2 1 2 −1 Vectors Marios Pappas: 6972 808 879 Now substitute into the equation of one of the two lines: x = 5-1 = 4 y = 2+2 = 4 z = -1+3 =2