Discrete Mathematics | Hasse Diagrams

Last Updated : 09 Aug, 2024
Comments
Improve
Suggest changes
Like Article
Like
Save
Share
Report
News Follow

Hasse Diagram

A Hasse diagram is a graphical representation of the relation of elements of a partially ordered set (poset) with an implied upward orientation. A point is drawn for each element of the partially ordered set (poset) and joined with the line segment according to the following rules: 
 

  • If p<q in the poset, then the point corresponding to p appears lower in the drawing than the point corresponding to q.
  • The two points p and q will be joined by line segment if p is related to q.


To draw a Hasse diagram, the provided set must be a poset. 
A poset or partially ordered set A is a pair, ( B, [Tex]\leq          [/Tex]) of a set B whose elements are called the vertices of A and obeys following rules: 
 

  1. Reflexivity → p [Tex]\leq          [/Tex]p [Tex]\forall          [/Tex]p [Tex]\in          [/Tex]B
  2. Anti-symmetric → p [Tex]\leq          [/Tex]q and q [Tex]\leq          [/Tex]p if p=q
  3. Transitivity → if p [Tex]\leq          [/Tex]q and q [Tex]\leq          [/Tex]r then p [Tex]\leq          [/Tex]r


Example-1: Draw Hasse diagram for ({3, 4, 12, 24, 48, 72}, /) 

Explanation – According to above given question first, we have to find the poset for the divisibility. 
Let the set is A. 
A={(3 [Tex]\prec          [/Tex]12), (3 [Tex]\prec          [/Tex]24), (3 [Tex]\prec          [/Tex]48), (3 [Tex]\prec          [/Tex]72), (4 [Tex]\prec          [/Tex]12), (4 [Tex]\prec          [/Tex]24), (4 [Tex]\prec          [/Tex]48), (4 [Tex]\prec          [/Tex]72), (12 [Tex]\prec          [/Tex]24), (12 [Tex]\prec          [/Tex]48), (12 [Tex]\prec          [/Tex]72), (24 [Tex]\prec          [/Tex]48), (24 [Tex]\prec          [/Tex]72)} 
So, now the Hasse diagram will be: 
 

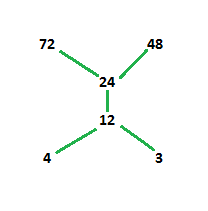
example 1


In above diagram, 3 and 4 are at same level because they are not related to each other and they are smaller than other elements in the set. The next succeeding element for 3 and 4 is 12 i.e, 12 is divisible by both 3 and 4. Then 24 is divisible by 3, 4 and 12. Hence, it is placed above 12. 24 divides both 48 and 72 but 48 does not divide 72. Hence 48 and 72 are not joined. 
We can see transitivity in our diagram as the level is increasing. 

Example-2: Draw Hasse diagram for (D[Tex]_{12}          [/Tex], /) 

Explanation –

Here, D[Tex]_{12}          [/Tex]means set of positive integers divisors of 12. 
So, D[Tex]_{12}          [/Tex]={1, 2, 3, 4, 6, 12} 
poset A = {(1 [Tex]\prec          [/Tex]2), (1 [Tex]\prec          [/Tex]3), (1 [Tex]\prec          [/Tex]4), (1 [Tex]\prec          [/Tex]6), (1 
[Tex]\prec          [/Tex]12), (2 [Tex]\prec          [/Tex]4), (2 [Tex]\prec          [/Tex]6), (2 [Tex]\prec          [/Tex]12), (3 [Tex]\prec          [/Tex]6), (3 [Tex]\prec          [/Tex]12), (4 [Tex]\prec          [/Tex]12), (6 [Tex]\prec          [/Tex]12)} 
So, now the Hasse diagram will be- 
 

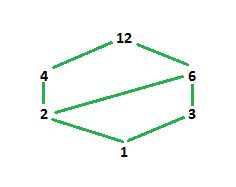
example 2


In above diagram, 1 is the only element that divides all other elements and smallest. Hence, it is placed at the bottom. Then the elements in our set are 2 and 3 which do not divide each other hence they are placed at same level separately but divisible by 1 (both joined by 1). 4 is divisible by 1 and 2 while 6 is divisible by 1, 2 and 3 hence, 4 is joined by 2 and 6 is joined by 2 and 3. 12 is divisible by all the elements hence, joined by 4 and 6 not by all elements because we have already joined 4 and 6 with smaller elements accordingly. 

For regular Hasse Diagram: 
 

  • Maximal element is an element of a POSET which is not less than any other element of the POSET. Or we can say that it is an element which is not related to any other element. Top elements of the Hasse Diagram.
  • Example- In the diagram above, we can say that 4,2,3,6,1 are related to 12 (ordered by division e.g. (4,/) ) but 12 is not related to any other. (As Hasse Diagram is upward directional).
  • Minimal element is an element of a POSET which is not greater than any other element of the POSET. Or we can say that no other element is related to this element. Bottom elements of the Hasse Diagram.
  • Example- In the diagram above, we can say that 1 is related to 2,3,4,6,12 (ordered by division e.g. (4,/) ) but no element is related to 1. (As Hasse Diagram is upward directional).
  • Greatest element (if it exists) is the element succeeding all other elements.
  • Least element is the element that precedes all other elements.



Note – Greatest and Least element in Hasse diagram are only one. 

In Example-1, 
Maximal elements are 48 and 72 since they are succeeding all the elements. 
Minimal elements are 3 and 4 since they are preceding all the elements. 
Greatest element does not exist since there is no any one element that succeeds all the elements. 
Least element does not exist since there is no any one element that precedes all the elements. 

In Example-2, 
Maximal and Greatest element is 12 and Minimal and Least element is 1.

NOTE: An element can be both maximal and minimal 

Example-

Here a,b,c are maximal as well as minimal.


Solved Examples:

Example 1:

Consider the poset ((P, \leq)) where (P = {1, 2, 3, 4, 6, 12}) and the relation (\leq) is divisibility.

Elements: 1, 2, 3, 4, 6, 12

Order Relations: 1 divides all, 2 divides 4 and 6, 3 divides 6, 4 divides 12, 6 divides 12.[Tex]Example 1: Consider the poset ((P, \leq)) where (P = {1, 2, 3, 4, 6, 12}) and the relation (\leq) is divisibility. Elements: 1, 2, 3, 4, 6, 12 Order Relations: 1 divides all, 2 divides 4 and 6, 3 divides 6, 4 divides 12, 6 divides 12.[/Tex]

12 / \ 6 4 | \ / 3 2 \ / 1


Example 2:


[Tex]Consider the poset ((P, \leq)) where (P = {a, b, c, d}) and the relation (\leq) is defined as (a \leq b), (a \leq c), (b \leq d), (c \leq d). Elements: a, b, c, d Order Relations: (a \leq b), (a \leq c), (b \leq d), (c \leq d).[/Tex][Tex]Consider the poset ((P, \leq)) where (P = {a, b, c, d}) and the relation (\leq) is defined as (a \leq b), (a \leq c), (b \leq d), (c \leq d). Elements: a, b, c, d Order Relations: (a \leq b), (a \leq c), (b \leq d), (c \leq d).[/Tex]

d / \ b c \ / a

Practice Problems

Problem [Tex]1:Given the set (P = {1, 2, 4, 8}) with (\leq) being divisibility, draw the Hasse diagram.[/Tex]

Problem 2: [Tex]Given the set (P = {a, b, c, d, e}) with the relations (a \leq b), (a \leq c), (b \leq d), (c \leq d), (d \leq e), draw the Hasse diagram.[/Tex]

Problem 3: [Tex]Given the set (P = {1, 3, 9, 27}) with (\leq) being divisibility, draw the Hasse diagram[/Tex].

Problem 4: [Tex]Given the set (P = {2, 5, 10, 20}) with (\leq) being divisibility, draw the Hasse diagram[/Tex]

Problem [Tex]5:Given the set (P = {a, b, c, d, e}) with the relations (a \leq c), (b \leq c), (c \leq d), (d \leq e), draw the Hasse diagram.[/Tex]

Problem 6:[Tex]Given the set (P = {x, y, z, w}) with the relations (x \leq y), (y \leq z), (z \leq w), draw the Hasse diagram.[/Tex]

Problem 7:[Tex]Given the set (P = {m, n, o, p, q}) with the relations (m \leq n), (m \leq o), (n \leq p), (o \leq p), (p \leq q), draw the Hasse diagram.[/Tex]

Problem 8:[Tex]Given the set (P = {4, 8, 16, 32}) with (\leq) being divisibility, draw the Hasse diagram.[/Tex]

Problem [Tex]9:Given the set (P = {r, s, t, u, v}) with the relations (r \leq s), (s \leq t), (t \leq u), (u \leq v), draw the Hasse diagram.[/Tex]

Problem 10:[Tex]Given the set (P = {1, 2, 5, 10}) with (\leq) being divisibility, draw the Hasse diagram.[/Tex]

Interlinking of Related Articles:

Conclusion

Hasse diagrams are an invaluable tool in discrete mathematics, providing a clear and concise way to visualize the structure of partially ordered sets (posets). By representing the elements and their order relations without redundancy, Hasse diagrams make it easier to analyze and understand complex relationships within a set. Their applications extend to various fields, including lattice theory, graph theory, and beyond. Whether you’re a student or a professional, mastering the construction and interpretation of Hasse diagrams can enhance your ability to work with hierarchical data and posets. With practice and the right tools, you can effectively utilize Hasse diagrams to simplify and solve problems in discrete mathematics.

FAQs on Hasse Diagrams

What is a Hasse diagram?

A Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set (poset) by displaying its transitive reduction. It shows the order relations between elements without redundant edges.

How is a Hasse diagram constructed?

To construct a Hasse diagram:

1. List the elements of the poset.

2. Determine the ordering relations between the elements.

3. Draw the elements as points in a plane.

4. Connect the points with edges to represent the order relations, ensuring transitive reduction (i.e., if \(a \leq b\) and \(b \leq c\), do not draw a direct line from \(a\) to \(c\)).

What is a poset in the context of Hasse diagrams?

A poset, or partially ordered set, is a set equipped with a partial order relation. In a poset, not every pair of elements needs to be comparable, but the order relation must be reflexive, antisymmetric, and transitive.

What does transitive reduction mean?

Transitive reduction of a relation means removing all redundant edges while maintaining the same reachability between elements. In other words, if \(a \leq b\) and \(b \leq c\), the direct relation \(a \leq c\) is implied and thus not shown in the Hasse diagram.

Can Hasse diagrams be used for infinite sets?

Hasse diagrams are typically used for finite sets because they provide a clear visual representation. For infinite sets, the diagrams can become unwieldy and lose their effectiveness.

How do you identify elements and order relations in a poset?

Elements are the individual items in the set, and order relations define how these elements relate to one another according to the partial order. For example, in a poset of divisibility, if an element \(a\) divides element \(b\), there is an order relation \(a \leq b\).

What are some common applications of Hasse diagrams?

Hasse diagrams are used in various fields of mathematics, including lattice theory, order theory, and graph theory. They help in visualizing the structure of posets, analyzing hierarchical structures, and simplifying complex relationships.

What is the difference between a Hasse diagram and a directed graph?

While both Hasse diagrams and directed graphs (digraphs) represent relations between elements, Hasse diagrams specifically represent posets with transitive reduction. Digraphs can represent any directed relationships, including those that are not transitive reductions.

How does a Hasse diagram help in understanding the structure of a poset?

Hasse diagrams provide a visual representation of the hierarchical structure of a poset, making it easier to see how elements are related. They simplify the analysis of order relations by removing redundant connections.

What are some tips for drawing a Hasse diagram?

Start by listing the elements and determining the order relations. – Arrange elements in levels, with lower elements at the bottom and higher elements at the top. – Draw edges to represent direct order relations, ensuring no transitive edges are included. – Use vertical lines or arrows to maintain clarity and avoid crossing edges.

Are there any tools available for drawing Hasse diagrams?

Yes, there are several software tools and online platforms that can help in drawing Hasse diagrams, such as graph drawing software (e.g., Graphviz), mathematical tools like Mathematica, and specialized diagramming tools.

What is the significance of the Hasse diagram’s name?

The Hasse diagram is named after the German mathematician Helmut Hasse, who made significant contributions to algebra and number theory. His work in posets led to the development of these diagrams for visualizing order relations.



D
Deepanshi_Mittal
News
Improve
Previous Article
Mathematics | Introduction to Proofs
Next Article
Pigeonhole Principle

Similar Reads

Discrete Mathematics | Types of Recurrence Relations - Set 2
Prerequisite - Solving Recurrences, Different types of recurrence relations and their solutions, Practice Set for Recurrence Relations The sequence which is defined by indicating a relation connecting its general term an with an-1, an-2, etc is called a recurrence relation for the sequence. Types of recurrence relations First order Recurrence relat
4 min read
Elementary Matrices | Discrete Mathematics
Prerequisite : Knowledge of Matrices &amp; Identity Matrix Introduction :A matrix is a collection of numbers arranged in a row-by-row and column-by-column arrangement. The elements of a matrix must be enclosed in parenthesis or brackets.Example - The 3 * 3 matrix means a matrix with 3 rows &amp; 3 columns with a total of 9 elements. (3*3 = 9) Ident
3 min read
Discrete Mathematics - GATE CSE Previous Year Questions
Solving GATE Previous Year's Questions (PYQs) not only clears the concepts but also helps to gain flexibility, speed, accuracy, and understanding of the level of questions generally asked in the GATE exam, and that eventually helps you to gain good marks in the examination. Previous Year Questions help a candidate practice and revise for GATE, whic
4 min read
Real-Life Applications of Discrete Mathematics
Discrete mathematics is a branch of mathematics that deals with objects that can assume only distinct, separated values, in contrast to continuous mathematics, which deals with objects that can vary smoothly. Discrete mathematics can be used in many fields of mathematics, from computer science to telecommunications, operations research to cryptogra
6 min read
Number Theory in Discrete Mathematics
Discrete mathematics deals with counting individual items, such as whole numbers, rather than continuous quantities like real numbers. Number theory, a major component of discrete math, delves into the properties and behaviors of integers, especially natural numbers and occasionally all integers. Understanding number theory is crucial in comprehend
5 min read
Functions in Discrete Mathematics
Functions are an important part of discrete mathematics. This article is all about functions, their types, and other details of functions. A function assigns exactly one element of a set to each element of the other set. Functions are the rules that assign one input to one output. The function can be represented as f: A ⇢ B. A is called the domain
9 min read
Boolean Ring in Discrete Mathematics
Discrete mathematics is one of the subfields of mathematics that deals with discrete and separate elements using algebra and arithmetic. It is considered to be one of the fundamental branches of computer science and includes the studies of combinatorics, graphs, and logic. One of those concepts is the Boolean ring which is used in different practic
7 min read
Discrete Mathematics | Representing Relations
Prerequisite - Introduction and types of Relations Relations are represented using ordered pairs, matrix and digraphs: Ordered Pairs - In this set of ordered pairs of x and y are used to represent relation. In this corresponding values of x and y are represented using parenthesis. Example: {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25)}This represent sq
2 min read
Types of Sets in Discrete Mathematics
A set in discrete mathematics is a collection of distinct objects, considered as an object in its own right. Sets are fundamental objects in mathematics, used to define various concepts and structures. In this article, we will discuss Types of Sets in Discrete Structure or Discrete Mathematics. Also, we will cover the examples. Let's discuss one by
13 min read
Peano Axioms | Number System | Discrete Mathematics
The set of natural numbers is axiomatically defined below. G. Peano, an Italian mathematician, and J. W. R. Dedekind, a German mathematician, are credited with these axioms. These axioms aim to prove the existence of one natural number before defining a function to create the remaining natural numbers, known as the successor function. Peano AxiomsA
12 min read
Types of Proofs - Predicate Logic | Discrete Mathematics
The most basic form of logic is propositional logic. Propositions, which have no variables, are the only assertions that are considered. Because there are no variables in propositions, they are either always true or always false.Example - P: 2 + 4 = 5. (Always False) is a proposition.Q: y * 0 = 0. (Always true) is a proposition.The majority of math
14 min read
Principal Ideal Domain (P.I.D.) | Discrete Mathematics
Algebraic Structure: A non-empty set G equipped with 1 or more binary operations is called an algebraic structure.Example - (N,+) where N is a set of natural numbers and(R, *) R is a set of real numbers. Here ' * ' specifies a multiplication operation.RING : An algebraic structure that sets the processing of two binary operations simultaneously is
11 min read
Prime Numbers in Discrete Mathematics
Prime numbers are the building blocks of integers, playing a crucial role in number theory and discrete mathematics. A prime number is defined as any integer greater than 1 that has no positive divisors other than 1 and itself. Understanding prime numbers is fundamental to various mathematical concepts and applications, including cryptography, codi
9 min read
Discrete Mathematics - Applications of Propositional Logic
A proposition is an assertion, statement, or declarative sentence that can either be true or false but not both. For example, the sentence "Ram went to school." can either be true or false, but the case of both happening is not possible. So we can say, the sentence "Ram went to school." is a proposition. But, the sentence "N is greater than 100" is
11 min read
Hypergraph Representation | Discrete Mathematics
A hypergraph is a graph in which hyperedges (generalized edges) can connect to a subset of vertices/nodes rather than two vertices/nodes.The edges (also known as hyperedges) of a hypergraph are arbitrary nonempty sets of vertices. A k-hypergraph has all such hyperedges connecting exactly k vertices; a normal graph is thus a 2-hypergraph (as one edg
7 min read
PDNF and PCNF in Discrete Mathematics
PDNF (Principal Disjunctive Normal Form)It stands for Principal Disjunctive Normal Form. It refers to the Sum of Products, i.e., SOP. For eg. : If P, Q, and R are the variables then (P. Q'. R) + (P' . Q . R) + (P . Q . R') is an example of an expression in PDNF. Here '+' i.e. sum is the main operator. You might be confused about whether there exist
4 min read
Arguments in Discrete Mathematics
Introduction to Arguments in Discrete MathematicsIn discrete mathematics, an argument refers to a sequence of statements or propositions intended to determine the validity of a particular conclusion. The study of arguments in this context is crucial because it forms the basis for logical reasoning, which is essential in areas like computer science,
10 min read
Four Color Theorem and Kuratowski’s Theorem in Discrete Mathematics
The Four Color Theorem and Kuratowski's Theorem are two fundamental results in discrete mathematics, specifically in the field of graph theory. Both theorems address the properties of planar graphs but from different perspectives. In this article, we will understand about Four Color Theorem and Kuratowski’s Theorem in Discrete Mathematics, their de
14 min read
Weak Entity Set in ER diagrams
An entity type should have a key attribute which uniquely identifies each entity in the entity set, but there exists some entity type for which key attribute can’t be defined. These are called Weak Entity type. The entity sets which do not have sufficient attributes to form a primary key are known as weak entity sets and the entity sets which have
2 min read
Recursive Relationships in ER diagrams
Prerequisite - ER Model A relationship between two entities of a similar entity type is called a recursive relationship. Here the same entity type participates more than once in a relationship type with a different role for each instance. In other words, a relationship has always been between occurrences in two different entities. However, the same
3 min read
Applications of Venn Diagrams in Real Life
Applications of Venn Diagrams: Venn diagrams are popularly used in our daily life for visual representation, the Venn diagrams are used to describe how various sets overlap one another. Venn diagram uses circles for a particular group of elements and when these circles overlap each other then it means those elements have one or more common properti
9 min read
What is Mapping Cardinalities in ER Diagrams
In a Database Management System (DBMS), mapping cardinalities explains how entities (tables) in a database schema relate to one another. They provide the number of instances of one entity that can be linked to the number of instances of another entity via a certain kind of relationship, such as many-to-many, one-to-one, one-to-many, or one-to-many.
6 min read
Difference Between Discrete and Continuous Variable
In statistics, variables play a crucial role in understanding and analyzing data. Two fundamental types of variables are discrete and continuous variables. Discrete variables have distinct, separate values with gaps between them, while continuous variables have an unbroken sequence of values. In this article, we will learn about continuous variable
5 min read
Difference between Continuous and Discrete Uniform Distribution
Continuous and discrete uniform distributions are two types of probability distributions. A continuous uniform distribution has an interval of equally likely values. Instead, a discrete uniform distribution applies to a finite set of outcomes with equal probabilities. Understanding the difference between continuous and discrete uniform distribution
5 min read
Discrete Maths | Generating Functions-Introduction and Prerequisites
Discrete Maths | Generating Functions-Introduction and PrerequisitesPrerequisite - Combinatorics Basics, Generalized PnC Set 1, Set 2 Definition: Generating functions are used to represent sequences efficiently by coding the terms of a sequence as coefficients of powers of a variable (say) [Tex]\big x [/Tex]in a formal power series. Now with the fo
5 min read
Discrete Random Variable
Discrete Random Variables are an essential concept in probability theory and statistics. Discrete Random Variables play a crucial role in modelling real-world phenomena, from the number of customers who visit a store each day to the number of defective items in a production line. Understanding discrete random variables is essential for making infor
15 min read
Discrete Probability Distribution
Discrete probability distribution counts occurrences with finite outcomes. The common examples of discrete probability distribution include Bernoulli, Binomial and Poisson distributions. In this article we will explore discrete probability distribution along with discrete probability distribution definition, discrete probability distribution condit
7 min read
What are the two Requirements for a Discrete Probability Distribution
The two requirements for a discrete probability distribution are: Each probability P(X = x) must be between 0 and 1, inclusive.The sum of the probabilities for all possible outcomes must equal 1.Let's discuss these two requirements in detail. Non-Negative ProbabilitiesThe probability of each possible outcome must be non-negative. In other words, fo
3 min read
Approximations for Discrete Distributions
Approximations for discrete distributions are essential tools in the statistics and probability theory that help simplify complex problems involving the discrete random variables. This article aims to provide the detailed overview of these approximations including their relevance, applications and methods. Table of Content What are Discrete Distrib
6 min read
Mathematics | Probability Distributions Set 2 (Exponential Distribution)
The previous article covered the basics of Probability Distributions and talked about the Uniform Probability Distribution. This article covers the Exponential Probability Distribution which is also a Continuous distribution just like Uniform Distribution. Introduction - Suppose we are posed with the question- How much time do we need to wait befor
5 min read
Article Tags :