Deep learning modelling techniques: current progress, applications, advantages, and challenges

Abstract

Deep learning (DL) is revolutionizing evidence-based decision-making techniques that can be applied across various sectors. Specifically, it possesses the ability to utilize two or more levels of non-linear feature transformation of the given data via representation learning in order to overcome limitations posed by large datasets. As a multidisciplinary field that is still in its nascent phase, articles that survey DL architectures encompassing the full scope of the field are rather limited. Thus, this paper comprehensively reviews the state-of-art DL modelling techniques and provides insights into their advantages and challenges. It was found that many of the models exhibit a highly domain-specific efficiency and could be trained by two or more methods. However, training DL models can be very time-consuming, expensive, and requires huge samples for better accuracy. Since DL is also susceptible to deception and misclassification and tends to get stuck on local minima, improved optimization of parameters is required to create more robust models. Regardless, DL has already been leading to groundbreaking results in the healthcare, education, security, commercial, industrial, as well as government sectors. Some models, like the convolutional neural network (CNN), generative adversarial networks (GAN), recurrent neural network (RNN), recursive neural networks, and autoencoders, are frequently used, while the potential of other models remains widely unexplored. Pertinently, hybrid conventional DL architectures have the capacity to overcome the challenges experienced by conventional models. Considering that capsule architectures may dominate future DL models, this work aimed to compile information for stakeholders involved in the development and use of DL models in the contemporary world.

1 Introduction

Developing machines with the ability to ‘think’ has been a long-running aspiration of inventors throughout history. The popular idea of replicating intelligent human behavior arranged as processes in machines (Dick 2019) has fueled researchers’ imaginations. In the present time, artificial intelligence (AI) is a thriving and rapidly changing field with various applications in society and economics, such as understanding speech or images, textual analysis, and in supporting an actively growing research body (Lu et al. 2018). Machine learning (ML), a part of AI, is a multidisciplinary field spanning computer science, statistics, and data science that addresses the need for computers to improve automatically through experience and by the use of data (Jordan and Mitchell 2015). ML is advancing evidence-based decision-making in the fields of healthcare, education, national security, finance, economics, manufacturing, and marketing (Jordan and Mitchell, 2015), specifically by implementing various approaches to teach computers to achieve tasks. However, conventional ML techniques cannot efficiently process raw data and require mindful engineering and great expertise (Lecun et al. 2015). In the real world, every piece of data may be influenced by different factors of variations, thus requiring humans to factor in those variations and decide whether to incorporate them or not. Overcoming such flaws, deep learning (DL) has recently emerged as a promising approach in ML (Lecun et al. 2015), currently dominating the majority of the works in the field of ML (Alpaydin 2020).

While it may appear as a seemingly new concept, the idea of DL can be traced back to the 1940s and subsequently underwent roughly three waves of development with the most recent current revival beginning in 2006 (Goodfellow et al. 2016). During the first wave between 1940 and 1960, DL was known as cybernetics, then it gained popularity again in the 1980s-1990s as connectionism. Fundamental methods such as radial basis function networks and multilayer perceptrons were employed in 2014 to solve the problem of designing mobile adaptive tracking controllers (Tzafestas 2014). These two neural networks were found suitable for decision-making and control. Later, Sengupta et al. (Sengupta et al. 2020) pointed out a few reasons why DL rose to prominence in the twenty-first century, including the surge of “big data” with quality labels, improvements in regularization techniques, development of near-perfect optimization algorithms, creation of niche software platforms that can enable the integration of architectures, and advancements in parallel computing power and multi-core, multi-threaded execution. In fact, big data became a huge issue for conventional ML algorithms along with the increasing size of the network, whereby the performance of old algorithms either became overloaded or deteriorated (Khamparia and Singh 2019). The enhanced performance of DL can be attributed to its ability to utilize two or more levels of non-linear feature transformation of the given data (Zeiler and Fergus 2014).

Deep learning allows computational models with multiple layers to gradually extract higher-level features from the raw input (Alpaydin 2020; Deng and Yu 2014). The “deep” in DL, therefore, denotes a high credit assignment path (CAP) depth, which has been assigned a value of 2 by most researchers (Sugiyama 2019; Telikani et al. 2021; Kashyap et al. 2021; Mousavi and Gandomi 2021; Tahmassebi et al. 2018a, b, 2019, 2020; Jayaraman et al. 2020; Kumar et al. 2019). Deep learning enables computers to learn complex concepts by forming them out of simple ones. Goodfellow et al. (2016) adequately explained that, “Deep learning is a particular kind of machine learning that achieves great power and flexibility by learning to represent the world as a nested hierarchy of concepts, with each concept defined in relation to simpler concepts, and more abstract representations computed in terms of less abstract ones” (Goodfellow et al. 2016). DL is primarily based on artificial neural networks, a type of computing system roughly mimicking the biological neural networks of animal brains (Chen et al. 2019), and may employ supervised, unsupervised, or semi-supervised representation learning (Bengio et al. 2013; Lecun et al. 2015; Schmidhuber 2015). Representation learning, also known as feature learning, sets DL apart from other techniques in ML. Unlike manual feature engineering, feature learning enables computers to spontaneously find the representations required for the classifications from raw data (Bengio et al. 2013). DL, therefore, relies on very little hand-tuning and has the ability to analyze the rapidly increasing computations and data. The requirement for manual engineering is only restricted to operations, such as altering the numbers and sizes of layers, to yield different degrees of abstraction (Bengio et al. 2013; Lecun et al. 2015).

The applications of DL span various disciplines and sectors. To begin with, DL has exhibited remarkable performance in image recognition (Carrio et al. 2017; Krizhevsky and Hinton 2017; Lecun et al. 2015; Szegedy et al. 2015; Tompson et al. 2014; Wei et al. 2019), displayed potential in image restoration (Schmidt 2014), and demonstrated groundbreaking results in speech recognition (Cireşan et al. 2012; Deoras et al. 2011; Hinton et al. 2012; Lecun et al. 2015; Sainath et al. 2013). It is currently used in the speech recognition systems of major day-to-day products (Case et al. 2014; Deng and Yu 2014; Lemley et al. 2017) as well as in the operation of unmanned vehicles (Carrio et al. 2017). The area of language processing has also been harnessing the benefits of DL (Deng and Yu 2014), in which DL contributes to natural language understanding and translation (Collobert et al. 2011; Mesnil et al. 2015; Sutskever et al. 2014), query response (Bordes et al. 2014), sentiment analysis, text classification, information recovery (Huang et al. 2013; Shen et al. 2014), and writing style recognition (Brocardo et al. 2017), just to name a few. DL has also been revolutionizing the health sector (Miotto et al. 2018), particularly yielding far-reaching implications for drug discovery and design and in effectively predicting interactions of potential drugs with molecules of interest (Ma et al. 2015). DL’s ability to acquire end-to-end learning models from complex, unstructured, diverse, and poorly annotated data has also led to advancements in biomedical research (Collobert et al. 2011; Naylor 2018; Ravì et al. 2017). With its high image recognition skills, DL has been applied in clinical imaging, such as neuroimaging (Sui et al. 2020), and has shown great promise in the identification and detection of lesions, cancer cells, and different organs, as well as in image enhancement (Cao et al. 2019; Litjens et al. 2017; Wieslander et al. 2017). Bioinformatics has also applied DL for predicting gene ontology annotations, understanding the functions of different genes (Chicco et al. 2014), and most importantly for anticipating how mutations in non-coding DNA affect gene expressions and susceptibility to diseases (Leung et al. 2014; Xiong et al. 2016).

DL’s applications range far beyond science. For example, the military has taken advantage of the highly efficient image and object recognition ability of DL for various operations (Mendis et al. 2016; Yang et al. 2018). Businesses have applied DL for improving their customer relationship management, where it allows for the estimation of the customer lifetime value that would result from possible direct marketing activities (Tkachenko 2015). The recommendation systems in various commercial products utilize DL to understand and predict user preferences (Da’u and Salim 2020; Feng et al. 2019; Oord et al. 2013). Similarly, it has been also used in targeting an appropriate audience for mobile advertisements (De et al. 2017). Furthermore, DL utilizes both supervised and unsupervised learning in financial fraud detection and anti-money laundering by identifying anomalies and abnormal money transactions (Paula et al. 2016). While DL has been helping to advance several fields of research, society, and the economy, it can also be exploited for malicious attempts. For instance, DL has been drawing criticisms for compromising cybersecurity as it is susceptible to attacks by hackers and to deceit (Li et al. 2019a, b, c, d; Norton and Qi 2017; Papernot et al. 2016). Nevertheless, DL modelling architectures suffer from some errors; in several instances, DL was found to misclassify or randomly classify images (Nguyen et al. 2015; Szegedy et al. 2015). To tackle these issues, it is pertinent to design models that internally create states that are equivalent to image-grammar (Zhu and Mumford 2006). In addition, Mühlhoff (2020) has argued that despite its much-extolled advantage of requiring minimal hand-tuning, DL, in fact, relies on microwork by humans, thereby calling it “a form of distributed orchestration of human cognition through networked media technology” (Mühlhoff 2020).

The uses of DL technologies in the contemporary world and their potential for further applications cannot be disregarded, despite some limitations. Many scholarly works have been undertaken to comprehensively review the applications of DL technologies across different sectors. Most review works focus on specific areas and implementations of DL (Arulkumaran et al. 2017; Gheisari et al. 2017; Pouyanfar et al. 2018; Vargas et al. 2017). Other reviews have surveyed DL architectures and algorithms in the context of specific applications, such as speech emotion recognition (Fayek et al. 2017; Pandey et al. 2019), text classification (Zulqarnain et al. 2020), early diagnosis of Alzheimer’s (Ortiz et al. 2016), electronic health records (Roberto et al. 2020; Xiao et al. 2018), medical image analysis (Akkus et al. 2017; Cao et al. 2019; Liu et al. 2019; Shoeibi et al. 2020), time series forecasting (Lara-ben and Carranza-garc 2021), aircraft maintenance, repair, and overhaul (Rengasamy et al. 2018), and land cover mapping (Pashaei and Kamangir 2020). With DL having gained momentum only recently, review articles on DL architectures encompassing the full scope of the field are still lacking. Dixit et al. (Dixit et al. 2018) provided a brief overview of seven of the most widely used DL architectures (deep neural networks, deep belief networks, recurrent neural networks, deep Boltzmann machine, restricted Boltzmann machine, deep autoencoders, and convolutional neural networks), a list of DL libraries, and some of the most common applications. However, as is perceivable, their paper is not a comprehensive review of existing architectures. In addition to the models discussed by Dixit et al. (2018), Sengupta et al. (2020) have covered generative adversarial neural networks and highlighted tests that can be undertaken before implementing different neural networks in safety–critical systems. Shrestha et al. (Shrestha 2019) provided a rigorous overview of the neural networks and DNNs and found certain limitations that constrain training, such as overfitting, long training time, and high susceptibility to getting stuck in the local minima.

Khamparia and Singh (2019) contributed perhaps one of the most important studies on DL architectures, even though it is limited to neural networks. Their meta-analysis critically reviewed twelve DL modelling techniques and found that advanced DL architectures that are combinations of a few conventional architectures are far more robust than their conventional counterparts. A comprehensive list of DL architectures and their related applications was also presented. Nevertheless, as a continuously expanding and developing field, there is a need to critically review and compile information on the state-of-art DL modelling techniques. Therefore, by first delving into a brief discussion on DL as a subset of ML, this paper comprehensively reviews all of the available DL modelling techniques. While these modelling techniques have many benefits across multiple disciplines, they are not without limitations. Therefore, this paper also highlights the advantages and drawbacks of these models and concludes with future perspectives on DL models, providing directions for enhancing the architecture designs and increasing the implementation of DL technologies across more sectors. Overall, this paper aims to disseminate essential information on the constantly evolving field of deep learning and direct future research towards improving existing modelling techniques.

2 Methodology for selecting, collecting, and analyzing pertinent data

This review utilized an integrative literature method to analyze almost all available deep learning modelling approaches, as well as their current progress, applications, advantages, and challenges. Throughout this method, relevant and reliable papers were selected, collected, filtered, carefully evaluated and analyzed. The database was found using credible websites, e.g. Scopus and refereed journals from reputable publishers such as Nature, Elsevier, Taylor & Francis, Springer, Wiley, ACS, Inderscience, MDPI, Frontiers, and Sage. Relevant keywords such as “Deep learning”, “Deep learning architecture”, “Deep learning modelling”, “Advantages of deep learning”, “Challenges of deep learning”, “Future of deep learning”, and each deep learning model such as “Vector space model”, “Convolutional neural network”, “Recurrent neural network” and so on, were used to find out publications related to the present work. Through the Scopus database, 186,154 papers published within the last five years were identified. The references and bibliographies of the aforementioned publications were sifted and compiled in order to locate more relevant papers. The following criteria were used to thoroughly scan and categorize the abstract, introduction, and conclusion from selected papers:

• (i) Preliminary consideration was given to only peer-reviewed articles from reputable publishers and websites

• (ii) Researchers who are actively engaged in the relevant research field were chosen and collected

• (iii) The selected publications were evaluated for their balance between modern studies and prior research

• (iv) Referring to websites that employ the aforementioned keywords commercially

• (v) The most recent and cutting-edge algorithms relevant to the present work were emphasised

• (vi) Some publications of relevance that were cited in recent studies were rigorously retrieved as the original source of the studies.

The above criteria assisted in selecting 748 papers that are more relevant. Throughout the entire review process of available relevant papers, several questions were raised. To answer these questions, some other references were sourced and examined for further clarification and improvement. Papers for the present study were chosen based on a set of inclusion and exclusion criteria, which are illustrated in Table 1. A total of 419 articles were finally selected by applying the exclusion criteria. Although the exclusion criteria appeared to provide a solid foundation to find peer-reviewed and high-quality academic articles, some of the characteristics of the exclusion criteria appeared to be biased and skewed, making it difficult to discover high-quality academic journals. The authors conducted a test–retest procedure to overcome this issue.

Table 1 Inclusion and exclusion criteria to select papers for the present review

3 Deep learning

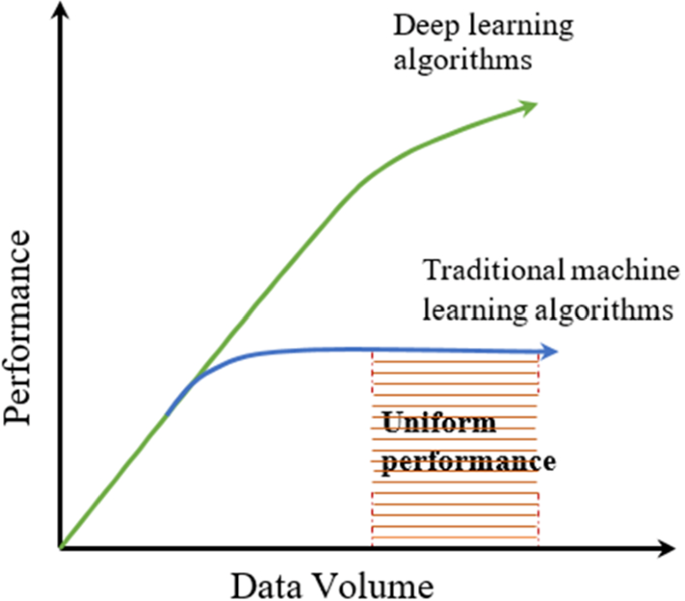
Deep learning (DL) is considered an evolution of machine learning (ML) that incorporates algorithms to learn from data to accomplish some tasks without being explicitly programmed (Lecun et al. 2015). Both ML and DL are a subset of artificial intelligence (AI). ML powers a wide range of automated functions in various businesses, from data security services hunting down malware to finance specialists looking for trade warnings. It has also a wide variety of applications in modern society, such as: developing intelligent personal assistants for finding helpful information (Dhyani and Kumar 2019), recommender systems that can suggest relevant items to the users (Zhang et al. 2019), machine translation to provide the most accurate translation of any text in any language (Poliak et al. 2018), and predicting the class of object in an image (Chen et al. 2018a; b). The way machines can learn new techniques becomes interesting whenever deep learning techniques are employed. The effectiveness of traditional machine-learning approaches is comparatively lower than DL techniques, as illustrated in Fig. 1, considering that they require a large volume of data to provide significant results. For a long time, designing a feature extractor for machine learning systems demanded hand-crafted features to simplify the learning process. However, such feature extraction techniques need human expertise and significant domain understanding.

Fig. 1

Performance of deep learning against traditional learning (Ng 2015)

Deep learning allows machines to learn from their mistakes and comprehend the world as a hierarchy of concepts. In this learning process, the machines learn from data using a general-purpose learning algorithm, thus needing less human expertise to describe all the knowledge that the machine requires expressly. The models of DL employ a layered network architecture, known as an artificial neural network (ANN) (Schmidhuber 2015), which is modelled after the human brain's analogous networks. The embedding of layers results in a significantly more efficient learning experience than traditional machine learning models. The ability of deep learning to achieve high-level features from a massive amount of input data, referred to as feature engineering, distinguishes it from machine learning. As a result, deep learning is gaining popularity with innovative applications in natural language processing (NLP), computer vision, and predictive modelling (Ahmad et al. 2019).

4 Deep learning modelling techniques

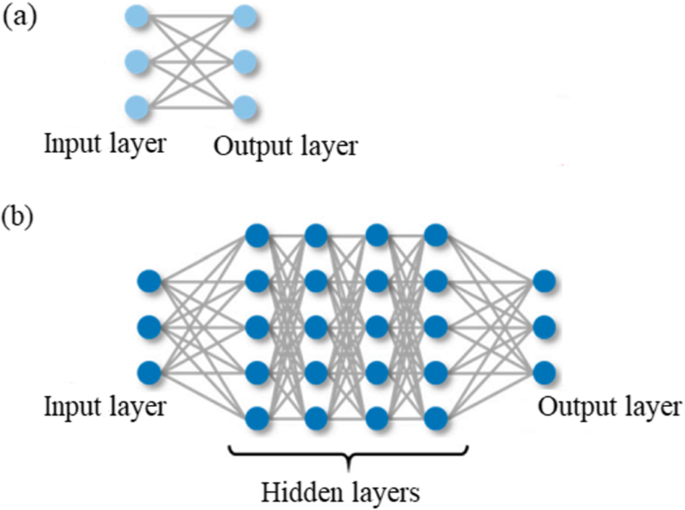
Deep learning modelling techniques enable computational models to learn feature representation in data using multiple processing layers and several levels of abstraction (Lecun et al. 2015). Artificial neural networks (ANNs) provide the foundation of advanced deep learning models (Schmidhuber 2015) and perform well in a variety of domains. However, ANNs suffer from certain drawbacks, such as no guaranteed convergence to an optimal solution and being prone to overfitting the training data. Therefore, researchers have tried to find solutions using deep architecture. The term “deep” in “deep learning” was motivated by the number of processing layers through which the data must pass in the network. A deep learning model is made up of multiple layers that stack up on top of each other (Fig. 2). The first layer (input) consists of units containing values fed to every neuron in the first hidden layer, then the predicted results come out of the model from the output (final) layer. The number of units in this layer equals the number of output classes desired. The hidden layers placed between the input and output layers apply weights to the inputs and pass them through an activation function. The activation function is used to help the network add non-linearity and learn complex relationships in the data. The backpropagation algorithm computes the error between the predicted result and the desired class in the output layer, then proceeds to the hidden layer to reduce the loss by adjusting the weights. This process is repeated until the output is accurate enough to be useful.

Fig. 2

a Conventional neural network b Deep learning neural network (Oka et al. 2021)

Considering the concepts of neural networks discussed above, several deep learning modelling techniques are built as described in the following subsections. These techniques have various applications, such as the detection, classification of objects in images and video data (Lea et al. 2016), finding sentiment and emotion from text data (Jin Wang et al. 2016a; Hassan et al. 2018; Majumder et al. 2019), audio processing applications like speech recognition (Rao et al. 2018a; b), and neural machine translation (NMT) with translation between different languages (Sutskever et al. 2014). Developing a deep learning-based model in these fields requires the pre-processing of raw data, feature selection, optimal parameter determination, and the evaluation of classification accuracy and convergence speed. This section covers different types of deep learning modelling approaches and explains their underlying mathematical concepts, advancements, latest implementations, and applications in various fields.

4.1 Vector space model

The vector space model (VSM) is an arithmetic model in which texts are represented as vectors. It has been successfully applied in information filtering, information retrieval, and other areas (Abualigah and Hanandeh, 2015; Van Gysel et al. 2018; Mitra and Craswell 2017). The vector elements describe the weights or importance of every word in a document. The cosine similarity technique can be applied to find the degree of similarity between two documents (Günther et al. 2016). In the vector space model shown below, documents are described as a term-document matrix (Shi et al. 2018) or a term-frequency matrix, where the rows represent the documents and the terms are defined by the columns. Words, sentences, or phrases are often used as terms, each of which depends on the application and context. Each cell signifies the term’s weight in a document, and if a term is present in the document, the cell value will be non-zero.

$$\left[\begin{array}{ccc}\begin{array}{c}\\ {D}_{1}\\ \begin{array}{c}{D}_{2}\\ \cdots \\ {D}_{n}\end{array}\end{array}& \begin{array}{c}{T}_{1}\\ {w}_{11}\\ \begin{array}{c}{w}_{12}\\ \cdots \\ {w}_{1n}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}{T}_{2}& \dots & {T}_{t}\end{array}\\ \begin{array}{ccc}{w}_{21}& \dots & {w}_{t1}\end{array}\\ \begin{array}{c}\begin{array}{ccc}{w}_{22}& \dots & {w}_{11}\end{array}\\ \begin{array}{ccc}\cdots & \cdots & \cdots \end{array}\\ \begin{array}{ccc}{w}_{2n}& \cdots & {w}_{tn}\end{array}\end{array}\end{array}\end{array}\right]$$

Suppose there is a document ${D}_{k}$ and a query $q$. The cosine similarity formula can be used to find the similarity between ${D}_{k}$ and $q$ using the formula:

$$\mathit{cos}\left({D}_{k}, q\right)= \frac{{\sum }_{i=1}^{N}{w}_{i,j}{w}_{i, q}}{\sqrt{{\sum }_{i=1}^{N}{{w}_{i,j}}^{2}}\sqrt{{\sum }_{i=1}^{N}{{w}_{i,q}}^{2}}}$$

(1)

The query and document vectors are not correlated if the cosine value gives zero in Eq. (1). The vector space model assumes that the terms are independent of each other. As a result, the model ignores the possibility of semantically related index terms.

4.1.1 Word embedding

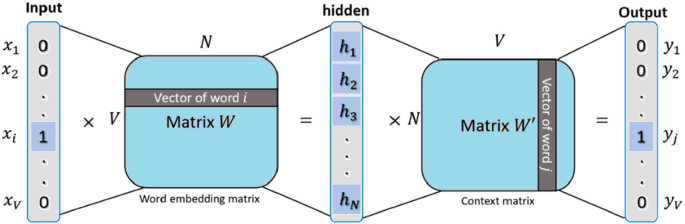
In recent years, research interest in the concept of using a vector representation of words and word embedding has increasingly progressed. The latter has been often utilized in advanced natural language processing applications, such as information retrieval, question answering (Zhou et al. 2016), and machine translation (Zhang et al. 2017a; b, c). Word embedding is a method of generating vectors and mapping them to associated words. Tomas Mikolov’s word2vec (Mikolov et al. 2013) models can generate high-dimensional vector representations of words when training on a large text dataset (Demeester et al. 2016). These vectors are capable of capturing syntactic and semantic information. In its simplest form, a word2vec model involves the training of a simple neural network to complete a task and includes only one hidden layer in the neural network, as shown in Fig.. The goal is to simply learn the hidden layers' weights, which are used as word vectors in many applications (Zhang et al. 2015). The size of the input layer depends on the number of words in the vocabulary for training, where one neuron represents one word. The hidden layer size is defined by how many dimensions we want to keep in the resulting word vectors. It is suggested that the dimensionality of the vectors be set between 100 and 1000 in the original model (Demeester et al. 2016). Higher dimensionality provides high quality of word embedding, while the output layer has the same size as the input layer.

To train the embedded weights, the continuous bag of words (CBOW) and skip-gram are two useful techniques. Given a target word, the skip-gram model attempts to predict alternative context words. Here, input to hidden layer connections remains the same as the word2vec fully connected network. However, a simple modification is made in the hidden to output layer connection to give space for the selected number of context words. Contrariwise, the CBOW model aims to predict target words given a set of context words, the number of which depends on the setting of the window size. For example, in the sentence, “the quick brown fox jumped over the lazy dog.”, ‘the’ and ‘brown’ might be used as context words and ‘quick’ as the target word. A tweak to the neural network architecture is required in this scenario as is a simple modification to adjust the input to hidden layer connection C times. Here, C is the number of context words. By adding these configurations to the network, the hidden layer's output can be found by taking the mean of the context words. The steps after calculating the hidden layer remain precisely the same. A text classification system was proposed by Ali et al. (2019) for retrieving transportation sentiment from social networking and news sites. The authors combined a topic2vec and word2vec to create a word embedding model that describes the documents using a low dimensional vector but keeps the semantic meanings. The model obtains a sentiment classification accuracy of 93% with transportation datasets, outperforming topic2vec document representation approaches. The model treats the unimportant words as sentiment words that cause decreasing classification performance. However, sophisticated data pre-processing is needed to improve classification accuracy (see Figs. 2, 3).

Fig. 3

Illustration of word2vec fully connected neural network (Orkphol and Yang 2019)

4.1.2 Sentence embedding

The sentence embedding model aims to produce a fixed-length continuous vector representing the entire input. A rough sense of the relative locations of the sentence vectors in the original vector space can be obtained from the figure. Similar sentences are close together in summary-vector space. Skip-thought is one of the popular sentence embedding models that demonstrates significant results in several tasks, including semantic similarity, paraphrase detection, image annotation (how well the sentences describe an image), and classifications (Kiros et al. 2015).

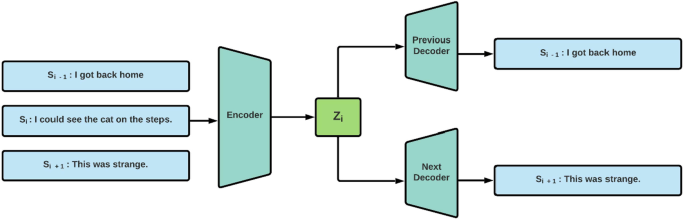
Vector representation, which is used for words, phrases, sentences, paragraphs, documents, or even images, can be generalized as representing “thoughts.” On the other hand, the skip-thought model abstracts skip-gram architecture to the sentence level (Kiros et al. 2015). The idea behind this model is that the context words embed a word's meaning. The model tries to map sentences with common syntactic and semantic information into similar vectors by reconstructing the neighbouring sentence. The skip-thought model has three main parts: encoder, previous decoder, and next decoder, as shown in Fig. 4.

Fig. 4

Skip-thought model overview (Hassan et al. 2018)

In Fig. 4, given a sentence ${s}_{i}$ at index $i$, the encoder produces a fixed-length representation ${z}_{i}$. It needs to access the word embedding layer (also called the lookup table layer) that maps each word into a corresponding vector. Inside an encoder, a recurrent neural network (RNN) with the gated recurrent unit (GRU) or long short-term memory (LSTM) activation is fed every word sequentially in a sentence. This encoder captures the temporal patterns of sequential word vectors. The previous decoder takes the embedding ${z}_{i}$ from the encoder and “tries” to generate the proceeding sentence ${s}_{i-1}$. This decoder uses another recurrent network that generates the sentence sequentially and shares the same lookup table layer from the encoder. The next decoder takes the embedding ${z}_{i}$ from the encoder and “tries” to generate the subsequent sentence ${s}_{i+1}$. This decoder also uses a recurrent network similar to the previous decoder. The encoder is the end result of the skip-thought model as it contains syntactic and semantic information.

Due to the vast amount of textual data surfacing online, the demand for text summarization is continuously increasing worldwide. As a result, the necessity of natural language processing (NLP) models arises to extract the essential and valuable information from the long text while maintaining critical information. Mohd et al. (2020) introduced a text summarizer that obtains the features of a long text document using different techniques, such as Latent Dirichlet Allocation (LDA) and Term Frequency-Inverse Document Frequency (TF-IDF), which represents each sentence as a numerical vector. Similar vectors are aggregated together using a genetic algorithm. Lastly, the LDA technique was utilized to obtain the center sentence of each cluster to be included in the resulting summary. The macro-average of precision from the experimental results was found to be 34%, which is higher than the benchmark standard. However, the technique was performed on only one dataset, and thus the precision may not be feasible.

Different types of difficulties, such as combining syntactic information or identifying different labels for the document classification task, are acknowledged using DocBERT. The DocBERT is a document classification model based on Bidirectional Encoder Representations from Transformers (BERT) (Adhikari et al. 2019). The general idea is to use a fully connected layer to filter the representation obtained from the common language specification (CLS) token and then employ a SoftMax layer to convert 768-dimensional encoding to class distribution. Adhikari et al. (2019) reported the state-of-the-art results on four popular datasets, attempting to address the BERT model's high computational expense and reduce the parameters by 30-fold. The average document length was found to be less than BERT, while the maximum length was 512. However, BERT can outperform non-contextual embeddings on various tasks, such as the clinical domain. Si et al. (2019) explored the performance of classic word embedding approaches (word2vec, GloVe) and contextualized methods (BERT) on a clinical concept extraction task. The output of the BERT model was fed into a bi-LSTM, which showed that contextual embeddings play a significant role in achieving better performance (F1-measures of 93.18) on various benchmark tests in the datasets like SemEval.

4.1.3 Graph embedding

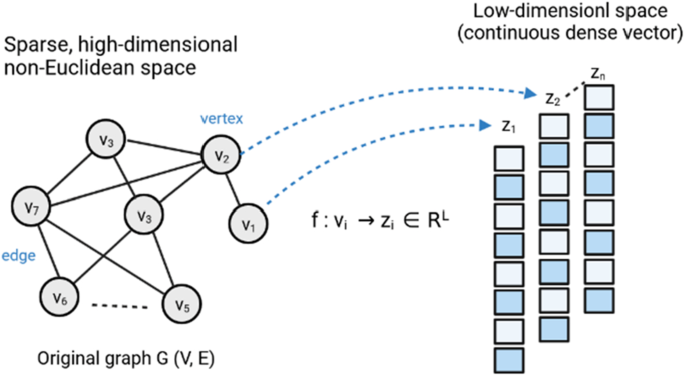
Graph embedding is a technique for transforming a whole graph into a single vector while preserving the graph's relevant information. The resulting vectors contain highly informative features that can be used for the task, such as node classification, ranking, alignment, link prediction, clustering, and visualization. The primary goal of graph embedding techniques is to reflect high-dimensional points into a residual continuous vector space with low dimensions (Fig. 5). As a result, it is easy to compute the node similarity using the dot product or cosine distance formula. Graph analytics is also considerably faster and more accurate than computing in the high-dimensional complex graph domain.

Fig. 5

Graph embedding (Xu 2020)

Although matrix-factorization approaches have been proposed to represent a node earlier, they are significantly affected by conventional dimension reduction techniques. Comparatively, recent techniques focus on learning node embeddings using random walk characteristics. A graph structure can be translated into a sample collection of linear sequences using the DeepWalk model (Perozzi et al. 2014), which employs hierarchical SoftMax techniques as the loss function. The primary concept underlying this method is to learn embeddings, and therefore (Hamilton et al. 2017):

$$DEC\left({z}_{i}, {z}_{j}\right)\triangleq \frac{{e}^{{z}_{i}^{T}{z}_{j}}}{{\sum }_{{v}_{k}\in V}{e}^{{z}_{i}^{T}{z}_{k}}}\approx {P}_{g}, T({v}_{j}|{v}_{i})$$

(2)

where ${P}_{g}, T({v}_{j}|{v}_{i})$ denotes the probability of visiting from vertex ${v}_{i}$ to ${v}_{j}$ on a length-T $;\mathrm{ and} DEC\left({z}_{i}, {z}_{j}\right)$ is a function that takes the node embeddings ${z}_{i}$ and ${z}_{j}$ and uses them to decode the graph metrics.

A hypergraph embedding method, LBSN2Vec, was developed by Yang et al. (2019) for location-based social network (LBSN) data that enhances friendship and location prediction task effectiveness. LBSN provides services to the users to publish their location and location-related contents like photos or notes. Encoding both users and places into low-dimensional vectors produces hyperedges by sampling friendships and checking-in using a random walk. The model chooses two nodes from the sample graph and then feeds the nodes into a model similar to skip-gram to generate low-dimensional vectors representing the nodes. The authors revealed that the LBSN2Vec model outperforms the baseline graph embeddings in predicting the friendship of two individuals and location prediction by 32.95% and 25.32%, respectively. However, the study was limited to random walk approaches for the location prediction task in the hypergraph. Further research is thus required to take advantage of the meta-graph or hypergraph for the deep learning-based recommendation model.

4.2 Convolutional neural network

Convolutional neural networks (CNNs) are particularly useful to reduce the number of parameters in an ANN. This has inspired researchers and practitioners to consider adopting larger models to accomplish tasks that were previously difficult to handle with regular ANNs. The CNN model is influenced by an animal's visual cortex and is intended to learn low-level to high-level features from the data received gradually. For example, the model first detects the low-level edge in the first layer in the image classification task and then the high-level features like shapes and faces in an image (see Fig. 5).

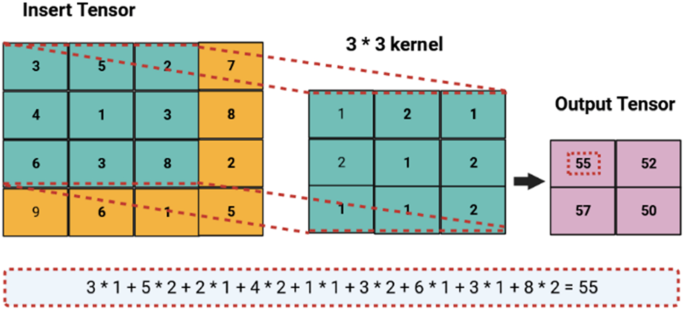
To understand the architecture of CNN, we explain the essential CNN model components. A CNN model is comprised of three primary layers: convolution, pooling, and fully connected layers. The first two layers generate features from the input, while the third layer, the fully connected layer, connects the extracted features to the final output. The convolution layers retrieve the high-level characteristics from the data provided. The primary objective is to compute different feature maps by projecting a tiny array of numbers called a "kernel" to the input data. The input is also known as a tensor. An element-wise product between each kernel element and the input tensor is performed at each position of the tensor. Then, the summation of these values is calculated and applied to the associated index of the output tensor (Fig. 6). Multiple kernels are used to repeat this process to produce an arbitrary number of feature maps. Each feature map represents distinct input tensors' characteristics, and each kernel can be considered as a different feature generator. The size and number of kernels are two primary hyperparameters that describe the convolution operation. Usually, the kernels' size is 3 × 3, but it can also be 5 × 5 or 7 × 7. The number of kernels is chosen arbitrarily depending on the depth of the output feature maps. Mathematically, convolution operation can be defined by the following equation (Khan et al. 2020):

$$f_{l}^{k} \left( {p, q} \right) = \mathop \sum \limits_{c} \mathop \sum \limits_{x,y} i_{c} \left( {x,y} \right) \odot e_{l}^{k} \left( {u, v} \right)$$

(3)

where ${f}_{l}^{k}$ is the output feature map of the $k$-th convolution operation of the $l$-th layer. This can be computed as ${F}_{l}^{k}=[{f}_{l}^{k}\left(\mathrm{1,1}\right), \dots {f}_{l}^{k}\left(p, q\right),\dots {f}_{l}^{k}(P, Q)]$, where ${i}_{c}$ is the input tensor and ${i}_{c}\left(x,y\right)$ is an element of that tensor. These values will be element-wise multiplied by ${e}_{l}^{k}(u, v)$, the $k$-th convolutional kernel of the $l$-th layer.

Fig. 6

Convolution operation

CNN introduces non-linearity to the network by applying a non-linear activation function. Previously, the popular choice was non-linear activation functions, including sigmoid or tangent functions (LeCun et al. 2012). However, to resolve the vanishing gradient problem (Nwankpa et al. 2018) of the sigmoid and tangent function, Rectified Linear Unit (ReLU) and its variants, such as leaky ReLU and Parametric Rectified Linear Unit (PReLU), are used. One of the recently proposed activation functions named Mish outperforms ReLU and other typical activation functions in many deep networks across benchmark datasets (Misra 2019). The activation function of the convolutional feature map can be computed as:

$${a}_{l}^{k}=g({F}_{l}^{k})$$

(4)

where ${F}_{l}^{k}$ is the output of a convolutional operation that goes to an activation function g(); and ${a}_{l}^{k}$ is the non-linear output of the k-th input feature map in the $l$-th layer.

The extracted features from the convolutional and pooling layers are flattened to a one-dimensional array of numbers. Those features are then fed into the traditional neural network, where each input is connected to its subsequent layer neurons by a learnable weight. The main drawback of a fully CNN is that it requires training many parameters, which contributes to its high computational expense and possible overfitting. The dropout technique is used to overcome such difficulties, in which a few nodes and connections are removed (Goodfellow et al. 2013). The output layer is the final layer of CNNs, where $softmax$ function is widely used to provide probability distribution (Russakovsky et al. 2015). Another classifier, the support vector machine (SVM), can also classify data (Tang 2013).

Parallel computing has made CNNs more efficient than humans in recognizing visual patterns, making them a desirable alternative for wide-area monitoring because of their advantages over humans. Mukherjee et al. (2020) proposed a CNN-based generative model, namely “GenInSAR”, for combined coherence estimation and phase filtering which directly learns interferometric synthetic aperture radar (InSAR) data distribution. InSAR is a developing and extremely successful remote sensing method for monitoring a variety of geophysical parameters, including surface deformation. The unsupervised training on simulated and satellite InSAR images of the proposed model (GenInSAR) outperformed the other comparable methods (CNN-InSAR(as-is), CNN-InSAR(retrained), NLSAR, NLInSAR, Goldstein, Boxcar) in reducing the total residue (by more than 16.5% on average), with fewer over-smoothing/artifacts surrounding branch cuttings. Compared to the related methods, the phase cosine error, coherence and phase root-mean-square-error of GenInSAR were improved by 0.05, 0.07 and 0.54, respectively. As a result, the InSAR machine learning can be improved by GenInSAR's ability to produce new interferograms.

4.2.1 CNN-LSTM

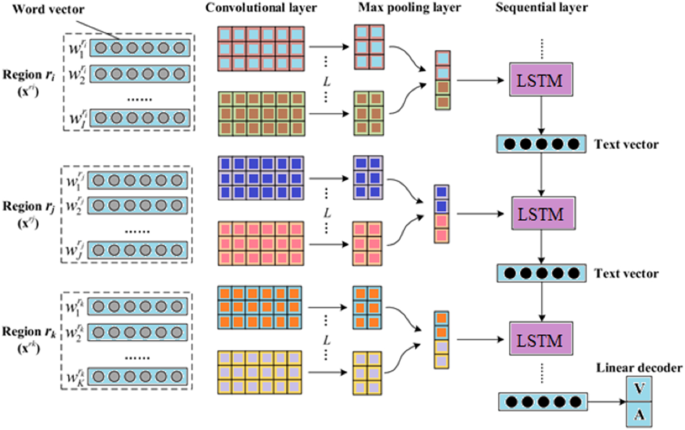
Long short-term memory (LSTM) can learn long-term relationships in data. However, spatial data like images are challenging to model with the standard LSTM. The convolutional neural network combined with long short-term memory (CNN-LSTM) is based on an LSTM network that is primarily designed for sequence prediction tasks where the input is spatial data, such as images, videos, or temporal structure of words in a sentence, paragraph, or document. The model shown in Fig. 7 illustrates the combined regional CNN and LSTM to identify the sentiment of text (Wang et al. 2016a), which considers an individual sentence as a region and long-distance relationship of sentences in the prediction task.

Fig. 7

Regional CNN-LSTM model for sentiment analysis (Jin Wang et al. 2016a)

The main architecture of the CNN-LSTM model consists of the input layer, convolution layer, pooling layer, sequential layer (LSTM hidden layer), and fully connected layer. The first three layers are the CNN layers. The CNN layer's output data is transferred to the LSTM layer. Following temporal modelling, the data from the LSTM layers are sent to a fully connected layer. These layers are well-suited to produce higher-order features that are easy to distinguish within distinct categories. The CNN model is used for feature extraction, while the LSTM model is employed for data interpretation over time.

4.2.2 Temporal convolutional network (TCN)

The novel work on the temporal convolutional networks (TCNs) was first proposed by Lea et al. (2016) for video-based action segmentation. This approach involves two phases: (i) CNN computes the low-level features that encapsulate spatial–temporal information, and (ii) RNN feeds the low-level features into a classifier to extract the high-level temporal information. Although TCN demands the integration of two different models, it offers a unified technique to capture all two layers of information in a hierarchical manner. The original TCN model possesses a convolutional encoder and decoder architecture. The model captures a set of video features as the input and then extracts a D-dimensional feature vector for each video frame. If a video has T frames, the input X appends all the frame-wise features in a way that $X\in {\mathbb{R}}^{T\times D}$. Similar to other CNN architectures, the networks apply some filters followed by non-linear activation of the input to extract features. The convolution consists of l layers, where the collection of filters in each layer is defined as ${\{{W}^{(i)}\}}_{i=1}^{{F}_{l}}$ for ${W}^{(i)}\in {\mathbb{R}}^{d\times {F}_{l-1}}$. Here, ${F}_{l}$ is the number of convolution filters in the l layer with a temporal window d. If ${X}_{l-1}$ is an output from the previous layer, the l-th layer output, ${X}_{l}$, can be calculated as follows (Kim and Reiter 2017):

$${X}_{l}=f(W*{X}_{l-1})$$

(5)

where $f$ denotes any non-linear activations functions, e.g., ReLu.

Convolutional neural networks and their variants are used in various applications, such as the detection, classification of objects in images and video data, finding sentiment and emotions in natural language data, and audio processing applications like voice recognition. A CNN-based architecture named LeafNet was developed by Barré et al. (2017) to identify plant species from the leaf images. The authors experimented with their model on three publicly available state-of-the-art datasets of leaf images: LeafSnap, Foliage, and Flavia. The previous studies on these datasets were based on the hand-crafted feature extraction technique. After data augmentation, approximately 270,000 leaf images were used on a 17-layer CNN to train the LeafNet model with image sizes of 256 × 256 pixels. Improved accuracies (by 0.8–13.3%) of 86.3%, 95.8%, and 97.9% were found on the LeafSnap, Foliage, and Flavia datasets, respectively, compared to previous studies. However, this method is comparatively slow (training takes about 32 h) and lacks context due to the small, cropped window sizes.

In another work, a region-based convolutional neural network (R-CNN) has been applied in the computer vision field for the object detection task. Li et al. (2019a, b, c, d) proposed the stereo R-CNN method that can perform three-dimensional (3D) object detection in autonomous vehicle navigation. The method identifies and integrates objects in both the left and right images simultaneously and uses a region-based object detection alignment to retrieve the correct 3D bounding box. The stereo R-CNN captures input images with a resolution of 600 × 2000 and takes advantage of ImageNet’s pre-trained ResNet-101. The model was evaluated on the KITTI object detection benchmark. The proposed method outperformed a previous study (Chen et al. 2018a, b) for 3D object proposals by over 25–30%. Due to the absence of precise depth information, the model can only produce shallow 3D detection results. Variations in appearance can also have a significant impact.

Chen et al. (2018a, b) introduced an unsupervised domain adaptation model for cross-domain object detection based on the faster R-CNN model (Zhang et al. 2016a, b). They employed two domain classifiers: one for high-level features at the global image scale and another for features clipped by the region proposal network at the instance (object) scale. The model was validated for different domain shift datasets. Via experiments, the authors found that the domain adaptive faster R-CNN model outperforms the faster R-CNN model by over 8.8%. This improvement was found consistent across the categories, thus indicating that the suggested method can minimize domain mismatch between object categories. However, the model was not trained to recognize traffic in darkness and is only adaptable to specific scenarios.

A dynamic CNN-based system was proposed by Chu et al. (2017) for tracking objects in videos. Using shared CNN features and Region of Interest Pooling, the model takes advantage of single object trackers. The experimental results showed that the proposed online multi-object tracking algorithm outperforms Markov decision processes by 4%. Although the model performed well in tracking objects, it is unsuitable for applications with limited resources. Also, the model may consume a lot of memory and time as it constructs a network for individual objects and performs online learning. Since CNN works well for both image classification and natural language processing tasks, CNN-based text classification models are gaining popularity. For instance, multi-layer CNN produces optimal features during the training process to reflect the semantics of the sentence being evaluated. These semantic constructs can be applied to a variety of applications, including text classification, text summarization, and information retrieval.

A CNN-based method was suggested by Hughes et al. (2017) for classifying clinical texts into one of 26 categories, such as “Brain” or “Cancer.” The model classifies texts by converting each document into a sentence-level representation. The authors used two stacked convolutional layers followed by a pooling layer. The experimental analysis revealed that the model improves the word embedding-based methods by accuracy of around 15%. However, the model was trained with a relatively small dataset (4000 sentences). To improve the model performance, domain adaptation techniques can be used to transfer knowledge from another domain to the medical field (Sun et al. 2016).

CNN-based models have also been successfully applied in the sentiment analysis of Twitter data. To predict user behavior via sentiment analysis, Liao et al. (2017) examined different deep learning techniques. They employed CNN and word embedding techniques to get better results than traditional learning algorithms, such as SVM and Naive Bayes classifiers. Their approach interpreted the sentence matrix to be the same as an image matrix. A linear kernel was convoluted to that sentence matrix, and a max-pooling function was applied to each feature to find the fixed-length representation of the sentence. The model was assessed on several benchmark datasets, including MR and STS Gold. The maximum development accuracy was found to be up to 74.5%. To improve the model accuracy, a multilayer CNN may be used instead of a simple CNN (single channel) for sentence classification.

CNN-based approaches are also becoming more prominent in cosmology because of their noticeable performance. DeepSphere is a graph-based CNN that works on cosmological data analysis (Perraudin et al. 2019) to predict a class from a map and classify pixels. The data often come as spherical maps represented as a graph in the network so that the model can perform the convolution and pooling operations. In the latter work, DeepSphere outperformed all the baselines by 10% in terms of classification accuracy. However, the model was applied to only the classification problem performed on scalar fields. To further demonstrate the performance of DeepSphere, it would be useful to make comparisons to various spherical CNN implementations with different sampling techniques.

4.3 Recurrent neural network (RNN)

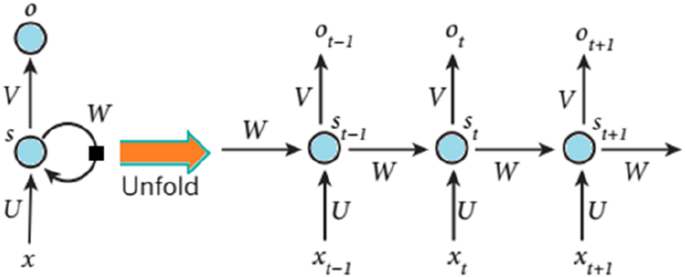
Recurrent neural networks (RNNs) have recently demonstrated promising performance on various natural language processing tasks and have produced superior results on multiple tasks, such as sentiment classification (Wang et al. 2016c), image captioning (Yao et al. 2017), and language translation (Li et al. 2017a; b). There are numerous situations in which data sequences describe the case itself. For example, in a language modelling task, a sequence of words defines their meaning. If the sequences are disturbed, the information makes no sense. In a traditional neural network, the assumption is that there has no dependency between the input and output. Considering this case, a network connecting to prior information is needed to fully comprehend the data. As a response, RNNs are useful, which are termed from the fact that they execute the same computation for each sequence element. The output in every state is dependent on the previous calculation. RNNs keep a "memory" that captures the information about what has been computed so far (Tomaš Mikolov et al. 2010, 2011). An RNN can be unfolded into an entire network, as illustrated in Fig. 8.

Fig. 8

Unfolded recurrent neural network (Lecun et al. 2015)

The computation flows running in an RNN for the text processing task are as follows:

• ${x}_{t}$ denotes the present input at time step t, where input is given as a one-hot encoded vector. For example, ${x}_{1}={\begin{array}{cc}[\begin{array}{cc}\begin{array}{cc}1& 0\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}& 0\end{array}]}^{t}$ is the initial word in a sentence.

• ${s}_{t}$ signifies the hidden state at time step t, captures the “memory of the network, and is computed using the previous hidden state and the present step's input:

  $${s}_{t}=f(U{x}_{t}+W{s}_{t-1})$$

  (6)

where $f$ is an element-wise non-linear function, such as $tanh$ or $ReLU$. In the case of calculating the first hidden state, ${s}_{t-1}$ is typically set to all zeros. W and U are the weight matrix of the hidden state and input, respectively.

• ${o}_{t}$ represents the output at time step t. For instance, to predict the next word in a sentence, the probability can be calculated by applying the $softmax$ function.

  $${o}_{t}=softmax(V{s}_{t})$$

  (7)

An RNN can, in theory, summarize all historical information up to time step ${s}_{t}$. Unfortunately, the accuracy of RNNs is significantly inhibited by the vanishing gradient problem (Bengio et al. 1994). To address this problem, gated recurrent units and long short-term memory have become more powerful models and gained acceptance in recent years as the best strategy to implement recurrent neural networks.

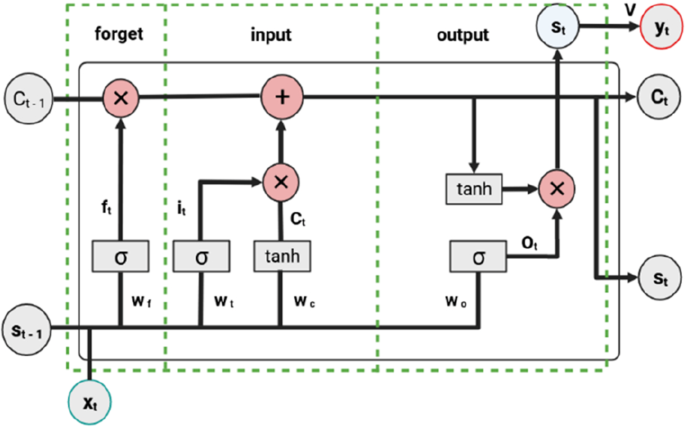
4.3.1 Long short-term memory (LSTM)

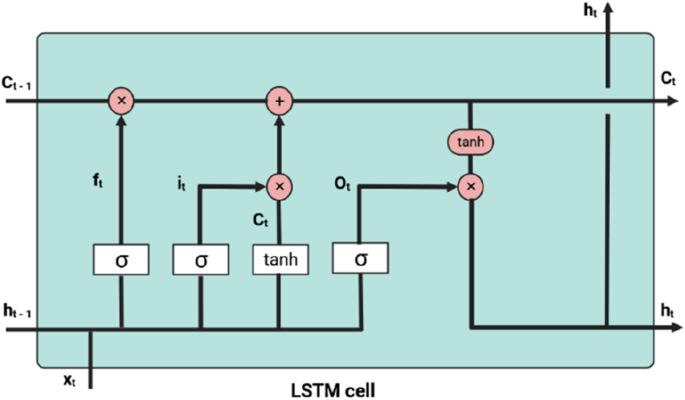
A long short-term memory (LSTM) network is comprised of different memory blocks referred to as cells. A cell is constructed by gates that control the flow of information: forget, input, and output gates (Fig. 9). A forget gate removes information from a cell configuration, and the input gate updates the newly entered data to the cell. The input gate determines the rate at which new data enter the cell, whereas the output gate limits the data in the cell and computes the output activation of the LSTM unit.

Fig. 9

A schematic for a long short-term memory cell (Jenkins et al. 2018)

The gating mechanism in a LSTM can be defined by the following equations:

$${i}_{t}=\sigma ({W}^{i}{x}_{t}+{U}^{i}{h}_{t-1}+{b}^{i})$$

(8)

$${f}_{t}=\sigma ({W}^{f}{x}_{t}+{U}^{f}{h}_{t-1}+{b}^{f})$$

(9)

$${o}_{t}=\sigma ({W}^{o}{x}_{t}+{U}^{o}{h}_{t-1}+{b}^{o})$$

(10)

$${\widetilde{C}}_{t}=tanh({W}^{g}{x}_{t}+{U}^{g}{h}_{t-1}+{b}^{g})$$

(11)

$${C}_{t}= {f}_{t}\otimes {C}_{t-1}+{i}_{t}\otimes {\widetilde{C}}_{t}$$

(12)

$${h}_{t}= {o}_{t}\otimes tanh({c}_{t})$$

(13)

where ${i}_{t}$ is input gate; ${f}_{t}$ denotes forget gate; ${o}_{t}$ is output gate at a time step t; ${\widetilde{C}}_{t}$ is a new memory cell vector; and W and U are parameter matrices.

4.3.2 Bidirectional long-short time memory (BiLSTM)

Regular recurrent neural networks with LSTM cells can be extended to bidirectional recurrent neural networks in which the data is passed through two LSTMs (Graves et al. 2013; Graves and Schmidhuber 2005). One forward LSTM offers the input sequence in the correct order (forward layer), and another backward LSTM provides the input sequence in reverse order (backward layer). This technique improves the model's accuracy by capturing the long-term dependencies of the input sequence in both directions. In the BiLSTM, the forward layer computation is identical to those in the regular LSTM that computes the sequences ($\overrightarrow{{h}_{t}}, \overrightarrow{{c}_{t}}$) from $t = 1 to T$. On the other hand, the backward layer computes the sequences $\overleftarrow{{h}_{t}, }\overleftarrow{{c}_{t}}$ from $t = T to 1$ as described below:

$$\overleftarrow{{i}_{t}}=\sigma ({W}^{i}{x}_{t}+{U}^{i}{h}_{t+1}+{b}^{i})$$

(14)

$$\overleftarrow{{f}_{t}}=\sigma ({W}^{f}{x}_{t}+{U}^{f}{h}_{t+1}+{b}^{f})$$

(15)

$$\overleftarrow{{o}_{t}}=\sigma ({W}^{o}{x}_{t}+{U}^{o}{h}_{t+1}+{b}^{o})$$

(16)

$$\overleftarrow{{\widetilde{C}}_{t}}=tanh({W}^{g}{x}_{t}+{U}^{g}{h}_{t+1}+{b}^{g})$$

(17)

$$\overleftarrow{{C}_{t}}= \overleftarrow{{f}_{t}}\otimes \overleftarrow{{C}_{t+1}}+\overleftarrow{{i}_{t}}\otimes \overleftarrow{{\widetilde{C}}_{t}}$$

(18)

$$\overleftarrow{{h}_{t}}= \overleftarrow{{o}_{t}}\otimes tanh(\overleftarrow{{c}_{t}})$$

(19)

In a study conducted by Siami-Namini, Tavakoli, and Namin (2019), LSTM and BiLSTM were compared in terms of time series data modelling. The prediction accuracy of the BiLSTM-based model was 37.78% higher than that of standard LSTM-based models after training with both directions of input data. However, BiLSTM-based models achieved slower performance than the LSTM-based models. Another study (Brahma 2018) introduced a new model suffix bidirectional LSTM (SuBiLSTM) that improved BiLSTM for sentiment classification and question classification tasks (see Figs. 7, 8, 9).

4.3.3 Gated recurrent unit (GRU)

The architectures of a gated recurrent unit (GRU) and long short-term memory (LSTM) are closely related, since both are crafted similarly and, in some situations, generate equally outstanding results (Murali and Swapna 2019). The GRU cell is comprised of two gates: an update gate z and a reset gate r. It addresses the vanishing gradient problem of a regular RNN by using the update gate to determine how much historical memory (from earlier time steps) should be maintained and proceed to the future and the reset gate to pair the new input with the prior memory, as shown in Fig. 10.

Fig. 10

Gated recurrent unit cell (Zhao et al. 2019)

The gating mechanism in GRU is expressed by the following equations:

$$z= \sigma ({W}_{z}{h}_{t-1}+{U}_{z}{x}_{t})$$

(20)

$$r= \sigma ({W}_{r}{h}_{t-1}+{U}_{r}{x}_{t})$$

(21)

$$c=\mathit{tan}h\left({{W}_{c}(h}_{t-1}\otimes r\right)+{U}_{c}{x}_{t})$$

(22)

$${h}_{t}=\left(z\otimes c\right)\otimes ((1-z)\otimes {h}_{t-1})$$

(23)

where ${x}_{t}$ is the input vector; ${h}_{t}$ is output vector; W and U are parameter matrices; $\sigma$ is the sigmoid function; and $\otimes$ denotes the Hadamard product (entry-wise product).

Due to their versatility in various applications, RNNs have been successfully used in multiple tasks, including language modelling, speech-to-text processing, caption generator, machine translation, and other fields. RNN has also been applied in the sentiment analysis task to produce effective outcomes. For instance, Basiri et al. (2021) proposed a model to determine the sentiment from long reviews and short tweet text. In the model, the attention mechanism in RNNs is used to pay more attention to certain factors by assigning different weights when processing the data. The linguistic structures become more descriptive by applying the attention mechanism. Two bidirectional LSTM and GRU are also employed to generate the input text's previous and next contexts feature representation. The proposed model improved the accuracy from 1.85% to 3.63% for five long review datasets and from 0.25% to 0.54% for three short tweet datasets. While the study emphasized sentiment classification at the document level, there is potential to investigate sentiment classification at the sentence and aspect levels.

Another RNN model based on dialogue was built with an attention mechanism for emotion detection in textual conversations with six emotion labels (Majumder et al. 2019). The model has several variants, including DialogueRNN + Att and BiDialgouRNN, and considers both context and speaker information. The network employs three GRUs to track individual speaker states, global context from the preceding utterances, and the emotional state through the conversations. The data are provided and fed into the GRU for emotion representation, depending on the context. Although the DialogueRNN model achieved a better f1-score of 6.62% on several experiments, which is above the baselines (Majumder et al. 2019), it is time-consuming for training and not parameter-efficient for global or local contexts.

In RNN-based neural machine translation (NMT), sequence-to-sequence (seq2seq) architectures are used to deal with translation between languages. These seq2seq architectures apply two RNNs, namely an encoder and decoder. A study (Camgoz et al. 2018) utilized the standard seq2seq model to recognize sign language gestures from a video of someone performing continuous signs. In the study, the CNN was trained on the sentence level annotation to extract features from the video before translating it to text. These features were fed to the seq2seq model. The model scored 18.13 on the BLEU-4 matric (Papineni et al. 2001) and 43.80 on the ROUGE matric (Lin 2004). The model assumed that the CNN could learn good feature representation, but this hypothesis’s validity was not evaluated.

To model long texts for generating semantic relations between sentences, researchers face challenges in sentiment analysis. Rao et al. (2018a, b) handled the problem by proposing the State Refinement-LSTM (SR-LSTM) and SSR-LSTM models based on deep RNN. The models have two hidden layers: the first one uses LSTM to represent the semantic relationship of sentences, and the second one encodes those sentence relationships at the document level. The SR-LSTM model outperformed other models by obtaining an accuracy of 44% and 63.9% on the IMDB and yelp2015 datasets, respectively, while the SSR-LSTM model achieved an accuracy of 44.3% and 63.8% on the same datasets. However, the models considered only the sequential order of the documents. In future works, it may possible to represent the documents using tree-structured LSTM.

RNNs have also been successfully applied in intelligent health care systems. For example, Uddin et al. (2020) presented a multi-sensors data fusion network that relies on a recurrent neural network to recognize human activities and behavior. They extracted features from multiple body sensors and enhanced the features using Kernel Principal Component Analysis (KPCA) techniques. Then, human activities were recognized by training a deep RNN. The proposed method was assessed on three publicly available datasets. The average performance was found to be 99% using precision, recall, and F1-score matrices. It is possible to extend the work by developing a real-time human behavior tracking system with considering more complex human activities.

The RNN-LSTM approach for time series modelling has recently attracted much interest. The applicability of RNN-LSTM was analyzed by Sahoo et al. (2019) for predicting daily flows during the low-flow periods. The model effectively used the time series data by taking advantage of the LSTM memory cell to learn features from both the current and past values of an observable object. The model’s performance (root-mean-square error RMSE = 0.487) on hydrological data outperformed the traditional RNN model (RMSE = 0.516) and naive method (RMSE = 0.793). Nevertheless, multiple hidden LSTM layers can be used to enhance the performance of the model. Experts are also attempting to use deep learning approaches in typhoon prediction as deep learning techniques become more sophisticated. Alemany et al. (2019) proposed a fully connected RNN to predict hurricane trajectories from historical cyclone data that could learn from all types of hurricanes. The model produced better prediction accuracy than the previous models. For example, the mean absolute error (0.0842) of the RNN model was better than that of the previous sparse RNN average model (0.4612) to track Hurricane Sandy in 2012. The model may take advantage of converting the grid locations to latitude–longitude coordinates to reduce the conversion error.

4.3.4 Deep echo state network

The deep echo state network (DeepESN) is a recently proposed technique to enhance the efficiency of a general echo state network (ESN) in several domains. ESN is a reservoir computing model in which the reservoir computing shows efficiency to train RNNs by preserving memory using its recurrent nature. A dynamic reservoir is incorporated in ESN, presenting a sparsely linked recurrent network of neurons that differs from a traditional multilayered neural network. The reservoir is the network's only hidden layer, and its input connections are assigned at random and cannot be trained. On the other hand, the weights between the reservoir and output are the only ones that can be trained. The system learns the weights by linear regression rather than backpropagation. DeepESN is simply the ESN model's application of the deep learning architecture.

The DeepESN output is produced using a linear structure of the recurrent units across all recurrent layers. After initialization, the DeepESN reservoir component is left untrained. Therefore, the usual ESN technique is subject to stability limitations. Such limits are stated in DeepESN by the criteria for the ESN of the deep reservoir computing network. In the deep echo state network, input is processed by the first layer, and the previous layers’ outputs process the successive layers’ inputs. Therefore, the state transition function of a DeepESN can be presented by the following equation (Lukoševičius and Jaeger 2009):

$${x}^{\left(l\right)}\left(t\right)=\left(1-{a}^{\left(l\right)}\right){x}^{\left(l\right)}\left(t-1\right)+{a}^{(l)}\mathrm{tanh}({W}_{in}^{\left(l\right)}{i}^{\left(l\right)}\left(t\right)+{\theta }^{\left(l\right)}+{\widehat{W}}^{\left(l\right)}{x}^{\left(l\right)}\left(t-1\right))$$

(24)

where $l$ represents the number of layers; ${W}_{in}^{(l)}$ refers to the input matrix for $l$; ${\theta }^{(l)}$ denotes bias weight vector; and ${\widehat{W}}^{(l)}$ expresses the recurrent weight matrix for layer $l$. Here, ${i}^{\left(l\right)}(t)$ signifies the input for the l th layer of the network at time $t$. The output of the model can be expressed by the following equation:

$$y\left(t\right)={W}_{out}{[{x}^{\left(1\right)}\left(t\right){x}^{\left(2\right)}\left(t\right)\dots {x}^{({N}_{l})}]}^{T}+ {\theta }_{out}$$

(25)

where ${W}_{out}$ is the weight matrix between the reservoir and output $y(t)$.

Based on the DeepESN, a novel technique was developed by Gallicchio et al. (2018a) for diagnosing Parkinson’s disease. This is a significant initial work in the DeepESN domain that shows the superiority of DeepESN over the shallow echo state network model. The proposed technique identified Parkinson’s disease by using the time series data gathered from a tablet device while subjects performed sketching spiral tests with a pen. The acquired data contain x and y components of the pen, pen pressure, and grip angle. These signals were used to feed the model with no feature extraction and data pre-processing. The proposed model was evaluated on a public spiral test dataset and showed to perform better than the shallow ESN and other state-of-the-art methods.

Gallicchio et al. (2018b) proposed a DeepESN technique based on additive decomposition for predicting the time series data where the additive decomposition technique was used as a pre-processing step to the model. Data are split into three parts by additive decomposition (trend, seasonality, and residual) and then fed to the DeepESN. The performance of the additive decomposition-DeepESN was compared with LSTM, GRU, ESN, and DeepESN algorithms on six different datasets. The proposed model demonstrated significant performance for large, multidimensional data. Although ESN was found to be computationally efficient, it delivered a poor performance in prediction. LSTM and GRU required five times more computational time than DeepESN and additive decomposition-DeepESN. The additive decomposition-DeepESN model showed a low standard deviation, proving its stability, whereas other reservoir algorithms were unstable, i.e., with a higher standard deviation. Thus, the additive decomposition technique has the ability to improve the stability and performance of the DeepESN.

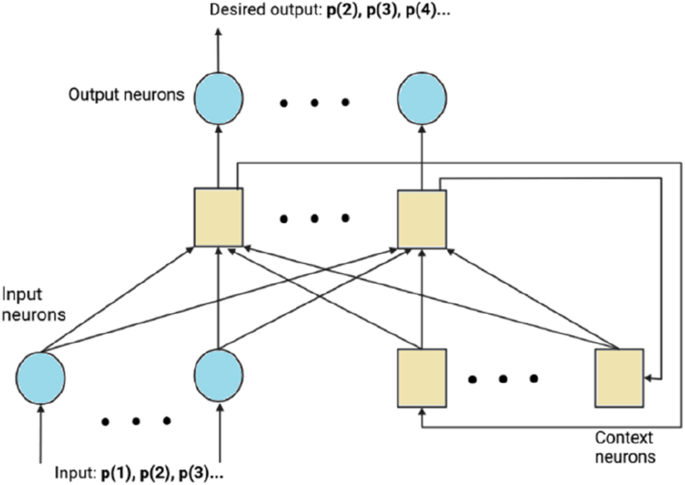
4.3.5 Elman recurrent neural network

The difference between the Elman recurrent neural network (ERNN) (Elman 1990) and other recurrent networks is that the hidden layer’s output is used as input for the context layer in the former. The architecture of ERNN consists of four layers: input layer, recurrent layer, hidden, and output layer. Each layer has one or multiple neurons that use a non-linear function of their weighted sum of inputs to transfer information from one layer to the next. Each hidden neuron is linked to a neuron of the single recurrent layer with the constant weight of one. As a result, the recurrent layer contains a copy of the hidden layer's state one instant ago. The benefit of using ERNN is that it emphasizes the relationship between future and previous values even when it is difficult to learn from them. The ERNN can be described by the following equations (Achanta and Gangashetty 2017):

$${h}_{t}=f\left({W}_{i}{x}_{t}+ {Wh}_{t-1}+ {b}_{h}\right)$$

(26)

$${y}_{t}=g({Uh}_{t}+{b}_{o})$$

(27)

where ${W}_{i}$ signifies hidden weight’s input; $W$ denotes the recurrent weight matrix of the hidden layer; ${b}_{h}$ represents the hidden bias; $U$ refers to the hidden output matrix; ${b}_{o}$ is the Bias Vector of the output layer; and $f$ and $g$ are the non-linear functions of hidden and output layers, respectively. Input is represented by ${x}_{t}$, the state of ${h}_{t}$ and ${y}_{t}$ refer to the outputs at time t.

An ERNN model with a stochastic time effective function (ST-ERNN) was developed by Jie Wang et al. (2016b) to forecast stock indices. The architecture is built by combining ERNN, multilayer perceptron, and stochastic-time-effective function, where a stochastic process is used to describe the level of historical data impact in the market. The time-strength function includes a drift function and Brownian motion to model the appearance of random changes while keeping the primary trend. The proposed neural network performs better than other existing neural networks in financial time series forecasting. Considering the rapid changes in the stock market data that make the field non-linear and nonstationary, predicting this kind of data is very challenging. Nevertheless, ST-ERNN showed a significant performance that can be crucial for future experiments in this domain. Krichene et al. (2017) applied ERNN for forecasting Mackey Glass time-series elements. The performance of ERNN was evaluated via comparison with two other existing models (Al-Jumeily et al. 2014; Park 2010) using the same dataset, where ERNN showed better performance. It is worth noting that optimal performance was achieved when the weights of the context units were randomly initialized.

4.4 Recursive neural network

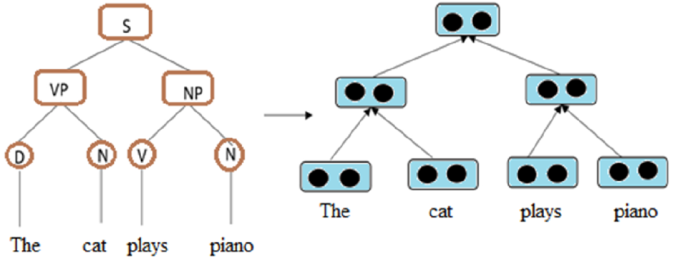
A recursive neural network (RvNN) is a nonlinear model that can function on structured inputs and is applicable to parse trees in natural language processing (NLP), image analysis, protein topologies, among other applications in structured domains. For instance, RvNN performs extremely well in the NLP tasks. Despite their deep structure, the architecture of RvNN lacks the capacity for hierarchical representation (Irsoy and Cardie 2014) and contains complex informative processing models. Because they acquire high-level representations from explicit inputs, recursive networks are effective in many deep learning tasks where the input is a structure. RvNNs are normally defined on a directed positional acyclic graph (Micheli et al. 2007). The form of RvNN is shown in Fig. 11, referring to the parse tree on the left side (Ma et al. 2018). If the parent node’s feature vector is $p,$ and $c1$ and $c2$ are its children, then

$$p=f(w.\left[c1;c2\right]+b)$$

(28)

where $f(.)$ is the activation function. The computation is recursively done for all nodes, and the hidden vectors of nodes’ can then be used for different classification tasks.

Fig. 11

The tree and its associated RvNN architecture (Ma et al. 2018). In the figure, S represents a sentence, NP is a noun phrase, VP is a verb phrase, D denotes determiner, N signifies noun, and V is a verb

Tree-structured recursive neural networks (RvNNs) were used to perform rumor detection on Twitter by Jing Ma, Gao, and Wong (2018). This study constructed two recursive networks on top-down and bottom-up tree-structured neural networks. Rather than a sentence’s parse tree, the model's input is a propagation tree rooted from a source post, and each node is a sensitive post rather than individual words. Recursive feature learning can capture the content semanticization of posts along with the tree structure and the receptive relationship between them. The basic concept of the bottom-up model is to create a feature vector by traversing each node recursively from the leaves to the root on the top. On the other hand, the concept of the top-down approach is to create an enhanced feature vector for each post, considering its propagation direction, in which rumor indicators are combined along the path of propagation. However, for the non-rumor class, the proposed models did not perform well. Yet, they could add other types of data into the structured neural models, such as user properties, to boost representation learning even further.

Biancofiore et al. (2017) analyzed atmospheric particulate matter (PM) and forecasted daily averaged concentrations of PM10 and PM2.5 up to 1–3 days. Particulate matter is a significant pollutant that affects human health, thus studies on reducing PM are critical. The latter researchers implemented a multiple linear regression model, feed-forward neural network, and neural networks with the recursive structure and found that the recursive neural network model outperforms the other methods. The total number of input variables and neurons in the second layer in the model determines how many neurons are in the first layer. The network’s output, the predicted particulate matter concentration, is represented by a single neuron in the final layer. In the latter work, the RvNN model correctly predicted 95% of the days, but this decreased to 57% when considering only the days where the limits were exceeded. In addition, the false-positive rate was 30% in this study.

Lim and Kang (2018) extracted the relation between chemical compounds and genes. They experimented with three methods, a tree-LSTM model with a position feature and a subtree containment feature, and implemented an ensemble process. The authors also implemented a stack augmented parser interpreter neural network (SPNN). The study revealed that the SPNN with ensemble technique outperformed the tree-LSTM with ensemble technique, which means that the extra tracking layer is beneficial. However, the proposed model is unable to comprehend the structure of a sentence. More training instances are needed to resolve this error. Also, coordination was not detected, whereby a comma, parenthesis, or special term like “and” or “or” is used to express coordination relations. This form of error may be avoided with the use of a separate module that looks for terms of equal emphasis.

4.5 Neural tensor network

In several natural language processing tasks, neural tensor networks (NTNs) have been successful. However, they need to estimate a considerable number of parameters, often resulting in overfitting (Yang et al. 2015) and excessive training times. An NTN model constructed by Socher, Chen, et al. (2013) implements a 3D tensor for combining two input vectors as bellow:

$$f({x}_{1}^{T} {W}^{\left[1:k\right]}{x}_{2}+V\left[ \begin{array}{c}x1 \\ x2\end{array}\right]+b)$$

(29)

where ${W}^{[1:k]}\in {\mathbb{R}}^{nxnxk}$ is the tensor ($W$ is a slice matrix); $V \in {\mathbb{R}}^{k \times 2n}$ is the linear mapping to combine input vectors x₁ and x₂; $b$ refers to a bias term; $f$ is the non-linear activation function; and ${x}_{1}^{T}{W}^{[1:k]}{x}_{2}$ is an array of $k$ bilinear products.

In contrast to the regular neural network model, NTN can connect two input vectors with a tensor directly. Although the NTN model is efficient, it takes considerable time to compute. Several studies were done to reduce the time complexity using parameter reduction techniques. For instance, Ishihara et al. (2018) introduced two-parameter reduction techniques based on the matrix decomposition method, while Y. Zhao, Liu, and Sun (2015) and P. Liu, Qiu, and Huang (2015) proposed simple matrix decomposition techniques for reducing parameters. A neural tensor model named the convolutional NTN converts all word tokens into vectors with the help of a lookup layer, encode questions and answers with coevolutionary, pooling layers to fixed-length vectors, and finally modelling their interactions with a tensor layer. Therefore, in a semantic vector space, this model will group related questions and answers to avoid the problem of lexical distances.

Qiu and Huang (2015) proposed a convolutional NTN for community-based question answering, integrating sentence modelling and semantic matching into one model. They implemented contrastive max-margin criterion to train the model. This study evaluated two different datasets for English and Chinese languages and found that the proposed model can handle more complex interactions with tensor layers than existing models. However, texts were converted into fixed-length vectors with the proposed convolutional layer, saving the essential information lost in bag-of-words. The experiments on the Chinese dataset demonstrated worse performance than the English dataset, which may be due to some mistakes in the segmentation of the Chinese expression.

A deep attention NTN for visual question answering was introduced by Bai et al. (2018). In this approach, tensor-based representations are used to find the joint relationship between images, questions, and responses. The authors used bilinear features to model images and questions that were further encoded by third dimension, i.e. the response as a triplet. The correlation between various triplets was broken down by different types of answers and questions. For the most discriminatory inference reasoning method, a slice-wise attention module was developed. The model was optimized by learning a label regression with Kullback–Leibler divergence losses. This designing technique enabled fast convergence and scalable training across a wide range of answer sets. The proposed model structure was integrated into the known visual question answering models MLB (Kim et al. 2017) and MUTAN (Ben-Younes et al. 2017). The proposed technique showed more accuracy than independent MLB and MUTAN models. This study compared GloVe word embedding with the word embedding learned from the proposed model and demonstrated that the model could be applied to more visual question answering models for further verification.

Hu et al. (2017) proposed enhanced face recognition performance by combining face recognition features and facial attribute features in a variety of tasks. They created a robust tensor-based model that develops fusion as a problem of tensor optimization. Due to the great number of parameters, the model was not effective in explicitly optimizing this tensor, and therefore a rich fusion architecture was proposed on the basis of the tensor. The results revealed that this tensor-based fusion’s Tucker-Low-Rank decomposition has the same Gated Two Stream neural network, making neural network learning simple but effective. The authors experimented on three well-known databases (MultiPIE, CASIA NIR-VIS2.0, and LFW) and found that the fusion approach significantly increased the face recognition performance. This technique can be expanded to large-scale data utilizing effective Mini Batch SGD-based learning since they set the equivalence between tensor-factorization and gated neural network architecture. Another advantage is that this model can be expanded to deeper architectures.

4.6 Continuous-bag-of-word with denoising autoencoder-logistic regression

To analyze sentiments, a Multimodal Learning technique was presented by Baecchi et al. (2016) by implementing neural network-based models for microblogging contents that might consist of texts and images. The proposed architecture is based on the continuous-bag-of-word (CBOW) model (Mikolov et al. 2013) and was further extended to include a denoising autoencoder (DA) to include visual data. Thus, CBOW-logistic regression (LR) is the extended version of CBOW. The difference between CBOW and the extended model is that the new architecture can perform classification and representation concurrently. The idea behind this approach is that the multi-tasking technique can develop the performance of a neural network, while the proposed model can incorporate semantic and sentiment polarity. The model was further extended to CBOW-DA-LR to include visual data, such as images in tweets. The descriptor acquired by the denoising autoencoder, along with the regular word presentation, provides a new descriptor for a word window in the tweet and learns a logistic regressor at the same time. The proposed CBOW-DA-LR technique was compared to SentiBank, a commonly-used approach in this domain, and showed higher accuracy (79% accuracy on text + image data vs. 72% of SentiBank). Although this specific technique shows significant improvements, it should be further evaluated to ensure its validity.

4.7 Deep belief network

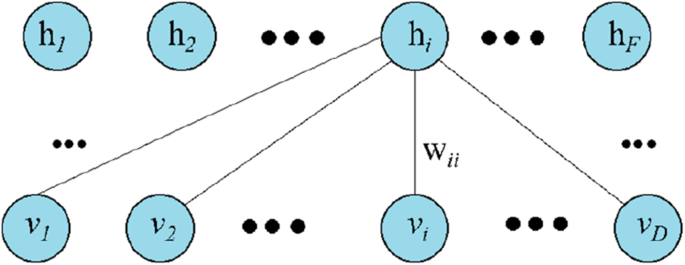
A deep belief network (DBN) is used to stack several unsupervised networks utilizing the hidden layer of each network for the next layer's input. A stack of restricted Boltzmann machines (RBMs) is typically used in the DBN. The benefit of the restricted Boltzmann machine is to fit the sample features (Hinton 2009). Therefore, a hidden layer’s output in an RBM can be used as another RBM’s visible layer input. This method may be considered as the further extraction of the features from the extracted features of the samples.

Suppose that $W$ is the generative weights of the hidden layers learned by an RBM denote $p(v|h,W)$ and prior distribution over hidden vectors $p(h|W)$. If $v$ is the visible vector, then the probability of $v$ can be expressed by the equation:

$$p\left(v\right)=\sum_{h}p\left(h|W\right)p(v|h,W)$$

(30)

where $p(v|h,W)$ is kept after learning W; and $p(h|W)$ is replaced by a more reliable model of the grouped following distribution on hidden vectors.

A computer-aided diagnosis system was built by Abdel-Zaher and Eldeib (2016) for detecting breast cancer, utilizing a weight-initialized backpropagation neural network from a trained DBN having identical architecture. The authors implemented DBN in an unsupervised state for acquiring the input features from the main Wisconsin breast cancer dataset. The obtained network weight matrix of DBN was then shifted into the backpropagation neural network to enroll the supervised state. In the supervised form, the backpropagation neural network was evaluated on Levenberg Marquardt and Conjugate Gradient algorithms. The proposed methodology showed 99.68% accuracy, which outperforms prior studies. Therefore, this work proposes an efficient system to construct an accurate breast cancer classification model. However, a deep belief network needs significant computational effort on hardware, and thus building a real-life computer-aided diagnosis system based on DBN is very challenging.

Zhao et al. (2017) proposed a feature learning technique named discriminant DBN for synthetic aperture radar (SAR) image classification. In the study, discriminant features were obtained in an unsupervised way by integrating the ensemble-learning technique with a DBN. Some SAR image patch subsets were organized and labelled for training weak classifiers, then the particular patch was defined by projection vectors. The SAR image patch was projected into each weak decision space covered by weak classifiers. The model’s performance was found to be better than other proposed approaches in this domain. However, since fixed neighbors govern the model, the weak classifier's training strategy's neighbor selection process may cause significant variance in pseudo-labelling. Some adaptive strategies can be utilized to choose specific samples for training the weak classifiers.

Another deep belief network, namely convolutional deep belief network (CDBN) is a hierarchical generative model for a real size image. RBM and DBN find it challenging to scale to complete pictures since they do not take into account the 2D form of the image, and therefore, the weights for detecting a specific feature must be acquired separately for each position. CDBN addresses this issue by scaling to the size of real images. The key to this solution is probabilistic max-pooling, a new strategy for shrinking higher layer representations in a probabilistically sound manner. This model stacks convolutional RBMs (CRBMs) to construct a multilayer structure similar to DBNs. The CRBM is analogous to RBM, except the weight among the hidden and visible layers is distributed over each position in the image. By integrating the energy functions of all individual layer pairs, the system generates an energy function. After training the given layer, the weights and activations of the layer are frozen and passed on to the next layer as input.

Assume a CDBN with detection layer ($H$), visible layer ($V$), pooling layer ($P$), and another higher detection layer (${H}^{^{\prime}}$); ${H}^{^{\prime}}$ and ${K}^{^{\prime}}$ has groups, shared weights $\Gamma =\{{\Gamma }^{\mathrm{1,1}}\dots {\Gamma }^{k,{k}^{^{\prime}}}\}$ connects pooling unit ${P}^{k}$ and detection unit ${H}^{l}$. The energy function can be described as (Lee et al. 2009):

$$E\left( {v,h,p,h^{\prime}} \right) = - \mathop \sum \limits_{k} v \circ \left( {W^{k} *h^{k} } \right) - \mathop \sum \limits_{k} b_{k} \mathop \sum \limits_{ij} h_{ij}^{k} - \mathop \sum \limits_{k,l} p^{k} \circ \left( {\Gamma^{kl} *h^{^{\prime}l} } \right) - \mathop \sum \limits_{l} b^{\prime}_{l} \mathop \sum \limits_{ij} h_{ij}^{^{\prime}l}$$

(31)

Based on CNN structure, Wu et al. (2018) presented a novel technique for pathological voice detection, in which the weights of the CNN are pre-trained by a CDBN. The model uses statistical approaches to detect the structure of the input data. The performance of the proposed technique was compared with the existing techniques using the Saarbrucken voice database. Generative models are generally used to develop the deep learning models on a small dataset and avoid overfitting. The study reported an accuracy of 68% and 71% on the validation set, respectively. This is a slight improvement compared to other existing methods. The results demonstrated that CNN can be tuned more robustly by applying CDBN to initiate the weights and can avoid the overfitting issue. However, the accuracy for the testing set decreased, which proves that a more robust system might affect the accuracy.

A Gaussian Bernoulli-based CDBN (GCDBN) model is made up of many coevolutionary layers that are built on Gaussian Bernoulli restricted Boltzmann machines (GBRBM). Therefore, the architecture takes the benefit of GBRBM and convolution neural networks. After each convolutional layer, the feature maps are down-sampled using a stochastic pooling layer. Using a convolutional neural network and GRBM, the proposed system can extract relevant features from a real-sized image using generative convolution filters, reducing the amount of connecting weights, and improving the learning of spatial information from nearby picture patches. Li et al. (2019a, b, c, d) proposed the GCDBN model for image feature extraction, which can reduce the computational cost significantly by replacing fully connected weights with the convolutional filter. However, as a limitation of this study, only one GCDBN was built with five layers. The recognition accuracy can be increased by adding more convolutional and pooling layers in the proposed architecture.

DBNs are also widely used in the analysis of hyperspectral imaging (HSI). However, they fail to examine training samples’ prior knowledge, limiting the discriminant capacity of retrieved features for classification. MMDBN, a manifold-based multi-DBN was thus proposed by Li et al. (2022) in order to acquire deep manifold characteristics of hyperspectral imaging. The MMDBN created a hierarchical initiation approach that initializes the network based on the data's hidden local geometric structure. The MMDBN algorithm efficiently extracted the deep characteristics from each HSI class. Experimental findings on the Salinas, Botswana and Indian Pines datasets reach 90.48%, 97.35%, and 78.25%, respectively, demonstrating that MMDBN outperforms some state-of-the-art algorithms in classification performance. MMDBN’s classification performance can be further improved by designing the combined spectral-spatial deep manifold networks.

4.8 Hybrid neural network

The process of artificial neural network (ANN) learning entails predicting values for a set of parameters and an architecture (Guti 2011). After choosing an architecture, supervised, unsupervised, or reinforcement learning is often accomplished by repetitively modifying the connection weights using a gradient descent-based optimization method. The significant challenges with this type of technique are the need for a prior-determined architecture for the neural net, its sensitivity to early training conditions, and its local nature. Several activations or transfer methods have been used for the hidden layer nodes in hybrid models. Many studies have suggested hybridizing various basis functions via a single hybrid hidden layer or different linked pure layers. A hybrid neural network (HNN) was initially introduced to model a fed-batch bioreactor [36]. The hybrid model is comprised of a partial first principal model that provides previous information about the process with a neural network, which acts as an estimate of unmeasured process arguments.

A genetic algorithm is a type of evolutionary algorithm that uses evolutionary biology concepts like inheritance and mutation. A number of operators (selection operator, substitution operator, recombination operator, and mutation operator) are used in genetic algorithms to bring together the current generation’s eligible members to produce new eligible members. Arabasadi et al. (2017) developed a hybrid technique that combines genetic algorithms with neural networks for diagnosing coronary artery disease, using Gini-index, principal component analysis, information-gain, and weight-by-SVM for feature selection. The initial weights of a neural network were determined with a genetic algorithm, then the neural network was trained using training data. The proposed technique implements a feed-forward topology with one hidden layer in the neural network. The experiment contained 22 inputs and five neurons in a hidden layer to produce an output that indicates whether the patient has CAD or not. The suggested approach improved the performance of a neural network by around 10% by upgrading its initial weights with a genetic algorithm that offers better weights for the neural network. However, several limitations were found in this study. Instead of genetic algorithms, other established evolutionary algorithms like evolution strategy and Particle-Swarm-Optimization (PSO) could be implemented to ensure the validity of the model. Some parameters, such as momentum factor and learning rate, could also be optimized.

A novel metaheuristic method was suggested for improving the free parameters of the PV generation forecasting engine. Using this metaheuristic optimization approach, the shark-smell-optimization (SSO) technique has been enhanced. The metaheuristic algorithm incorporates efficient operators to improve its global and local search capabilities. A new forecasting methodology was applied to a hybrid forecasting engine that combines a neural network with a metaheuristic algorithm (Abedinia, Amjady, and Ghadimi 2018). This method includes a two-stage feature selection filter that filters out inefficient inputs using information-theoretic criteria, such as mutual information and interaction gain. For PV generation prediction, a three-stage neural network-based forecasting engine was designed and trained via a combination of a metaheuristic algorithm and the Levenberg–Marquardt learning method. With the help of this hybrid technique, the neural network-based forecasting engine eliminated underfitting and overfitting problems.

An HNN with Wavelet Transform and Bayesian Optimization was used in a study conducted by (Liu et al. 2022) to predict the copper price for the short-term and long-term. Wavelet Transform was applied to the data to reduce noise and remove extraneous information whereas the algorithm of Bayesian Optimization was utilized on the searching task’s hyperparameter. For training and forecasting copper price, GRU and LSTM were used. The results showed that the proposed approaches, GRU or LSTM, can accurately forecast the copper price in the short and long term with the mean squared errors of less than 3% in both cases. With this HNN, the unnecessary data can be filtered out while the optimal hyperparameter set is searched. It is simple and straightforward to use in predicting the price of other commodities such as the stock market.

4.8.1 Probabilistic neural network (PNN) and two-layered restricted Boltzmann (RBM)

A hybrid deep learning model was presented by Ghosh, Ravi, and Ravi (2016) for sentiment classification that combines a two-layered restricted Boltzmann machine (RBM) and probabilistic neural network (PNN). Sentiment classification is a sub-domain of sentiment analysis that identifies positive and negative sentiments from a review. In the proposed architecture, RBM was used for dimensionality reduction, and PNN classified the sentiment. The hybrid model was assessed in five datasets and performed better than other existing models in this domain. The technique achieved a sensitivity of 92.7%,93.3%, 93.1%, 94.9%, and 93.2% for a book dataset, movie dataset, electronics, and kitchen appliance dataset, respectively. The study revealed that the model does not rely on external resources, such as sentiment dictionaries, reducing the system’s complexity. It also does not perform POS tagging, which, although is typically needed in this domain, reduces the system’s time complexity. In future works, the model should be evaluated with more experiments to ensure its validity.

4.8.2 Dynamic artificial neural network

In the field of deep learning, dynamic neural networks (DNNs) are an emerging technique that can outperform traditional static models in terms of accuracy, adaptiveness, and computational complexity (Han et al. 2021). Static models have limited parameters and computational graphs at the inference stage, whereas DNN architecture and parameters are flexible to different inputs. The outputs of static models are computed based on their link with feed-forward inputs, as there is no feedback. However, the outputs of dynamic neural networks are determined by the present and previous values of inputs, outputs, and the network architecture (Abbas Ali Abounoori Esmaeil Naderi Nadiya Gandali Alikhani Hanieh Mohammadali 2016). DNNs can be divided into three types (Tavarone et al 2018): (i) instance-wise dynamic models that process each instance individually using data-dependent structures or parameters, (ii) spatial-wise dynamic models that perform adaptive computing on image data at various spatial locations, and (iii) temporal-wise dynamic models that accomplish adaptive inference for sequential data, such as movies and texts along the temporal dimension. Instance-wise and spatial-wise methods are used specifically in image recognition, whereas temporal-wise models show emerging improvements in text and audio data. These three types can be combined simultaneously for video-related research domains (Li et al. 2017a, b; Niklaus et al. 2017).

Godarzi et al. (2014) improved an artificial neural network (ANN), specifically named a nonlinear autoregressive model with eXogenous input (NARX), to predict oil prices by developing a dynamic neural network. For the validation and improvements of results, the methodology followed three stages: ANN static, time series, and NARX. For identifying the significant factors that affect the oil price, a time series model was developed in the first stage. Then, a static ANN model was built to verify the acquired data from the first stage to ensure the optimal performance of the NARX model. In the last phase, the NARX model was implemented for the prediction. The methodology was found to be a novel approach for oil price prediction and can be used for other domains like predicting coal or natural gas price.

4.9 Generative adversarial networks

Goodfellow et al. (2014) was the pioneer of adversarial training for image generation, whereby training is formulated as a minimax adversarial game and a discriminator is used to distinguish fake data from real samples. The generator works by generating fake samples based on a probabilistic model with the given data. Then, a classification model is applied to verify whether the generated samples belong to the expected class. The generator aims to fool the discriminator, whereas the discriminator works to detect the false samples generated by the generator. Generative models have been used in a wide range of research domains and have undergone numerous advances since their introduction (Bau et al. 2019; Odena et al. 2017; Brock et al. 2019; Ledig et al. 2017; Miyato et al. 2018; Karras et al. 2018). In every adversarial approach, there are two models working simultaneously: (i) the generative model acquires the data distribution, and (ii) the discriminative model measures the probability of sample point whether it is coming from the training samples. Generative adversarial networks (GAN) learning concerns finding the optimal parameters ${\theta }_{G}^{*}$ for a generator function $G\left(\mathcal{Z}; {\theta }_{G}\right)$ by a minimax game. This relation can be represented by the following expressions (32–35), as suggested by Goodfellow et al. (2014):

$${\theta }_{G}^{*}={}_{{\theta }_{G}}{}^{\mathrm{argmin}} {}_{{\theta }_{D}}{}^{max}f\left({\theta }_{G}, {\theta }_{D}\right)$$

(32)

$$={}_{{\theta }_{G}}{}^{\mathrm{argmin}} f({\theta }_{G},{\theta }_{D}^{*}({\theta }_{G}))$$

(33)

$${\theta }_{D}^{*}\left({\theta }_{G}\right)={}_{{\theta }_{G}}{}^{\mathrm{argmax}} f \left({\theta }_{G}, {\theta }_{D}\right)$$

(34)

where f is determined by:

$$f\left( {\theta_{G} , \theta_{D} } \right) = {\mathbb{E}}_{{x\sim p_{data} }} \left[ {\log \left( {D\left( {\,x; \theta_{D} } \right)} \right)} \right] + {\mathbb{E}}_{{{\mathcal{Z}}\sim {\mathcal{N}}\left( {0,1} \right)}} \left[ {\log (1 - D(G({\mathcal{Z}};\theta_{G} } \right) ; \theta_{D} ))]$$

(35)

For ensuring maximum loss in the above equation, the optimal discriminator ${D}^{*} \left(x\right)$ is a known smooth function for the generator probability ${p}_{G}(x)$, as described in (Goodfellow et al. 2014). The smooth function can be formulated as:

$${D}^{*} \left(x\right)=\frac{{p}_{data} (x)}{{p}_{data} \left(x\right)+{p}_{G}(x)}$$

(36)

GAN has been in a wide range of applications since its emergence. Generative approaches are being applied to validate machine learning models’ robustness and to generate new data for rare examples and for image-to-image translation (Park et al. 2019; Taigman et al. 2017; Xu et al. 2018), image super-resolution (Ledig et al. 2017; Sønderby et al. 2017), synthesis training (Brock et al. 2019; Tang et al. 2019), text-to-image synthesis (Hong et al. 2018; Zhang et al. 2017a, b, c), and many more. However, the training of generative models is very sensitive to the selected hyperparameters. New network architectures have been introduced on a regular basis to this research paradigm in order to maintain training stability.

4.9.1 Unrolled generative adversarial networks

To solve the problems of mode collapse, instability of GANs network training with complex recurrent generators, and increasing diversity, Pfau (2017) introduced a method for reducing complexity in GANs training. The proposed algorithm defines the generator’s objective in order to achieve an unrolled optimization of the discriminator. The authors argued to use a local optimum of the discriminator parameters ${\theta }_{D}^{*}$(as presented in Eq. 34) to be demonstrated as a fixed point, which comes from an iterative optimization procedure. Pfau (2017) developed the complex recurrent generators increasing the diversity and scope of the data distribution. To explain the unrolled GAN, the authors used the discriminator parameter ${\theta }_{D}^{*}$ to express the fixed mark of an iterative optimization process. The expression continues in the following order (15–17):

$${\theta }_{D}^{0}={\theta }_{D}$$

(37)

$$={\theta }_{D}^{k}+{\eta }^{k}\frac{df ({\theta }_{G} ,{ \theta }_{D}^{k})}{d{\theta }_{D}^{K}}$$

(38)

$${\theta }_{D}^{*}\left({\theta }_{G}\right)= \underset{k\to \infty }{\mathrm{lim}}{\theta }_{D}^{k}$$

(39)

where ${\eta }^{k}$ represents the learning rate scheduler. Equation (37) is the full batch steepest gradient ascent equation, and Eqs. (36) and (38) supplement the expression to explain the iterative optimization process. This approach is different from that presented in (Goodfellow et al. 2014), which indicates that the generator requires that the discriminator be updated via several steps to run every update step for the generator. Some drawbacks of this algorithm include high computational cost and cost for each training period as well as increased complexity with respect to the number of steps.

4.9.2 Style-based generator architecture for generative adversarial networks

Motivated by the style-transfer model presented in (Huang and Belongie 2017), an alternative generator architecture was proposed in (Karras et al. 2019) for GANs. The presented generator improved the state-of-the-art work with regard to traditional distribution matrices, which continued towards finding better interpolation properties and latent factors variation. The authors stated that compared to the traditional generators (Karras et al. 2018) that are used to feed the latent code within the input layer, their architecture (Karras et al. 2019) allows input to be mapped through an intermediate space. This latent space then allows control of the generator through the adaptive instance normalization or AdaIN (Dumoulin et al. 2018, 2017; Ghiasi et al. 2017; Huang and Belongie 2017) within every convolutional layer. The proposed automated linear separability and perceptual path metrics quantified the aspects needed for the generator.

The affine transformations learned from the 8-layer MLP was specialized by a parameter w to styles y, where y = (y_s, y_b), which led to AdaIN (Dumoulin et al. 2018, 2017; Ghiasi et al. 2017; Huang and Belongie 2017). Followed by the synthesis network $g$ of each convolution layer, AdaIN function performs the computation as follows:

$${\text{AdaIN}}\,{(}x_{i} ,\,y) = y_{s,i} \frac{{x_{i} - \mu \left( {x_{i} } \right)}}{{\sigma \left( {x_{i} } \right)}} + y_{b,i}$$

(40)

where each feature map ${x}_{i}$ is normalized individually, the feature matrix is scaled, and bias is added by applying the respective scalar components from the style $y$. Karras et al. (2019) redesigned the generator architecture, which exposed new approaches for image synthesis tasks. It is clear from the obtained results that style-based generators outperform the traditional GAN generators.

4.9.3 Multi-Level generative models for partial label learning (MGPLL) with non-random label noise

The presented MGPLL method (Yan and Guo 2020) learns a problem through a feature level and label level generator. It follows a bidirectional mapping of data points and label vectors. A noise label generation is also used while developing the network to form non-random noise and to execute label denoising. The model architecture has a multi-class predictor to locate the training samples to denoise label vectors. Afterwards, a conditional feature generator is applied to perform the inverse mapping. Yan and Guo (2020) adopted adversarial loss from Wasserstein Generative Adversarial Network (WGAN) to formulate their learning. They claimed their model to be the pioneering work that exploited multi-level generative architecture models. Moreover, the network was modelled with non-random noise labels in order to learn the partial label (Zeng et al. 2013). The noise label generator was responsible for exploiting non-random characteristics of noise labels, whereas the data feature generator was accountable for executing the conditioning upon the data samples based on the particular ground data. Later, the prediction model performed inverse mapping between these labels and features. The GAN architecture was designed particularly for label learning partially. The conditional label level generator pointed to the advent of the label-dependent non-random noise, whereas the feature level generator was used to produce data from the denoised label vectors. As a partial label learning generative architecture, the authors tested the model against both synthetic PL and real-world (FG-NET, Lost, MSRCv2, Birdsong, Yahoo! News) datasets, where they achieved satisfactory state-of-the-art performance.

4.9.4 Dual adversarial co-learning for multi-domain text classification

Multi-domain sentiment classification was performed by Wu and Guo (2020) through the novel dual adversarial co-learning method. The authors explored a number of real-world sentiment analysis tasks and demonstrated how multi-domain text classification (MDTC) addresses the problem of a model constructed for one domain failing when tested on another domain. The methodology focuses on domain-invariant and domain-specific features by shared-private networks, and two classifiers were trained to extract features. Both the classifiers and feature extractors were designed to work in an adversarial manner, which resulted in the basis of prediction discrepancy on unlabeled data. A multinomial multi-domain adversarial discriminator was developed to enhance the effectiveness of feature extraction of the domain invariant features. This technique separates the domain-specific features from the domain invariant features. The presented methodology is novel in such a way that the network tries to align data across domains within the extracted feature space and labelled and unlabeled data within each domain. This technique also contributes to avoiding overfitting the limited labelled data.

According to Wu and Guo (2020), if each of the M domains has a limited number of labelled instances, then ${L}_{m}={\{({x}_{i}, {y}_{i})\}}_{i=1}^{{l}_{m}}$ and unlabeled instances ${U}_{m}={\{({x}_{i})\}}_{i=1}^{{u}_{m}}$. In the study, the challenge was to make use of all available resources of the M domains. The authors reported that this helped to improve the multi-domain classification performance. They furthermore introduced separation regularizer (Bousmalis et al. 2016; Liu et al. 2016) to ensure that domain-specific extractors remained distinct from the extractors, which are domain-invariant. The introduced methodology was designed to pull features from domain invariant and domain-specific literature. The shared private network was used to pass the extracted features from the texts, followed by two classifiers that work together in an adversarial fashion. A multinomial multi-domain discriminator was applied to increase the effectiveness of domain-invariant feature extraction. The authors tested this model on two MDTC benchmark datasets and for unsupervised domain adaptability. The generative model positions data with respect to extracted feature space and distinguishes labelled and unlabeled data between each domain. However, the model should be more robust to avoid overfitting for limited data samples.

4.9.5 Capsule neural network

A capsule neural network (CapsNet) was first introduced by Sabour et al. (2017) to address a few drawbacks of the convolutional neural network (CNN). For instance, the sub-sampling layers involved in CNN provide less translation invariance. Also, CNN loses the information about location and position estimation and is more prone to overfitting training data for these reasons. It learns the features without understanding the spatial information. Thus, most of the CNN models are not effective to avoid misclassification. CapsNet addresses these issues by avoiding the sub-sampling layers, which helps the model to maintain the spatial and pose information. The idea of capsules was introduced by Hinton et al. (2011). CapsNets use these “capsule” neural units to encode the relationship between features and location with capsules as well as transformation matrices. Since this approach acquires translation equivariance, CapsNets are more powerful than CNN for samples with misled spatial and pose information.

The dynamic routing algorithm (Sabour et al. 2017) also helps CapsNets to overcome the inability of features to acquire spatial information and scarcity of rotational invariance. CapsNets also encode part-whole relationships like orientations, brightness, and scales among different entities that are objects’ features or feature parts. They use shallow CNN to acquire spatial information. However, CapsNets perform poorly on classification tasks for missing semantic information. For shallow convolutional architecture, a high number of convolutional kernels are used to provide the network with a broad receptive field, but this approach is also prone to overfitting. Since their inception, CapsNets has been employed in various researches, including cancer and tumor cell detection (Mobiny and Van Nguyen 2018; Afshar et al. 2018), generative adversarial network (Jaiswal et al. 2019), monitoring machine health (Zhu et al. 2019), object height classification (Popperli et al. 2019), rice image recognition (Li et al. 2019a, b, c, d), protein translational analysis (Wang et al. 2019), hyperspectral images (Landgrebe 2002), and many more.

Hyperspectral images are used for agriculture (Gevaert et al. 2015), land coverage classification (Yan et al. 2015), vegetation and water resource studies (Govender et al. 2007), scene classification (Hu et al. 2015), and other environmental monitoring related activities. Deng et al. (2018) presented two-layered CapsNet, which was trained on less training samples than Hyperspectral Image (HSI) classification. The work was motivated by the simplicity and comparability of shallower deep networks. The model was trained on two real-life HSI data: PaviaU (PU) and Salins A. Upon the observation, CapsNet gave an overall accuracy of 94% and an average accuracy of 95.90% on the PU dataset, whereas CNN had 93.45% and 95.63% accuracy, respectively. The study also made a comparison among Random Forests, Support Vector Machines, and CNN with CapsNet in terms of network architecture. The authors stated that traditional deep learning-based models would not be suitable for HSI datasets (Zhong et al. 2018) and that CNN could achieve higher performance with more training samples, but for limited training data, CapsNet worked better. Figure 12 shows the native logic for Hyperspectral Image (HSI) classification in its conceptual form.

Fig. 12

HSI classification overview presented in (Deng et al. 2018)

CapsNet was also used in another HSI study (Jiang et al. 2020), in which a new model called Conv-Caps was designed by integrating CNN and a capsule network with Markov Random Fields (MRF) for possessing spectral as well as spatial information. With MRF, the study used graph cut expansion for more efficient classification performance. A CNN-based feature extractor was also used in the network design. In the model, the layer was followed by a feature map in order to obtain a probability map. In the last stage, MRF was used to find subdivision labels. This method takes proper advantage of the spectral and spatial information that hyperspectral images provide. The model was evaluated with a Bayesian framework perspective and produced satisfactory results. To make capsule networks more robust, various research approaches have been introduced over time, a few of which are presented below.

4.9.6 Multi-lane capsule network

Multi-Lane Capsule Network (MLCN) was introduced by Do Rosario et al. (2019) to address the limitation of traditional Capsule Networks. The algorithm was tested on the reputed FashionMNIST and CIFAR10 datasets. When compared to traditional CapsNet architectures, the authors achieved satisfactory outcomes with their novel lane proposals. The experimental baseline was similar to the original configuration employed in (Sabour et al. 2017). According to the findings of do Rosario et al. (2021), MLCN was found to be two times more efficient, on average, than the typical capsule network. The authors introduced the problem of load balancing that occurs when distributing heterogeneous lanes within both homogeneous and heterogeneous accelerators. They addressed this issue with a greedy approach, which was argued to be 50% more efficient than the brute force naive approach. Furthermore, the load balancing issue was handled by the neural architecture search created by their MLCN models, which matched device memory.

Chang and Liu (2020) improved the MLCN algorithm by addressing the issue of capsule networks creating undesirable priorities in the background, which usually results in poor performance if the background contains too much variance. The authors proposed a newly configured multi-lane capsule network architecture with a strict-squash (MLSCN) function for image classification with a complex background to solve this issue. The novel architecture replaced the traditional squash function and optimized the dropout function d. The strict-squash algorithm was proposed to prevent the vulnerability of dynamic routing while also limiting the uselessness of the capsule initialization features. For meaningful feature extraction, the authors also proposed a coherent dynamic weighting assignment strategy in the multi-lane module. By combining these two methods, the authors recommended MLSCN on the basis of MLCN. The research work focused on addressing the issue of misclassification of images with complex backgrounds. This issue can be represented with the input formalized as below (Chang and Liu 2020):

$${G}_{in}^{i\times j}=(({g}_{11}, . ..,{g}_{1j}),({g}_{21},. . .,{g}_{2j}),. . .,({g}_{i1},. . .,{g}_{ij}))$$

(41)

where ${g}_{ij}$ is the input pixel value in location ($i,j$). After the convolutional network processes, the feature map can be obtained using:

$${F}_{out}^{i\times j}=(({\hat{g} }_{11}, . ..,{\hat{g} }_{1j}),({\hat{g} }_{21},. . .,{\hat{g} }_{2j}),. . .,({\hat{g} }_{i1},. . .,{\hat{g} }_{ij}))$$

(42)

where ${\hat{g} }_{ij}$ is the output pixel value in the location ($i,j$); and ${F}_{out}^{i\times j}$ is the capsule layer input, which is responsible to finish the classification step. Following this step, the output layer can be defined as:

$$P=\{{p}_{1} , {p}_{2} , . . . {p}_{j}\}$$

where ${p}_{i}$ is the probability for each category. Most of the regions of an input image have a background as the content or information; however, this information is useless as it is the background of the image. Yet, the capsule network provides redundant attention to the information. As a result, it was identified as the fundamental cause of poor performance in traditional capsule networks. This problem was solved using the aforementioned network combined with the original capsule network along with multi-lane architectures. Chang and Liu (2020) improved their work by making three major contributions: the strict-squash function, lanes filter, and drop-circuit.

If ${u}_{i}$ is activation vector of the capsule i of the previous layer, ${V}_{j|i}$ is the inclination of the capsule $i$ moving to be clustered in capsule $j$. The relation between these two parameters can be formalized by the following equation (Chang and Liu 2020):

$${V}_{j|i}={w}_{j|i}\times {u}_{i}$$

(43)

The summation of coupling coefficients between i and the other previous capsules equals 1, which was achieved by a ‘routing SoftMax’ in which the initial logits ${b}_{ij}$ are prior probabilities and the capsule i must be coupled with capsule j. Equations (44)-(47) are used to perform the necessary computations for the model architecture (Chang and Liu 2020).

$${c}_{ij}=\frac{\mathrm{exp}\left({b}_{ij}\right)}{\sum_{k}{b}_{ik}}$$

(44)

$${s}_{j}=\sum_{i}({c}_{j|i}\times {v}_{j|i})$$

(45)

The squash function is interpreted as a normalization step upon the weighted sum from the previous layers and is presented as:

$${u}_{j}=Squash\left({S}_{j}\right)=\frac{{|\left|{S}_{j}\right||}^{2}}{1+{|\left|{S}_{j}\right||}^{2}}\frac{{S}_{j}}{|\left|{S}_{j}\right||}$$

(46)

Finally, to compute ${c}_{j|i}$ and update ${u}_{i}$ or ${v}_{j|i}$, the following equation is used, where ${u}_{j}$ is the result of the first iteration:

$${b}_{j|i}={b}_{j|i}+{v}_{j|i}\times {u}_{j}$$

(47)

Based on the best classification performance on four benchmark image classification datasets, Chang and Liu (2020) found that, in comparison with a single input type, multiple input types can help the multi-lane architecture to achieve better results. One shortcoming of their research was the drop-circuit, which could not recognize the combined adapted lanes. Consequently, the dropout algorithm would need further research as it establishes randomness in the experimental results.

4.9.7 Complex-valued capsule network (Cv-CapsNet)

To adjust complex datasets, He et al. (2019) focuses on the extraction of multi-scale, complex-valued, and high-level features. Moreover, they introduced an algorithm with a restricted encoding unit of the complex-valued capsule and dense network, with a generalization of the dynamic routing in the complex-valued realm. The generalized dynamic routing algorithm was used to fuse the real- and imaginary values of complex-valued primary capsules. The parameters trained for complex-valued routing were lowered when compared to real-valued routing of the same dimensional capsules. He et al. (2019) also introduced Cv-CapsNet +  + as an extended framework utilizing a 3-level Cv-CapsNet model. It was designed for multi-scale high-level complex-value feature extraction and merging the low-level capsules information that represents the features of instantiation. In addition, Trabelsi et al. (2018) presented a method to simulate complex and real-valued convolution, which was demonstrated for a complex-valued filter matrix $W=\left(A+iB\right)$ and a complex-valued vector $h=(x+iy)$ using the following computation:

$$W*h=\left(A+iB\right)*(x+iy)$$

(48)

Real-valued matrices were also presented to introduce the real and imaginary parts in Eq. (49)

$$\left[\begin{array}{c}\mathfrak{R}(W*h)\\ \mathfrak{I}(W*h)\end{array}\right]=\left[\begin{array}{cc}A& -B\\ B& A\end{array}\right]*\left[\begin{array}{c}x\\ y\end{array}\right]$$

(49)

Here, the real and the imaginary components of the output convolutions are two separate parts. Moreover, the real and the imaginary part for all complex-valued convolutions are detached from each other but concatenated with respect to the real and complex parts for the following complex-part layer. He et al. (2019) argued that this modelling guarantees the sustainability of the complex-valued convolutions and ensures the complex-valued encoding. Thus, the architecture was employed to fetch multi-scale features, including original, semantic, and structure features. In the model, CReLU (complex-valued) (Trabelsi et al. 2018) was chosen as the activation function. The authors implemented the model on CIFAR10 Fashion and MNIST datasets. The model performed well by achieving fewer trainable parameters with a smaller number of iterations. The generalized dynamic routing algorithm helped to combine the real values with the imaginary values, greatly reducing the number of trainable parameters for the same dimensional complex routing model as compared to the real-valued routing models. However, they could not reduce the computational complexity for training the model.

4.9.8 Multi-scale CapsNet

A novel variation of capsule networks was introduced by Xiang et al. (2018), focusing on computational efficacy and representation capacity. In the leading stage of the presented multi-scale architecture, information was extracted following the multi-scale information extraction method. However, on the second stage hierarchy, the features were encoded into multi-dimensional capsules. An improved drop-out was also introduced in the research work to enhance the robustness of the capsule network. The authors considered the hierarchical features of the dataset and exploited multi-dimensional capsules for encoding those features. The multi-scale capsule encoding consists of two stages, where the first stage obtains the semantic and structural information through multi-scale feature acquisition. Another top branch of the two layers retrieved the semantic information from the data as well. The foremost hierarchy of the middle branch of the architecture performed the medium-level feature extraction process. The last branch took on the actual original features that were obtained without trainable parameters. In the second stage of the architecture, feature hierarchies were encoded into multi-dimensional capsules. The final branch layer was encoded to high-level features of 12D, medium level features of 8D and low-level features of 4D. The following weight matrices were used to compute the predicted vectors (Xiang et al. 2018):

$${\hat{u} }_{j|i}^{1}= {W}_{ij}{u}_{i}^{1}$$

$${\hat{u} }_{j|i}^{2}= {V}_{ij}{u}_{i}^{2}$$

$${\hat{u} }_{j|i}^{3}= {U}_{ij}{u}_{i}^{3}$$

$$\hat{u} =concat({\hat{u} }^{1},{\hat{u} }^{2},{\hat{u} }^{3})$$

Equation (50) is used as the objective function of the multi-category capsule network (Xiang et al. 2018):

$${L}_{M}=\sum_{j=1}^{J}{T}_{j}\mathit{max}{\left(0,{m}^{+}-\| {V}_{j}\| \right)}^{2}+ \lambda \left(1-{T}_{j}\right)max{(0,\Vert {V}_{j}\Vert -{m}^{-})}^{2}$$

(50)

The length of a capsule portrays the probability of the entity, where the length is argued to be compressed to [0,1]. Equation (51) represents that the length can be compressed without changing its direction and helps in translating the length as the capsule detects the actual probability of a given data feature:

$${v}_{j}=\frac{{\| {s}_{j}\| }^{2}}{1+{\| {s}_{j}\| }^{2}}\frac{{s}_{j}}{\| {s}_{j}\| }$$

(51)

where ${v}_{j}$ represents the capsule output of the j-th unit; and ${s}_{j}$ is the total input. Dynamic routing was used as a form of the information selection method, which ensures that the outputs of the children capsules are sent to their respective parent capsules (Xiang et al. 2018). On the other side, the routing coefficients are adjusted by the update() function shown below:

$${b}^{i+1}={b}^{i}+{\hat{u} }_{j}\cdot {u}_{j}$$

$${c}^{i+1}=softmax({b}^{i+1})$$

The authors achieved state-of-the-art performance of the model on FashionMNIST and CIFAR10 datasets. MS-CapsNet was also used in the Synthetic Aperture Radar (SAR) image detection task (Xiang et al. 2018). Gao et al. (2021) addressed the issue of noise detection and deformation sensing in traditional CNN architectures with their implemented multiscale capsule network for feature extraction in SAR image pixels. The multiscale module exploited spatial information from the image features. The authors also applied an adaptive fusion convolution module to address the issue of noise detection and tested the model's architecture on three real-life SAR datasets.

4.9.9 Attention mechanism

The attention mechanism is described as a mapping mechanism to query and set a key-value pair to the output. In the output, all of the elements in values, keys, query, and output are vectors. The output values are produced as a weighted sum of the input values, and the weight values are assigned using a compatibility function. The query with respect to the associated key generates this compatibility function. Self-attention, also known as intra-attention, is such an attention-based mechanism that relates various positions of a unit sequence to compute the representation of that sequence input. The self-attention algorithm has been used for reading comprehension (Cheng et al. 2016), textual entailment (Paulus et al. 2018), summarization (Parikh et al. 2016), task-dependent sentence representation (Lin et al. 2017), and in many other fields.

Vaswani (2017) introduced the transformer-based attention mechanism for sequence transduction, replacing the recurrent units to employ in encoder-decoder network architectures for multi-headed self-attention units. The transformer was trained significantly for translation tasks and was found to be faster than the recurrent and convolutional-based architectures. The model was applied to 2014 WMT English-to-German and 2014 WMT English-to-French machine translation work. The encoder was used to map and input sequence for symbol representations and to generate an output sequence given the continuous representation. The transformer was employed to follow the overall architecture with the help of self-attention as well as the point-wise fully connected layers within the encoder-decoder network architecture.

Vaswani (2017) proposed a self-attention algorithm to perform two machine translation work and achieved satisfactory and parallelizable results. The model obtained a 28.4 score on BLEU for the 2014 WMT English-German machine translation task and a 41.8 score on the 2014 WMT English-French machine translation work. The model was generalized through the transformer-based attention mechanism on words, which proved to be advantageous over previous researches (Gehring et al. 2017; Kaiser and Sutskever 2016). It was successfully implemented to the English constituency parsing task with both large and limited training samples. However, the authors did not evaluate this model for image, audio, and video data.

4.9.10 Deep Boltzmann machines

Deep Boltzmann Machine (DBM) (Srivastava and Salakhutdinov 2014), a deep neural network architecture, is trained in a semi-supervised approach. The architecture of DBM allows the network to acquire knowledge about complex feature-based relationships. DBMs have a wide range of applications like facial expression recognition (He et al. 2013), text recognition (Srivastava and Salakhutdinov 2014), person identification from audio-visual data (Alam et al. 2017), 3D model recognition (Leng et al. 2015), and many more. DBM consists of units that are respective to input data. The hidden units in a DBM consist of symmetrical-coupled stochastic binary units. Different layers of the DBM architecture hold the binary hidden units. Coupling is enabled in consecutive two layers in a top-down and bottom-up approach. Such structure allows DBM to understand complicated internal representations of input data.

4.9.11 Deep-FS: A feature selection algorithm for deep Boltzmann machines

A deep feature selection algorithm was presented by Taherkhani et al. (2018), which was argued to have the ability to remove unwanted features from extensively large datasets. Considering that a feature selection algorithm can help improve the performance of a machine learning model significantly, this algorithm was developed for DBM domain work. The algorithm was used by a Deep Boltzmann Machine and gathered the data distribution in a network. Such an algorithm is capable of embedding feature selection within a Restricted Boltzmann Machine, as presented in Fig. 13.

Fig. 13

Representation of a restricted Boltzmann machine comprised of two layers of hidden and visible neurons. In the network, there are D visible and F hidden neural units (Taherkhani et al. 2018)

Considering an RBM of D binary units, if V is a vector containing states of the D units, there is the set V $\in$ {0,1}^D and a vector h, which contains states of the hidden units. If an RBM has F hidden neurons, the F dimensional hidden variables are h $\in$ {0,1}^F. Taherkhani et al. (2018) expressed the joint configuration of V and h as defined in the following Eq. (52):

$$E\left(\mathbf{V},{\varvec{h}}\right)=-\sum_{i=1}^{D}\sum_{j=1}^{F}{W}_{ij}{v}_{i}{h}_{j}-\sum_{i=1}^{D}{b}_{i}{v}_{i}-\sum_{j=1}^{F}{a}_{j}{h}_{j}$$

(52)

where ${W}_{ij}$ is the weight connecting the ith visible component ${v}_{i}$ and the jth hidden component ${h}_{j}$; and ${b}_{i}$ and ${a}_{j}$ are the biases connecting to the ith visible units and the jth hidden units, respectively. An energy function was employed by Taherkhani et al. (2018) for the joint distribution of the visible and hidden variables, which assignment is demonstrated in Eq. (53):

$${\varvec{P}}\left(\mathbf{V},{\varvec{h}}\right)=\frac{1}{{\varvec{Z}}}\mathrm{exp}\left(-{\varvec{E}}\left(\mathbf{V},{\varvec{h}}\right)\right)$$

(53)

where ${\varvec{Z}}$ is a partition function, also known as the normalizing term. The function ${\varvec{Z}}$ is defined below:

$${\varvec{Z}}=\sum_{{\varvec{V}}}\sum_{{\varvec{h}}}\mathrm{exp}(-{\varvec{E}}(\mathbf{V},{\varvec{h}}))$$

(54)

The overall sum was calculated for all pairs (V,h). If V is a D dimensional vector and h is an F dimensional binary vector, there are 2^D+F different pairs of (V,h) that are possible. Additionally, the visible units are considered to be binary. Moreover, the conditional probabilities of $P\left({\varvec{h}}|{\varvec{V}}\right)$ and $P\left({\varvec{V}}|{\varvec{h}}\right)$ were calculated in (Taherkhani et al. 2018) by the following equations:

$$P\left({\varvec{h}}|{\varvec{V}}\right)=\prod_{j=1}^{F}p\left({h}_{j}|{\varvec{V}}\right)$$

(55)

$$P\left({\varvec{V}}|{\varvec{h}}\right)=\prod_{i=1}^{D}p\left({v}_{i}|{\varvec{h}}\right)$$

(56)

Furthermore, these conditional probabilities can be extended as:

$$\mathrm{p}\left({h}_{j}=1|\mathbf{V}\right)=\mathrm{g}(\sum_{i=1}^{D}{W}_{ij}{v}_{i}+{a}_{j})$$

(57)

$$\mathrm{p}\left({v}_{i}=1|\mathbf{h}\right)=\mathrm{g}(\sum_{j=1}^{F}{W}_{ij}{h}_{j}+{b}_{i})$$

(58)

Based on the results of Taherkhani et al. (2018), the novel feature selection algorithm was designed to handle feature selection from large datasets. The algorithm was embedded into DBM classifiers, which helped to handle a reduced quantity of input features with less learning errors from large datasets. The algorithm performed well because of its ability to remove irrelevant features from large data. The results demonstrated that more than 45% of the features can be reduced from the FashionMNIST dataset, which helped to reduce the network error from 0.97 to 0.90%. In addition, the time of execution was reduced by more than 5.5% for classification tasks. The model was tested on GISETTE, PANCAN, and MADELON datasets and showed to be highly effective for all datasets. Specifically, it reduced the input features by 81% for GISETTE, 77% for PANCAN, and 57% for MADELON datasets.

4.9.12 Restricted Boltzmann machine

Restricted Boltzmann machine (RBM) is a variant of the Boltzmann Machine, containing a stochastic neural network (generally) for unsupervised learning (Guo et al. 2016). Unlike other Boltzmann machines, RBMs have a defining trait of providing a bipartite graph for its visible and hidden layers, enabling the implementation of a gradient-based contrastive divergence algorithm for training. Developed RBM models use noisy rectified units (linear) to store data on intensities. To create learning modules, RBMs can be efficiently applied to compose deep networking models, such as Deep Energy Models (DBNs), Deep Boltzmann Machines (DBMs), and Deep Belief Networks (DBNs). Generally, RBMs are not a popular choice for computer vision-based applications; however, in recent times, a few RBM models have been structured to perform vision tasks. For example, Shape Boltzmann Machine, proposed by Eslami et al. (2014), can learn to apply the probability distribution method on object shapes to model binary shape images.

Another prominent use of RBMs, suggested by Kae et al. (2013), is in combination with CRF to model local and global structures for face segmentation with improved performance in face labelling. Furthermore, another novel method based on DBN architecture and mean-covariance RBM was employed for phone recognition. Various frameworks and models for RBMs have been intensively studied and developed, each having its own sets of merits and demerits. Although most RBMs that are utilized for vision tasks exhibit remarkable capability in performing image and object classification/identifying tasks, such models must be a hybrid of one or more networks to be efficient. As of yet, standard RBMs alone are not adopted for memory associative or computer vision-based tasks and are usually in compliance with more than one other deep learning framework.

4.9.13 Sequence classification restricted Boltzmann machines with gated units

The intractability of learning and inference in RBM was investigated by Tran et al. (2020) considering the exponential complexity of the gradient computation while maximizing the log-likelihoods. The algorithm optimized a conditional probability distribution in place of a joint probability distribution for sequence classification. The authors also introduced gated-Sequence Classification Restricted Boltzmann Machine (gSCRBM), in which an information processing gate is integrated alongside long short-term memory (LSTM) networks. The network architecture was evaluated in an optical character recognition (OCR) task and for multi-resident activity recognition in smart homes. It was argued that gSCRBM requires much fewer parameters compared to other recurrent architectures with memory gates. The SCRBM was constructed by the rolling RBMs along with the class label over the time of training. The network architecture interpreted the probability distribution with the following equation:

$$p\left( {y^{1:T} ,x^{1:T} ,h^{1:T} } \right) = \mathop \prod \limits_{t = 1}^{T} p(y^{t} ,x^{t} ,h^{t} |h^{t - 1} )$$

(59)

where ${\mathbf{x}}^{1:T}$, ${\mathbf{h}}^{1:T}$ are the time series corresponding to the visible and hidden states; ${y}^{1:T}$ is a sequence of class labels; and ${\mathbf{h}}^{0}$ are the hidden unit biases.

The model faced difficulty with an intractable inference, as explained in (Sutskever and Hinton 2007). The authors also suggested that this problem could be solved through the addition of recurrent units, as done for RTRBM (Sutskever et al. 2009). For RTRBM, the class labels were excluded, while in the case of SCRBMs, local distribution at time t was p(${y}^{t} ,{\mathbf{x}}^{t} ,{\mathbf{h}}^{t}|{\mathbf{h}}^{t-1})$. This was replaced by the expression presented in Eq. (60):

$$p({y}^{t} ,{\mathbf{x}}^{t} ,{\mathbf{h}}^{t}\left|{\hat{\mathbf{h}}}^{t-1}\right)=\frac{\mathrm{exp}(-{E}_{\theta }({y}^{t} ,{\mathbf{x}}^{t} ,{\mathbf{h}}^{t};{\hat{\mathbf{h}}}^{t-1})}{{\sum }_{{y}^{t} ,{\mathbf{x}}^{t} ,{\mathbf{h}}^{t}}\mathrm{exp}(-{E}_{\theta }({y}^{^{\prime}} ,{\mathbf{x}}^{^{\prime}} ,{\mathbf{h}}^{^{\prime}};{\hat{\mathbf{h}}}^{t-1})}$$

(60)

where ${\hat{\mathbf{h}}}^{t-1}$ is the expected values vector for the hidden units at time t-1 and is calculated as:

$${\hat{\mathbf{h}}}^{t-1}={\mathbb{E}}[{\mathbf{H}}^{t-1}|{\mathbf{x}}^{1:t-1}, {y}^{1:t-1}]$$

(61)

The local energy function is given by:

$${E}_{\theta }\left({y}^{^{\prime}} ,{\mathbf{x}}^{^{\prime}} ,{\mathbf{h}}^{^{\prime}};{\hat{\mathbf{h}}}^{{\varvec{t}}-1}\right)=-\left[{\left({\mathbf{x}}^{t}\right)}^{\mathrm{\top }}{\mathbf{W}}_{xh}+{\mathbf{u}}_{{{\varvec{y}}}^{{\varvec{t}}}}^{\boldsymbol{\top }}+{\left({\hat{\mathbf{h}}}^{{\varvec{t}}-1}\right)}^{\boldsymbol{\top }}{\mathbf{W}}_{hh}\right]{\mathbf{h}}^{t}-{\mathbf{a}}^{\top }{\mathbf{x}}^{t}-{b}_{{y}^{t}}-{\mathbf{c}}^{\top }{\mathbf{h}}^{t}$$

(62)

The algorithm was designed to achieve better learning and dynamic interference in sequence classification. For long-term information retrieval, the algorithm followed the structure of rolling RBMs, and gated units (gSCRBM) were introduced. The gSCRBM performed better in terms of parameters because it was trained with fewer parameters than traditional LSTMs and GRUs. The model was evaluated to prove its superior performance over advanced LSTM structures (Yu et al. 2019), Bidirectional LSTM (BiLSTM), and Stacked LSTM (StackedLSTM) (Graves and Schmidhuber 2005). It was found that SCRBM outperformed the other models in terms of generalization. Although GRUs and LSTMs generated better results in a few circumstances, the authors explained that those architectures demand more sophisticated structures, longer processing time, and more hidden units. SCRBM was found to be more compact with fewer parameters but with the same amount of neurons as another RNN network containing the same hyperparameters. However, the SCRBM was not able to capture long-term information, which led to a vanishing gradient or exploding gradient problem. This issue was later resolved by the gated unit (gSCRBM).

4.10 Stacked denoising autoencoders

4.11 Autoencoders

Autoencoder neural networks were designed for unsupervised learning by applying a backpropagation algorithm of the target values for equalizing the inputs. The autoencoder learns the approximation between the output and identity function when the input is compared to the output. When the autoencoder discovers the features or data structure, the hidden units are subjected to a sparsity constraint. Autoencoder models require knowledge of the geometry of the data to properly understand the input data. Constraining the node in the hidden layer allows autoencoders to learn the low-dimensional representation of the model.

4.11.1 Autoencoders for Words

Liou et al. (2014) presented the Elman network for encoding each word of a different vector in semantic space, which is related to corresponding entropy coding (Elman 1990, 1998) and is operated on an encoder for training. The authors utilized the Elman network as a super Turing machine for powerful computation work (Siegelmann 1995). Figure 14 illustrates the Elman network employed by a simple recurrent network, which was designed for semantic word categorization. However, because it could not handle the encoding task, the Elman network was redesigned in order to encode the words into the semantic space domain. The achieved codes were utilized in indexing, ranking, and categorizing literary tasks.

Fig. 14

Representation of Elman network (Liou et al. 2014)

Liou et al. (2014) encoded each word for individual vectors while training. The ward was bound with corresponding entropy coding in semantic space. The training methodology also included ranking, indexing and categorizing literacy steps from the training data. The model was trained on the basis of acquired datasets from two Chinese novels: Romance of the Three Kingdom and Dream of the Red Chamber. However, they still needed to investigate whether a low error rate could be achieved without the renewed coding units and the same network architecture.

4.11.2 Deep energy models

The deep energy model (DEM) is a deep learning training technique for deep networks and architects based on the restrictive Boltzmann machine learning methodology (I. Goodfellow et al. 2016; Guo et al. 2016). It includes a feed-forward neural network that transforms data inputs deterministically rather than modelling the output via a layer of stochastic hidden units (perceptron/neuron), as shown in Fig. 15. The feedforward network $({g}_{\theta })$ acts on the universal approximation theorem in order to approximate a continuous function, mapping corresponding inputs and outputs (Nguyen-Thanh et al. 2020).

Fig. 15

Schematic representation of deep energy model (Samaniego et al. 2020)

Unlike deep belief networks and deep Boltzmann machines that have multiple stochastic hidden layers, DEM consists of a single stochastic hidden layer (h), which allows efficient inference and simultaneous training of all the layers within the network (Ngiam et al. 2011). Hopfield energy models were one of the earlier developed DEMs that, in their simplistic nature, allow closed-form modelling (Bartunov et al. 2019). However, the Hopfield model has significant demerits and is unable to work with the quadratic dimensionality of memory patterns. The capacity for more patterns is also limited by the number of parameters in the network. Since real-world data consist of higher-order dependencies, the Hopfield energy model cannot be used (Bartunov et al. 2019). Ngiam et al. (2011) utilized the DEM approach to process natural images, demonstrating significant improvements in data outputs when compared to greedy layer-wise training. In recent years, the development of energy-based models meta-learning (EBMM) has been observed to show better performance as a memory model that is capable of recalling training, memorizing patterns, and performing compression (Bartunov et al. 2019; Kraska et al. 2018; Parkhi et al. 2015; Sun et al. 2015; Zhang et al. 2016a, b). Meta-based learning primarily operates on the read (x$;\uptheta$) and write (X) functions by means of truncated gradient descent, as follows:

$$read\,(\tilde{x};\,\theta )\, = \,x^{{\left( {K + 1} \right)}} = x^{k} - \gamma^{ \left( k \right)} \nabla_{x} E\left( {x^{\left( k \right)} } \right),\,x^{(0)} = \tilde{x}$$

(63)

$${\text{L}}\left( {{\text{X}}, \theta } \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} E[|\left| {x_{i} - {\text{read}}\left( {\overline{{x_{i} }} ;\theta } \right)} \right||_{2}^{2} ]$$

(64)

$$\mathrm{W}(\mathrm{x},\uptheta ) =\mathrm{ E}(\mathrm{x};\uptheta ) +\mathrm{ \alpha }|\left|{\nabla }_{\mathrm{x}}\mathrm{E}\left(\mathrm{x};\uptheta \right)\right|{|}_{2}^{2}+\upbeta ||\uptheta - \overline{\uptheta }|{|}_{2}^{2}$$

(65)

$${\text{write}}\,(X)\,\theta^{(T)} ,\,\theta^{{\left( {t + 1} \right)}} = \theta^{\left( t \right)} - \eta^{\left( t \right)} \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \nabla_{\theta } W(x_{i, } \theta^{\left( t \right)} ),\,\theta^{(0)} = \overline{\theta }\,$$

(66)

where $\mathrm{x}$ is the input (the deterministic dynamics); X represents the Nth set of input patterns compressed into parameters,$\uptheta$, by the writing rule; N is the number of stored patterns; k = 1, 2,…K (number of sequences required to be updated to perform gradient descent for optimization for reading function); t = 1, 2,…T (number of sequences required to be updated to perform gradient descent for optimization for write function), respectively; ${\upgamma }^{ \left(\mathrm{k}\right)}\mathrm{ and }{\upeta }^{(\mathrm{t})}$ are the learned stepped sizes for reading and writing functions respectively; $\mathrm{E}\left(\mathrm{x}\right)$ represents the energy function; ${\nabla }_{\mathrm{x}}$ is the derivative operator; and $\mathrm{W}\left(\mathrm{x},\uptheta \right)$ is the writing loss function, consisting of meta parameters $\mathrm{\alpha }$ and$\upbeta$, representing the energy function at a local minimum that must be two-fold and requires the hessian term to be positive. The later part of the writing loss function performs optimization, limiting deviation of prior parameter, $\overline{\uptheta }$, from the initial parameter,$\uptheta$. Finally, implementing gradient descent tunes the writing function as Eq. (34); where $\mathrm{L}\left(\mathrm{X},\uptheta \right)$ denotes the score matching objective, or the reconstruction error for the read function.

Compared to past DEMs, EBMMs can utilize slow gradient learning, having effective convolutional memories, particularly due to fast writing rules (Bartunov et al. 2019). EBMMs also adhere to and manage memory capacity efficiently, even for non-compressible inputs, such as binary strings to natural images of high compression. It also has the ability to differentiate different patterns (energy levels). The method proposed by Bartunov et al. (2019) resolves the functioning pace of EBMMs with fast writing and limited parameter updates (a maximum of 5 steps), adding new inputs for the weights. Another advantage of this method is the association of faster reading and fewer gradient descent steps. The employability of the proposed operations, which store N patterns in memory and do not require additional assumptions, further adds to the efficiency of the model (Bartunov et al. 2019). However, batch writing assumption is a challenge for EBMM and could be improved with more elaborate architecture.

It is also difficult to find the optimum balance between writing speed and the model’s capacity (a commonality for most deep learning energy models) (Ba et al. 2016; Bartunov et al. 2019). In addition, the characterized properties of the learning attractor models are not yet known, and EBMM cannot return different associations when under uncertainty, which occurs due to compression. Furthermore, with the general application of gradient-based meta-learning, it is difficult to evaluate the expected outcome of EBMMs, mainly because of the high dimensionality pattern space of inputs that increases the resulting distortion of the model and decreases the output reliability after adaptation. Therefore, a different gradient descent functionality is necessary. Also, parametric gradient-based optimization requires significant updates (for memory/recalling applications) and, hence, is slow. Resolving these existing issues, together with the observation and exploration of more stochastic variants for EBMMs would lead to significant improvements for DEM.

Statistical learning and construction of an inference-free hierarchical framework offer a viable solution for density estimation, consisting of higher dimensional challenges. By utilizing Bayesian (Eq. (67)) and Parzen score matching functions (Eq. (68)) (Saremi et al. 2018; Vincent 2011) together with a multilayer perceptron of scalable energy learning operation (Eq. (69)), the deep energy estimator network (DEEN) can be modelled and further optimized (Saremi et al. 2018), as follows:

$$\widehat{\mathrm{x}}\left(\upxi \right)=\upxi +\upsigma 2\uppsi (\upxi ;\uptheta )$$

(67)

where σ denotes any level of noise; ψ represents the score function; ξ is the noisy measurement of underlying random variable x; and $\uptheta$ is the parameter vector.

$$\mathrm{P}\left(\upxi \right)=\frac{1}{\mathrm{n}}\sum_{\mathrm{k}}\mathrm{S}(\upxi |{\mathrm{x}}^{\left(\mathrm{k}\right)})$$

(68)

where P represents the Parzen density estimator; S signifies the smoothing kernel; k represents the nth x of a dataset, x = {${\mathrm{x}}^{1}, {\mathrm{x}}^{2}\dots {\mathrm{x}}^{\mathrm{n}}$}; and n is the number of elements in the dataset, x.

$$\mathrm{E}\left(\mathrm{x};\uptheta \right)= \sum_{\mathrm{\alpha }}{\mathrm{w}}_{\mathrm{\alpha }}^{(\mathrm{L}+1)}{\mathrm{h}}_{\mathrm{\alpha }}^{\left(\mathrm{L}\right)}\left(\mathrm{x};\left\{{\mathrm{w}}^{\left(1\right)}, {\mathrm{w}}^{\left(2\right)}, \dots , {\mathrm{w}}^{\left(\mathrm{L}\right)}\right\}\right)=\sum_{\mathrm{\alpha }}{\upvarepsilon }^{\mathrm{\alpha }}(\mathrm{x};\uptheta )$$

(69)

In Eq. (69) (Saremi et al. 2018), $\mathrm{E}\left(\mathrm{x};\uptheta \right)$ is linearly constructed from the preceding hidden layer h^L, in which w is the weight of each data x and parameter $\uptheta$, ${\upvarepsilon }^{\mathrm{\alpha }}$ denotes the expert (corresponding products of expert, PoE) parametrized by the neural network, and α signifies the number of iterations.

Deep energy estimator networks (DEENs) have been demonstrated to be effective with high dimensionality data values (Saremi et al. 2018). However, it is important to note that although DEEN can auto-regularize due to its Parzen function, it is not an autoencoder. In fact, DEEN can operate with a decoder by not directly estimating the score functions (Alain et al. 2014) and, thus, skipping stability issues of denoising autoencoders. Being dataset-dependent, DEEN does not impose any bounds towards σ and can be effectively regularized. Apart from working with higher dimensionality data, deep energy estimators are employed for semi-supervised, unsupervised learning, and generative modelling (Saremi et al. 2018). DEENs provide consistent estimations and, therefore, acquire increasing interest; however, more testing is required to examine the network’s performance for dynamic data as well as the scalability potential.

Another prominent application of DEM is the nonlinear finite deformation hyper-elasticity problem, operating on an energy and loss function. For instance, using Eulerian motion description and transport deformation gradient formulation, the nonlinear response of elastic materials (in 3D) with a large deformation continuum can be modelled by employing DEM via DNNs. In a previous work, a neural network is structured using Eq. (70), then optimized to minimize its potential energy using a loss function (Nguyen-Thanh et al. 2020):

$${\hat{\text{z}}}_{{\text{k}}}^{{\text{l}}} = {\upsigma }\left( {\mathop \sum \limits_{{{\text{j}} = 1}}^{{{\text{n}}_{{{\text{l}} - 1}} }} {\text{w}}_{{{\text{kj}}}}^{{\text{l}}} {\hat{\text{z}}}_{{\text{k}}}^{{{\text{l}} - 1}} + {\text{ b}}_{{\text{k}}}^{{\text{l}}} } \right),\,0\, < 1 < {\text{L}}\,{\text{(the final layer)}}$$

(70)

where $\widehat{\mathrm{z}}$ is the final output of the final layer l; w and b are weights and biases, respectively; and $\upsigma$ is the activation function acting on the kth neuron of the lth layer.

DEM can also be utilized for nonlinear deformation, being faster with fewer coding and having the traction-free boundary conditions to be auto-filled. Training enables faster solution retrieval, and the model can be easily coded in common machine learning operating platforms, such as TensorFlow and Pytorch (Nguyen-Thanh et al. 2020). However, the use of DEM has certain drawbacks due to the imposition of the boundary condition of parameters and the associated integrations used for modelling and, therefore, requires further study to improve the integration techniques. Moreover, the modelling tends towards non-convexity of loss function during the nonlinear evolution of network neurons, and so, an enhanced theoretical understanding is required to better establish the deep neural network architecture. DNNs for finite deformation hyper-elasticity are trained using backpropagation, computing the gradient loss and minimizing the function, using a standard optimizer. Considering the tendency of a gap to exist between backpropagation and energy-based models, Nguyen-Thanh et al. (2020) administered forward propagation to approximate the solution with defined boundary conditions, which directs the prediction. Scellier and Bengio (2017) proposed equilibrium propagation to bridge gaps between backpropagation and the energy-based model. The main objective of equilibrium propagation is to ensure a learning framework for the DEMs with a 0.00% training error. Provided the statistics of an excellent training error score, it would be interesting to observe the performance of such a system for different deep learning techniques and DEMs with complex non-linear data of high parameters and dimensions.

Reinforcement learning (RL) is another intensively studied deep learning method that has unique connections with DEMs in terms of state and action spaces. RL surpluses the shortcomings associated with DEMs, which are mostly sampling issues and unpopularity with regression models (Zhang et al. 2020). For example, performing molecular modelling using a DEM-based system would be difficult due to the absence of frameworks that do not involve a classification route for the dataset. Consequently, when it comes to modelling problems that do not involve density estimations or the necessity for energy functions, a new neural network is required. Recently, Zhang et al. (2020) proposed a novel approach, where RL is reformulated into distribution learning to resolve sampling issues, using a minimax generative adversarial network to develop a targeted adversarial learning optimized sampling (TALOS) methodology. Another technique using entropy policy, called variational adversarial density estimation (VADE), was also effective (for molecular modelling), demonstrating how cross-fertilization between EBMs/DEMs and RL can overcome the challenges of EBMs. Haarnoja et al. (2017) explored maximum RL via DEM using the Markov decision process (Eq. (71)) and modified the objective to maximize the entropy (Eq. (72)). Using soft Q learning and the Bellman equation, the model operated on learning maximum entropy policies (Eq. (73)).

$${\uppi }_{\mathrm{std}= }{\mathrm{argmax}}_{\uppi }\sum_{\mathrm{t}}{\mathrm{E}}_{{(\mathrm{s}}_{\mathrm{t}+{\mathrm{a}}_{\mathrm{t}}})\sim {\mathrm{p}}_{\uppi }}[\mathrm{r}({\mathrm{s}}_{\mathrm{t}}, {\mathrm{a}}_{\mathrm{t}})]$$

(71)

$${\uppi }_{\mathrm{MaxEnt}= }{\mathrm{argmax}}_{\uppi }\sum_{\mathrm{t}}{\mathrm{E}}_{{(\mathrm{s}}_{\mathrm{t}+{\mathrm{a}}_{\mathrm{t}}})\sim {\mathrm{p}}_{\uppi }}[\mathrm{r}({\mathrm{s}}_{\mathrm{t}}, {\mathrm{a}}_{\mathrm{t}})]+\mathrm{\alpha H}(\uppi (\cdot |\mathrm{st}))]$$

(72)

where S and a are state and action space, respectively; r denotes reward; ${p}_{\pi }$ signifies the marginals of state and state action for the policy, $\uppi (\cdot |\mathrm{st})$; and $\mathrm{\alpha }$ acts as a hyperparameter.

$${\uppi }_{\mathrm{MaxEnt }}\left(\mathrm{at}|\mathrm{st}\right)=\mathrm{exp}\frac{1}{\mathrm{\alpha }}({\mathrm{Q}}_{\mathrm{soft}}^{*}\left({\mathrm{S}}_{\mathrm{t}}, {\mathrm{a}}_{\mathrm{t}}\right)-{\mathrm{V}}_{\mathrm{soft}}^{*}(\mathrm{st})))$$

(73)

where ${\mathrm{V}}_{\mathrm{soft}}^{*}$ represents a partition log function; and ${\mathrm{Q}}_{\mathrm{soft}}^{*}$ denotes a Q-function (proven and detailed by Ziebart and Fox (2010) and Haarnoja et al. (2017), respectively).

Reinforcement learning energy modelling policies, which are suitable for high-dimensional values, have been observed to be robust and applicable to code robotic tasks and, hence, have become quite popular amid humanoid robots. Although the model requires pre-training of the general-purpose stochastic policies, when compared with other deep energy modelling techniques, reinforcement learning via DEM seems most promising, particularly by being able to solve inputs and sampling issues for energy-based modellings.

4.11.3 Deep coding network

Deep predictive coding network is a bio-inspired framework built on the theoretical understanding of how the brain infers sensory stimuli. The mechanism by which the brain speculates decisions based on certain data (e.g. visual information) has been formulated as the baseline for predictive coding, followed by the adaptation of filter objectives and training of modules via gradient descent. However, due to the still very misunderstood functioning of neurons in the brain, it is likely that the connected neurons in the brain consist of a more complex architecture, significantly limiting existing deep learning models. Incorporating a feedforward and feedback (prediction making) system along with each layer of a neural network is a generative understanding of deep coding networks, particularly the deep predictive coding system. Such networks are heavily studied and used for computer vision, where classification for images and videos is performed.

A base equation for a deep predictive coding network is given by (Dora et al. 2018):

$$\mathrm{E}= \sum_{\mathrm{l}=0}^{\mathrm{N}}(\sum_{\mathrm{m},\mathrm{n}}^{{\mathrm{Y}}_{1}, {\mathrm{X}}_{1}}{\mathrm{l}}_{\mathrm{p}}\left({\mathrm{y}}_{\mathrm{m},\mathrm{n}}^{\mathrm{l}}-{\widehat{\mathrm{y}}}_{\mathrm{m},\mathrm{n}}^{\mathrm{l}}\right)+ \sum_{\mathrm{m},\mathrm{n}}^{{\mathrm{Y}}_{1}, {\mathrm{X}}_{1}}{\mathrm{l}}_{\mathrm{p}}\left({\mathrm{y}}_{\mathrm{m},\mathrm{n}}^{\mathrm{l}}\right)+\sum_{\mathrm{m},\mathrm{n},\mathrm{i},\mathrm{j}}{\mathrm{l}}_{\mathrm{p}}({\mathrm{w}}_{\mathrm{m},\mathrm{n},\mathrm{i},\mathrm{j}}^{\left(\mathrm{l}\right)}))$$

(74)

where ${l}_{p}$ is the calculated error in compliance with p-norm; ${y}_{m,n}^{l}$ is a vector in a channel of the lth layer, consisting of mth rows and nth columns; ${w}_{m,n,i,j}^{\left(l\right)}$ represents the filter through which neurons at m, n position of l layer is projected; ${\mathrm{Y}}_{1}\mathrm{ and }{\mathrm{X}}_{1}$ are the height and width of the layer arranged in a 3D box shape; and $\widehat{\mathrm{y}}$ and $\mathrm{y}$ denote the predicted and actual activity of neurons, respectively.

With limited research and understanding of brain processing, particularly of events associated with memory, learning, and attention, developing mature and complex deep predicting coding network architectures remains challenging. Therefore, visual image mapping requires further analysis. Nevertheless, many novel deep learning frameworks and applications employ the use of predictive coding across various fields for plethora machine learning applications. For instance, Dora et al. (2018) developed a generative model based on deep predictive coding and trained using unsupervised learning for processing real-world images and to effectively capture the statistical regularities of the data. Such ability makes the model suitable for various image classification and computer vision tasks. The application of a similar model in security is another prominent example.

The importance of machines to detect video anomalies is gaining popularity to enhance security and surveillance. However, video anomalies are highly ambiguous and complex, with high error margins and poor scores in existing reconstruction and prediction modules (Hasan et al. 2016; Liu et al. 2017; Ye et al. 2019). A recent application of deep learning by Ye et al. (2019) demonstrated an improved video anomaly detection. Using a predictive coding network with an error refinement module, the methodology was able to refine coarse predictions, reconstruct errors, and create a framework that assembles reconstruction and prediction modules. The modified predictive coding model uses a multilayer network that extracts prediction error features (Eqs. (75) and (76)). The new predictions are then generated to rectify prediction errors using the convolution of the ConvLSTM unit, enabling sequential dynamics modelling (Eq. (77)). Afterwards, the system performs refinement. To reach a refined estimation, score gaps between the frames (normal and abnormal) are reconstructed. Equation (79) represents the error refinement module based on Eq. (78). The objective functions were minimized and optimized. Metrics, including intensity (to measure pixel-wise difference), gradient (to prevent blurry predictions), and motion constraints, were utilized as a part of the adversarial training strategy.

$$\mathrm{PEP}: {\mathrm{E}}_{\mathrm{j}-1}={\mathrm{I}}_{\mathrm{j}-1}-{\widehat{\mathrm{I}}}_{(\mathrm{j}-1)}$$

(75)

where ${\mathrm{E}}_{\mathrm{j}-1}$ is the previous prediction error; ${\mathrm{I}}_{\mathrm{j}-1}$ represents the ground truth; and ${\widehat{\mathrm{I}}}_{(\mathrm{j}-1)}$ denotes the previous prediction.

$${\mathrm{R}}_{\mathrm{j}-1}=\mathrm{PEP}({\mathrm{E}}_{\mathrm{j}-1})$$

(76)

In Eq. (44), ${\mathrm{R}}_{\mathrm{j}-1}$ extracts deep features, and ${\mathrm{E}}_{\mathrm{j}-1}$ is the previous prediction error.

$$\widehat{{\mathrm{I}}_{\mathrm{j}}}=\mathrm{Conv}(\mathrm{ConvLSTM}\left({\mathrm{R}}_{\mathrm{j}-1}\right))$$

(77)

where $\widehat{{\mathrm{I}}_{\mathrm{j}}}$ is the updated prediction generated from the previous prediction error; and ConvLSTM is a special LSTM operation (spatial convolutions placed for connected transformations).

$$\Delta \mathrm{S}= \frac{{\sum }_{\mathrm{t}\in \mathrm{N}}{\mathrm{S}}_{\mathrm{t}}}{{\mathrm{T}}_{\mathrm{n}}}-\frac{{\sum }_{\mathrm{t}\in \mathrm{A}}{\mathrm{S}}_{\mathrm{t}}}{{\mathrm{T}}_{\mathrm{a}}}$$

(78)

where $\Delta \mathrm{S}$ is the regularity score gap for error refinement (between normal and abnormal frame); ${\mathrm{S}}_{\mathrm{t}}$ is the regularity score; t, time frame; N is the sequence number set for the normal frame; A is the sequence number set for the abnormal frame; and ${\mathrm{T}}_{\mathrm{n}}$ and ${\mathrm{T}}_{\mathrm{a}}$ denote the total number of normal and abnormal frames, respectively.

$$\widehat{{\mathrm{E}}_{\mathrm{t}}}=\mathrm{ERM}\left({\mathrm{E}}_{\mathrm{t}}\right)$$

(79)

where $\widehat{{\mathrm{E}}_{\mathrm{t}}}$ and ${\mathrm{E}}_{\mathrm{t}}$ are the updated prediction error and preceding prediction error of time step t, respectively.

Another novel method was proposed by Tandiya et al. (2018) based on deep parse coding to detect radio frequency (RF) anomalies that are present in wireless connections. The neural network was trained to recognize the anomaly when there is a potent deviation between the predicted and actual outcomes. The method performs real-time RF monitorization, which is both non-intrusive and automated. Tandiya et al. (2018) demonstrated that the use of deep predictive coding is faster and more efficient than other ML-based approaches. Sequenced images of the network’s normal operation were obtained using Prednet, a video frame detector, which teaches the network to make predictions and detect anomalies. Auto-tuning the hyperparameters could be one significant improvement for the predictive coding networks, using:

$${S}_{xx}^{\alpha }\left(n,f\right)=\frac{1}{N}\sum_{r=1}^{N}\frac{1}{{N}^{^{\prime}}}{X}_{{N}^{^{\prime}}}\left(n,f+\alpha /2\right){{X}^{*}}_{{N}^{^{\prime}}}(n,f-\alpha /2)$$

(80)

where α = cycle frequency as one axis.

The anomaly detection efficiency of this neural network was close to 100%. The seismocardiography-based detector showed to act relatively faster than the first detector, which is responsible for the detection anomaly in consecutive spectrogram images. The seismocardiography-based detector spots image anomalies almost instantaneously, and such a methodology of anomaly detection can be employed for networks with variable constraints and devices. However, the robustness of detection can be further improved by working with complex anomalies, evaluating longer run times, and employing machine learning techniques to process raw data in different forms. Showing promising error rates and efficient predictive capacity, each framework has its own merits and demerits. Given that predictive coding is an area that requires further understanding, the functions and frameworks applied by machine learning engineers to solve problems in various disciplines, with various biases, can be significantly improved and optimized further.

The main objective of sparse coding, a special case of deep predictive coding, is to determine a set of input vectors as a linear combination of basis vectors, which is then taught to efficiently represent data, as seen in Eq. (49) (for example, image data for classification). In a study by Zhang et al. (2017a, b, c), deep sparse coding (a deep modelling technique) produced effective results in extracting high distinct features from raw image pixels, for which the process is based on unsupervised learning. The deep sparse coding network is constructed upon basic input, a sparse-coding and pooling layer, and a normalization and map reduction layer. Such an algorithm uses heuristics to minimize non-convex functions. Although the system is dependent on a CNN architecture and could have improved speed, the overall framework is easier to code and functions better than any independent CNNs. However, deep sparse coding suffers from not being mathematically rigorous and converging towards a local minimum. Arora et al. (2015) demonstrated how sparse coding can also converge to a global minimum, providing a novel-based initialization method that returns a better starting point.

$${\text{C}}_{{{\text{ij}}}} = \arg \min \frac{1}{2}||{\text{x}}_{{{\text{i}},{\text{j}}}} - {\text{W}}_{{{\text{c}}_{{{\text{ij}}}} }} ||^{2} ,{\text{ s}}.{\text{t}}|\left| {{\text{c}}_{{{\text{ij}}}} } \right||_{{{\text{L}}_{0} }} { } \le {\text{ K}}$$

(81)

where X_ij is the receptive field at spatial location i, j; W represents the weight of the input; C is the number of colored channels (of the input layer), as well as the number of feature maps for the feature map layer (Zhang et al. 2017a, b, c); K controls the sparsity of ${\mathrm{c}}_{\mathrm{ij}}$; and ${\mathrm{L}}_{0}$ is a constraint under batch tree orthogonal matching pursuit.

$$C = \arg \min \frac{1}{2} \left\| {I - \mathop {\sum\nolimits_{m = 1}^{M} {w_{m} * C_{m} } }\limits_{{}}^{{}} } \right\|\begin{array}{*{20}c} 2 \\ F \\ \end{array} + \beta \mathop {\sum\nolimits_{m = 1}^{M} {\left| {C_{1} } \right|} }\limits_{m = 1}^{M}$$

(82)

where ${\mathrm{w}}_{\mathrm{m}}$ is the kernel; and ${\mathrm{C}}_{\mathrm{m}}$ is the sparse feature map.

Convolutional sparse coding network (CSN), based on Eq. (50), incorporates the framework of a convolutional system (Zhang et al. 2017c). Similar to a deep sparse coding network that primarily performs patch-level approximation, CSN conducts image-level reconstruction (approximation as well), but with more hindrance due to the convolution’s nature. Therefore, deep sparse coding was observed to propagate sharp information forward. The hierarchical sparse coding (HSC) framework is a similar working sparse coding network that completes the patch operation using concatenation methodology. For HSCs, map reduction layers are essential to delve deeper. Utilizing multi-level optimization and non-negative sparse coding, Sun et al. (2017) developed a multilayer sparse coding network. The latter system is a deep learning framework consisting of bottleneck modules with an expansion and reduction layer of sparse coding, consisting of wide and slim dictionaries that are able to generate high- and low-dimensional distinct features and clustered representations, respectively. A supervised learning technique was also employed to train the dictionaries, optimizing regulatory parameters. Although the network requires fewer layers and parameters, the deep learning architecture should be further studied to improve processing efficiency. The general descriptions of each deep learning modelling technique, as well as the main surveyed studies in terms of their main objectives, outcomes, and applications, have been summarized in Table 2.

Table 2 Overview of the studies conducted on deep learning modelling

5 Advantages and challenges of deep learning models

The several advantages underpinning deep learning models, including image processing and recognition, speech recognition, self-driving cars, and so on, have sparked such widespread attention. The main benefit of using deep learning models over machine learning (ML) technologies is their capacity to produce new features through a limited range of features in the trained dataset (Kotsiopoulos et al. 2021). These models can generate new tasks for solving current ones as well as they also cover a variety of human life aspects. A significant amount of time can be saved using deep learning models when dealing with massive datasets, as deep learning algorithms can generate features without the need for human intervention (Gupta et al. 2021).

Despite their numerous advantages, deep learning models have a number of noticeable challenges. First, they are unable to provide arguments supporting the fact that a particular conclusion is reached (Signorelli 2018). In addition, unlike typical machine learning, people are not able to follow an algorithm to figure out why the system decides that the image portrayed is a dog rather than a cat. To correct these types of errors in deep learning algorithms, the entire algorithm must be revised, which requires additional time. Also, high-performance computing units, high powerful GPUs and enormous quantities of storage are needed to train the models. Therefore, deep learning models require more time compared to traditional ML methods (Palanichamy 2019). The challenges of applying the deep learning models are summarized in Table 3 along with their advantages.

Table 3 Advantages and challenges of deep learning modelling techniques

In general, deep learning (DL) often produces better results as opposed to machine learning. For example, the largest data portion of an institute/organization is unstructured since it appears in so many different formats, including texts and images. Most machine learning (ML) algorithms struggle to make sense of unstructured data, therefore this type of data is underutilized. Herein lies the strength of deep learning. The main benefit of using DL over other ML algorithms is its capacity to produce novel features from limited sets of features already present in the training dataset. It follows that DL algorithms can devise new challenges to address existing problems. DL enables full-cycle learning by using neural networks' capability for featurization, from inputting raw data to producing an outcome. This approach allows for the optimization of all relevant parameters, which ultimately results in improved precision.

A key advantage of using the DL approach is that it can perform feature engineering on its own. In this method, the algorithm is not given any explicit instructions, but rather it automatically searches through the data for features that correlate and then combines them to facilitate faster learning. Because of its ability to handle massive data, DL scales extremely well. The algorithms of DL can be learned on a wide range of data formats while still producing insights relevant to the objectives of the training. For instance, DL algorithms can be utilized to identify correlations between social media activities, market research, and other factors in order to predict the future stock value of a particular firm.

There are a number of issues with DL models as well. In order to outperform alternative methods, deep learning needs access to a massive dataset. Therefore managing data is the key challenge that hinders DL in industrial implementations. Deep learning is currently limited in its applicability because of the extensive computer resources and training datasets it necessitates. It is still a mystery as to how exactly DL models arrive at their conclusions. Not like in traditional ML, where we can trace back the reasoning behind a system’s identification of a given image as representing a cat rather than a dog. To rectify errors in DL algorithms, the entire algorithm must be modified. However, no universally applicable theory is available that can help us to choose the appropriate DL tools as it needs knowledge of training methods, topology, and other features.

6 Comparative analysis of deep learning modelling techniques

Through the present review, it has been determined to what extent deep learning (DL) modelling techniques can be used in real-world applications. In addition, the methods employed, the outcomes, and the challenges of DL that have been modelled are identified. The comparative study compares available DL techniques based on their strengths and weaknesses, as well as performance metrics. The advantages and challenges outlined in the previous section make up the basis for the comparative study on strengths and weaknesses.

6.1 Comparative study based on weakness and strength

One of the common DL models, namely the vector space model (VSM) is found simple in structure and allows the computation of the similarity degree between documents and queries on a continuous scale. In contrast, the VSM assumes that words are statistically independent. Additionally, documents with a similar context and distinct term vocabulary will not be connected, resulting in a "false negative" match. Convolutional neural network (CNN), on the other hand, uses less time for classification and has good precision in image recognition challenges. However, comparatively larger data sets are required to train for CNN. Poor data labeling is another disadvantage of CNN, which can dramatically affect system performance and precision. Several classification issues, including image classification, have been successfully addressed using a predictive coding network (PCN). One of its drawbacks is that there is a lack of certainty regarding how the estimated error minimization functions.

It is observed that the recurrent neural network (RNN) is useful for time series forecasting. In RNN, weight remains constant across all levels, minimizing the number of parameters the network must learn. However, gradient and explosion vanishing issues limit the length of RNN sequences. Its computation process is comparatively slow because of its repeated/recurrent nature. However, for highly optimal execution, a long training period may be needed. In most cases, the efficiency and accuracy of the Hierarchical bidirectional recurrent neural network (HBRNN) are comparatively better than the other networks as it is constructed through the extensions of bidirectional recurrent neural network (BRNN) and RNN. Before predictions can be made with HBRNN, the full sequence must be accessible. On the basis of the scoring function, the recursive neural network (RvNN) is capable of detecting samples that are relatively similar to one another. Obtaining labeled data for RvNNs is an incredibly challenging and time-consuming task. Compared to a typical neural network layer, a neural tensor network (NTN) is a powerful tool for modelling relational data. Massive triplet samples are required for NTN to properly train, however, this has a little effect on sparse knowledge graphs on a global scale.

Deep belief network (DBN) enables highly efficient applications in the domains of handwriting, face, and speech recognition due to the model's continual learning of the characteristics of randomly input samples. However, DBNs do not account for the two-dimensional structure of input images, which could significantly affect their performance. Attention mechanism can deduce information from an input that is most pertinent to accomplishing a task, hence enhancing performance, especially in language processing. Ambiguous inputs can be handled by Deep Boltzmann machine (DBM) more robustly. DBM is capable of identifying latent features in data. One of the limitations of DBM is that maximum probabilistic learning in DBM is a challenge due to the hard inference issue caused by partition functions. The restricted Boltzmann machine (RBM) is comparatively faster than a traditional DBM because of the limitations in the number of connections among the nodes. But the process of learning an RBM is computationally intensive, and in the case of large datasets, the combined optimization of the parameters is not feasible due to the slower approximation interface of RBMs.

A well-generalized ability on smaller datasets makes capsule neural network (CapsNet) suitable for use in a wide range of applications. CapsNets are not able to perform consistently across various datasets, particularly large datasets such as ImageNet. Using hidden deterministic layers as opposed to hidden stochastic layers, the deep energy model (DEM) can perform interface and learn quickly. It is less popular due to computational difficulties and the difficulty of evaluating the likelihood (learning) in DEMs. A generative adversarial network (GAN) does not require estimating a probability distribution by introducing a lower bound like a variational autoencoder. But GAN has a mode collapse problem, and its data-generation process is intrinsically slow.

6.2 Comparative study based on performance criteria

This section compares the performance of several deep learning modelling techniques based on two key performance factors such as prediction accuracy and complexity level, which are crucial for suitable model selection. The study of the computational complexity of deep learning models is important because it can answer the fundamental question of why deep learning architecture performs substantially better than traditional machine learning algorithms. In addition, understanding the complexity is useful to analyze and compare different deep learning models and improve their performance. The complexity analysis of deep learning models highly depends on the model structure; on the other hand, the models are structurally different. Therefore, they cannot be generalized and directly compared to one another.

One of the recent studies (Hu et al. 2021) surveyed the latest research on model complexity in deep learning. In the study, four factors that influence the deep learning model complexity were surveyed: (i) model framework including activation functions such as tanh, ReLu, and others, (ii) model size, including the depths of the neural network layers and the number of trainable parameters, (iii) optimization process such as the number of iterations (epochs) to optimize the model, optimization algorithms, hyperparameters, and (iv) data complexity, which includes class imbalance and high dimensional data. The performance of a DL model also relies on other parameters such as hardware platforms (high-end GPU), compiler optimization, and implementation tools. Based on some of those factors and literature availability, we analyze the performance and computational complexity of different variants of deep learning models across different application fields (Seo et al. 2020; Zeroual et al. 2020; Cui et al. 2018; Vazhayil et al. 2018; Shakya et al. 2018), and classify them into three categories: Low, Medium, and High, as illustrated in Table 4. The lack of relevant comparative DL literature is identified as the key challenge behind this comparative survey.

Table 4 Comparison of different variants of deep learning architectures applied in different fields based on performance criteria and complexity

The time complexity of an algorithm mainly depends on the input data, and it can be described using the big-oh notation. Due to its complex nature of architecture, structural differences, and many other factors, the time complexity of the deep learning model is usually measured by how long it takes a model to solve a problem on specified hardware. An empirical analysis of how the configuration settings affect the running time of deep learning models was conducted by Lee and Chen (2020). The analysis demonstrated that model complexity increases the running time, but if the data quality is below average, it is not worthwhile to increase model complexity. In the sentiment analysis task, increasing the CNN model’s complexity may not improve the performance, whereas increasing the RNN model’s complexity invariably improves the model performance. Bi-LSTM is found to be superior to other CNN and RNN models for sentiment analysis (Seo et al. 2020). In malicious URL detection, CNN-LSTM gives comparatively high accuracy than ordinary CNN with a little more computational cost (Vazhayil et al. 2018). However, CNN shows a significant improvement over RNN-LSTM in computer vision tasks such as human activity recognition (Shakya et al. 2018). CNN is a better choice in intrusion detection systems if it is a binary classification problem (Cui et al. 2018). For multi-class classification, regular CNN performs poor than others while RNN is a good choice because of the sequential data. It is much more computationally expensive than RNN in its architecture. Compared to RNN, Auto Encoder (AE) shows superior performance in forecasting time-series data. But RNN is relatively faster and needs less computational cost than LSTM, Bi-LSTM, and AE (Zeroual et al. 2020).

7 Future of deep learning

As we step foot into a new era of surplus big data and information, the future of deep learning is not only prominent but vital for the advancement, resilience, and problem-solving endeavors of the globe. Deep learning has become a necessary tool across every discipline from science, engineering, humanity, and health to climate studies and many more. From developing cybersecurity and surveillance to performing quantum computing, deep learning will be an evident constant of the future. With the great success of deep networks in the field of computer vision and the development of artificial intelligence, being able to extract meaningful and correct features from data to generate necessary outcomes, without discrimination and being more tolerant of nuisance variations in data (Deng 2014; Guo et al. 2016), deep learning is the basis for future innovations. As of yet, further knowledge and understanding are required to improve and construct deep learning networks that deal with complex high dimensionality data and variations to characterize inputs and outputs efficiently (Kato et al. 2016).

The growing interest in investments, particularly of giant tech companies (Google, Facebook, Apple), represents and signals the value and potency of deep learning in the present and future. Although deep learning demands high computational power and constant training to generate reliable results, more work is yet to be done to ensure that deep learning networks are efficient and cost-effective in extracting and identifying distinct features from real-world data, mimicking the ability of biological intelligence. Therefore, when constructing a deep learning methodology, it is important to ensure that the model can deal with uncertainty, is scalable, and has transferable qualities to be implemented and applied to multiple problem systems (Zhang et al. 2020). Alongside the development of deep learning techniques, the availability of user-friendly hardware and software systems are significant future prospects for deep learning.

Larger and more extensive datasets are necessary for enhancing the performance of DL models in a complex and dynamic construction environment including many human resources, several types of equipment, and a variety of human and equipment activities (Fink et al. 2020). As humanity surfs the wave of artificial intelligence and deep learning, ethical frameworks must be developed to ensure the sound employment and enhancement of deep learning techniques in order to manage proper conduction and utilization of big data that are fed into deep learning architectures, subsequently generating beneficial and sustainable solutions. Due to the small sample size of training and limited unsafe activities considered, several workers’ actions can not be recognized (Ding et al. 2018). With a larger dataset, the model can therefore improve and give more precise results. Nevertheless, there is presently no publicly available complete and standardized dataset, also for particular tasks like activity recognition, pose detection and object detection, as well as for different views, a wide range of construction sites, occlusion circumstances, and lighting.

Combining deep learning with expert knowledge can be a fruitful area of research since models may be dynamically augmented with acquired new data, resulting in effective digital twins which can help in maintenance decision making. Despite the fact that physics-induced deep learning is now pursuing multiple directions, there is no agreement or no consolidation on various directions as well as how they can be translated to industrial applications. There is a need for additional studies to refine and consolidate these techniques, which may help increase the generalization ability of the models developed. Another issue that must be addressed in future studies is the effective selection and composition of sets of training data. This is especially important in environments that are constantly changing and have extremely variable operating conditions, where the training dataset is not representative of the whole range of predicted operating conditions. Continuous decisions must be made as to whether new data needs to be included in training datasets and the algorithms updated, or whether the information is repetitive and included already in the datasets used for training the algorithms.

8 Conclusion

Deep learning (DL) is a thriving multidisciplinary field that is still in its nascent phase. With the growing availability of data, DL architectures can be successfully applied to problems across various sectors in the modern world. This paper provides a comprehensive systematic review of the state-of-the-art DL modelling techniques. Some models can be trained by two or more methods, which means their efficiency relies on the domain in which they are used. The use of hierarchical layers for proper data classification, as well as supervision in learning to determine the importance of the database of interest, are both important factors to develop robust DL models. While nearly all of the models display robustness to some extent, existing techniques are still flawed, which subjects them to criticisms. With the availability of big data across various domains, the quality of data can become an issue when training DL models. Training DL models can also be very time-consuming, expensive, and requires hundreds of correct examples for better accuracy, which can limit their use for everyday purposes or in sensitive security systems. The resulting models may also be domain-specific and, therefore, may have restricted applications. In addition, DL is susceptible to deception and misclassification, which can threaten the social and financial securities of individuals and/or corporations. Getting stuck on local minima also makes most models unsuitable for online modes.

CNNs, RNNs, GANs, and autoencoders are the more frequently used DL architectures across various sectors. However, the potential application of other architectures in current areas that use DL is widely unexplored. This paper found that advanced DL models, which are essentially hybrid conventional DL architectures, have the potential to overcome the challenges experienced by conventional models. Moreover, generative models exhibit greater capabilities as they are less reliant on examples. Future networks should strive to generate a set of possible outcomes, instead of providing one final prediction for the input, which may help tackle the issue of distorted or unclear inputs. Developing new strategies to optimize parameters, particularly hyperparameters, is another possibility that requires further investigation. Capsule architectures may dominate future DL models as they offer an enhanced way of routing information between layers. If the current challenges can be addressed, DL models can potentially contribute to further innovations in the field of AI and for solving far more complex problems.