Topological triplon modes and bound states in a Shastry–Sutherland magnet

Abstract

The twin discoveries of the quantum Hall effect¹, in the 1980s, and of topological band insulators², in the 2000s, were landmarks in physics that enriched our view of the electronic properties of solids. In a nutshell, these discoveries have taught us that quantum mechanical wavefunctions in crystalline solids may carry nontrivial topological invariants which have ramifications for the observable physics. One of the side effects of the recent topological insulator revolution has been that such physics is much more widespread than was appreciated ten years ago. For example, while topological insulators were originally studied in the context of electron wavefunctions, recent work has initiated a hunt for topological insulators in bosonic systems: in photonic crystals^3,4,5,6, in the vibrational modes of crystals⁷, and in the excitations of ordered magnets⁸. Using inelastic neutron scattering along with theoretical calculations, we demonstrate that, in a weak magnetic field, the dimerized quantum magnet SrCu₂(BO₃)₂ is a bosonic topological insulator with topologically protected chiral edge modes of triplon excitations.

Main

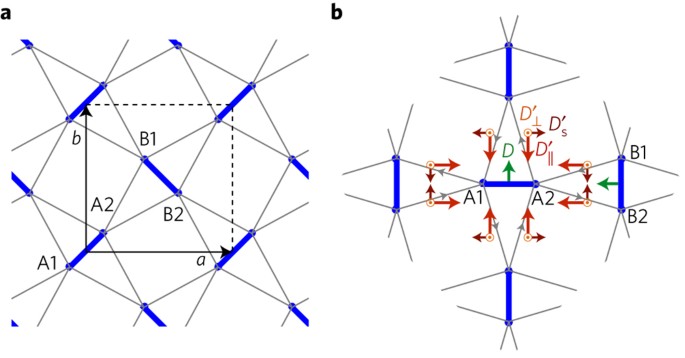
The quantum magnet SrCu₂(BO₃)₂ is famous in the magnetism community⁹ especially for its rich in-field phase diagram reflected in a series of magnetization plateaux^10,11. The material is composed of layers of strongly interacting S = 1/2 copper moments arranged on the lattice illustrated in Fig. 1. Nearest-neighbour moments bind together in pairs (dimers), forming quantum mechanical singlets. Neighbouring dimers have an orthogonal arrangement (Fig. 1). Most magnetic materials undergo a transition into long-range magnetic order, so the fact that the ground state of this material is both interacting and with only short-range correlations is remarkable: a consequence of the frustrating effect of the Shastry–Sutherland lattice geometry^12,13. The lattice geometry of SrCu₂(BO₃)₂ is also responsible for ensuring that the excited states of the magnet—called triplons—are almost flat across the Brillouin zone^14,15,16. The predominant contribution to the weak dispersion of these modes is due to subleading magnetic exchange couplings which are antisymmetric Dzyaloshinskii–Moriya (DM) interactions^17,18.

Figure 1: Symmetries and exchange on the magnetic lattice of SrCu₂(BO₃)₂.

a, A section from the lattice of copper ions in SrCu₂ (BO₃)₂. The lattice axes a and b are marked together with the copper sites 1 and 2 on each sublattice A and B. The copper–copper singlets are indicated by the thick blue lines which are coupled by exchange coupling J. Neighbouring singlets joined by light grey bonds are coupled by J′ exchange. The crystallographic unit cell is the dashed square. b, Conventions and symmetries of the DM exchange D_ij ⋅ (S_i × S_j). Only one component of the intra-dimer DM exchange D (green) is allowed by symmetry, whereas all three components are allowed for the inter-dimer coupling: staggered and parallel in-plane components, D_s′ (dark red) and D_∥′ (red), and a uniform component D_⊥′ (orange) perpendicular to the plane. The bond orientations are from site 1 to 2 within each dimer and indicated by grey arrows for the inter-dimer bonds.

These DM interactions are responsible for complex hopping amplitudes of the triplons which may then pick up Berry phases around closed paths. Their role is therefore similar to that of spin–orbit coupling in electronic topological insulators. Based on a theoretical model of non-interacting triplons, Romhanyi et al. ¹⁹ predicted that in a small magnetic field the triplon bands of SrCu₂(BO₃)₂ acquire a nontrivial topological invariant, called a Chern number, which implies the existence of chiral magnetic edge states.

In this Letter, we present new inelastic neutron scattering (INS) results exploring the low-energy magnetic excitations of SrCu₂(BO₃)₂ in small magnetic fields of up to 2.8 T perpendicular to the dimer planes. This provides unprecedented insight into the nature of the magnetic couplings in this material. In addition to the triplon bands, we find a new field-independent and comparatively dispersive feature that hybridizes with them. We identify this mode as a singlet bound state of two triplons²⁰. Its presence is a manifestation of the strong interactions between triplons and a precursor of the complex crystals of bound states¹¹ that give rise to the magnetization plateaux at higher fields. While one expects the topological character of the triplon excitations to be protected against smooth deformations of the band structure, the hybridization with the bound state does not represent such a continuous deformation. A model of free triplons is therefore inadequate to address the topology of the magnetic excitations in SrCu₂(BO₃)₂. Using a comprehensive theoretical model, we show that the hybridization with the bound state does not destroy the topology but makes it even richer, increasing the number of topological bands and leading to a sequence of topological transitions. We make predictions for the thermal Hall effect and the presence of edge states.

Crystals were grown with 99%-enriched boron-11 by the optical floating zone technique²¹ at 0.25 mm h^−1 under 3 bar oxygen pressure. The sample mount consisted in three single crystals of total mass 5.9 g, which were co-aligned on the ALF instrument at ISIS on an aluminium mount with the a and b axes in the horizontal scattering plane. Our INS measurements were performed using the direct geometry time-of-flight spectrometer, LET, at the ISIS facility²². The sample was mounted inside a 9 T superconducting magnet and the sample was cooled down to 2 K. The measurements were performed with multiple incident energies, of which we focus here on the 5 meV data. We collected multi-angle Horace²³ scans with 1° step sizes at 0 T and 1.4 T and 2° step sizes at 0.7 T and 2.8 T with a 68° total coverage and a 38 min counting time per angular step. The experimental resolution (full-width at half-maximum) at the elastic line at E_i = 5 meV was measured to be 120 μeV. The calculated energy resolution at 3 meV energy transfer is 70 μeV.

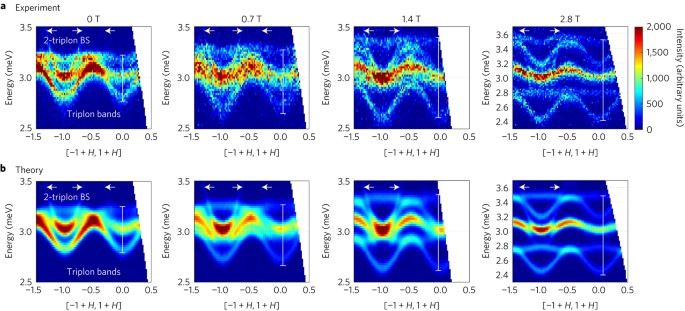
Figure 2a shows INS cuts along the [−1 + H, 1 + H] direction for magnetic fields 0 T, 0.7 T, 1.4 T and 2.8 T. Other momentum cuts can be found in the Supplementary Information. Since the unit cell contains two dimers, there exist six triplon bands, which are most clearly resolved at B = 2.8 T. As expected, the triplon bands have a strong field dependence. At zero field, the gap to the triplons is roughly 3 meV, which is the scale of the nearest-neighbour isotropic exchange J. Instead of the predicted¹⁹ spin-1 analogue of a Dirac point with an almost flat band crossing through this point we find that the modes are non-degenerate at zero field, indicative of a significant anisotropy in the system.

Figure 2: Evolution of the low-energy magnetic excitations of SrCu₂(BO₃)₂ in a field along the [001] direction with cut taken in the [−1 + H, 1 + H] direction.

a, Data taken at zero field, 0.7 T, 1.4 T, and 2.8 T. These cuts were integrated in the L direction between ±0.2 and in other directions between ±0.1. In addition to the triplon bands, the data show a relatively dispersive, field-independent mode. We identify this mode as a singlet bound state of two triplons, visible in the magnetic structure factor only through the strong hybridization with the triplon excitations. b, Calculated spectra using a model of interacting triplons that is derived from a bond-operator expansion of the initial spin Hamiltonian.

In addition to the single-triplon excitations, Fig. 2 shows a more dispersive mode that intersects them with a minimum at the Γ point at around 3 meV, which is roughly in the middle of the triplon bands. This feature was not apparent in earlier INS data (taken in zero field)¹⁵. The intensity of this mode just above the triplon modes is around three percent of the maximum intensity of the triplon modes and can be observed using LET because of the high sensitivity of the spectrometer. A constant energy cut at 3.3 meV (Supplementary Information), slightly above the triplon bands, shows rings of intensity coming from the additional mode, which meet the Brillouin zone edge at about 3.8 meV. An applied field has no apparent effect on the dispersion relation of the mode (see Fig. 2 and Supplementary Information).

Among other reasons (Supplementary Information), the strong hybridization of the mode with the triplon excitations and the disappearance of the mode at 15 K when the triplon intensity is absent clearly speak against a phonon interpretation of the new dispersive feature and instead point towards a magnetic origin. Indeed we will demonstrate that the mode is a singlet bound state of two triplons. This explains why the mode is independent of the field and visible in the magnetic structure factor only through the strong hybridization with the triplons.

To understand the experimental dispersion, we consider all symmetry-allowed couplings between first- and second-neighbour spins. There are four allowed intra-dimer exchange couplings—the isotropic exchange J, a Dzyaloshinskii–Moriya (DM) coupling D with D vectors shown in Fig. 1b, an Ising coupling J_zz, and a symmetric exchange J_xy. The corresponding single-dimer Hamiltonian is given by

where we have included the Zeeman term for a field perpendicular to the Shastry–Sutherland planes. Note that, by symmetry, the J_xy coupling is of opposite sign on the two sublattices of A and B dimers (see Fig. 1). Owing to the weak spin–orbit, we a priori expect the hierarchy of energy scales J > D > J_zz, J_xy. We use the bond-operator formalism^24,25 to represent the two spins of each dimer in terms of singlet and triplet operators, S₁^α − S₂^α = s^†t_α + t_α^†s and S₁^α + S₂^α = −iε_αβγt_β^†t_γ. The operators s^† and t_α^† (α = x, y, z) create dimer singlet and triplet states out of the vacuum, respectively, and are subject to the usual hard-core constraint s^†s + ∑ _αt_α^†t_α = 1. The coupling between dimers gives dynamics to the triplon excitations. Again, the largest such coupling between next-nearest-neighbour spins is the isotropic component J′ of the Heisenberg exchange, followed by the DM coupling D′. There are no symmetry constraints on the components of D′ on a bond but, once those are fixed, they are determined over the entire lattice (see Fig. 1b).

We condense the singlets into the ground state and perform a unitary rotation to eliminate linear terms in the triplet operators arising from the intra-dimer DM interaction D. The triplon dispersions are computed by diagonalizing the quadratic triplon Hamiltonian, given in the Methods. In the Hamiltonian we keep DM terms only to linear order. It turns out that only two of the three components of the inter-dimer DM exchange, D_⊥′ and D_∥′, contribute. It is well known¹⁹ that a dispersion in the single triplons coming from J′ (in the absence of DM interactions) arises only to sixth order in J′/J. We neglect this lowest-order contribution to the triplon hopping. The anomalous terms that arise in the bond-operator expansion give only a negligible correction to the triplon dispersion (Supplementary Information). In summary, we obtain six triplon bands since there exist two dimers in the unit cell. These triplon excitations depend on five parameters (J, J_zz, J_xy, D_⊥′, and D_{∥, eff}′), where the parallel component of D′ is shifted due to the aforementioned rotation, D_{∥, eff}′ = D_∥′ + (1/2)DJ′/J. Following ref. 19, we also include a small further-neighbour triplon hopping term J_FN between dimers on the same sublattices.

The bond-operator representation leads to cubic and quartic interaction terms between the triplons (see Methods) which are responsible for a tower of bound states^9,20. To study the bound states in the singlet sector, as motivated by the experiment, we follow and extend the results of ref. 20. A singlet bound state of two triplons has a wavefunction . We approximate this wavefunction by carrying out degenerate perturbation theory in J′ to third order within the two-triplon sector (see Methods). This generates nearest- and next-nearest-neighbour potentials and effective hopping terms, and requires us to consider eight localized two-triplon states. There is no linear contribution of the DM interactions to the bound-state sector. As for the single triplons we neglect higher-order DM terms. It turns out that, to third order in J′, two pairs of four such states decouple, leading to degeneracies that are artefacts of the low-order perturbation theory. Therefore, we include those terms to fourth order in J′ that are necessary to couple these sectors. Diagonalization of this Hamiltonian leads to four bound states and four anti-bound states. The lowest energy bound state is at the Brillouin zone centre, as observed experimentally (see Fig. 2). Since J′/J ≈ 0.6 (ref. 26) is not small the perturbative expansion might not be very well controlled. On the other hand, high-order perturbation theory up to 14th order shows that the bound state is a robust feature²⁶. In the spirit of effective field theory, we will use the perturbation theory to determine the general structure of the Hamiltonian but allow the resulting parameters to be determined by experiment.

The spin Hamiltonian described above—which is the minimal model necessary to describe the single-triplon and S = 0 two-triplon sectors—provides a natural explanation for the existence of a significant hybridization between these sectors. The DM interaction gives rise to a cubic triplon term that linearly couples the bound state and single-triplon sectors (see Methods). Once the bound state mixes some single-triplon character we also understand how the bound state acquires some neutron-scattering intensity given that the singlet sector on its own and the ground state are not coupled by neutrons. Note that the DM exchange gives a vertex for the decay of an S = 0 state into an S = 1 state. The coupling is not rotationally symmetric, and hence does not conserve angular momentum on its own. The angular momentum is taken up by the lattice, highlighting the importance of spin–orbit coupling to the existence of antisymmetric exchange. The above method may be used to study S = 1 and S = 2 two-triplon bound states²⁰. Within the model these naturally lie at higher energies than the lowest energy singlet sector. And, indeed, it appears that the lowest energy S = 1 bound states in SrCu₂(BO₃)₂ lie just below the two-triplon continuum^14,16.

We have seen that the model of interacting triplons, which is derived from a bond-operator expansion of the original spin Hamiltonian, straightforwardly allows for the existence of a singlet bound state and its coupling to the triplon excitations. We now consider the validity of this model as an explanation for our INS results on SrCu₂(BO₃)₂. We take constant k cuts through the data and fit the peaks to Gaussians with variable mean and variance, taking the minimal number of Gaussians necessary to obtain a good fit to each cut. In this way we obtain a set of points tracking the dispersion curves of the triplon and bound-state modes. To these points, we fit the theoretical model of interacting triplons, using a least squares minimization algorithm.

The parameters that enter the free-triplon Hamiltonian are obtained as J = 3.08 ± 0.002 meV, J_zz = 0.024 ± 0.002 meV, J_xy = 0.01 ± 0.003 meV,D_⊥′ = −0.0973 ± 0.001 meV, D_{∥, eff}′ = D_∥′ + (1/2)DJ′/J = 0.085 ± 0.005 meV, J_FN = −0.036 ± 0.005 meV and g_z = 2.28. The value for J should be viewed as an effective, renormalized one, since the perturbative corrections from the triplon interactions ∼J′ reduce the triplon gap considerably (see Methods). The potential energies and hopping amplitudes of the two-triplon states that contribute to the singlet bound state, as well as the parameters that describe their hybridization with the triplon excitations, are given in the Methods. The comparison of the theoretical and measured excitation spectra is shown in Fig. 2b for four different field strengths and for a cut in the [−1 + H, 1 + H] direction. Details of the calculation of the dynamical structure factor are given in the Methods. Spectra along various other cuts and a quantitative comparison of the observed and calculated intensities can be found in the Supplementary Information.

Our model provides an excellent description of the INS data and can now be used to investigate the topological nature of the magnetic excitations. Already on the level of the triplon bands we find significant differences compared to the model used in the original theoretical proposal¹⁹. First, the central triplon bands of SrCu₂(BO₃)₂ are much more dispersive and, in the regime of small fields, their bandwidth overlaps significantly with those of the upper and lower triplon bands. Second, in zero field there exist no Dirac points in the spectrum and instead we find small gaps, which are due to the presence of small anisotropic intra-dimer exchanges J_zz and J_xy. In addition, we have found clear evidence of a two-triplon singlet bound state that hybridizes with the triplon bands.

To analyse whether, in the presence of these new features, the magnetic excitations exhibit a nontrivial topological character, we calculate the first Chern number C_n for each band. This integer topological invariant is defined as an integral of the Berry curvature of the band over the two-dimensional Brillouin zone (see Methods). For the free-triplon model without anisotropic exchanges it is possible to give an intuitive, geometrical interpretation of the Chern numbers¹⁹. Because of a symmetry transformation between the dimers on the A and B sublattices, this model can be reduced to an effective three-band model H = ∑ _ij ∫ _kt_i^†(k)M_ij(k)t_j(k), with a coupling matrix of the form M(k) = J 1 + d(k) ⋅ L, where L is a vector of the 3 × 3 matrices L_x, L_y, L_z that represent spin-1 angular momentum operators. The vector field d(k) defines a mapping of the two-dimensional Brillouin zone (equivalent to a torus) to a closed surface embedded in three-dimensional space. The Chern number is equal to the number of times this surface wraps around the origin. For the full model with six triplon bands and bound-state modes, one requires a higher-dimensional generalization of the above mapping. Although the Chern numbers can still be interpreted as winding numbers, the geometrical picture is much less intuitive.

The Chern number is connected to observable quantities. In integer quantum Hall systems, for example, it is related to the quantized Hall conductance²⁷. A bosonic analogue of this result for the case when the band is thermally populated is the thermal Hall effect which, rather than depending on the Chern number and yielding a quantized response, instead depends on the magnitude of the Berry curvature in thermally occupied parts of the band^28,29. A topological transition is visible as a kink in the Hall effect resulting from a spike in the Berry curvature at the touching point between topologically nontrivial bands with equal and opposite Chern numbers.

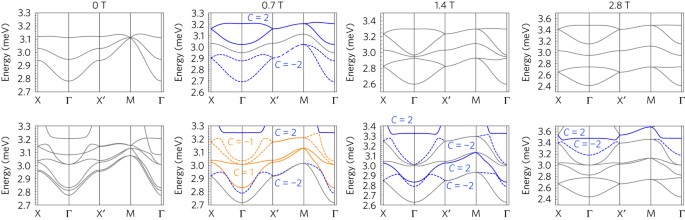
For the idealized triplon model of Romhanyi et al. ¹⁹ there exist only two topologically nontrivial triplon bands with Chern numbers C = +2 and C = −2 and a single finite field topological transition at the upper critical field B_c = 1.4 T. At B_c these bands touch at the Γ point and, as expected, the thermal Hall effects shows a kink. For our refined model the situation turns out to be much richer. Even without the bound state, the anisotropic exchanges J_zz and J_xy lead to the presence of two topological transitions. The hybridization with the bound state gives rise to a large number of bands with non-zero Chern numbers. Not surprisingly, we therefore find a sequence of topological transitions involving different pairs of bands. This is also reflected by the extremely rich structure of the thermal Hall effects (Supplementary Information). Fig. 3 shows the Chern numbers and dispersions of the low-energy bands at four different fields for the idealized model of Romhanyi et al. ¹⁹ and our refined model that includes the hybridization with the bound state and provides an excellent description of the measured magnetic excitations of SrCu₂(BO₃)₂.

Figure 3: Chern numbers of triplon bands and lowest singlet bound state.

The upper figures show the prediction of the model of ref. 19 but using the best-fit parameters determined from our experiment. The dispersions are shown along a high-symmetry path. Between 0 T and 1.4 T two triplon bands have nontrivial Chern numbers C = ±2. A touching point at 1.4 T leads to all bands being topologically trivial at higher fields. The lower figures show the predictions at four fields of the full model including the bound state. In contrast to the earlier work, we expect that Chern numbers of C = ±1 and C = ±3 arise in the band structure for certain fields with C = ±1 and C = ±2 present at 0.7 T. In addition, nontrivial bands persist to much higher fields B > 1.4 T. Note that the Chern numbers of the bands shown in the figure sum to zero.

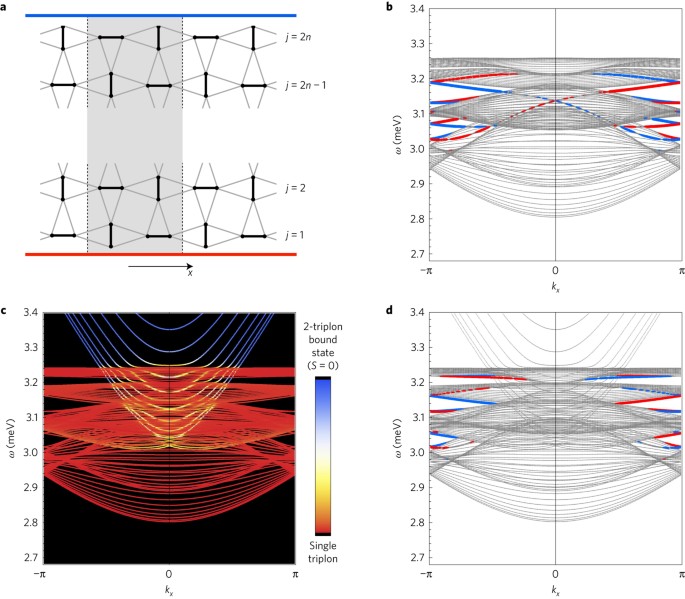
Another signature of the topological nature of bulk bands is the occurrence of protected edge modes. In the following, we consider a strip with 2n rows of dimers along the y direction (see Fig. 4a) and calculate the excitation spectrum of our model Hamiltonian as a function of the momentum k_x along the infinite direction. As expected from the Chern number calculation, we indeed find edge modes that are localized in the two upper or lower rows of the strip, shown in blue and red, respectively. However, over a large momentum range, the edge states are obscured by the quasi continua of bulk bands with quantized momenta k_y(j) = πj/n. To analyse this in more detail, we first switch off the bound state (Fig. 4b). In this case one expects¹⁹ edge states that live between the continua of the upper and lower triplon bands with Chern numbers C = +2 and C = −2, respectively. Unfortunately, the gap between the topological Chern bands is almost completely filled by the topologically trivial central triplon bands. As a result, edge states are visible only at momenta close to the zone boundary. As a next step, we include the bound state, which hybridizes with the triplon bands and increases the number of topologically nontrivial bands (see Fig. 3). Edge states remain visible near the zone boundary, and show complex evolution as a function of field (Supplementary Information).

Figure 4: Edge states.

a, Strip geometry used for our edge-state calculation. b, Excitation spectrum of a strip with 20 rows of dimers for the single-triplon model (without bound state) in a field B = 0.35 T perpendicular to the dimer plane. Edge states are identified as modes that are localized near the lower and upper edges of the strip, shown in red and blue, respectively. c,d, Spectrum of the full model including the S = 0 two-triplon bound state. c, Hybridization between the triplon modes and the bound state, indicated by the colour gradient. d, Identification of edge states.

Using INS, we have explored the evolution of the magnetic excitations in the gapped dimer system SrCu₂(BO₃)₂ as a function of a small magnetic field. In addition to the weakly dispersive triplon excitations, we identified an S = 0 two-triplon bound state. This singlet mode is comparatively dispersive and visible in the magnetic structure factor only because it hybridizes with the triplon bands. So far, hints of low-energy bound states have been found only in Raman^30,31 and electron spin resonance (ESR)³² experiments. The presence of low-lying bound states may be responsible for the remarkable sensitivity of triplon coherence to thermal fluctuations³³. Using the unprecedented insight we have gained into the nature of the magnetic excitations in this material, we have determined a minimal spin model that provides an excellent description of the neutron-scattering intensity, including that of the singlet bound state. For this comprehensive model we have calculated the Chern numbers of the bands and the edge-state spectrum. Although the magnetic excitations are much richer than originally proposed, our work shows that SrCu₂(BO₃)₂ is one of the first clear-cut examples of a bosonic topological insulator. For the future, it would be very interesting to learn how to probe the magnetic edge states in this material, as well as how to manipulate them.

Methods

Lattice convention and exchange couplings.

Below 395 K, SrCu₂(BO₃)₂ adopts the tetragonal structure (number 121). The magnetic ions are the copper Cu²⁺ ions which occupy the 8i Wyckoff positions with x = 0.114 and z = 0.288. The lattice constants of the tetragonal cell are a = 8.99 Å and c = 6.648 Å. They form a layered structure stacked along the c direction. One such layer is shown in Fig. 1a. Although there exists a small buckling, the copper bonds A and B are almost coplanar. The short bonds (marked in blue) between neighbouring copper ions are associated with the strongest exchange coupling J, which is antiferromagnetic. In the tetragonal primitive cell, the basis in units of the edge length in each direction is A1: (x, x, z), A2: (−x, −x, z), B1: (x, −x, −z), and B2: (−x, x, −z), relative both to (0,0,0) and to the body centre (1/2,1/2,1/2). The vertical separation between copper bonds A and B is (4z − 1)c/2 and the layers are separated by a layer of strontium.

The point group D_2d associated with consists of a C₂ rotation around the c axis and C₂ rotations around the a axes. Also, there are reflection planes: [110] and and an S₄ with c as the rotation axis. These symmetries constrain the types of exchange that can arise between the copper ions. For example, within nearest-neighbour copper bonds labelled by A, the possible types of exchange are S₁^xS₂^x + S₁^yS₂^y, S₁^zS₂^z, S₁^xS₂^y + S₁^yS₂^x and S₁^xS₂^z + S₁^yS₂^z − S₁^zS₂^x − S₁^zS₂^y. The latter coupling is an intra-dimer Dzyaloshinskii–Moriya (DM) coupling D_ij ⋅ (S_i × S_j). Symmetry also constrains the exchange on the B bonds. Referring to Fig. 1b for the lattice directions, the DM vector for the A bonds points in the vertical direction (0, D, 0) and for the B bonds in the negative horizontal direction (−D, 0,0), where the orientation i → j is always from site 1 to site 2.

For Cu²⁺ (d⁹) with spin one-half, the a priori superexchange should be mainly isotropic, with a smaller DM coupling to leading order in the (weak) spin–orbit coupling, with the symmetric anisotropic exchange being weaker still. The nearest-neighbour magneto-static dipolar coupling is 0.0088 meV.

Symmetry does not constrain the exchange at all on any given bond connecting neighbouring A and B sites. However, once the exchange is fixed on such a bond, all other such bonds are determined (see Fig. 1b). So there are nine distinct exchange couplings between neighbouring dimer bonds. Of these, isotropic exchange J′ is expected to be largest, followed by the antisymmetric exchange, which contributes three parameters to the exchange Hamiltonian.

Interactions in bond-operator language.

For each dimer we introduce bond operators that create singlet and triplet states from the vacuum. Expressing the spin-(1/2) operators by the bond operators, using the mapping given in the main text, the intra-dimer Heisenberg exchange can be written as

after imposing the constraint. The intra-dimer DM interactions mix singlet and triplet states,

We may remove these terms, thus diagonalizing the intra-dimer Hamiltonian, by performing a unitary transformation on the singlet and triplet operators. Instead of using the full transformation, we note that D/J ∼ 0.1, so we perform the rotation to order D/J. In particular, on the A bonds, we go to and operators which are

while on the B bonds we have

Now we consider exchange coupling neighbouring dimers. The most important of the symmetry-allowed exchange couplings is isotropic with coupling J′. We write this in terms of triplet operators on each J′ bond and sum over the two bonds connecting each pair of dimers. This gives H₃ + H₄, where

Here, s(j) is the site label, 1 or 2 of site j and there is no double-counting on bonds in the sums. The three-body terms, H₃ may create or annihilate triplets on two of the four dimer bonds neighbouring a given dimer. The single-particle triplon hopping term originating from J′ on its own vanishes owing to the geometrical frustration of the lattice.

The inter-dimer DM interaction, when written in terms of singlet and triplet operators, generates hopping terms between A and B dimers. Of the three DM couplings, the contribution coming from D_s′ cancels, leaving hopping depending only on D_∥′ and D_⊥′. The hopping Hamiltonian originating from these terms takes the form

where

and M^AB = M^BA(D_⊥′ → − D_⊥′).

We now discuss the effects of the transformation of the ground state and triplon operators brought about by the presence of the intra-dimer DM interaction D. Whereas the J′ coupling does not lead to hopping on its own, the rotation introduces hopping terms to order DJ′/J. One may show that these terms amount to a shift of the D_∥′ hopping terms coming from the inter-dimer DM exchange. More precisely, D_∥′ → D_{∥, eff}′ = D_∥′ + DJ′/2J.

We have understood that, besides isotropic exchange and DM couplings, there are two further anisotropic exchange couplings within each dimer allowed by symmetry. These terms lead to triplon terms of the form t_z^†t_z and t_x^†t_y + t_y^†t_x for S₁^zS₂^z and S₁^xS₂^y + S₁^yS₂^x, respectively. For the inter-dimer exchange, we have considered four couplings out of a possible nine, one of which—the isotropic exchange coupling—does not contribute to the hopping to lowest order in J′. The remaining anisotropic terms are symmetric, and hence do not lead to leading-order hopping terms.

The authors of ref. 19 observed that the single-triplon Hamiltonian with J, the DM couplings and hopping between second-neighbour dimers has equivalent sublattices A and B. This means that the Brillouin zone can be unfolded so that there are three bands in the zone. The explicit transformation that makes this translational invariance manifest is given in the Supplementary Methods of ref. 19. We note that this translational symmetry is broken by the presence of the pseudo-dipolar coupling J_xy.

Perturbation theory in J′.

Here we outline the perturbation theory in J′ within a fixed triplet number sector and in the absence of DM interactions. To zeroth order in perturbation theory, the state of the system is determined by J alone—it is a direct product of singlets in the ground state and degenerate triplet states on each site. We organize the perturbation theory as an effective Hamiltonian of the form H_eff = H⁽⁰⁾ + (J′/J)H⁽¹⁾ + (J′/J)²H⁽²⁾ + … computed from the full Hamiltonian H = H⁽⁰⁾ + V . To do this we introduce a projector onto the degenerate zeroth-order triplet sector with N triplets and a resolvent operator that connects the system to states |E〉 outside this sector. Here ε_S is the energy computed from H⁽⁰⁾ for state S. Then .

By carrying out perturbation theory in powers of J′/J we see that triplet hopping first appears to order (J′/J)⁶. So, the triplon modes acquire only a weak dispersion in J′. The ground state is even more resistant to the presence of J′: remarkably, in the J, J′ model, the direct product state of singlets on the dimer bonds is the exact ground state for J′ < J_c′ ≈ 0.68J. This is the celebrated result of Shastry and Sutherland^12,13. Although hopping of triplons is suppressed up to the order (J′/J)⁶, the energy of a single triplon is shifted by the presence of the inter-dimer exchange even at the second order. We find,

We further develop this perturbation theory below to address the presence and nature of the bound states.

Free-triplon Hamiltonian.

The Hamiltonian including intra-dimer isotropic and anisotropic exchange contributions as well as inter-dimer DM is given by H_ST = ∫ _kT_k^†Λ_kT_k, where T_k^† = (t_{k, A}^†, t_{k, B}^†) with t_{k, α}^† = (t_{k, α, x}^†, t_{k, α, y}^†, t_{k, α, z}^†), and

We use the following Fourier transform convention throughout

where i is the Bravais lattice site label with lattice vector R_i and s is the A or B sublattice with two-dimensional lattice vectors r_A = (0,0) and r_B = a(1/2,1/2).

The coupling matrix on sublattice A is given by

while the corresponding matrix B_k on sublattice B is obtained from A_k by inverting the sign of J_xy. Finally, the coupling between the sublattices takes the form

where for brevity, we have defined D_{∥, eff}′ = D_∥′ + DJ′/2J. Following previous work¹⁹, we also include a hopping between next-neighbour dimers, corresponding to a further-neighbour Heisenberg exchange J_FN. This coupling enters into the diagonal elements as .

The qualitative effects of each exchange term on the dispersion are as follows. The J term simply gives a gap to the triplons. The inter-dimer DM couplings break the degeneracy of the triplon bands over most of the Brillouin zone. They leave the central mode dispersionless and the dispersion of the upper and lower bands symmetrical about the middle band so that the energies do not change under sign flips of the DM couplings. The D_{∥, eff}′ coupling leads to linear touching at the Brillouin centre and corners. D_⊥′ leads to quadratic touching at the Brillouin zone corners. In order to break the symmetry between the upper and lower bands, and to introduce a dispersion for the central mode, we introduce J_FN. The modes measured in SrCu₂(BO₃)₂ appear to be asymmetrical in the above sense.

The intra-dimer anisotropic exchange J_zz breaks any degeneracy between one pair of modes and the other two pairs. The intra-dimer coupling J_xy completely lifts the degeneracy of the modes except at the Brillouin zone corners. This implies that there can be no transformation that allows one to render sublattices A and B equivalent.

Note that anomalous quadratic terms t_Aα^†t_Bβ^† and t_Aαt_Bβ arise from the bond-operator representation of the coupling between spins of neighbouring dimers. These terms have a negligible effect on the triplon dispersion of the order of D′/J ≃ 3% relative to the triplon bandwidth W ∼ D′ (Supplementary Information).

Singlet bound state.

We consider two-triplon bound states as candidates for the new dispersing feature in the neutron-scattering data. We expect the lowest energy bound state to belong to the total S = 0 sector with wavefunction

In general, the bound state will have four modes corresponding to the four choices of sublattice pairs. The bound state can be captured within a perturbative calculation even to low order, as the J′ term induces a correlated hopping of neighbouring triplons which lowers the energy relative to the two-triplon continuum. To see this, we consider two sets of four states (see Supplementary Information), denoted by sectors I and II, respectively. In momentum space, we define the bound-state creation and annihilation operators by

with similar definitions for two-triplon states in sector II. The spectra for the bound states for sector I to third order in perturbation theory are found by diagonalizing the matrix²⁰

where the potentials and hopping terms are

For sector II, the Hamiltonian is given by H_Bound^(S−II) = H_Bound^(S−I)(k_y → −k_y), so the dispersion for sector II is related to that for sector I by a reflection about k_x = 0. Since J′/J ≈ 0.6 (ref. 26) is not small, the perturbative expansion might not be very well controlled. We therefore allow the parameters V_NN, V_NNN, J_NN and J_3rd that enter the above 4 × 4 matrices to be independent. At k = 0, the ground states of the two-triplon sectors are degenerate. This degeneracy is accidental and lifted by terms that are fourth order in J′/J and couple the two-triplon bound states of the two sectors. We also include such terms which are perturbatively equal to K = 3J⁴/(32J³).

Hybridization.

The DM interactions supply a means for the singlet bound states and single-triplon modes to hybridize. The three-body triplon Hamiltonian arising from J′ (equation (4)) directly couples the two. A second contribution arises from equation (5) after performing the transformations equations (2) and (3) on a single-triplon operator. This contribution merely renormalizes the first. The hybridization matrix between the six single-triplon states and the four two-triplon singlet states in sector I is

where the six single-triplon states are organized as described above. As before, we have absorbed the shift of the coupling constants, D_{∥, eff}′ = D_∥′ + DJ′/2J and D_{s, eff}′ = D_s′ − DJ′/2J (arising from the diagonalization of the local dimer Hamiltonian) in a re-definition of parameters. For sector II, we find

Dynamical structure factor.

The INS intensity is

for scattering wavevector K and energy loss ω. The copper Cu²⁺ form factor is F(K) and P_αβ(K) is the transverse projector . The spin operator here is

where R_i labels the primitive tetragonal lattice vectors and r_A1 and so on label the basis. We introduce the bond-operator representation and carry out the unitary rotation of the singlet and triplet operators necessitated by the presence of the intra-dimer DM interaction. After acting on the vacuum the result is

where h = (4z − 1)/2 is the distance along the c direction between dimers nominally in the same layer. Finally, we transform the triplon operators into the basis {|n〉} of eigenmodes to calculate the matrix elements entering equation (7).

Fitting procedure and parameters.

Our fitting procedure is as follows. We take various cuts at constant momentum through the data at zero field and fit the peaks to Gaussians with variable mean and variance, taking the minimal number of Gaussians necessary to obtain a good fit to each cut. In this way we obtain a set of points tracking the dispersion curves of the triplon modes. To these points, we fit the free-triplon model using a least squares minimization algorithm and obtain a set of exchange parameters. The quality of the fit suggests that the model includes all necessary exchange couplings, which we refine below in the presence of the bound state. The parameters are weakly correlated. For example, J sets the 3 meV gap, the DM couplings have quite different effects on the dispersion, the further-neighbour hopping term breaks the reflection symmetry about the central triplon mode and the J_zz and J_xy anisotropies break the zero field degeneracy at the M point in different ways. Energy cuts at constant |Q| indicate some degeneracy breaking at the M point at zero field, and hence that J_zz or J_xy or both are non-negligible.

To fit the full model, we choose random initial parameters and fit first the decoupled bound-state parameters and the decoupled single-triplon parameters using a least squares procedure. We then switch on a fixed set of hybridization parameters and relax all the parameters to an optimal fit. The entire procedure is automated, apart from the choice of hybridization parameters, which were tuned manually to obtain a good fit.

The best-fit parameters for the full model include the parameters entering the free-triplon Hamiltonian H₂ which are given in the main text. The effective parameters entering the 4 × 4 matrices of the closed sectors of two-triplon singlet states are given by Δ = 2.342 ± 0.02 meV, J_NN = −0.25 ± 0.02 meV, V_NN = −0.346 ± 0.03 meV, V_NNN = −0.362 ± 0.02 meV, J_3rd = −0.25 ± 0.05 meV.

For the coupling between the two two-triplon sectors we find K = −0.2056 ± 0.004 meV. The hybridization parameters between the triplons and the two-triplon singlet states are  meV,  meV, and  meV. Note that we have allowed the hybridization parameters to be different from the DM couplings entering H₂.

To determine the errors on these parameters, we created multiple data sets—each one being the original dispersion picks plus some Gaussian noise, with the width being set by the experimental broadening. We optimized the parameters for each of these data sets, thus obtaining a measure of the distribution of fitting parameters over this noisy data. The quoted errors are the estimated widths for the calculated distribution of each parameter.

Berry curvature and Chern numbers.

The Berry curvature of a band in a crystalline medium is a fictitious local magnetic field that depends on the Bloch wavefunction |ψ⁽ⁿ⁾(k)〉 of the band. The analogue vector potential or Berry connection is A_μ⁽ⁿ⁾(k) = 〈ψ⁽ⁿ⁾(k)| ∂_μ |ψ⁽ⁿ⁾(k)〉, from which the Berry curvature may be found from F_μν⁽ⁿ⁾ = ∂_μA_ν⁽ⁿ⁾ − ∂_νA_μ⁽ⁿ⁾—the derivatives being taken in crystal momentum space. We computed the Berry curvature using the link variable method of ref. 34. The integral of the Berry curvature F_xy over a two-dimensional Brillouin zone is an integer topological invariant—the first Chern number—which simply measures the number of times the mapping F from the Brillouin zone torus covers a torus

The sum of Chern numbers of all bands is zero and C_n itself is zero unless time reversal H(k) = H^∗(−k) is broken. This invariant is well defined only when the band index is well defined, so the bands should not have touching points. Such touching points exist in our model at the corner of the Brillouin zone, irrespective of the field B perpendicular to the plane. In the calculation we include a small transverse field component to lift this degeneracy. It is well known that, when a pair of bands do touch and separate, the net Chern number of the pair remains unchanged. Since the total Chern number of the pair turns out to be non-zero, the topology remains protected even in the limit of zero transverse field.

Edge states.

Implementing the Hamiltonian with triplon modes and both bound-state sectors (14 bulk modes) on an infinite strip which is 20 lattice sides wide, gives rise to a 280 by 280 coupling matrix with energy eigenvalues ε_i(k_x). To identify edge states, for each eigenvalue ε_i(k_x) we compute the overlap of the corresponding eigenstate with all single-triplon and two-triplon singlet states on a given layer j. From the resulting probability distribution $P_{i,k_x}$(j) we can easily identify edge states from the condition that the mean ${〈j〉}_{i,k_x}$ of the distribution lies within the top (blue) or bottom (red) two layers of the strip.

Data availability.

Raw data for this manuscript is available at https://doi.org/10.5286/ISIS.E.74043138 and https://doi.org/10.5286/ISIS.E.74043168.