Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
1K views

IB Math SL 2 - Integration Worksheet Name - 1

This document contains 10 math integration problems. Problem 1 involves finding the derivative and integral of a function defined by its minimum point, sketching its graph, and evaluating it at several points. Problems 2-7 contain various integration problems involving trigonometric, exponential, and other functions. Problems 8-9 involve taking derivatives and integrals of given functions, and calculating other related values. Problem 10 has 4 integration problems to find the exact value of.

Uploaded by

glennbondoc
Copyright
© © All Rights Reserved
Available Formats
Download as DOC, PDF, TXT or read online on Scribd
1K views

IB Math SL 2 - Integration Worksheet Name - 1

This document contains 10 math integration problems. Problem 1 involves finding the derivative and integral of a function defined by its minimum point, sketching its graph, and evaluating it at several points. Problems 2-7 contain various integration problems involving trigonometric, exponential, and other functions. Problems 8-9 involve taking derivatives and integrals of given functions, and calculating other related values. Problem 10 has 4 integration problems to find the exact value of.

Uploaded by

glennbondoc
Copyright
© © All Rights Reserved
Available Formats
Download as DOC, PDF, TXT or read online on Scribd
You are on page 1/ 2

IB Math SL 2 Integration Worksheet

1.

Name_______________

The function f is such that f (x) = 2x 2.


When the graph of f is drawn, it has a minimum point at (3, 7).
i) Find f (x)

(a)

ii) Hence find f(x).


(6)

(b)

Find f (0), f (1) and f (1).


(3)

(c)

Hence sketch the graph of f labelling it with the information obtained in part (b).
(4)

(Note: It is not necessary to find the coordinates of the points where the graph cuts the x-axis.)
(Total 13 marks)

2.

3.

Find

sin (3x 7) dx;

(a)

Let f(t) =

t3

4.

5.

6.

Let f(x) =

1
5
2t 3

. Find

(b)

4 x

dx .

f (t ) dt.

(Total 3 marks)

x 3 . Find

(a)

f (x);

(a)

Find

(b)

Given that

f ( x)dx.

(b)

(Total 6 marks)

dx
, giving your answer in terms of m.
2x 3

m
0

m
0

dx
= 1, calculate the value of m.
2x 3

The derivative of the function f is given by f (x) = e

2x

Let f be a function such that


(a)

3
0

(Total 6 marks)

f ( x ) dx 8 .

Deduce the value of


(i)

(b)

(Total 6 marks)

1
, x < 1.
1 x

The graph of y = f(x) passes through the point (0, 4). Find an expression for f(x).

7.

(Total 4 marks)

d
c

3
0

2 f ( x ) dx ;

(ii)

f ( x) 2 dx .
0

f ( x 2)dx 8 , write down the value of c and of d.

(Total 6 marks)
1

8.

9.

The function f is given by f(x) = 2sin(5x 3).


(a)

Find f "(x).

(b)

Write down

f ( x)dx .

(Total 6 marks)

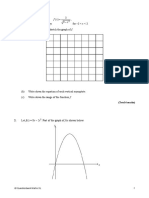
The table below shows some values of two functions, f and g, and of their derivatives f and g .
x

f(x)

g(x)

f (x)

g (x)

Calculate the following.


(a)

d
(f(x) + g(x)), when x = 4;
dx

(b)

g' ( x) 6 dx .

(Total 6 marks)

10. Find the exact value of the following:

(4 marks each)

(a)

4 x 3 dx

1
4

(b)

3
dx
6 x 2

(c)

(d)

8
dx
5 x 6

4sin 2 x

1
dx
cos 2 x
(Total 16 marks)

Verify the above answers using your GDCs

You might also like